基于货物时间价值的中欧班列服务网络设计
2020-07-13魏玉光凌铭君
张 琦,姜 昊,2,魏玉光,凌铭君,杨 浩
(1.北京交通大学 交通运输学院,北京 100044;2.中国铁路济南局集团有限公司 淄博车务段,山东 淄博 250000)
随着“一带一路”倡议深入施行,中欧班列逐步发展成为亚欧大陆上国际铁路运输通道的重要载体。然而,部分班列线路始发城市相近、终到城市相同、运输路径重叠,现有班列线路存在同质化竞争问题,同时因班列运输需求有限,供需失衡,同质化竞争更加激烈,影响中欧班列的可持续发展。
针对此问题,既有的中欧班列相关文献以定性研究为主,定量研究普遍聚焦枢纽选址[1-2]、线路选择[3-4]、开行方案[5-6]等,通常忽视货物时间价值特性以及运输时效性需求的差异化。因此亟须构建与货物时间价值特性相符的经济高效的中欧班列服务网络[7]。运输服务网络设计问题衍生自网络设计理论在运输领域的应用以及运输网络的抽象化[8-9],目前已有诸多学者对铁路运输服务网络设计进行研究[10-11],解决运输组织优化[12]以及运输路径优化[13]等问题。
中欧班列服务网络设计旨在遵循 “干支结合”的班列组织原则,即在尽量维持中欧“直达班列”的常态化运营的同时,增设适量的“中转班列”,在条件允许的情况下合并低效、重复的“直达班列”,优化货源组织效率,降低班列服务网络的综合成本。本文针对中欧班列运输路径重叠问题,考虑货物时间价值特性以及运输时效性的需求,以综合运输成本最小化为目标,研究与货物时间价值特性相符的中欧班列服务网络。
1 货物时间价值计算方法
本文引入货物时间价值理论,用以计算中欧班列服务网络的时间成本,同时设置费用和时间各自的权重系数,以两者加权合并得到的“综合运输成本”,实现运输经济性和时效性的归纳统一。
综合运输成本C为
C=θ1Cv+θ2Ct
(1)
Ct=βtq
(2)
θ1+θ2=1
(3)
式中:θ1为运输费用权重系数;θ2为时间价值权重系数;Cv为运输费用,元;Ct为时间价值,元;β为单位时间价值,元/(d·TEU);t为运输时间,d;q为货物运量,TEU。

图2 中欧班列服务网络
本文对货物时间价值的定义为:货物在运输途中因贬值或资金占用而产生的货币损失或客户为节约运输时间而额外支付的费用。本文综合考虑货物运输途中对资金的占用、货物自身损耗或折旧成本以及货物因时间延误产生的贬值等因素,计算单位时间价值β。此外,考虑到货物自然性质的差异性,设置货物性质系数λ对β进行修正,从而引入货物自然性质对时间价值的影响。根据文献[14-15],β为
(4)
式中:W为货物价值,元/TEU,可用货物的市场价格反映;S为社会折现率,可选择年贷款利率进行赋值。
本文基于客户调查,利用层次分析法确定运输费用权重系数θ1和时间价值权重系数θ2。
2 中欧班列服务网络设计模型
2.1 中欧班列服务网络的概念及表示方法
中欧班列货运网络包括物理网络与服务网络双层维度。物理网络由中欧班列始发城市、终到城市的铁路货运站及编组站、节点间铁路线路及其衔接关系组成,服务网络则是建立在物理网络基础上,基于运输需求,由运输企业在中欧班列城市节点间提供各种运输服务构成的虚拟网络。不同于物理网络,中欧班列服务网络主要针对货物运输需求配置安排载运设备,实质上表现为运输企业对运输资源的合理配置和利用。
中欧班列服务网络需要能够反映班列始发城市、终到城市间直达班列与中转班列的配置情况,因此本文在服务网络中设置到发节点、需求节点、服务弧段。到发节点由物理节点拆分得到,一个物理节点可拆分为若干到发节点,用以判断物理节点间能否通过某一运输服务进行联通。需求节点和到发节点统称服务节点,服务节点间又由运输服务相连,构成服务弧段,由此便能同时反映运输需求从产生至满足的完整过程,包括中欧班列的在途运输过程及相关各项作业过程,物理节点内部服务弧段的运输服务的费用及时间属性实质表示作业费用及时间。以图1所示的简单中欧班列物理网络为例,假设班列始发城市A、B、C均能够独立运营终到城市为D的直达班列,同时城市A可作为中转城市,集聚城市B、C的货源并开行中转班列,则其对应的中欧班列服务网络见图2。
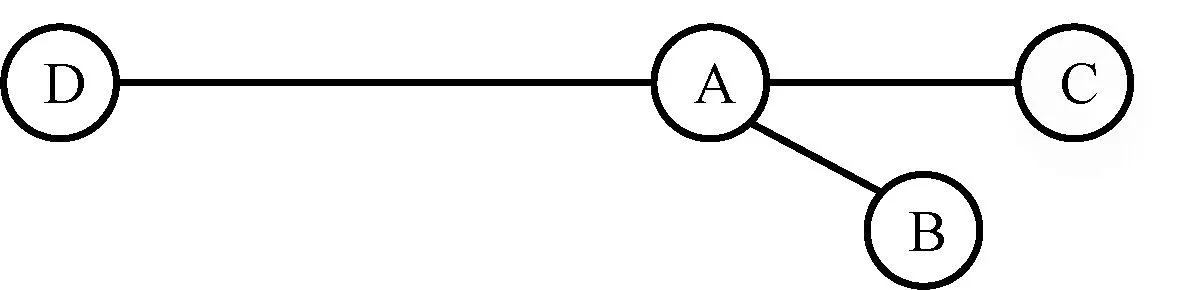
图1 中欧班列物理网络
2.2 基本假设
为方便模型建立以及对模型实际情况的反映,模型的基本假设如下:
(1)设定决策周期为一周,且决策周期内运输需求规模及分布已知,客户均为“理性经济人”。
(2)不考虑政府补贴对中欧班列上层服务网络设计的影响。
(3)不考虑始发城市作业能力的限制。中转城市从始发城市中选择,且数量为1。
(4)不考虑班列始发、终到作业时间和费用对服务网络设计的影响。
2.3 参数设置
I为始发城市集合,i∈I;J为中转城市备选集合,j∈J;N为服务节点集合,m,n∈N;nij为物理节点i内j方向的到发节点;F为服务弧段集合,a,b∈F;qi为始发城市i运输需求规模,TEU;li为始发城市i开行的直达班列数量,列;ω(l)为班列运载能力,TEU/列;xij为决策变量,表示始发城市i至中转城市j的中转货流量,TEU;yj为0-1决策变量,yj=1表示城市j从集合J中被选中,否则为0;σ(i,j)为辅助变量,xij>0时,σ(i,j)=1;S取4.35%;ni为始发城市i的需求节点;ns为终到城市s的需求节点。

2.4 中欧班列服务网络设计模型
由于直达班列、中转班列涉及运输或作业过程较多,在不失一般性的基础上,仅在目标函数中保留中转班列相关成本参数,将直达班列相关成本参数用于构建约束条件加入模型。以服务网络综合运输成本最小化为优化目标,模型为
(5)
s.t.
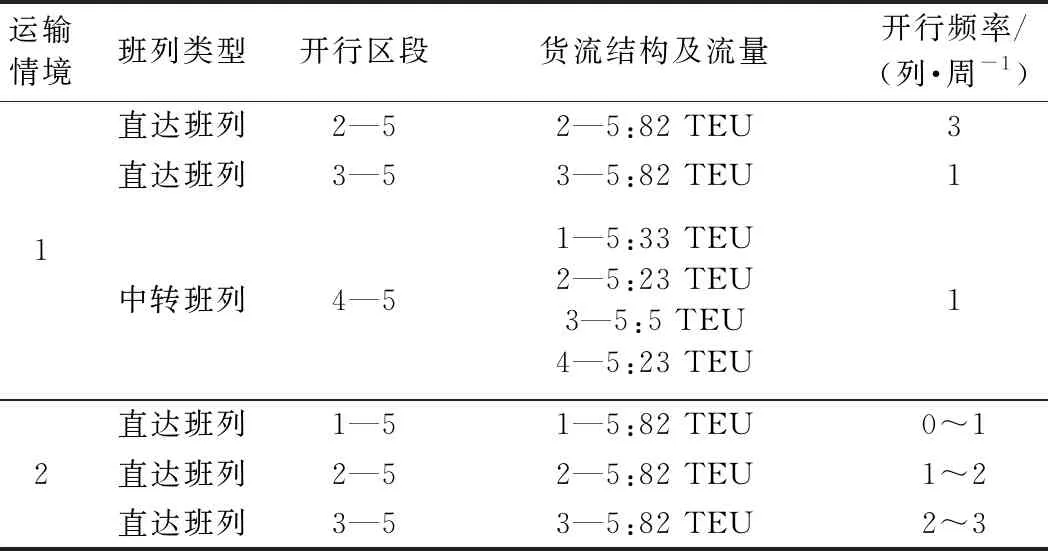
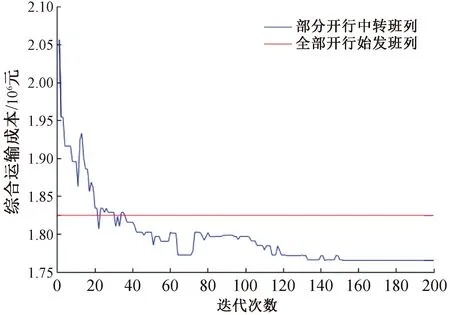
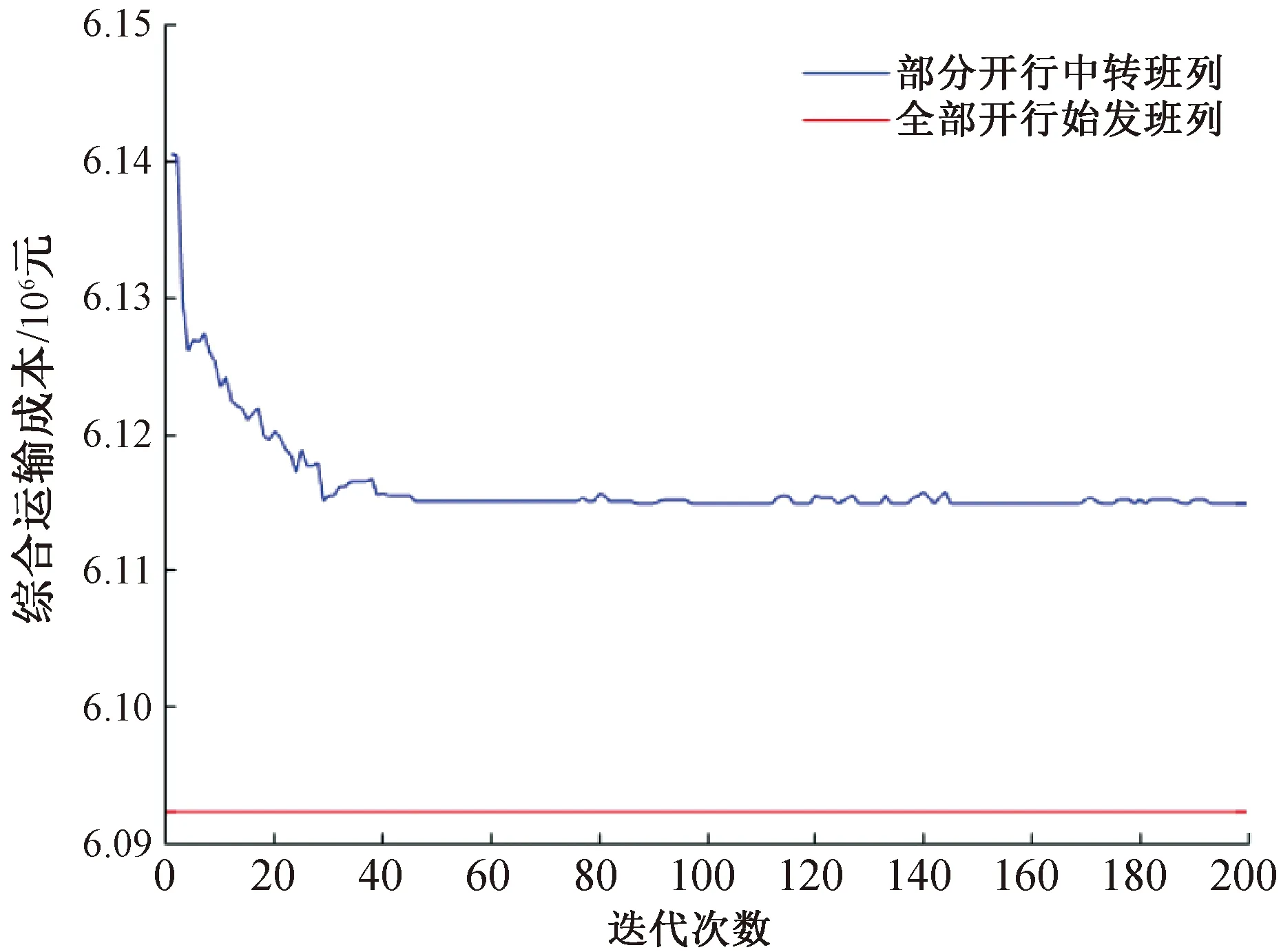
σ(i,j) (6) σ(i,j)≤tmax (7) xij<ω(l) (8) (9) (10) σ(i,j)∈{0,1}yj∈{0,1} (11) 式(6)表示若货物选择由中转班列进行运输,则中转班列的综合运输成本应小于直达班列的综合运输成本。式(7)表示若货物选择由中转班列进行运输,则中转班列的货源集疏运、货物中转、集结等待及在途运输过程的运输时间及作业时间不超过运到期限。式(8)表示始发城市中转至中转城市的货物流量不能保障班列满轴开行。式(9)表示所有始发城市中转至中转城市的货物流量能够保障班列满轴开行。式(10)表示选择且仅选择1个始发城市作为中转城市。式(11)为逻辑约束,用以保证模型的参数取值与逻辑正确。 中欧班列服务网络中始发城市数量众多,模型解的规模庞大,采用精确算法求解困难,而遗传算法在求解运输问题上的优越性明显,染色体编码机制灵活,能够保证解的多样性,因此本文采用遗传算法求解模型。 图3 染色体编码策略示意 因模型目标为中欧班列服务网络综合运输成本最小,因此以综合运输成本的倒数为适应度函数,从而完成转化,即综合运输成本越小,适应度值越大,染色体的解越优,即 (12) 因本文采用混合进制编码,在染色体交叉操作过程中需避免不同基因间的交叉,因此需先确定交叉区域,在各自的交叉区域完成交叉操作,见图4。 同理,本文采用动态进制变异策略,利用随机数r2∈[0,1]决定染色体变异的基因位置。若r2∈[0,0.5],则染色体遵循动态进制变异规则,在第1至|I|位随机选择基因变异;若r2∈(0.5,1],则染色体遵循2进制变异规则,在第|I|+1至2|I|位随机选择基因变异,见图5。 图5 染色体变异策略示意图 本文遗传算法的基本流程为: Step2进行染色体编码、染色体基因检验与修正,随后产生初始种群,规模为Psize。 Step3计算所有染色体的适应度,并更新遗传代数,Gc=Gc+1,判断是否达到最大遗传代数Gmax,若是,转至Step6;否则转至Step4。 Step4基于染色体的适应度值,采用“轮盘赌法”从第Gc代父代种群中选择种群规模为Psize的繁衍种群。 Step5对繁衍种群中的父代染色体进行交叉和变异操作,生成子代种群,转至Step3。 Step6输出适应度最强的染色体并解码,得到中欧班列服务网络设计最优方案。 本文选择开行大量中欧班列的西通道为例,重庆、西安与德国杜伊斯堡间拥有常态化运营的直达班列,成都、乌鲁木齐曾开行至杜伊斯堡的直达班列,但班列开行频率相对较低。上述4个始发城市的直达班列终到城市相同,运输路径重叠,且部分始发城市距离相近,直达班列具有相似性与可替代性,符合本文所研究问题的特点。因此,本文选择成都、重庆、西安、乌鲁木齐作为始发城市,德国杜伊斯堡作为终到城市。通过设置不同运输情境,研究中欧班列服务网络设计问题。 根据实际调研与既有研究,重庆、成都、西安、乌鲁木齐及杜伊斯堡间的运输距离见图6。 重庆重庆成都337成都西安716842西安乌鲁木齐2 7733 0262 433乌鲁木齐杜伊斯堡11 17911 41210 8398 406 图6 运输距离矩阵(单位:km) 本文基于对重庆、成都、西安、乌鲁木齐的中欧班列的开行频率和货源结构的统计分析,根据货物时间价值理论,将中欧班列货物可分为高价值时间敏感性货物、低价值时间敏感性货物、高价值时间不敏感货物、低价值时间不敏感货物4类,参考实际调研与既有研究[7-8],确定该4类货物的权重系数见表1。但因篇幅有限,将4类货物简化为时间敏感性货物和费用敏感性货物2类,分别针对时间敏感性货物、费用敏感性货物设置2种不同运输情境进行对比,相关参数见表2。 表1 不同类型货物的权重系数 服务弧段的费用属性包括运输费用与作业费用,服务弧段的时间属性包括运输时间与作业时间。根据实际调研,中欧班列服务网络内服务弧段的运输、作业费用与运输、作业时间包括但不限于表3所示各项。 表 2 不同运输情境下的参数设置 表 3 服务弧段的费用及时间标准设置 将成都、重庆、西安、乌鲁木齐及杜伊斯堡的序号分别设为1、2、3、4、5;将算例数据输入遗传算法,求解得到中欧班列服务网络设计结果,如图7、图8及表4所示。情境1中班列的优化方案合并了部分低效、重复的“直达班列”,从而缓和了中欧班列的同质化竞争问题。 图7 情境1中欧班列服务网络设计结果 图8 情境2中欧班列服务网络设计结果 情境1、2的算法迭代过程分别见图9、图10。 研究结果表明,中转班列的开行受到货源分布及规模、货源集疏运速度、货物运输需求特性等多种因素的影响。其中货源分布离散、集疏运速度较慢的时间敏感性货物通常能够支持中转班列的开行。因此,情境1中,通过缩减时间敏感性货物的集结等待时间,产 表 4 中欧班列运输服务配置情况 图9 情境1算法迭代过程 图10 情境2算法迭代过程 生的货物时间价值能够弥补中转过程产生的额外费用,降低综合运输成本,中转班列的开行具备技术可行性与经济可行性。情境2中,费用敏感性货物对时效性需求较弱,缩短集结等待时间并不能降低综合运输成本,中转班列的开行具备技术可行性但不具备经济可行性。此外,中转城市的地理位置应尽可能便于其他城市进行铁路运输,同时避免迂回、对流运输等不合理运输问题造成的运输费用增加与运输资源浪费,因此,在情境1中,乌鲁木齐更适于作为中转城市。 本文提出中欧班列服务网络概念,以综合运输成本最小化为目标构建得到中欧班列服务网络设计模型,并设计遗传算法实现模型的求解。研究结果表明,适当开行中转班列,合并低效的同质化班列线路,能够缓解中欧班列线路间的恶性竞争,符合《中欧班列建设发展规划(2016—2020)》中“干支结合”的班列组织原则。同时,通过缩减时间敏感性货物的集结等待时间,产生货物时间价值,降低中欧班列服务网络的综合运输成本。3 遗传算法设计
3.1 遗传算法核心步骤

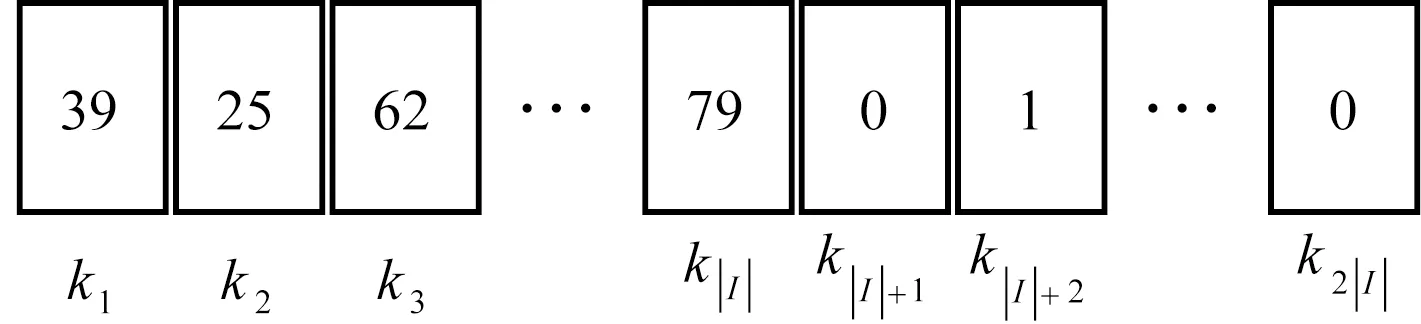
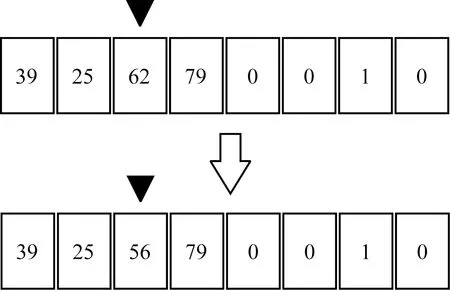
3.2 遗传算法基本流程

4 算例分析
4.1 算例背景
4.2 算例数据




4.3 算例求解
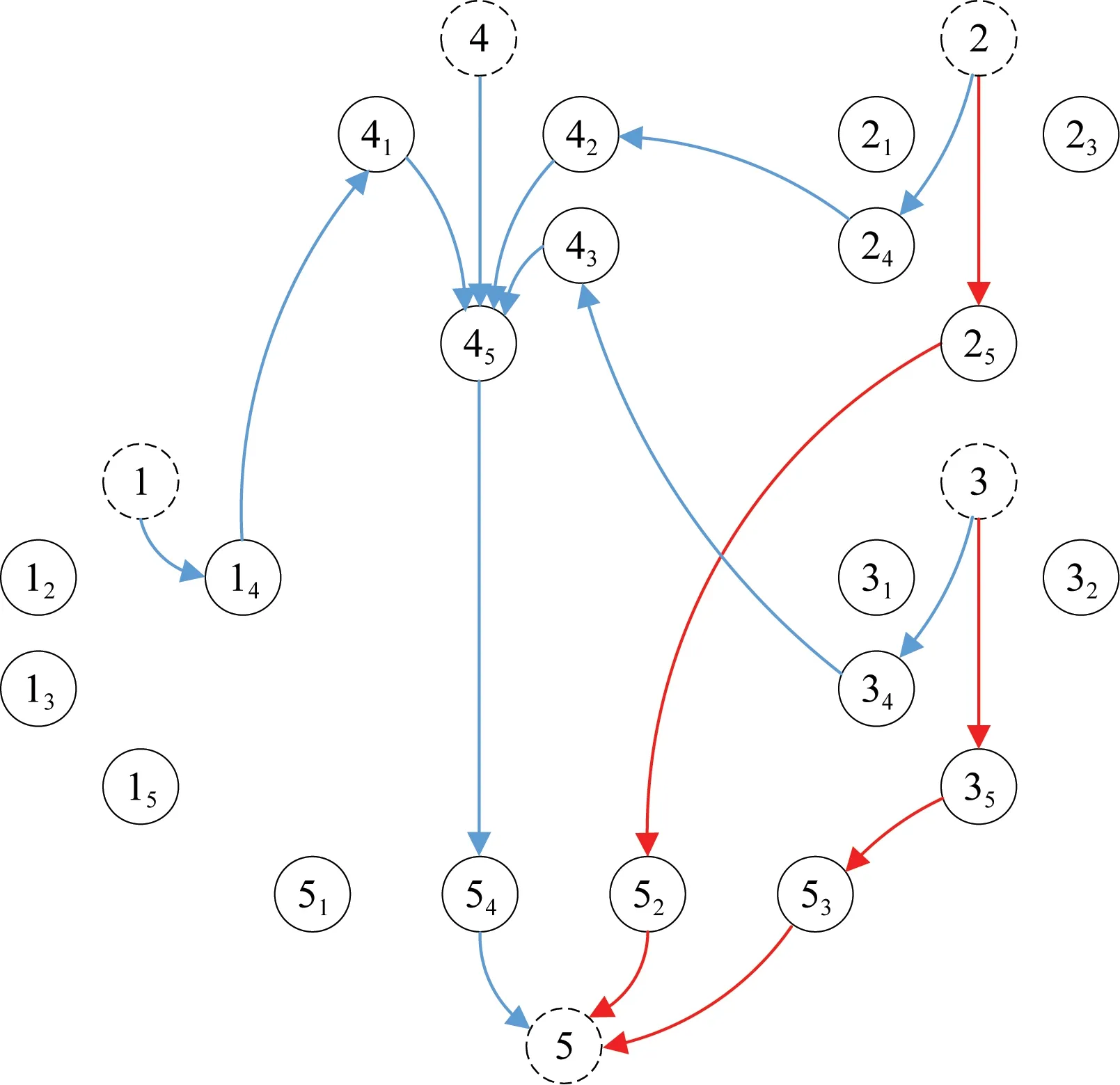

5 结论
