自适应截断奇异值结合有效集的T2谱反演方法

李鹏举， 王梓丞， 任 莉

(1.东北石油大学 地球科学学院， 黑龙江 大庆163318； 2.东北石油大学 非常规油气成藏与开发省部共建国家重点实验室培育基地， 黑龙江 大庆163318； 3.中国石油集团测井有限公司大庆分公司解释评价中心， 黑龙江 大庆163000)

0 引 言

核磁共振测井技术能够提供地层岩石物理性质和流体性质参数，如孔隙度、渗透率、可动水饱和度等[1,2]。这些参数能否计算准确与T2解谱技术息息相关。解谱技术是核磁共振测井技术的关键。目前，广泛使用的解谱技术的实质是多指数反演，反演方法有奇异值分解(SVD)[1,3-5]和最优化及其改进方法[6]。例如：肖立志等[1,5]基于奇异值分解的反演方法；王为民等[7]提出基于解的自由度选取最优反演模型的反演变换法；K.J.Kunn等[8]，王才志等[9]采用奇异值分解与正则化方法结合截去小的非零奇异值的方法。学者们普遍采用截断法或正则化方法确保解的稳定与平滑。截断奇异值的选择和正则化因子的选取与噪声有关，一般采用信噪比作为噪声的统计特征参数。而CPMG回波信号为多指数衰减信号，与稳恒信号不同，信噪比并不是常数[3]。因此，以信噪比作为衰减信号的统计特征参数不适合。以噪声的方差作为噪声的统计特征参数，来确定截止奇异值，能够最大限度提取自旋回波中的有用信息。根据解的物理意义，T2谱的幅值应为非负实数。为了保证解的非负性，广泛采用改进迭代法随机搜索非负解，而这种解法可能会丧失解的连续性[4,10]。产生这个问题的原因是方程的求解与非负约束相分离。为此，笔者结合奇异值分解和最优化方法，在保证解的稳定性的同时进行非负约束，避开对解的随机迭代搜索，以有限的计算次数快速求解连续的T2谱。

1 T2谱反演方法

1.1 储层孔隙流体弛豫模型

岩石的孔隙度由岩石的矿物组分、孔隙中黏土分布与孔隙结构等因素共同决定。核磁共振测井方法能够提供岩石中各种流体的信息以及渗透率信息，并且不受岩性影响。测井仪器以氢核为目标采集包含孔隙流体信息的自旋回波串，通过自旋回波法得到横向弛豫时间常数[1-2,11]，即

(1)

式中：bi——回波幅度序列；

fi——第i个分量初始幅度；

ti——采样时间；

T2j——第j个横向弛豫时间常数；

n——回波个数；

m——横向弛豫分量个数；

εi——噪声序列[4]。

将式(1)写成矩阵形式，即

b=Af，

(2)

其中，b=g+ε；g∈Rn；b∈Rn；A∈Rn×m；f∈Rm；ε∈Rn。

由初始幅度f预设多个横向弛豫时间常数拟合多指数衰减序列b的过程称为T2谱反演。

1.2 固定截断奇异值法

式(2)不存在唯一解，无法进行工程应用，为得到最合适的最小二乘解，由式(2)得

f=A+b，

(3)

式中，A+——矩阵A的伪逆矩阵。

将矩阵A+奇异值分解代入式(3)，得

(4)

其中，r=rank(A)，Ur∈Rn×r，Vr∈Rm×r。

由于式(4)中奇异值由大到小排列，将小于预设截断值δk的项全部取零值得

(5)

式中：δ1——最大奇异值；

δk——截断奇异值；

g——无噪声信号；

ε——噪声信号。

在此步骤中难点在于截断值的选取工作，若截断奇异值δk选取偏大会导致结果误差变大，降低准确性；相反则导致解的稳定性变差。适当的截断值必须平衡解的稳定性与结果的平方误差两方面影响。

1.3 自适应截断奇异值法

传统截断奇异值方法衡量噪声统计特征时，以信噪比作为参数[1-2]，并以信噪比作为截断奇异值选取依据。然而，回波序列是一种不同于稳恒信号的多指数衰减信号，在噪声环境不变的情况下，信噪比是随时间变化的变量。在实际处理过程中影响信噪比的因素很多，单纯以信噪比作为截断奇异值选取依据，无法保证解的稳定性和一致性。本文提出的方法在衡量噪声统计特征时，以噪声的方差作为参数衡量噪声幅度。由式(5)得：

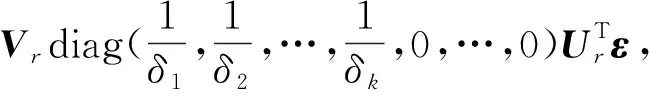
(6)

式中：fs——有用信号项；

fn——噪声项。

引入参数T2snr，有

(7)

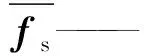
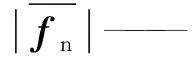
利用T2snr评价解的准确性，T2snr值与解的准确性呈正相关关系，与解的稳定性呈负相关。利用自适应搜索法自动选取奇异值截断值，平衡解的稳定性与准确性相矛盾现象。

首先对经过奇异值分解得到的对角阵中奇异值最大值进行搜索，判断由经验选取的目标函数M是否小于T2snr。若不满足，计算下一个奇异值；若满足，则停止搜索，并以上一个奇异值为奇异值截断值。自适应搜索法具体流程图如图1所示，步骤如下：

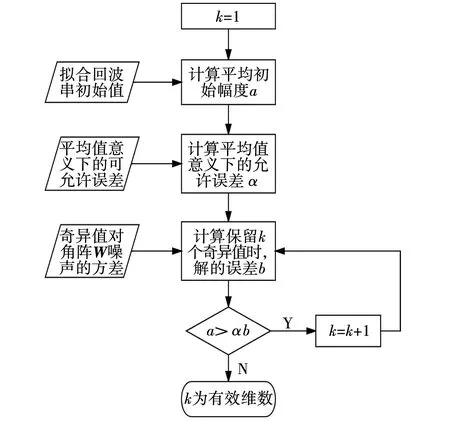
图1 自适应搜索流程Fig. 1 Adaptive search flow

步骤一以对角阵中奇异值最大值δ1作为搜索初始值，即令k=1。

步骤二以第k个奇异值作为奇异值截断值进行反演计算，得到f。

步骤三计算fs和|fn|。根据研究可知，反演结果中噪声项均值为零，因此，fs=f。随机信号ε的方差由正交方程组性质得：

(8)

式中,Vi、Ui——标准正交向量组。

噪声项的方差为

(9)

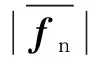
步骤五令k=k+1，执行步骤二。

步骤六以δk-1作为奇异值截断值输出。

1.4 有效集非负约束法

在井下核磁仪器采集信号过程中，难免会记录无用信号，例如噪声。在解谱过程中由于无用信号的存在，反演结果无法准确反映井下真实流体信息，尤其是解出现负值的情况，不符合实际物理意义。传统的非负约束方法，例如迭代法非负约束等均采用迭代的方法去除负解，其缺点有：迭代次数较多时，计算速度较慢；迭代次数较少时约束效果较差。采用有效集最小二乘非负约束方法可保证解的非负性。

根据最优化理论的思想结合T2谱反演构造目标函数，以解的非负性作为约束条件，得

(10)

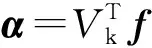
(11)

由二次规划一般形式得

此外，我国养老服务还存在发展不平衡问题，居家社区与机构养老服务发展不均衡，城乡养老服务业发展不平衡，区域间养老服务业发展不平衡。公办机构建设水平总体好于民办机构，城市养老机构明显高于农村敬老院的保障水平。

(12)

式中,H——n阶对角阵。

有效集最小二乘非负约束方法获取最优解α具体流程如图2所示，步骤如下：

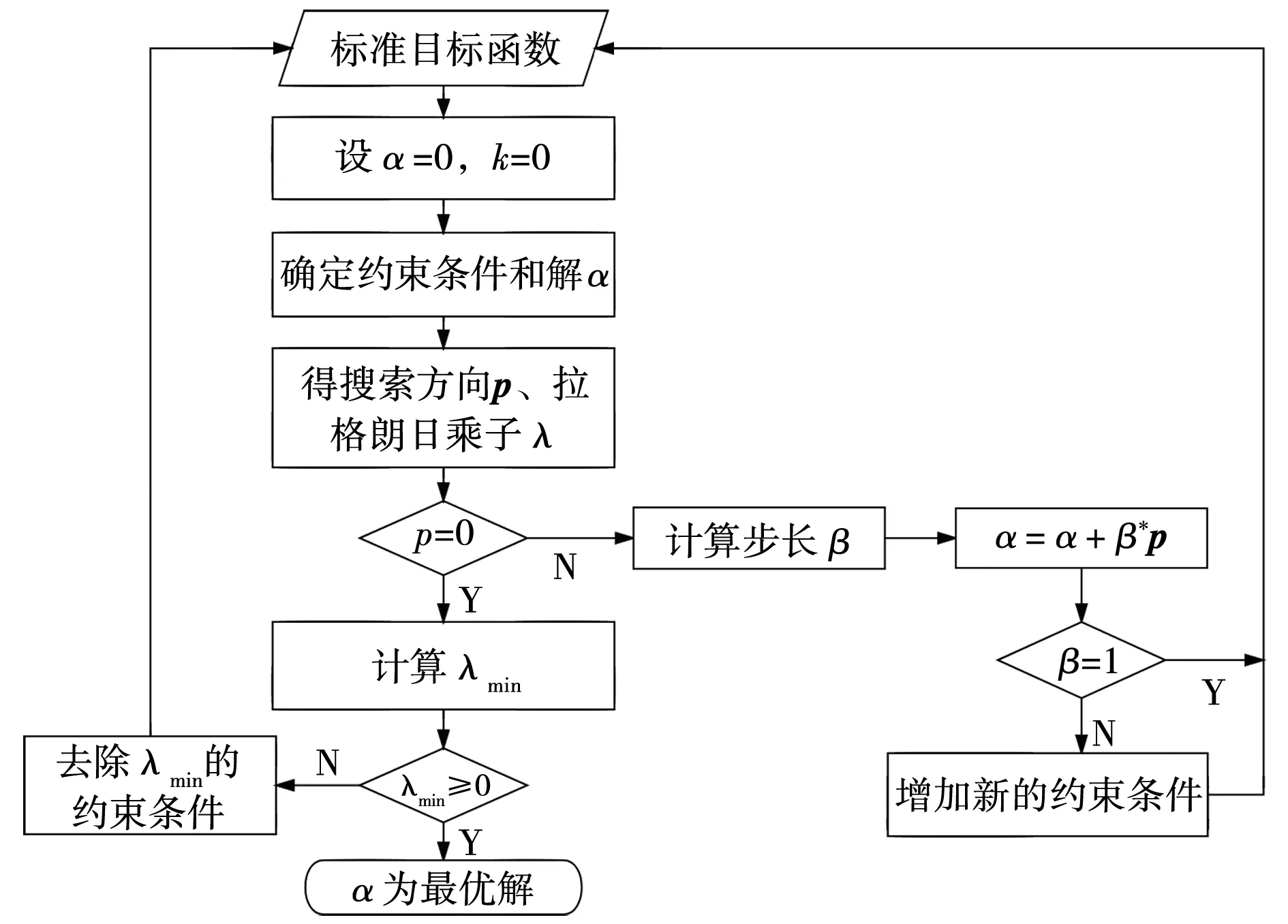
图2 有效集非负约束流程Fig. 2 Active set non-negativity constraint flow

步骤一确定初始值。以可行点αk(k=0)为起点。

步骤二求解子问题。确定有效约束的等式条件，得

(13)

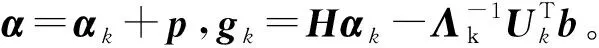
步骤三终止准则的检验。引入新的参数λk，即拉格朗日乘子，表达式为

λk=Bkrk，

(14)

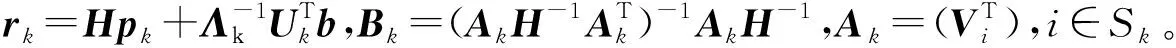
令(λk)t=min{(λk)i}，i∈I(αk)。若(λk)t≥0，终止运算，并以αk为结果输出；若(λk)t<0，则将有效集中第t个约束条件去除，令Sk=Sk/{t}，执行步骤二。

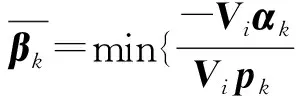
步骤五令k=k+1，执行步骤二。

2 仿真实验

为了检验方法的有效性，参考实际地质状况，运用数值模拟技术构造T2谱得到构造谱，参照P型核磁系统，按照式(1)正演出不同信噪比的回波数据。对这些数据做T2谱反演，与构造谱对比，研究方法的有效性。

2.1 不同截断奇异值方法的对比

正演过程中，分别给回波信号加入信噪比αSNR分别为10、50、200、105的高斯噪声，分别用自适应截断奇异值和固定截断奇异值方法进行反演，固定截断奇异值δ分别为1.389 2、0.313 1、0.064 7，如图3所示。

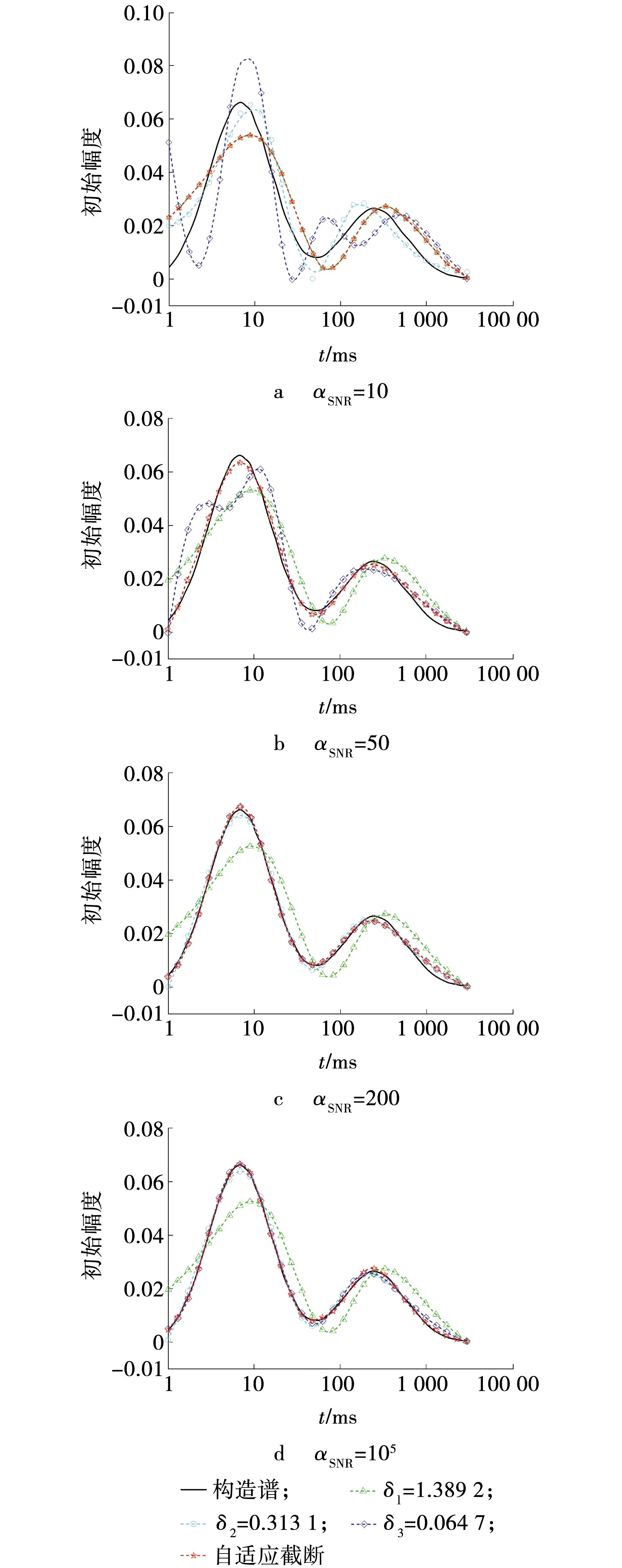
图3 不同信噪比下T2谱反演结果Fig. 3 Comparison of T2 spectrum inversion results with different αSNR

从图3中可以看出，自适应谱随着信噪比的变化分别与构造谱、δ1、δ2、δ3谱重合，并且自适应谱总能最接近构造谱。以某一固定截断奇异值得到的T2谱曲线在不同信噪比条件下曲线差异巨大，并且不能保证准确性，这说明传统固定截断奇异值方法在噪声干扰的影响下稳定性较差。自适应截断奇异值方法能够根据噪声干扰的影响自动选取截断值，去掉小的非零奇异值以增强稳定性，不会因噪声干扰程度不同对结果产生较大影响，抗噪能力强，并且峰值大小与峰值所对应的弛豫时间较为准确。

2.2 非负约束方法

对比在信噪比αSNR分别为10、100时，非负最小二乘约束、简单迭代法非负约束(迭代次数n=1000)和正则化因子非负约束下的反演效果，如图4所示。

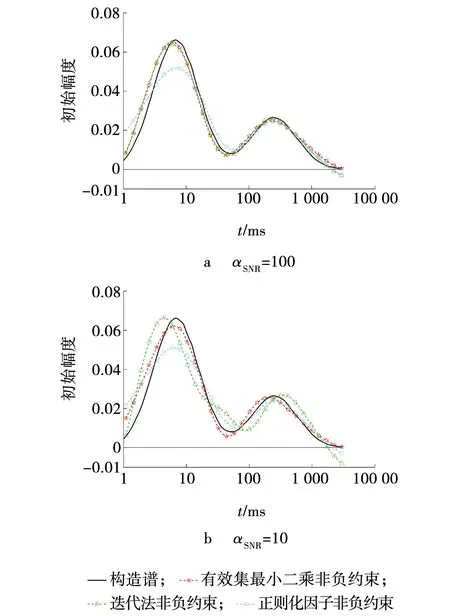
图4 不同信噪比下非负约束对比 Fig. 4 Non-negative constraint comparison of different αSNR

与构造谱对比，在迭代次数较少时，简单的迭代法非负约束和正则化因子非负约束在T2谱尾端均出现幅度值小于零值的情况，并且随信噪比的降低，迭代法非负约束出现负值幅度变大的情况。有效集非负最小二乘法非负约束T2谱尾端未出现负幅度值，且曲线平滑，与构造谱曲线重合度较高。

在迭代次数较少时，简单迭代方法无法完全实现非负约束，正则化因子法为了实现非负约束，牺牲了解的准确性。非负最小二乘法在进一步保证解的准确性的同时实现了完全的非负约束。

简单迭代法和正则化法要实现完全非负约束需要牺牲大量的计算时间。而由有效集非负最小二乘法步骤可知，该方法无需迭代，有计算速度快的优点。

3 实 例

某井在2 170～2 230 m井段核磁共振测井，利用新旧两种T2谱反演方法得出的结果对比如图5所示。

图5 不同方法下T2谱反演结果对比Fig. 5 Comparison of T2 spectrum inversion results of different methods

图5中第一道为深度道；第二道为自然伽马曲线；第三道SPECTA为利用自适应截断奇异值结合有效集非负约束法反演得到的T2谱；第四道DISTA为CIFLog测井处理解释平台反演得到的T2谱。

由图5可以看出，SPECTA和DISTA反演结果整体基本一致。在深度2 170～2 182 m井段，SPECTA在弛豫时间30～3 000 ms处相比DISTA能够清晰地反映出完整的峰值形态。在深度2 200～2 210 m井段，SPECTA和DISTA两者形态基本相同，但SPECTA较为平缓，未出现较大幅度波动。深度2 217～2 226 m井段为泥岩段，自然伽马曲线幅度较高，SPECTA和DISTA两者在低弛豫时间处均出现明显幅度。

利用自适应截断奇异值结合有效集非负约束法反演出的T2谱具有精细的结构，曲线平滑且连续。该方法在处理速度上也有较好的表现，能够在几秒钟内完成对整口井的T2谱反演处理工作。

4 结 论

(1)自适应截断奇异值方法能够在保证T2谱稳定的前提下，最大限度提取回波串中的有用信息。在噪声水平变化时，能够根据噪声自动调节奇异值个数，使反演T2谱能够在平均值意义下达到较高的精度。

(2)有效集非负约束方法能以有限的运算次数，快速实现解的非负约束，得到连续的非负解，该方法相比迭代非负约束方法和正则化因子非负约束方法准确性高，且迭代次数少，运算速度快。

(3)自适应截断奇异值结合有效集非负约束方法能够均衡反演结果的准确性与稳定性，较为精准地反映各弛豫时间信号大小。该方法具有准确度高、稳定性好、抗噪能力较强和反演速度快的特点，能够满足野外核磁共振测井资料处理的要求。