制冷机组蒸发器系统的Elman神经网络预测模型
2020-07-13沈显庆黄习恒
沈显庆, 黄习恒
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
随着经济快速发展,制冷设施在生产生活变得越来越重要。尤其在医疗药物、特殊材料、高端食材等方面对温度精度要求更高。超过预警温度,将会造成极大损失。蒸发器作为制冷机组冷库温度精度控制最直接的部分,冷库温度超过预警温度,即视为蒸发器系统故障,在故障发生之前根据出现的微小征兆准确预测故障,将会有重大的意义[1]。韩华等[2]提出一种复合故障诊断模型,利用遗传算法与带参数优化的支持矢量机结合,提高故障诊断正确率,但未对故障预测问题进一步分析。蔡博伟等[3]提出了一种基于前馈神经网络的空调系统焓差试验台故障预测模型,取得了较好的成果,但未对制冷系统具体部位故障预测进行分析,且故障预测特征值精度未提及。基于以上研究现状,笔者以某一针对特殊食材设计的高精度低温冷库为研究对象,其食材保存温度为-29 ℃,可允许温差为0.5 ℃,超过预警温度1 h即会导致食物变质。通过Matlab系统仿真研究,使用一步预测模式,建立基于Adam算法改进的Elman神经网络设计预测模型,对比分析网络的预测性能。
1 一步预测输入输出模式
1.1 样本参数的选取
制冷机组主要组成部分为压缩机、冷凝器、蒸发器、节流阀等。制冷工作环境下,蒸发器及其部件位于室内,经制冷剂作用调节室内温度,冷库温度与蒸发器系统有着直接关系。通过对蒸发器系统数据样本集分析,按照输入数据是否与系统输出指标有明确因果关系,选取蒸发器指标参数如下5个:风机排水管温度、蒸发器冷却液进口温度、风机托水盘温度、低温霜温和压缩机进口温度。由于冷库温度每5 min测量一次,故30 min内有6组数据,6组数据中冷库温度均处于[-29.5,-28.5] ℃范围中,即视系统在30 min内处于正常工作状态;否则即视系统在30 min内出现故障。
1.2 输入输出设置
在传统故障预测中,输入为当前时刻的实际值,输出为下一时刻的估计值[4]。而制冷机组各特征值数据均呈连续性变换,因此后一时刻的值一定和前一时刻值有关。利用传统的输入输出模式设置不能反映出此现象,且会使预测结果不够理想。
一步预测模式是指利用前一时刻输出的实际值和当前时刻的特征量实际值来作为输入,以下一时刻的估计值作为输出。此预测模式可使训练模型训练次数减少,预测准确率更高。
由于蒸发器各温度参数和冷库温度均是呈连续性变化,因此后一时刻的值一定和前一时刻值有关。现使用一步预测模式将预测时刻前30 min内6次冷库温度实际值和预测时刻的5个蒸发器指标参数作为网络的输入样本数据,预测时刻开始30 min内6次冷库温度预测值作为输出。
原始数据归一化[5]处理后的值如表1所示,其中,风机排水管温度为t1,蒸发器冷却液进口温度为t2,风机托水盘温度为t3,霜温为t4,压缩机进口温度为t5,30 min内冷库温度预测次数为n。

表1 归一化后数据
2 Adam算法
Adam是一种自适应动量的随机优化方法。Adam算法与传统随机梯度下降不同。其不同于传统随机梯度下降以单一的学习率更新所有权重,而是通过计算梯度的一阶矩估计和二阶矩估计[6],为不同的参数设置相应的自适应学习率,从而减少误差,提高优化效率。
Adam算法公式为[7]
mt=β1mt-1+(1-β1)gt,
式中:gt——随机目标函数的梯度;
mt——梯度的一阶矩估计量;
vt——梯度的二阶矩估计量。
Adam算法中常给定超参数β1=0.9、β2=0.999。
对变量mt和vt进行偏差修正:
Adam的参数更新公式为
Adam算法中常给定参数ε=10-8、α=0.01。
3 Elman神经网络预测方法
Elman神经网络是一种典型的递归神经网络,它采用局部反馈连接,所表示的是一个动态过程,具有一定的“记忆”能力,非常适合处理时间序列的预测问题。其一般具有四层结构,输入层、隐含层、状态层、输出层[8-9]。状态层是一种特殊的隐含层,该层从隐含层接收反馈信号,再通过状态层神经元输出前向传递至隐含层,完成局部反馈连接,并使网络具有一定的记忆能力,使网络收敛速度加快。
Elman神经网络结构如图1所示。包括四层结构,输入层、隐含层、状态层、输出层。其结构在BP神经网络基础上加入了反馈连接单元,采用反向传播方式。文中使用Adam算法,通过自适应调节学习率,对各层神经元之间权值不断修正使误差减小,从而得到精确期望输出值。

图1 Elman神经网络结构Fig. 1 Elman neural network structure
文中设置输入层神经元数为11个,j为(1,2,…,11);输出层神经元个数为6,k为(1,2,…,6)。隐含层神经元数对网络性能影响很大,综合考虑网络性能和训练速度,经实验设定隐含层神经元数为25个,i=(1,2,…,25),状态层神经元数为25个,m=(1,2,…,25)。
图1中:xj为输入序列数据,其中x1~x5分别表示预测时刻蒸发器5个指标参数:风机排水管温度、蒸发器冷却液进口温度、风机托水盘温度、低温霜温和压缩机进口温度,x6~x11分别表示预测时刻前30 min内6次冷库温度实际值;yk为输出层输出数据,y1~y6分别表示预测时刻后30 min内6次冷库温度预测值。
Elman神经网络数学模型为
隐含层输入:
式中:ωim——状态层到隐含层之间的权值;
yom——状态层的输出;
ωij——输入层到隐含层之间的权值;
xj——输入序列数据。
隐含层神经元S型正切激活函数
输出层神经元S型对数激活函数
隐含层、状态层、输出层输出:
yom=yoi+αyom,
式中:α——状态层自反馈增益;
ωki——连接隐含层到输出层之间的权值。
4 仿真结果与分析
分别使用传统BP神经网络和改进后Elman神经网络两种方法对制冷机组故障预测系统模型进行训练、测试,得到两个预测模型,通过对比所得输出数据指标,判断网络预测的精确度。
文中两种方法所用样本数据完全相同。制冷机组预设冷库温度为-29 ℃,允许偏差为0.5 ℃,当冷库温度在区间[-29.5,-28.5] ℃,即视蒸发器系统为正常工作状态,除此之外皆视为故障运行状态。
样本采集时间为24小时,每30 min一组共47组数据,其中第1~24组的冷库温度实际值和第2~25组的蒸发器指标参数,共24组样本对作为训练样本;后23组样本对作为预测样本。
4.1 训练对比
经实际训练与测试结果对比,传统BP神经网络设置训练次数为1 000、误差为0.001 5、隐含层神经元个数为23时,网络预测效果最好。改进后Elman神经网络设置训练次数为3 000、误差为0.001、隐含层神经元个数为25时,网络预测效果最好[10]。分别使用传统BP神经网络和改进Elman神经网络对预测输出与实际输出对比。
4.1.1 训练组
传统BP网络训练组输出与实际输出的对比,以及改进Elman网络训练组输出与实际输出对比如图2所示。

图2 不同网络训练组Fig. 2 Different network training group
4.1.2 测试组
传统BP神经网络测试组输出与实际输出的对比,以及改进Elman网络测试组输出与实际输出对比如图3所示。
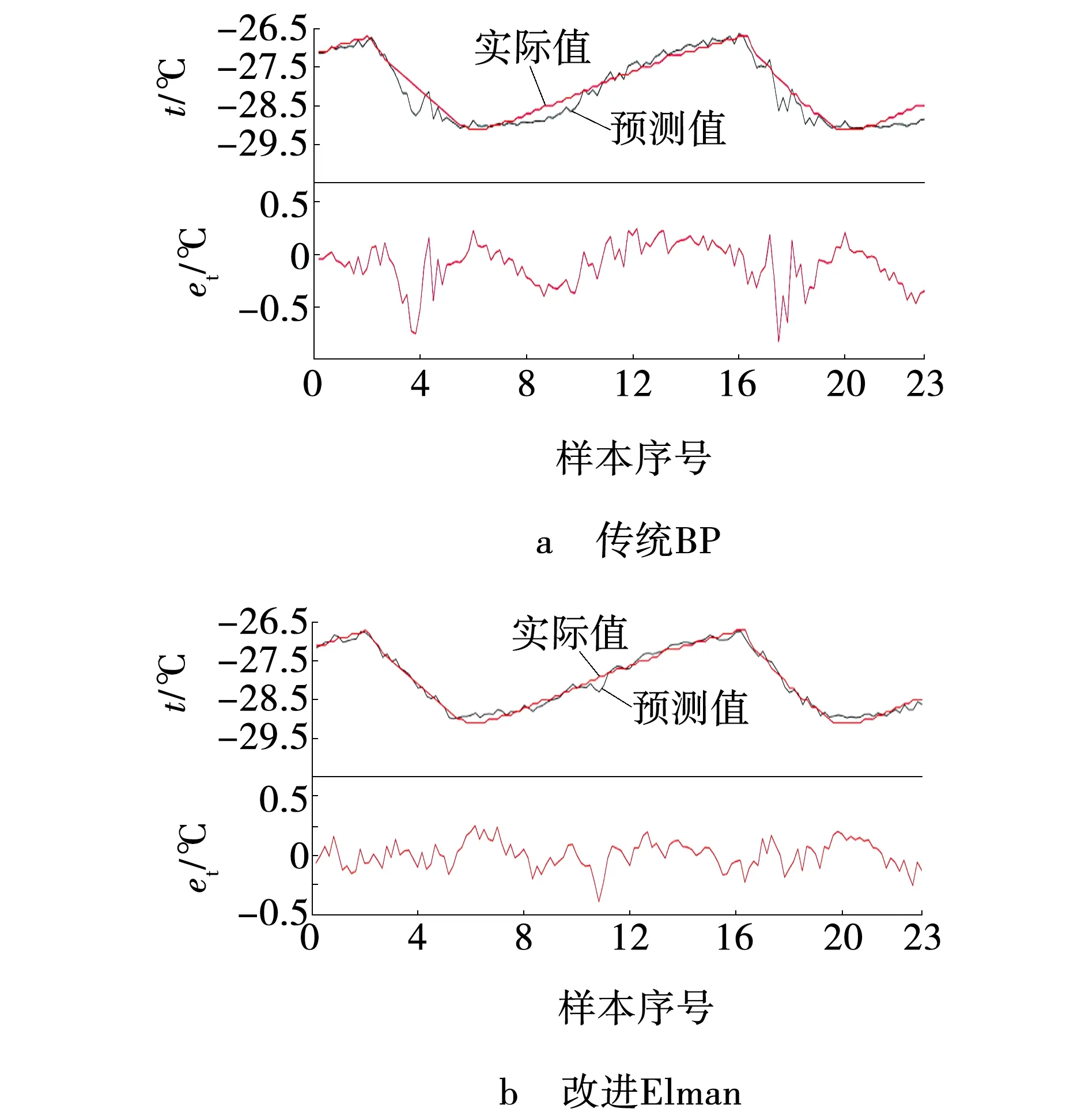
图3 不同网络测试组Fig. 3 Different network test group
通过对比以上4组数据的输出结果,在所用样本完全相同的情况下,改进Elman神经网络模型预测效果更好。
4.2 网络预测的精确度
为提高网络预测精度,正常状态下预测输出值与实际值误差小于0.25 ℃,且预测输出值在区间[-29.5,-28.5]℃中,视为预测正确,否则视为预测错误;故障状态下预测输出值与实际值误差小于0.25 ℃,且预测输出值不在区间[-29.5,-28.5]℃中,视为预测正确,否则视为预测错误。网络性能指标公式[11]:
预测正确率
式中:Tn——正常状态下预测正确次数;
Fn——正常状态下预测错误次数;
Tf——故障状态下预测正确次数;
Ff——故障状态下预测错误次数。
预测误报率
故障预测能力
此指标为正确预测在故障状态与实际的故障状态之比,既故障预测的正确率,体现了系统预测故障的能力。
预测故障可信度
此指标为正确预测到故障状态与所有预测到故障状态之比,比如预测到一组数据显示为故障状态,则其实际故障的概率为P,它体现了预测为故障时的可信程度。
文中传统BP网络和改进Elman网络预测模型精度数据:Tn分别为5、7;Fn分别为3、1;Tf分别为9、14;Ff分别是6、1。
对比两种网络预测模型,以上性能指标如表2所示。

表2 网络性能指标对比
从表2可以得出,预测正确率上,改进Elman神经网络比传统BP神经网络准确率提高了30.43%;预测误报率上,降低了30.43%;故障预测能力上,提高了33.33%;预测故障可信度上,提高了18.33%。综上可以看出,经一步预测模式设置,基于Adam算法优化的Elman神经网络各项预测精度均比传统BP神经网络有所提高。
5 结束语
文中分别应用一步预测模式构建了Adam算法改进的Elman神经网络故障预测模型和传统BP神经网络预测模型,对制冷机组蒸发器系统故障预测进行了对比分析。由误差结果及各项性能指标得出,优化改进后的Elman神经网络预测模型对制冷机组蒸发器系统故障预测效果更好。
