巧借曲线切线放缩证明函数不等式

湖南省长沙市第一中学

一、指数函数的切线放缩

指数函数y=ex在x=0处的切线方程为y=x+1，从图1可以看出，函数y=x+1的图象(除x=0)恒在y=ex的下方，因此ex≥x+1，证明如下：

令f(x)=ex-x-1，则f′(x)=ex-1.当x＞0时，f′(x)＞0，f(x)单调递增；当x＜0时，f′(x)＜0，f(x)单调递减，所以f(x)≥f(0)=0，所以ex≥x+1，当且仅当x=0时等号成立.

图1

例1已知函数

(1)求函数f(x)的单调区间；(2)当x＞0，证明不等式：(ex-1)ln(x+1)＞x2.

解(1)函数f(x)的定义域为(-1,0)∪(0,+∞).所以令则当x ∈(-1,0)时，g′(x)＞0，函数g(x)单调递增；当x ∈(0,+∞)时，g′(x)＜0，函数g(x)单调递减，所以当x ∈(-1,0)∪(0,+∞)时，g(x)＜g(0)= 0，即f′(x)＜0，所以函数f(x)单调递减区间为(-1,0)，(0,+∞).

(2)当x＞0时，要证明(ex-1)ln(x+1)＞x2，只需证明只要证明f(x)＞f(ex-1)，因为当x＞0时，ex＞x+1，即x＜ex-1，由(1)知在(0,+∞)单调递减，所以f(x)＞f(ex-1)，所以不等式(ex-1)ln(x+1)＞x2成立.

评注若本题第(2)问通过构造函数h(x)=(ex-1)ln(x+1)-x2，对h(x)进行求导，由于h′(x)的结构复杂，难以判断它的零点和相应区间符号，因此对要证明的不等式进行代数变形，构造出不等式两边具有相同结构的代数式，转化为证明f(x)＞f(ex-1)，最后利用第(1)问中函数f(x)的单调性以及指数函数y=ex的切线放缩(ex≥x+1)来证明不等式.

例2(2014年高考全国I卷理科第21题)设函数曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.

(1)求a,b；

(2)证明：f(x)＞1.

解(1)a=1,b=2.(过程略)

评注本题有多种证明方法，这里选择先将要证明不等式进行代数变形，利用指数函数y=ex在x=1处的切线y=ex放缩(ex≥ex)来证明不等式右边非正，然后证明不等式左边函数非负，由于等号不能同时取到，故不等式得证.一般地，指数函数y=ex常常可以利用其在x=x0处的切线y=ex0x+(1-x0)ex0放缩得到不等式

二、对数函数的切线放缩

对数函数y=lnx在x=1处的切线方程为y=x-1，从图2可以看出，函数y=x-1的图象(除x=1)恒在y=lnx的上方，因此lnx≤x-1，证明如下：

图2

令f(x)= lnx-x+1，则当x＞1时，f′(x)＜0，f(x)单调递减；当0＜x＜1时，f′(x)＞0，f(x)单调递增，所以f(x)≤f(1)= 0，所以lnx≤x-1，当且仅当x=1时等号成立.

例3已知函数f(x)=2x-lnx.

(1)求函数f(x)的单调区间；(2)证明：f(x)＜

解(1)函数f(x)的定义域为当时，f′(x)＜0，f(x)单调递减；当时，f′(x)＞0，f(x)单调递增，所以f(x)的单调递减区间为递增区间为

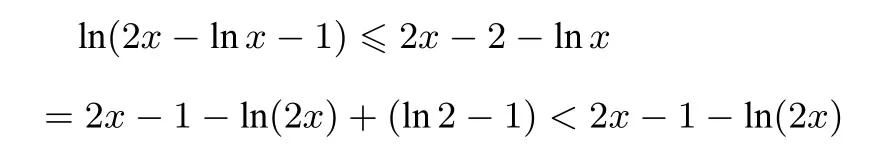
评注本题若选择移项构造新函数求导，再求新函数的极值和单调区间将十分困难，因此另辟蹊径，先移项再取对数，利用对数函数的切线不等式来放缩证明.一般地，对数函数y=lnx常常可以利用其在x=x0处的切线放缩得到不等式

三、幂函数的切线放缩

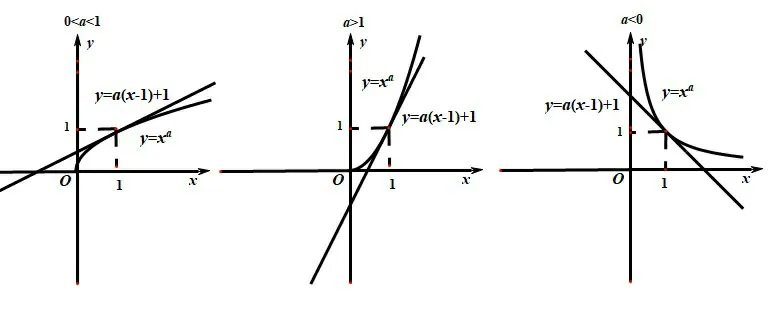
幂函数y=xa(x＞0)在x=1处的切线方程为y=a(x-1)+1，由图3可以看出，当0＜a＜1时，函数y=a(x-1)+1的图象(除x=1)在y=xa的上方，因此，当0＜a＜1时，xa≤a(x-1)+1(x＞0)；当a＞1或a＜0时，函数y=a(x-1)+1的图象(除x=1)在y=xa的下方，因此，当a＞1或a＜0时，xa≥a(x-1)+1(x＞0).

证明如下：令f(x)=xa-a(x-1)-1，则f′(x)=

当0＜a＜1，x ∈(0,1)时，f′(x)＞0，f(x)单调递增；x ∈(1,+∞)时，f′(x)＜0，f(x)单调递 减，所以f(x)≤f(1)= 0，即xa≤a(x-1)+1；当a＞1或a＜0，x ∈(0,1)时，f′(x)＜0，f(x)单调递减；x ∈(1,+∞)时，f′(x)＞0，f(x)单调递增，所以f(x)≥f(1)= 0，即xa≥a(x-1)+1.

例4已知函数f(x)=(1+x)α，其中α为常数，且0＜α＜1，设函数f(x)在点P(0,1)处的切线方程为y=g(x).

(1)证明：对于任意的正实数x，都有f(x)＜g(x)；

(2)若0＜a＜1,0＜b＜1，证明：ab+ba＞1.

证明(1)因为f′(x)=α(1+x)α-1，故f′(0)=α，函数f(x)在点P(0,1)处的切线方程为y-1 =αx，即g(x)=αx+1.

令h(x)=f(x)-g(x)=(1+x)α-αx-1，则h′(x)=α(1+x)α-1-α=α[(1+x)α-1-1]，因为x＞0，0＜α＜1，所以(1+x)α-1＜(1+x)0=1，所以h′(x)＜0，所以h(x)在(0,+∞)上单调递减；所以h(x)＜h(0)=0，所以f(x)＜g(x).

(2)由第(1)问可知，当0＜α＜1，x ∈(0,+∞)时，(1+x)α＜αx+1.因为0＜a＜1，0＜b＜1，所以所以

评注本题第(1)问由函数f(x)在x=0处的切线放缩可以得到：当0＜α＜1，x ∈(0,+∞)时，(1+x)α＜αx+1.第(2)问要证明ab+ba＞1，根据要证明的不等式方向，将不等式左边的两项分别取倒数后再巧妙利用第(1)问中的切线放缩即可快速证明.

四、三角函数的切线放缩

正弦函数y=sinx在x=0处的切线方程为y=x，正切函数y=tanx在x=0处的切线方程为y=x，从图4可以看出，当时，y=x在正弦函数y=sinx的上方，在y=tanx的下方，因此当时，sinx＜x＜tanx，证明如下：

图4

令f(x)=sinx-x，则f′(x)=cosx-1＜0，从而f(x)在上单调递减，所以f(x)＜f(0)= 0，即sinx＜x.令g(x)= tanx-x，x ∈则g′(x)=从而g(x)在上单调递增，所以g(x)＞g(0)= 0，即x＜tanx.所以当时，sinx＜x＜tanx.

例5已知0＜x＜π，求证：

证明由题可知

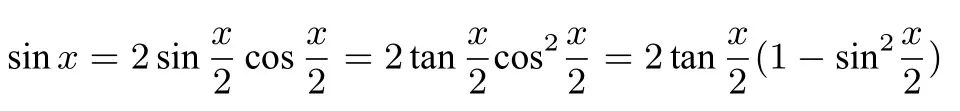
所以

评注本题选择将正弦函数用二倍角公式展开，再借助正弦函数和正切函数在x=0处的切线不等式sinx＜x＜tanx进行放缩证明，十分简洁.当然，直接做差构造新函数f(x)=通过多次求导可以证明f(x)大于0.

五、其它初等函数的切线放缩

例6(2015年高考天津卷理科第20题)已知函数f(x)=nx-xn,x ∈R，其中n ∈N∗,n≥2.

(1)讨论f(x)的单调性；

(2)设曲线y=f(x)与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g(x)，求证：对于任意的正实数x，都有f(x)≤g(x)；

(3)若关于x的方程f(x)=a(a为实数)有两个正实根x1,x2，求证：

解(1)略.

证明(2)设点P的坐标为(x0,0)，则

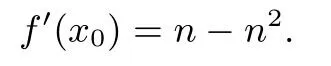
曲线y=f(x)在点P处的切线方程为y=f′(x0)(x-x0)，即g(x)=f′(x0)(x-x0).令F(x)=f(x)-g(x)，即

则F′(x)=f′(x)-f′(x0).由(1)知f′(x)=-nxn-1+n在(0,+∞)上单调递减，故F′(x)在(0,+∞)上单调递减.又因为F′(x0)= 0，所以当x ∈(0,x0)时，F′(x)＞0，当x ∈(x0,+∞)时，F′(x)＜0，所以F(x)在(0,x0)内单调递增，在(x0,+∞)上单调递减，所以对于任意的正实数x，都有F(x)≤F(x0)= 0，即对于任意的正实数x，都有

实验材料是采购于武汉大学典藏中心的人前列腺癌PC3 细胞株。雷公藤内脂醇采购于美国Sigma公司，用无菌双蒸水配制为1.0 mg/ml的储备液，保存在-20°的冰柜内备用。新生牛血清、DMEM培养液、胰蛋白酶购于美国BRL Gibco公司。

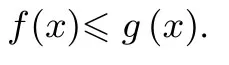
(3)不妨设x1≤x2.由(2)知g(x)=(n-n2)(x-x0).设方程g(x)=a的根为x′2，可得由(2)知g(x2)≥f(x2)=a=g(x′2)，可得x2≤x′2.

类似地，设曲线y=f(x)在原点处的切线方程为y=h(x)，可得h(x)=nx，当x ∈(0,+∞)，f(x)-h(x)=-xn＜0，即对于任意的x ∈(0,+∞)，f(x)＜h(x).设方程h(x)=a的根为x′1，可得因为h(x)=nx在(-∞,+∞)上单调递增，且因此

由此可得

因为n≥2，所以

评注由于第(3)问如果求解f(x)=a的实根x1,x2将十分困难.因此在第(2)问的基础上，巧妙借助函数f(x)与x轴两个交点处的切线，将难以求解的曲线与直线的交点坐标转化为易于求解的切线与直线的交点坐标，从而证明不等式.

例7已知函数

(1)求函数f(x)在x=0处的切线方程；

(2)证明：当x≥0时，g(x)-3f(x)≥1.

解(1)因为

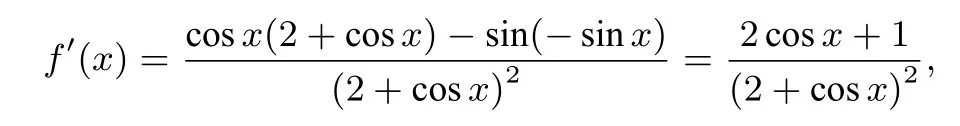
(2)令h(x)=则

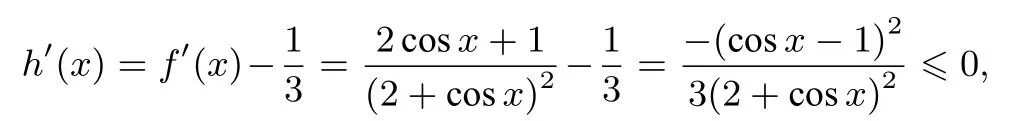
所以h(x)在[0,+∞)单调递减，所以h(x)≤h(0)= 0，即又因为g(x)=ex≥x+1，所以g(x)-3f(x)≥证毕.

评注本题第(2)问如果对不等式左边函数通过多次求导或者设而不求等方法，都无法求得最小值，因此，巧妙借助第(1)问函数f(x)的切线，证明函数f(x)在切线的下方(除切点)，利用切线放缩，可以快速简洁的证明不等式.

函数不等式的证明难度大、技巧性强.切线放缩为解决这类问题提供了一种可供选择的方法，借助曲线切线放缩，可以将复杂的函数曲线转化为简单的一次函数，从而达到化曲为直、化繁为简的目的.学生在解题过程中一定要认真分析、勇于尝试，多积累一些常用的解题方法和技巧，注重思维深度和广度的培养，不断提升自身解题能力和数学核心素养.