最值中的定值问题*

北京市第十二中学高中部

1.试题

题目(2020年1月南京市、盐城市高三第一次模考)设椭圆的左、右焦点分别为F1，F2，离心率是e，动点P(x0,y0)在椭圆C上运动，当PF2⊥x轴时，x0=1，y0=e.

(1)求椭圆C的方程；

(2)延长PF1，PF2分别交椭圆C于点A，B(A,B不重合)，设求λ+µ的最小值.

试题考查了椭圆的标准方程、几何性质、直线和椭圆的位置关系、向量的坐标运算以及最值问题，考查了数学运算、直观想象等数学素养，考查了坐标法的应用以及分析问题与解决问题的能力.试题解法多样，内涵丰富，符合新课标理念.第(1)问求得椭圆C的方程为下面重点谈一下第(2)问的解法以及所蕴含的定值问题.

2.解法探究

解法1设A(x1,y1)，B(x2,y2)，由(1)问得F1(-1,0)，F2(1,0).设直线PA的方程为x=ty-1，与联立，得(t2+2)y2-2ty-1=0，所以因为所以(-1-x1,-y1)=λ(x0+1,y0)，即y1=-λy0，于是因为点P既在直线PA上，又在椭圆C上，所以x0=即ty0=x0+1，x02+2y02=2，于是同理，由得所以因为0≤x02＜2，所以当x0=0时，有最小值为故λ+µ的最小值为

解法2设A(x1,y1)，B(x2,y2)，由(1)问得F1(-1,0)，F2(1,0).因为所以(-1-x1,-y1)=λ(x0+1,y0)，于是x1=-(λx0+λ+1)，y1=-λy0.因为点A在椭圆C上，所以所以1，即

因为点P在椭圆C上，所以代入，得整理得2λ(λ+1)x0=-(3λ-1)(λ+1).由已知得λ-1，所以2λx0=1-3λ，解得同理，由得以下同解法1.

点评解法1，2都是把向量关系转化为坐标关系，然后借助点P的坐标表示出λ+µ，最后根据平方数非负求得最值.不同的是解法1 联立直线PA、PB与椭圆的方程，借助韦达定理化简；解法2 根据点A、P在椭圆上，把它们的坐标代入椭圆方程处理，两种方法殊途同归，体现了设而不求的思想.

解法3以F1为极点，射线F1O为极轴建立极坐标系，由(1)问可得焦点到相应准线的距离p=1，所以椭圆C的极坐标方程为

设P(ρ1,θ)(0＜θ＜π)，A(ρ2,θ+π)，则

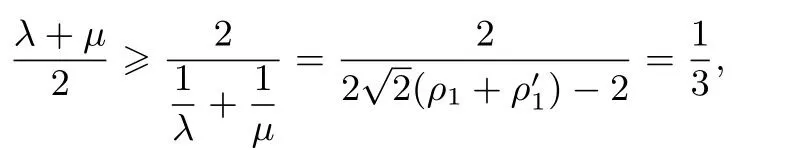
点评由于PA、PB为焦点弦，所以解法3 借助椭圆的极坐标方程及定义处理，最后运用均值不等式求得最值，体现了创新性.

3.题目中的定值及推广

性质1已知椭圆的左、右焦点分别为F1，F2，动点P在椭圆C上运动，延长PF1，PF2分别交椭圆C于点A，B(A，B不重合)，设则λ+µ为定值6.

如果将椭圆一般化，其他条件不变，那么λ+µ为何值呢?经过探究，有：

性质2已知椭圆的左、右焦点分别为F1，F2，动点P在椭圆C上运动，延长PF1，PF2分别交椭圆C于点A，B(A，B不重合)，设则λ+µ为定值

证明设P(x0,y0)，A(x1,y1)，B(x2,y2)，F1(-c,0)，F2(c,0)(c＞0).设直线PA的方程为x=ty-c，与联立，得(b2t2+a2)y2-2ctb2y-b4=0，所以因为所以(-c-x0,-y0)=λ(x1+c,y1)，即y0=-λy1，于是

因为点P既在直线PA上，又在椭圆C上，所以x0=ty0-c，即于是

如果把两个焦点变为关于原点对称的两个定点，也有相应的定值性质.

性质3已知动点P在椭圆上运动，定点M(-m,0)，N(m,0)(m＞0且ma)，直线PM，PN分别交椭圆C于另一点A，B(A，B不重合)，设则λ+µ为定值

证明设P(x0,y0)，A(x1,y1)，B(x2,y2)，直线PA的方程为x=ty-m，与联立，得(b2t2+a2)y2-2tmb2y+b2m2-a2b2=0,所以因为所以(-m-x0,-y0)=λ(x1+m,y1)，即y0=-λy1，于是

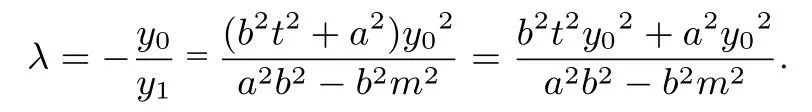
因为点P既在直线PA上，又在椭圆C上，所以x0=ty0-即于是

注当m=c时，

这是性质2的结论，所以性质2是性质3的特殊情况.

由椭圆类比圆、双曲线、抛物线，有下面的结论.

性质4已知动点P在圆O:x2+y2=R2(R＞0)上运动，定点M(-m,0)，N(m,0)(m＞0且mR)，直线PM，PN分别交圆O于另一点A，B(A,B不重合)，设则λ+µ为定值

性质5已知动点P在双曲线0,b＞0)上运动，定点M(-m,0)，N(m,0)(m＞0且ma)，直线PM，PN分别交双曲线C于另一点A，B(A，B不重合)，设则λ+µ为定值

性质6已知动点P在抛物线C:y2=2px(p＞0)上运动，定点M，N关于原点O对称，直线PM，PN分别交抛物线C于另一点A，B，设则λ+µ为定值0.

证明设P(x0,y0)，A(x1,y1)，B(x2,y2)，M(-m,0)，则N(m,0).设直线PA的方程为x=ty-m，与y2=2px联立，得y2-2pty+2pm=0，所以y1y0=2pm.因为所以(-m-x0,-y0)=λ(x1+m,y1)，即y0=-λy1，于是.同理，由得所以λ+µ=0，故结论得证.