基于集成回声状态网络Fisher核的时间序列分类算法

王 劲 松

(中国科学技术大学计算机科学与技术学院中国科大-伯明翰大学智能计算与应用联合研究所 安徽 合肥 230027)

0 引 言

在许多实际应用领域都会产生大量的时序数据，比如股票交易[1]、电力系统[2]和工业观测[3]等。时序数据是一种结构化的数据，具有高维、变长、数值之间存在时序依赖关系等特点。研究人员提出了很多有效的时间序列分类算法。早期基于欧氏距离和动态时间规整距离的最近邻算法采用欧氏距离或动态时间规整距离来度量两个时序样本之间的距离[4-6]，虽然欧氏距离计算在某些情况下比较高效，以及动态时间规整距离算法可以解决时序变长问题，但当前基于距离的方法本质上还是基于点与点的比较，难以捕捉到隐藏在序列中动态的时序依赖信息。基于特征的方法的核心思想是采用各种技术从原始时序数据中提取出具有鉴别力的特征[7-8]。尽管相关实验表明基于特征的方法可以很好地提取序列中的局部信息，但是巨大的特征搜索空间和繁重的数据预处理使得此类方法时间开销大。

另一类基于模型的方法先是用一个特定的生成模型对时序数据的分布进行拟合，为每条时序样本学习一个函数模型，然后基于函数模型之间的差异来度量原始时序样本之间的距离，例如：基于隐马尔可夫模型的概率积核[9]、Fisher核[10]以及基于高斯混合模型的散度核[11]等。相关研究工作[12]讨论并分析了此类方法度量结构化时序数据的优势。由于数据背后指定的生成模型的假设有时过于严格，限制了模型对时序样本的近似能力。近几年，一类高效的非线性储蓄池模型被用来处理时间序列，其中回声状态网络(Echo State Network，ESN)模型[13]受到较多关注。动态状态规整算法[14]将原始的时序数据映射到储蓄池的隐状态空间中，然后基于经典的动态时间规整距离来度量转换的隐状态序列，提高了模型的分类性能。文献[15]利用ESN的读出权重对噪音数据进行分类，验证了回声状态网络具有一定的鲁棒性。Ma等[16]用时变输出函数替换ESN的输出权重，并将时间聚合运算引入输出层，将时间信号投影到离散类标签中。

尽管基于回声状态网络模型的时序分类算法利用非线性的储蓄池来拟合时序动态的生成机制，然而对于这种非欧的模型空间，传统的欧氏距离度量方法已经不能满足要求。文献[17-18]表明学习出有鉴别力的距离度量方式有助于提高模型的分类能力。此外，文献[19]证明了在单个数据表示的情况下，采用集成方法可以提高时序算法的分类性能。目前基于ESN的时间序列算法分类准确度还有待提高，究其原因，基于单个回声状态网络模型的时间序列分类算法不能很好地拟合数据复杂的分布结构，因此，本文尝试引入AdaBoost集成方法[20]训练出多个模型来缓解这一问题。

本文提出一种基于集成回声状态网络和Fisher核的时间序列分类算法(Fisher Kernel based on Integration of ESNs，FKIESN)。该模型先用回声状态网络模型对时间序列进行建模，捕捉序列中隐藏的动态信息，然后在模型的参数空间中采用Fisher核来度量函数模型之间的差异。由于回声状态网络是一个预测模型而非分类模型，传统的AdaBoost分类算法不能直接应用，本文引入了AdaBoost回归框架训练出多个模型，在特征层面上完成加权集成，提高了模型的分类能力。

1 回声状态网络与Fisher核

1.1 回声状态网络

如图1所示,回声状态网络是循环神经网络的一种改进版本，主要由输入层、水库层和输出层组成。三层的神经元数量分别为D、N和O。图中，实线箭头表示固定和随机连接，虚线箭头表示可训练的连接。

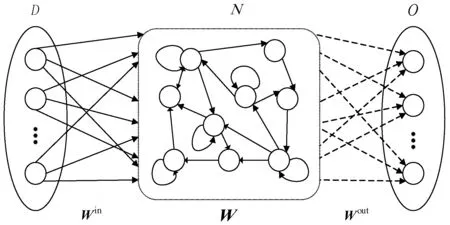
图1 标准回声状态网络结构图

不考虑输出层到水库层连接的简化回声状态网络可以通过下式进行训练：

x(t+1)=f(Wx(t)+Winu(t))

y(t+1)=Woutz(x(t+1))

(1)

式中：Win∈RN×D代表输入神经元到水库神经元的连接权值;W∈RN×N表示水库内部神经元之间的连接权值；Wout∈RO×(N+D)代表水库神经元到输出神经元的连接权值(读出映射)；u(t)∈RD是网络当前时刻的输入；x(t)∈RN表示当前时刻水库的状态；z(t)=[x(t);u(t)]表示考虑输入时的当前系统状态；f(·)表示水库神经元的激活函数，一般是tanh函数。防止初始瞬态的影响，从tmin+1时刻开始保存系统状态Z=[z(tmin+1),z(tmin+2),…,z(tmin+l)]，其中l代表训练样本的长度。假设期望输出矩阵为Y=[y(tmin+1),y(tmin+2),…,y(tmin+l)]，则通过最小二乘法可学习到读出映射：

Wout=(ZTZ)-1ZTY

(2)

为了防止过拟合，通常引入正则化参数，则读出映射为：

Wout=(ZTZ+λI)-1ZTY

(3)

式中：λ是正则化系数，I是单位矩阵。

回声状态网络两个典型的特点是拥有一个不需要训练的高维非线性动态水库和一个可以高效训练的读出映射，其中输入权值矩阵和水库权值矩阵都是随机化产生，而读出映射通过线性回归训练得到。通过考虑当前输入和先前的历史信息，回声状态网络模型可以捕捉到隐藏在时序数据中的动态信息。回声状态网络是一个预测模型而非分类器，尽管研究学者已经提出了一些基于回声状态网络的高效分类模型，该领域还有很多值得研究的问题。

1.2 Fisher核

生成方法拟合类条件概率密度函数，而判别方法专注于直接分类。Fisher核[21]能够结合生成方式和判别方式的优势，假定P(u|θ)为一个概率生成模型，其中θ是模型参数，则Fisher核可将时序样本u编码成一个费希尔分数向量：

Uu=▽θlog(P(u|θ))

(4)

给定两条时间序列样本a和b，其对应的费希尔分数分别为Ua和Ub，则Fisher核测量的距离为：

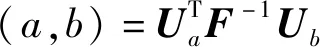
(5)

式中：F=Es{▽θlog(P(S|θ))▽θlog(P(S|θ))T}为费希尔信息矩阵；S为训练样本集；Es是期望。似然函数通常比较复杂，很难计算对应的期望，通常采用训练集进行经验期望估计，则：

(6)

2 算法设计

2.1 基于回声状态网络的Fisher核

根据以上关于回声状态网络和Fisher核的介绍，本文利用回声状态网络来建模时间序列样本，在回声状态网络模型的参数空间中利用Fisher核来度量函数模型之间的差异，并给出相应的公式推导。

引入噪音假设的基于回声状态网络的概率生成模型如下：

x(t+1)=f(Wx(t)+Winu(t))

y(t+1)=Woutz(x(t+1))+b+ε(t)

(7)

式中：b为截距。

假设独立同分布，噪音模型ε(t)服从高斯分布:

ε(t)=N(0,σ2I)

(8)

则u(t+1)的条件概率为：

P(u(t+1)|u(1),u(2),…,u(t))=P(u(t+1)|x(t))=

(9)

给定一条长度为l的时间序列，用p(u(1,2,…,l))来简化表示模型的似然函数p(u(1),u(2),…,u(l))，则似然函数为：

(10)

因此，对数似然p(u(1,2,…,l))的偏导数为：

(11)

式中：偏导数U是一个O×N的矩阵，噪音方差σ2可以从原始序列和模型预测输出中估计得出。给定两个时间序列ui和uj，计算出序列对应的生成函数模型的偏导数Uui和Uuj，Fisher核度量可以通过式(5)获得。Fisher核认为同类样本若能够以相同的方式“拉伸”生成模型的参数，表明这两个样本在给定的参数模型上具有某种相似性，用这种相似性来度量原始时序样本的距离。

2.2 基于Fisher核的时间序列集成算法

假设给定包含M个时间序列样本的训练集S={u1,u2,…,uM}，图2描绘了模型的结构。

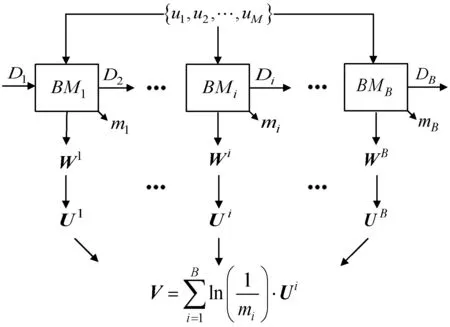
图2 算法的集成训练过程

对于第i个ESN基模型BMi而言，为每条时间序列学习出一个函数模型，得到对应的训练误差以及模型的读出映射，Di表示样本的权重，Wi是第i个基模型在全部训练样本上获得的读出映射矩阵，根据训练每个样本所产生的误差，我们可以计算出第i个基模型在本轮训练的回归误差ei，根据回归误差和样本的权重，可以计算出第i个基模型的权重mi以及更新样本下一轮的权重Di+1。Ui表示第i个基模型为全部训练样本学习出的费希尔分数矩阵，矩阵的每一行表示一个样本所对应的费希尔分数向量。依次进行，最终获得B个基模型。在训练过程中，上一轮被错分的样本的权重将会增加，被正确分类的样本的权重将会降低，更新权重后的样本将会被用于下一轮的训练，下一轮的基模型将会更加关注那些错分的时序样本。获得每个基模型学习到的费希尔分数矩阵之后，本文重新计算了一个新的费希尔分数矩阵，此矩阵的每一行是每个基模型学习到的费希尔分数矩阵对应行的加权和，即：

(12)

式中：Vj表示针对时序样本uj所训练出的集成费希尔分数向量。得到最终的费希尔分数向量之后，可以根据式(5)计算出对应的Fisher核矩阵，采用SVM核方法来完成分类任务。算法1描述了整个训练过程的细节。

算法1基于集成回声状态网络的Fisher核学习

1. 输入：时间序列数据集S，储蓄池尺寸N，岭回归参数λ，基模型个数B

2. 输出：Fisher核矩阵

3. 初始化时序样本权重

4.D1={sw11,sw12,…,sw1M},sw1k=1/M

5. fori=1 toBdo

6. 生成一个弱的分类器BMi，从带权重的时序样本集中学习出读出映射Wi

7. 统计出训练样本上的最大误差Ek=max(NMSEk)，NMSEk是拟合第k个样本所产生的归一化的均值平方误差

8. 计算每个样本的相对误差

9.eik=NMSEk/Ek,k=1,2,…,M

10. 计算基模型的回归误差

12. 获得基模型的权重

14. 更新样本权重分布

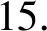
16. 通过式(11)计算出费希尔分数矩阵

17. end for

18. 获得每个样本的加权和的费希尔分数表示

20. 计算出Fisher核矩阵，矩阵中的每个元素通过式(5)得出

3 实 验

本节首先在人工合成数据集上验证了FKIESN具有一定的鲁棒性，其次在时间序列基准数据上与其他基线模型进行了性能对比实验，相关的参数分析实验在本节的最后给出。

3.1 实验设置

本节采用的对比算法有：基于欧氏距离的最近邻算法(ED)[14]、最大间隔最近邻(LMNN)[4]、基于动态时间规整的最近邻算法(DTW)[6]、词袋模型(TSBF)[7]、基于shapelet转型算法(ST)[8]、基于储蓄池的核方法(RV)[15]和基于费希尔储蓄池的核方法(FisherRV)[18]。在RV和FisherRV中，核宽度γ通过5折交叉验证选择，搜索范围为{10-5,10-4,…,101}，岭回归超参数λ的搜索范围为{10-5,10-4,…,101}。为防止过拟合，FKIESN中基模型水库大小最优设置为5，基模型个数设置为10。本文采用LIBSVM工具包中的SVM算法来进行分类任务，一对一策略用来解决多分类任务，通过交叉验证在{10-3,10-2,…,103}范围内选择出最优的正则化参数C。在训练集上使用交叉验证选择模型后，将所选模型在整个训练集上重新训练一次，并在测试集上进行评估。

3.2 鲁棒性分析

首先利用非线性自回归滑动平均(Nonlinear Autoregressive Moving Average,NARMA)系统[22]生成10、20和30阶的时间序列，产生公式如下：

1.5u(t-9)u(t)+0.1

(13)

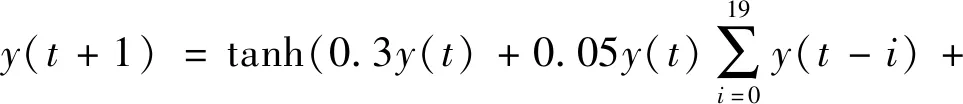
1.5u(t-19)u(t)+0.01)+0.2

(14)

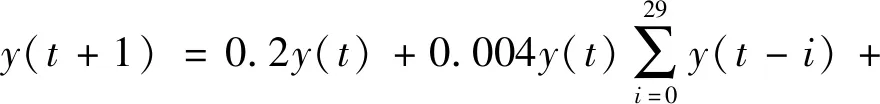
1.5u(t-29)u(t)+0.201

(15)

式中：y(t)和u(t)分别是当前时刻的输出和输入。这三种序列从相同的输入u中产生，u是从[0,0.5]区间上均匀随机产生，三类序列的产生长度都是80 000，图3描绘了三类不同的NARMA序列。每条序列被分割成100条长度为800的子序列，每种类别的50条子序列分到训练集，剩下的50条分到测试集，最终获得大小都是150条子序列的训练集和测试集。向这些数据集中添加高斯白噪声，噪声的均值为零，方差分别为0.1、0.2、0.3、0.4、0.5}。这样设置的目的是可以清楚地显示模型的性能变化趋势。实验中，对于每个噪音级别，生成合成序列5次，每次在合成数据集上重复10次实验，将平均分类准确度作为最终的评估结果。图4展示了实验的最终结果。

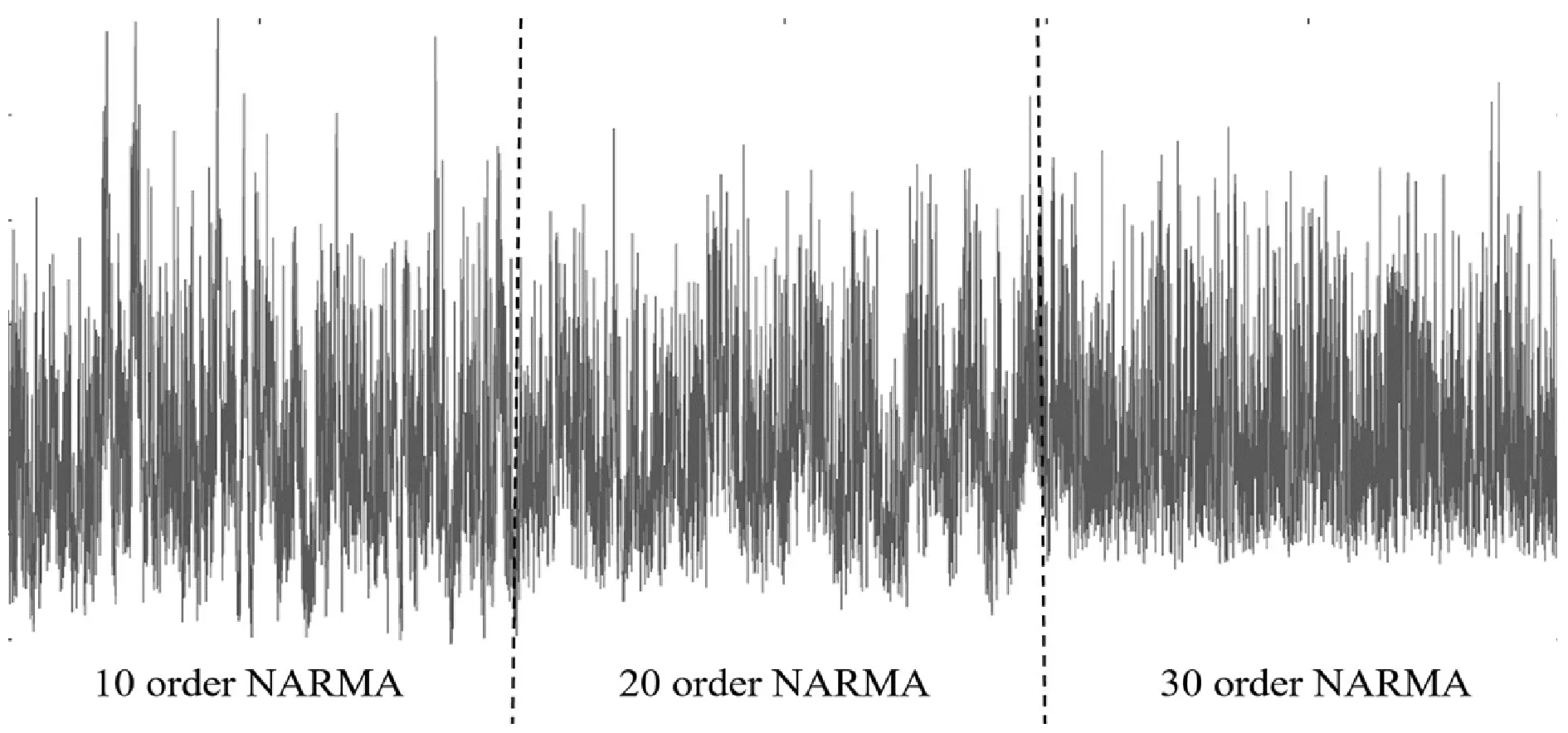
图3 三种类别的NARMA时间序列(10、20和30)

图4 模型在不同噪音级别下的分类错误率

可以看出，与对比算法相比，FKIESN对噪音更具鲁棒性。DTW对噪音比较敏感的原因是它本质上还是基于点与点的比较，这将导致它对序列的形状有很强的依赖，然而，高斯噪音的加入改变了原始序列的变化幅度，使得DTW的分类性能受到较大的影响。RV将原始序列从数据空间映射到模型空间中，适当地降低了噪音带来的影响，在噪音数据集上获得了仅次于FKIESN的分类性能。FKIESN不仅采用Fisher核在模型空间中合适地度量函数模型之间的距离，还引入AdaBoost训练出多个基模型来拟合数据复杂的分布结构，进一步降低了噪音的影响。

3.3 分类性能比较

本文在12个来自UCR[23]的时间序列基准数据集上比较FKIESN和其他基线模型的分类性能，数据集都被分割成训练集和测试集，详细信息如表1所示。

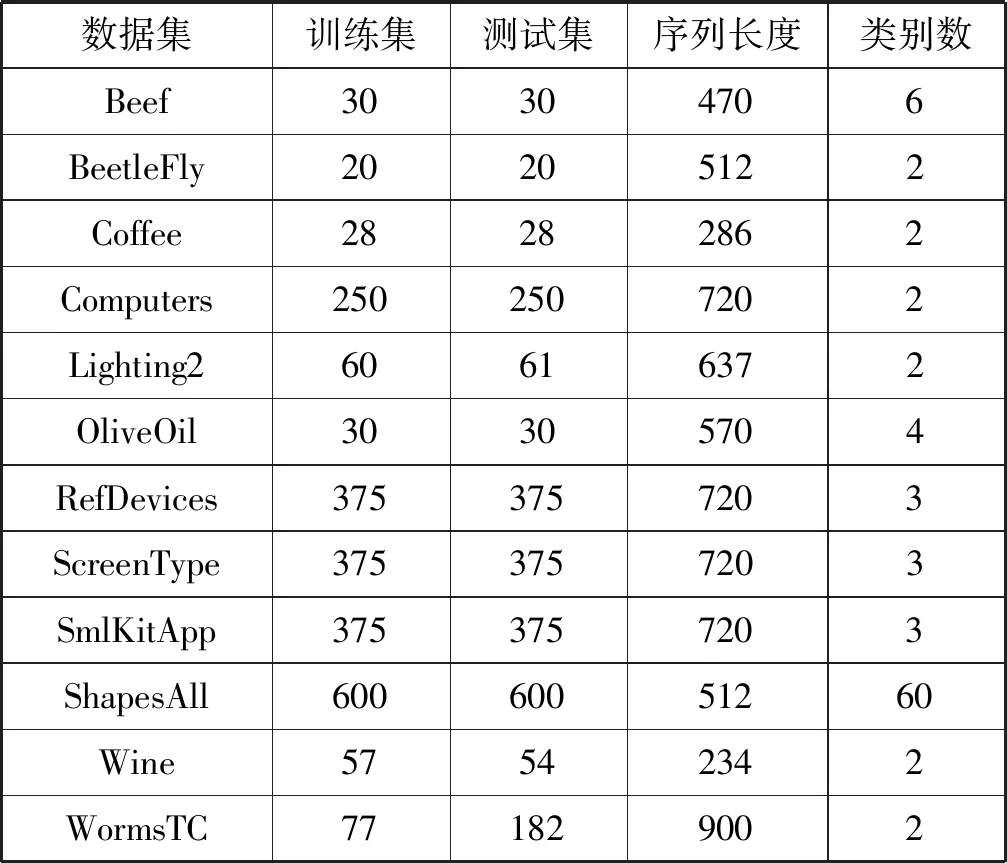
表1 12个UCR时间序列基准数据集的详细信息

实验结果如表2所示，在每个数据集上，可以看出FKIESN在大部分数据集上优于其他基线模型。具体而言，FKIESN在9个数据集上比基于距离的方法和基于模型的方法表现出色，同时在大部分数据集上优于基于特征的方法。隐藏在长序列中的模式信息通常很难捕捉，值得一提的是，对于长序列数据集，比如RefDevices、SmlKitApp和WormsTC，本文算法与其他对比算法相比仍旧有比较低的分类错误率，原因可能在于本文使用多个模型捕捉长序列中的复杂模式。对于每个数据集，本文将8个算法进行排序，具有最小分类错误率的算法获得名次1，以此类推，具有最大分类错误率的算法则获得名次8，具有相同分类错误率的算法获得相同的名次，然后统计各个算法在12个数据集上的平均排名，如表2倒数第二行所示，可以看出FKIESN在平均排名上明显地优于其他算法，ED则获得了最差的平均排名。考虑到平均排名评价准则是一种无偏的度量方法，对模型池的选择和大小很敏感，本文采用一种更加鲁棒的评价准则[24]：

(16)

(17)

式中：ek和ck分别代表模型i在数据集k上的分类错误率以及数据集包含的类别数量，数据集上每种类别的误差用PCEk表示，MPCEk表示模型在所有数据集上的平均每种类别的误差。表2的最后一行给出了最终的计算结果。可以看出，FKIESN在MPCE上表现优异，基于模型的方法RV和FisherRV次之，基于距离的两个算法(DTW和LMNN)与基于特征的两个算法在MPCE上性能相当，ED算法还是表现最差。

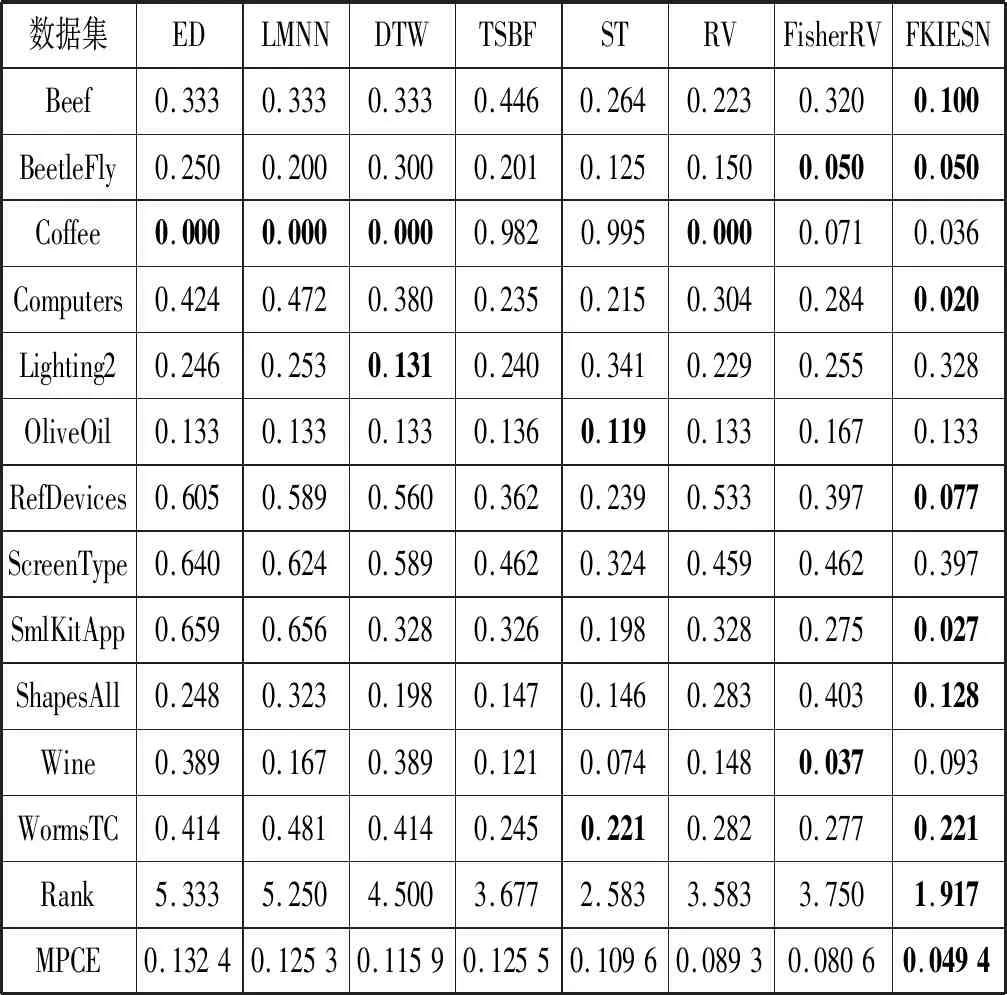
表2 FKIESN与对比算法在12个基准数据集上的分类错误率

3.4 相关参数分析

当储蓄池神经元数量设置太大时，经典的ESN模型会出现过度拟合的现象，本节将探究储蓄池大小对FKIESN分类性能的影响。实验中，保持其他参数不变，改变储蓄池规模的大小，改变范围为N∈{5,10,20,30,40,50,60,70,80,90,100}。对于特定的储蓄池规模，在每个数据集上重复做20次实验，取20次实验结果的平均值作为最终的结果。图5展示了模型在Beef和BeetleFly两个时间序列基准数据集上的表现。

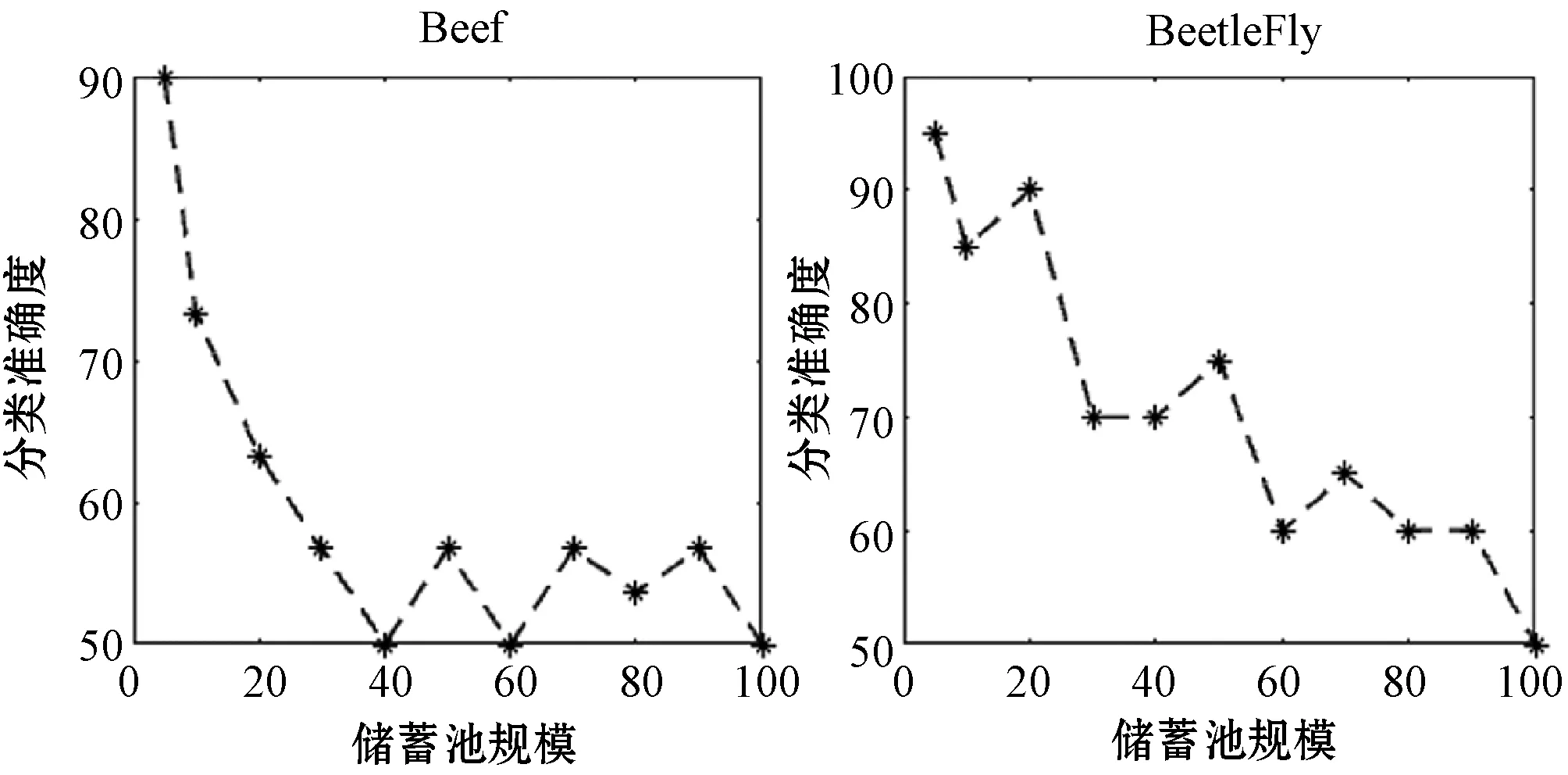
图5 不同储蓄池规模对模型分类准确度的影响

可以看出，储蓄池大小对模型产生很大的影响，随着储蓄池神经元的增多，模型在数据集上的分类性能总体呈现下降趋势。储蓄池神经元的增多，导致基模型的拟合能力增强，这与AdaBoost集成学习要求基模型是一个弱分类器的事实相违背，多个过强的基模型提取过多的冗余信息，反而导致模型的分类性能下降。

4 结 语

本文基于回声状态网络和Fisher核，提出了一种时间序列集成模型FKIESN。基于回声状态网络的Fisher核在模型空间中度量函数模型之间的差异，同时在特征层面上引入AdaBoost集成，利用多个模型来拟合数据复杂的分布结构，提高了算法的分类性能。除此之外，FKIESN是基于回声状态网络生成模型，它很自然地解决了时间序列变长问题以及能捕捉序列中的动态信息，不仅在大多数时间序列基准数据集上优于对比的基线模型，也在人工合成数据集上表现出较好的鲁棒性。

本文提出的框架具有开放性，未来将在模型空间中继续探索其他有效的距离度量方式，提高模型的分类性能，同时针对海量序列样本且序列比较长的分类问题，在保证分类性能的同时，加快模型的分类速度。