基于光流的六旋翼飞行器的控制系统研究

刘祚时 饶 远

(江西理工大学机电工程学院 江西 赣州 341000)

0 引 言

随着微电子机械系统(MEMS)技术的飞速发展，微型控制系统的整体体积越来越小，这为机械构件、驱动部件、光学系统、电控系统以及数字处理系统集成在一个微型的整体单元上提供了技术基础。在这样的技术条件下，有关无人机的相关研究也逐渐增多，但由于飞行器的控制系统作为一个多输入输出的非线性系统，具有多变量、强耦合的特点，因此经典的控制算法已经无法适用于飞行器的时变非线性控制系统。其中光流技术作为一项成熟技术，已经在多旋翼飞行器上被大量应用。例如：国外的部分学者将光流技术用在无人机的姿态估计恢复[1]或无人机降落及其地貌跟踪[2]等研究上；国内的部分科研机构则是利用光流实现了目标跟踪[3]、自主悬停[4]、运动小目标检测[5]等功能。郭力等[6]提出了一种在无人机上装载单目摄像机来实现目标点定位的方法，但由于该方法在小范围空间内使用时定位偏移误差较大，不适用于低空环境下。吕强等[7]采用最小绝对误差和块匹配(SAD)算法来求解机身相对与大地坐标系的水平速度，但存在位置估计精度低的问题，且SAD匹配法易受外界光照强度的影响会导致光流传感器定位精度变差。李亚斌[8]提出的基于VOD块匹配准则的连续消除算法(SEA)能够有效地避免光流传感器受外界光照强度变化的影响，但是为了采集到更加完整连续的光流信息，其利用多个相机采集光流信号导致控制器处理数据的时间过长，进而降低了控制系统的实时性。

本文提出一种利用光流模块提取目标点所在平面的平移光流并设计相应的外部控制回路，同时结合内部姿态角速度控制回路，实时获取飞行器水平速度及其高度信息，并将光流信息作为控制系统的反馈信号，有效提高飞行器控制系统的定位精度。

1 建立飞行器数学模型

1.1 实验平台

本文采用PX4Flow光流模块，并在此基础上对六旋翼飞行器进行整机搭建，其实物图如图1所示。

图1 飞行器实物图

在飞行器飞行过程中，可通过PX4Flow光流模块对地面的光流信息进行采集。随后飞控系统将光流模块采集的光流信息通过数传发送至PC端，其中数传发送数据时按照MAVLink协议进行实时通信，从而便可从上位机软件QGC(QGroundControl)中观测飞行器在飞行过程中的光流信息的实际变化情况。图2为实验系统整体架构图。

图2 实验系统整体架构图

1.2 飞行器动力学分析

依照六旋翼飞行器的整体结构建立空间直角坐标系，以机架几何中心点O为坐标原点，电机4底座和电机6底座之间远离点O的角平分线方向作为x轴，垂直于x轴并通过电机1底座中心的方向为y轴，故可由右手定则确定z轴的正方向。而图中标注的F1至F6分别为各自所对应的电机产生的输出力，其方向规定为与坐标轴同向为正，并且电机1、3、6顺时针转动，电机2、4、5逆时针转动，如图3所示。

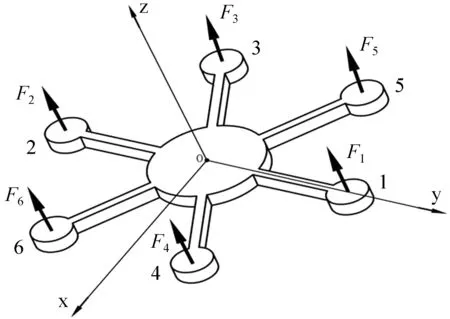
图3 六旋翼机架结构图

为了能够简化飞行器的数学模型，并且便于后续的运动分析，现根据六旋翼飞行器的系统结构特点做出下列假设：(1) 假定飞行器是理想状态下的刚体，其几何中心点与重心点相重合；(2) 将飞行器整体所受的升力视为线性的，同时螺旋桨正反转产生的力大小相等，并忽略飞行器正反桨到达所需转速的时间；(3) 当飞行器处于静止平衡状态时，整体的重心处于z轴(偏航轴)上，同时飞行器的姿态角全为零(即俯仰角、横滚角和偏航角为0)，并且忽略摩擦力与阻尼力矩。

在上述假设条件的基础上，分析飞行器各姿态角方向的力矩平衡模型。

(1) 俯仰角的力矩平衡模型。针对六旋翼飞行器绕y轴转动即俯仰角方向，进行平衡受力分析。由于此时电机1、2的升力F1、F2在xoz的投影通过点O，故不考虑其对俯仰运动的影响。如图4所示。

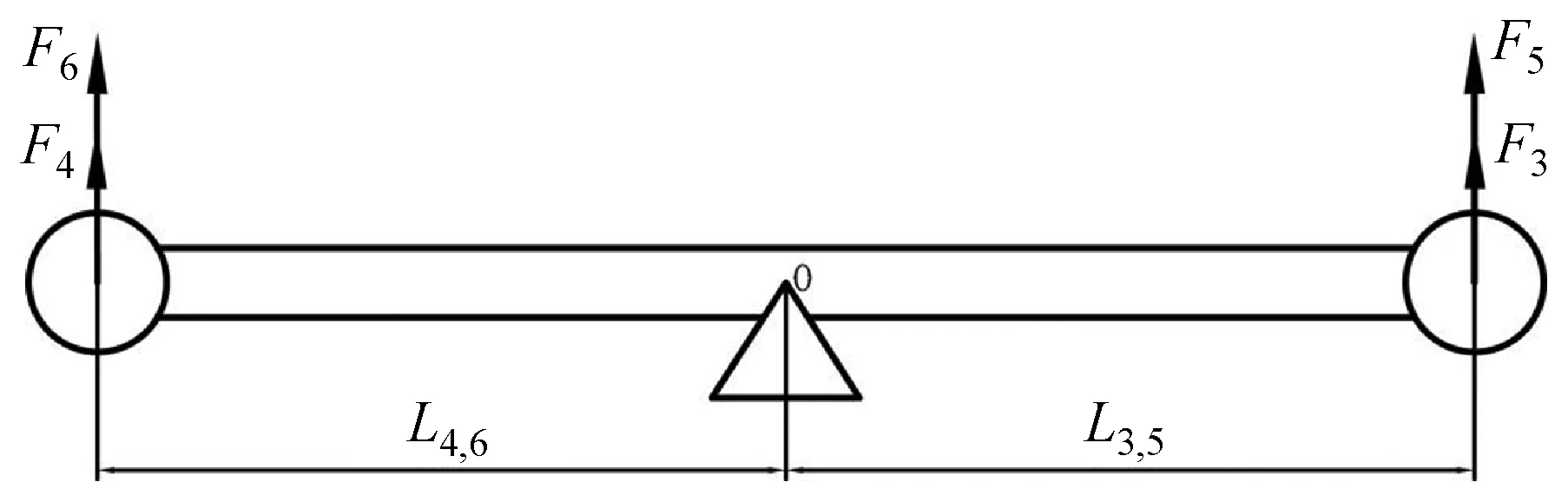
图4 俯仰角受力分析图

当飞行器在做俯仰运动时，电机1和电机2的输出升力为正且方向与z轴平行，现选取电机4和电机6的向下运动的方向为俯仰角的正方向，其中飞行器机架上电机轴心到机架重心点的距离为L，则有如下方程：

(1)

L3,5=L4,6=Lcosθ1

Fi=KscUii=3,4,5,6

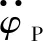
故可得：

(2)

(2) 横滚角的力矩平衡模型。针对六旋翼飞行器绕x轴转动即横滚角方向，进行平衡受力分析，如图5所示。

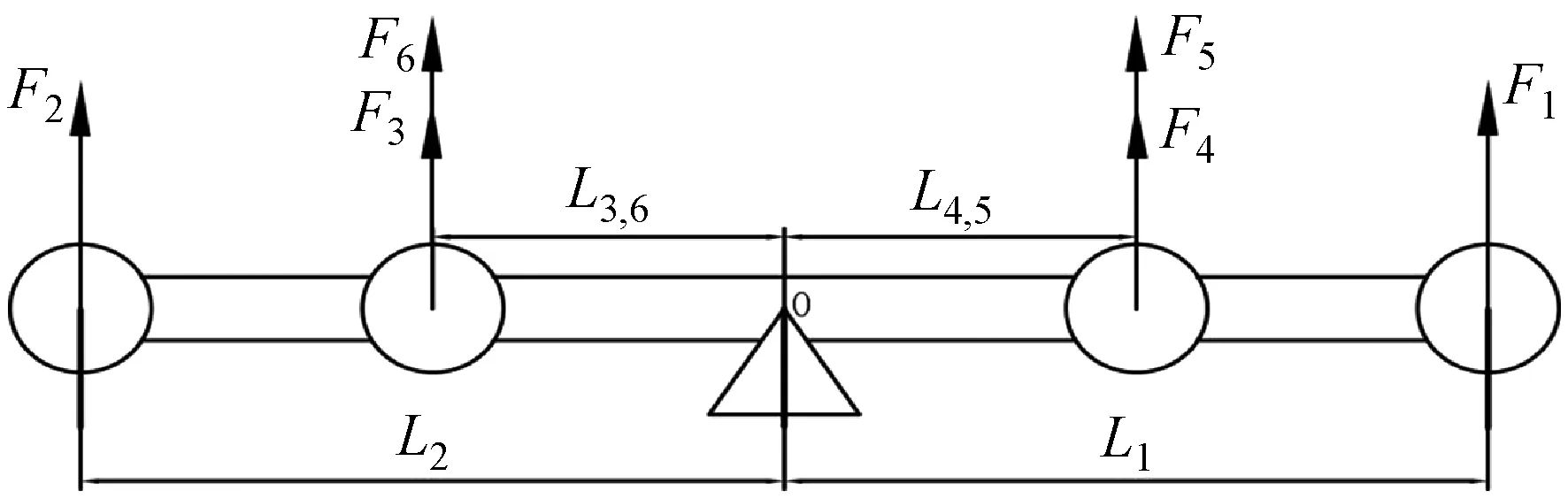
图5 横滚角受力分析图

当飞行器在做横滚运动时，选取电机2向上运动的方向为横滚角的正方向，则有如下方程：

(3)

L1=L2=LL3,6=L4,5=Lcosθ2

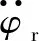
由此可得：

U4cosθ2-U5cosθ2)

(4)

(3) 偏航角的力矩平衡模型。当飞行器在做偏航运动时，选取绕z轴逆时针转动的方向为正，则有：

(5)

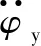
(6)

将飞行器各结构部分简化并视作质点时，由式(2)、式(4)、式(6)可知转动惯量分别为：

(7)

同时得到姿态角的力矩平衡方程为：

(8)

1.3 建立飞行器状态方程

由式(8)可知各姿态角输出与输入电压之间的关系，考虑到姿态角(主要为横滚角与俯仰角)之间的耦合关系，对其进行解耦处理。现定义五个输入变量Vi(i=1,2,3,4,5)，V=[V1,V2,V3,V4,V5]T，并满足以下条件：

(9)

通过式(9)的分配关系来确定输入的控制量，同时选定九个系统状态变量建立空间状态方程：

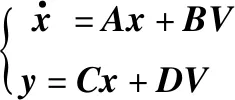
(10)

式(10)中的系数矩阵为：

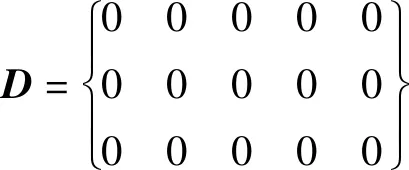
对六旋翼飞行器实际参数的测量，各项具体参数如表1所示。

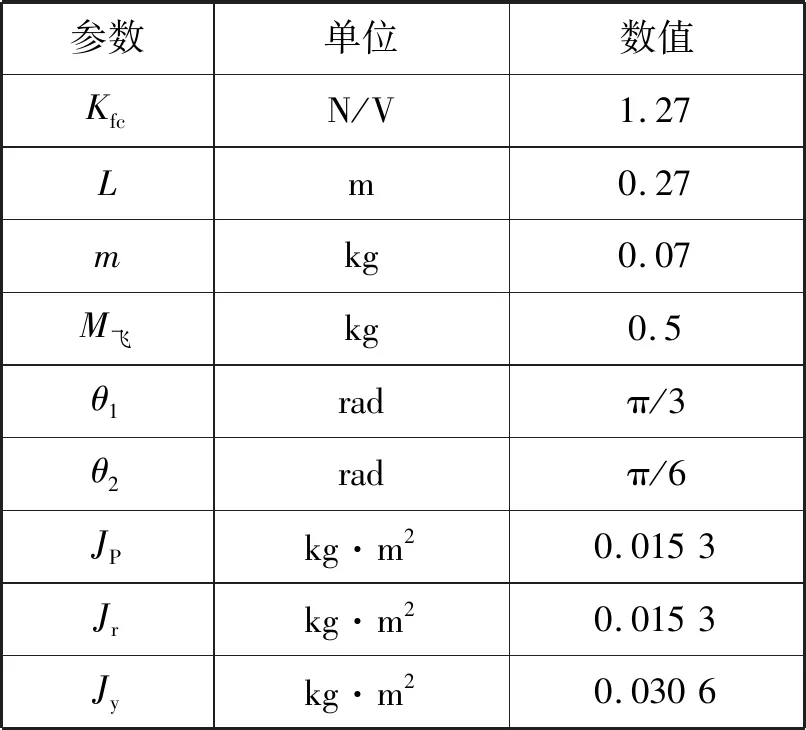
表1 六旋翼飞行器参数

2 获取光流信息

为了确定飞行器与地面之间的位姿关系，现规定大地坐标系G和飞行器坐标系F，则飞行器在大地坐标系中的位置为：η=[X,Y,Z],而飞行器绕飞行器坐标系转动的姿态角(偏航角，俯仰角，横滚角)可表示为：ζ=[α，β，γ]T。因此，可定义飞行器坐标系相对于大地坐标系的转动角速度在其自身各轴上的投影为σ=[σ1，σ2，σ3]T，并假设光流模块安装在飞行器的重心点处，同时PX4Flow光流相机的镜头焦距为16 mm。

2.1 目标点与镜头的映射关系

目标点动态映射如图6所示。其中点N为三维空间内的静止目标点，其坐标为(X,Y,Z)∈R3,该点映射至球面镜头上的点Ms处，P2为镜头捕获光流的窗口曲面，v为飞行器质心相对于地面的平移速度，σ为飞行器绕飞行器坐标系F转动的角速度，S2为球面镜头曲面。因此可知映射关系为：

(11)

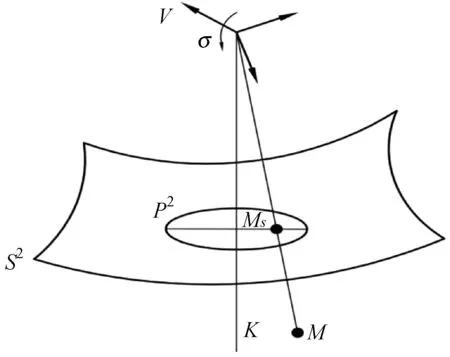
图6 目标点动态映射图

由于目标点相对大地坐标系而言处于静止状态，所以当镜头捕捉到目标点的水平运动时，即表示飞行器在相对目标点发生位置移动。因此，从目标点至镜头曲面的映射半径可表示为[9]：

(12)

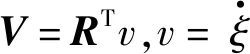
(13)

(14)

式中：K的正方向为图6中竖直向下的惯性方向；μ为目标点映射到镜头曲面上的夹角。

2.2 水平移动光流的获取

(15)

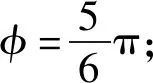
(16)

(17)

3 系统控制器的设计

本文利用LQR(线性二次型)内控制回路在飞行器通过外部光流控制回路进行定点飞行，有效避免光流传感器受到外界光照强度变化(比如在环境光照强度较差或地面反光严重的情况)的影响，以此实现六旋翼飞行器在环境照明条件较差或强光情况下的光流定点的稳定姿态控制[10]。

3.1 内部姿态角速度控制回路的设计

当飞行器控制系统的状态方程简化为线性系统状态方程时，LQR作为适用于线性系统最优化控制的方法，可通过确定飞行器的系统状态变量及其被控输入变量所构成的二次型函数来作为衡量系统是否达到了最优化控制的稳定状态。同时求解出该二次型积分函数的最小值，使其控制系统达到最优控制状态，完成最优化控制器模型的设计[11]。

本文将采用LQR控制方法来实现内部姿态角速度控制回路的设计，即分别针对三个姿态角速度(横滚角速度、俯仰角速度以及偏航角速度)设计相应的LQR内回路控制器。在这个控制过程中将系统的状态变量输入内回路后所产生的误差视为新的变量，并把新变量作为输入信号再次输入该控制回路。因此，可通过这样的方式消除该内控制回路中引入系统状态变量时所带来的误差[12]，达到提高系统实时性、精确跟踪输入变量的目的。

由于在内部控制回路中重新将误差变量e引入进系统控制回路，故设参照输入变量为j，其有待持续观测的输出变量为p，并满足p=Ccx，则误差变量为e=j-p，结合式(10)得到新的系统状态空间表达式：

(18)

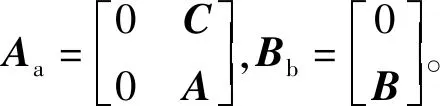
(19)

式中：W和M都为半正定阵；R为正定阵；t1为固定的终端时间，且系统终端状态z(t1)自由；W为系统状态变量的加权矩阵；M为输入向量的加权矩阵。因此只需保证性能函数最小，就能得到输入信号的最优控制状态，所以先构造一个与性能指标函数相关的Hamilton函数。

(20)

当不对输入变量进行限制时，对式(20)求导，则有：

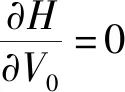
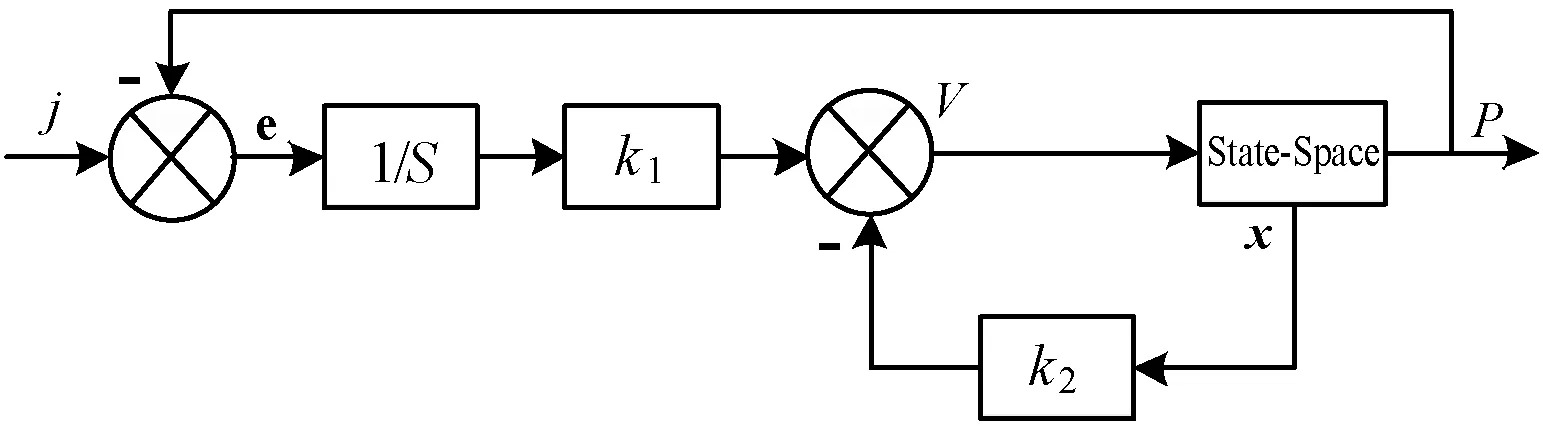
图7 内回路控制框图

故可知最佳输入信号应为：

(21)

所以在进行内控制回路的设计时，要选取合适的加权矩阵W和R来保证控制系统的整体性能，即当需要系统有良好的输出性能时，应将W主对角线上的系数调高，倘若需要降低系统输出信号时，则应将R的参数调高。当选取的加权矩阵W和R能够较好地平衡输出信号与输出性能时，就实现了系统的最优化控制。此时，在确定了矩阵A、B和C及其加权矩阵W、R的前提下，可通过MATLAB求解出全状态反馈增益矩阵K。

3.2 外部光流控制回路的设计

本文在利用LQR实现内部姿态角速度控制的基础上，采用PI控制器对光流信号进行调节控制，以实现飞行器的悬停控制。由第2节的内容可知λ和d(t)/ds0是可计算量，故结合式(16)和式(17)可知稳定悬停状态下飞行器的动力学方程为[9]：

(22)

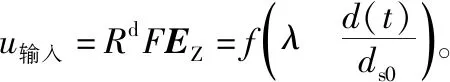
(23)

式中：kP、kI都大于0，Rd表示预期飞行器飞行的方向；F表示飞行器的升力；EZ表示大小为[0,0,1]T的列向量；FG表示飞行器的重力；Δ表示为外界施加给飞行器的干扰力。因此可知飞行器的线速度v趋向于0。当目标点所处的平面位于大地坐标系的水平面(xoy)上，且飞行器的期望方向与xoy平面平行时，飞行器在稳定悬停的状态下，可认为目标点到飞行器坐标系的正交距离d，即为光流镜头到目标点所处目标平面的高度，这时PI控制器的闭环控制可简化为：

(24)

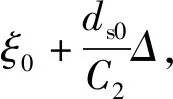
4 实验过程及其结果

在进行实验前对飞行器定点飞行的稳定性进行了相关的分析验证，同时对本次实验的各项参数进行设定。其中光流镜头可观测的范围为80°，飞行器实验时飞行高度为1 m，外回路光流PI控制器中kP、kI分别为1.05、0.32，飞行器前向速度1.2 m/s，光流模块采样频率25 Hz。假设实验时飞行器的最大偏移量为12 cm，各姿态角的误差在±3°内，而偏移速度为1.6 m/s。实验采用类比法对实验结果进行比对，并采用Lucas-Kanade方法估算光流。

4.1 实验1

进行实验1前，需用镜头盖遮挡住光流镜头，其目的是为了模拟在实验地面上无可识别目标点的定位情况，同时选取纹理清晰的大理石地面作为飞行器试飞地面即目标点所处平面。由图8和图9中的飞行器的轨迹信息与光流信息可知，在遮挡光流的情况下飞行器的漂移轨迹范围较大，其偏移量几乎达到了允许偏移量的最大值，且飞行器在xoy平面上的偏移方向不确定，但在z轴方向上的位移量大致为±4 cm。就整体而言，飞行器在内姿态角速度回路的控制下，其漂移轨迹都在预设边界的内部，即表明无人机悬停的位置在允许范围内。同时可以看出飞行器位置的偏移变化大致与各轴的光流变化趋势一致。因此，实验1充分验证了内控制回路的可行性。

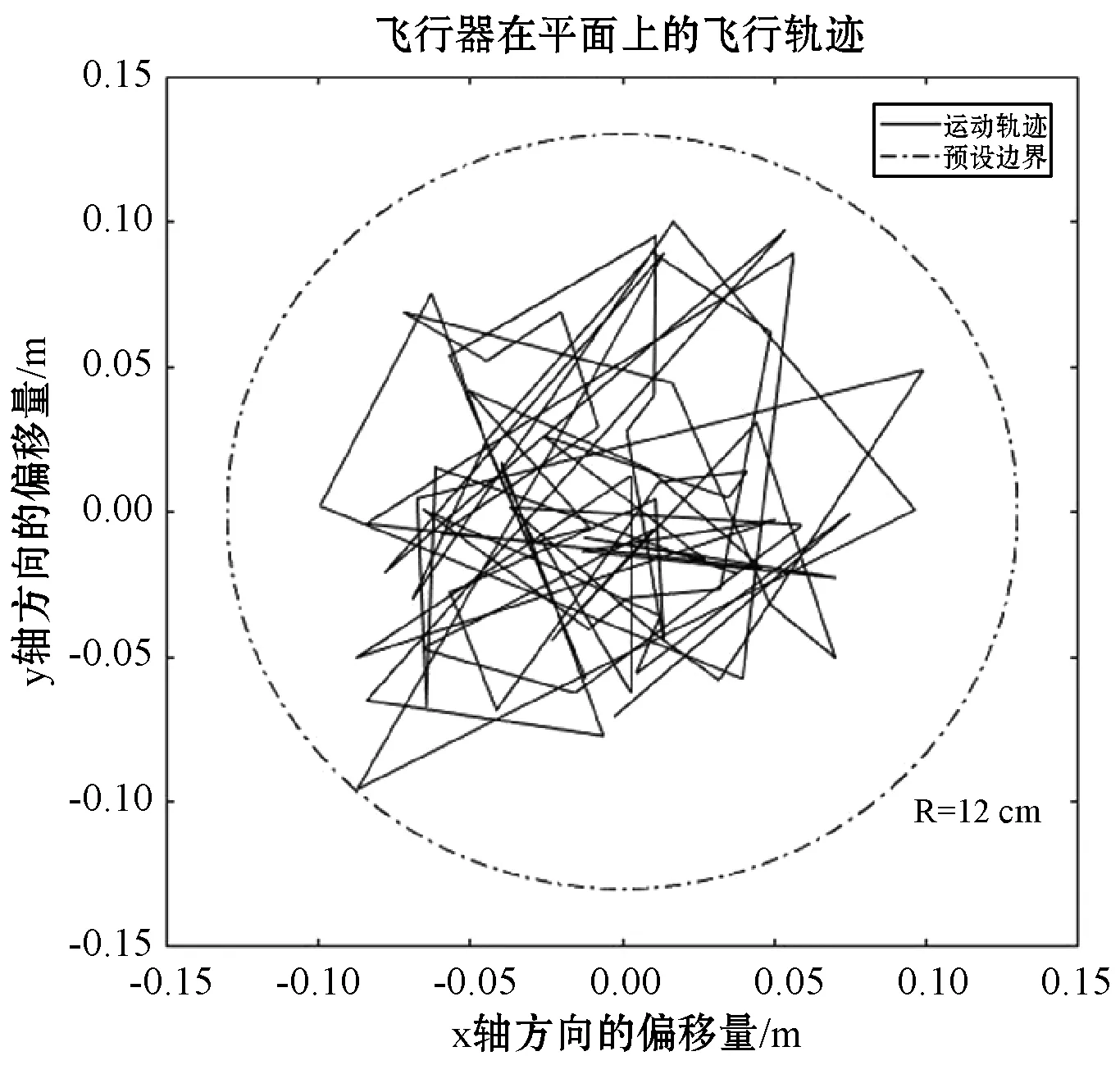
图8 飞行器飞行轨迹

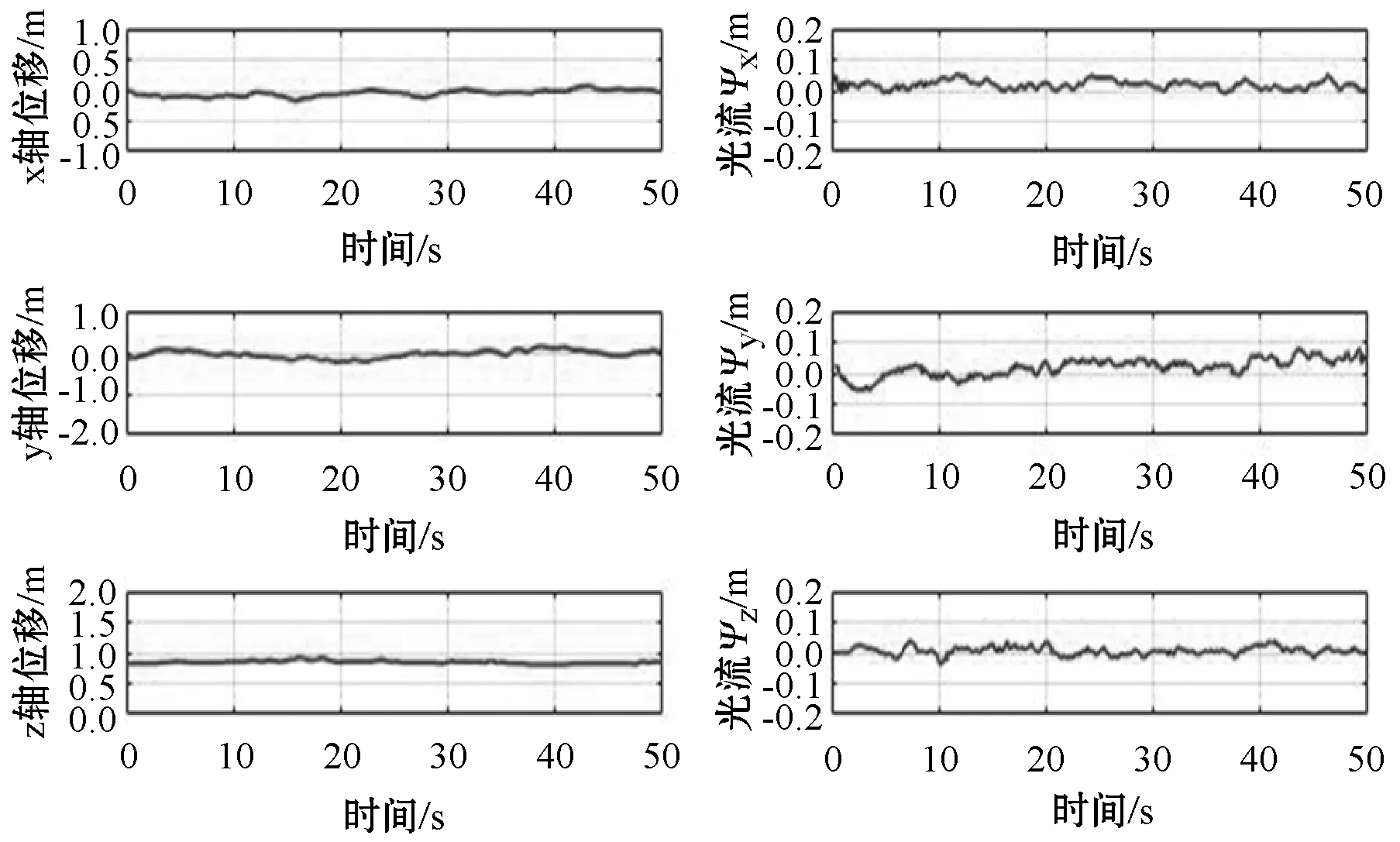
图9 实际位置与对应光流

4.2 实验2

进行实验2前，将镜头盖取下保证光流镜头不被遮挡，且处于正常工作状态。飞行器轨迹信息与光流信息如图10和图11所示。可以看出：虽然光流在某个时间段变化剧烈，但整体上都在远小于±0.1的范围，故可认为光流趋于0且变化稳定；而z轴的位置变化量在±3 cm范围内，x、y轴的位置偏移量也在±3 cm内。所以，各轴所对应的光流变化趋势都与相应的各轴位置偏移大致保持一致。因此，实验2在实验1的基础上充分证明了外控制回路的可行性，同时也验证了本文提出的内、外回路控制方法是有效的。

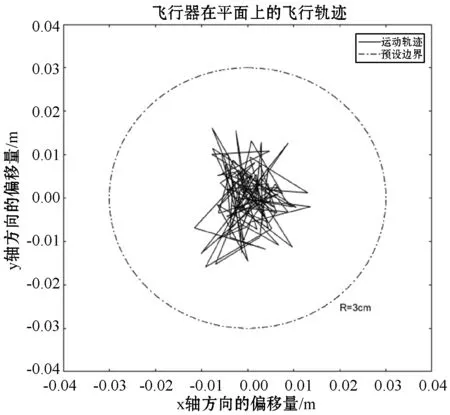
图10 飞行器飞行轨迹

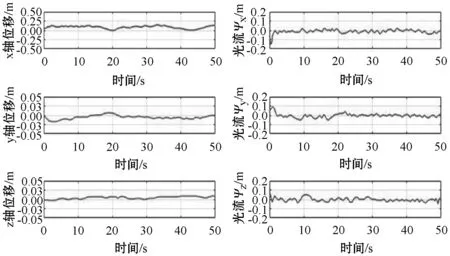
图11 实际位置与对应光流

实验1的实验结果表明在遮挡光流的情况下，由于光流无法正常工作致使飞行器无法获取光流数据，进而导致外部控制回路的失效。虽然飞行器能够在预设边界内正常飞行，但此时飞行器的水平飞行轨迹漂移量较大，且漂移方向不明确。而实验2则是在光流正常工作的情况下进行，当前向速度保持不变时，飞行器各轴位置及其各轴所对应的光流值都趋近于预想期望值，且飞行器在±3 cm的水平方向范围内稳定飞行，同时在z轴方向上的偏移量也为±3 cm。表2为20组飞行实验的统计结果，其中各项数据都以平均值±标准差来表示。

表2 实验数据统计

4.3 实验实时控制分析

由式(6)中六旋翼飞行器的状态空间模型，可提取相关参数，并令其增益矩阵Kp、Kr和Ky分别为：Kp=[1.54,2.30]，Kr=[0.83,1.28]，Ky=[0.62,1.03]。而针对俯仰角、横滚角和偏航角的PI控制器其比例系数为1.35、1.51、1.70，积分系数为0.24、0.29、0.33。故由本文提出的双回路非线性控制器的方法，可得其姿态角速度的阶跃响应，如图12所示。

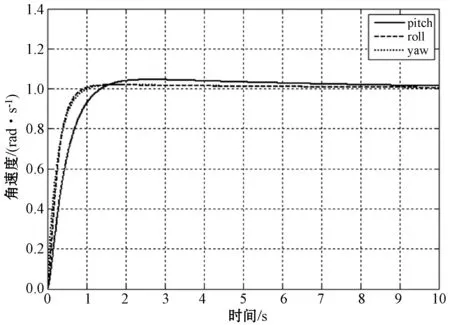
图12 姿态角速度阶跃响应

由此可知，本文提出的控制方法能够较快地跟上输入量且超调量较小，可达到较为理想的控制效果。同时由LQR控制的特点可知，对内部姿态角速度的干扰输入，系统将把该误差作为状态变量，使姿态角速度响应能够快速到达目标点位置，且该调整过程中实时性较为理想，在3 s内即可完成飞行器的稳定定点。

5 结 语

本文提出了一种应用双回路非线性控制器的方法，结合外部光流PI控制回路和内部姿态角速度LQR控制回路，实现了飞行器定点悬停任务。实验结果表明当光流失效时，飞行器的漂移范围较大且漂移方向未知，同时z轴方向上的偏移量在±4 cm范围内，此时飞行器仍在预设边界的范围内正常飞行，但定点效果较差。而在光流正常工作时，其平均误差在0.04±0.03 m范围内，而水平方向上的偏移量和z轴方向上的偏移量都在±3 cm内，此时飞行器定点精度较为理想。