一种基于语义轨迹的相似性连接查询算法
2020-07-13高祎晴
高祎晴 潘 晓* 吴 雷,2
1(石家庄铁道大学经济管理学院 河北 石家庄 050043)2(燕山大学信息科学与工程学院 河北 秦皇岛 066004)
0 引 言
随着全球定位系统和无线通信系统的发展,配备GPS的移动设备不断涌现(例如车辆导航系统和智能手机),基于地图的在线服务不断扩散(例如Google Maps2和MapQuest3),轨迹数据在当下的大数据时代扮演着越来越重要的角色。常见的轨迹数据[5],除了GPS设备采集到的人或车辆等运动物体的移动路线以外,还包括传感器采集到的数值随时间的变化情况,比如某个监控对象的温度和湿度变化曲线也可以认为是温度和湿度所构成的二维空间中的一条轨迹。因此可以说轨迹无处不在,这些丰富的轨迹数据资源也带来了对于轨迹数据研究的巨大需求。目前对于轨迹数据的研究,大部分集中于对于轨迹数据的查询和清洗[14],受现有存储能力和计算能力的限制,非常有必要对轨迹规模进行缩减。那么当轨迹集合中的部分轨迹表现相似,那么便可以删掉其他相似轨迹只留其一条。因此对于轨迹相似性查询的研究成为了一个热点问题。即用户给定一个相似值,就可以在一个轨迹数据集中查找出满足用户要求相似性的轨迹对,并返回给用户[9]。
空间相似性查询是轨迹相似性查询中较为普遍的一种操作方式,基于空间角度对轨迹进行相似性的衡量,根据用户给定的相似性阈值,对于查询轨迹集中的轨迹进行相似性度量,找出满足用户要求的空间相似性阈值的轨迹对,并且返回给用户。目前越来越多的应用中出现了地理位置与文本信息交融的现象[8]。一方面,越来越多的场所,例如商店、饭店、游乐场等,都附加了与其地理位置相关的文本描述信息;另一方面,文本信息也通过地名、街道、地址等特征与地理信息相关联。所以如果仅考虑空间这一方面的相似性,可能对于轨迹相似性衡量较为片面。因此,本文在相似性的度量方面融入了文本信息的考虑,综合了空间和文本两方面对于轨迹的相似性进行衡量[12]。例如,当A用户在A省找到与其相似性满足要求的轨迹t时,如果轨迹t的用户出现在B省,恰好A用户也想去B省,那么当给其推荐轨迹时,就可以参考轨迹t的用户在B省的轨迹推荐给用户A。在衡量相似性时,如果只考虑空间方面也就是距离问题,就显得不够严谨[4]。针对根据相似性向用户推荐可行路线,除了考虑距离问题即空间方面外,也应该考虑关键字的问题,由此推荐的轨迹能够更加符合用户的要求[7]。
以图1为例,在所调查的空间中有三条轨迹t1{p11,p12,p13}、t2{p21,p22,p23}、t3{p31,p32,p33},假设t1为查询轨迹,t2、t3为被查询轨迹。当只考虑空间因素时,可以轻易地得到t2相较t3与t1更为相似。但是当考虑空间和文本两个方面时,根据表1中轨迹的详细信息,轨迹t3和t1的相似性要大于轨迹t2与t1的相似性,所以会更容易满足用户的要求。因此,对于两条轨迹相似性的度量,除了考虑轨迹间的距离外,还要看关键字的匹配程度。

图1 轨迹相似性示例
之前的研究者针对相似性研究方面提出了许多索引技术和查询算法[6]。本文通过对空间相似性和文本相似性赋予不同的权重,找到空间方面的边界值,或者是文本方面的边界值。根据这个边界值在空间和文本方面进行范围查询,通过计算出来的范围去除一些不必要的轨迹,进而缩小查询范围;同时也可以提前提取一些确定的结果集轨迹对,提升算法的效率。同时将查询空间网格化,在网格上进行范围查询,可以有效提高查询效率。对于范围查询到的轨迹点进行一系列操作,就可以得到满足用户要求的结果[11]。本文贡献如下:
(1) 在研究轨迹空间相似性的基础上,增加了对于文本相似性的考虑。
(2) 通过空间、文本两方面因素对于最终轨迹相似性贡献权重的调整,得出空间和文本相似性的阈值范围,便于进行剪枝。
(3) 对于空间进行网格化处理,在空间网格上根据满足要求的范围进行范围查找,提高效率。
1 相关工作
文献[1]研究了道路网络中行驶车辆的轨迹相似性查询(TS-Join)。该文为了实现在大量的轨迹上高效的轨迹相似性查询,提出了空间修剪技术并考虑并行处理能力。文献[3]解决了用于大量移动轨迹的有效相似性查询问题。与以前方法不同的是,该文认为在许多基于位置的服务应用中,轨迹已按原样在其原生空间中编入了索引。在这个前提下,在变换的空间中使用专用索引,便于处理常见的时间和空间方面轨迹相似性查询。同时该文介绍一种从经典的弗雷歇距离中改编新颖的距离,可以自然地延伸来支持利用上下限对于在原生空间中的移动对象数据库进行索引。文献[2]研究空间关键词范围搜索问题,这对于理解大量数据轨迹至关重要。为了进行有效的条件搜索,提出了一个被称为IOC-Tree的基于倒排树和八叉树技术的空间网格索引结构对空间、时间和文本进行有效的剪枝。
本文在空间距离方面使用DTW进行计算,在文本方面用Jaccard系数进行计算[16],运用范围查询相关技术并通过一系列定理来进行轨迹相似性计算,将空间网格化划分进而进行范围查询剪枝,提高算法的效率。
2 问题的形式化定义
2.1 基本定义
空间轨迹上任意轨迹点对象均包含地理位置和文本关键字集合,对于任意一个轨迹点对象pi都是包含地理位置和文本关键字集合的轨迹点对象。每一个轨迹点对象的存储形式pi(x,y,K,Rid),空间文本信息记为K,K={a1,a2,…,an},ai是文本关键字[10]。x、y分别为轨迹点对象的经纬度,Rid为轨迹点对象所在的轨迹编号。对于轨迹集合中的任意一条轨迹都由n个轨迹点对象组成,记为R(p1,p2,…,pn)[13]。
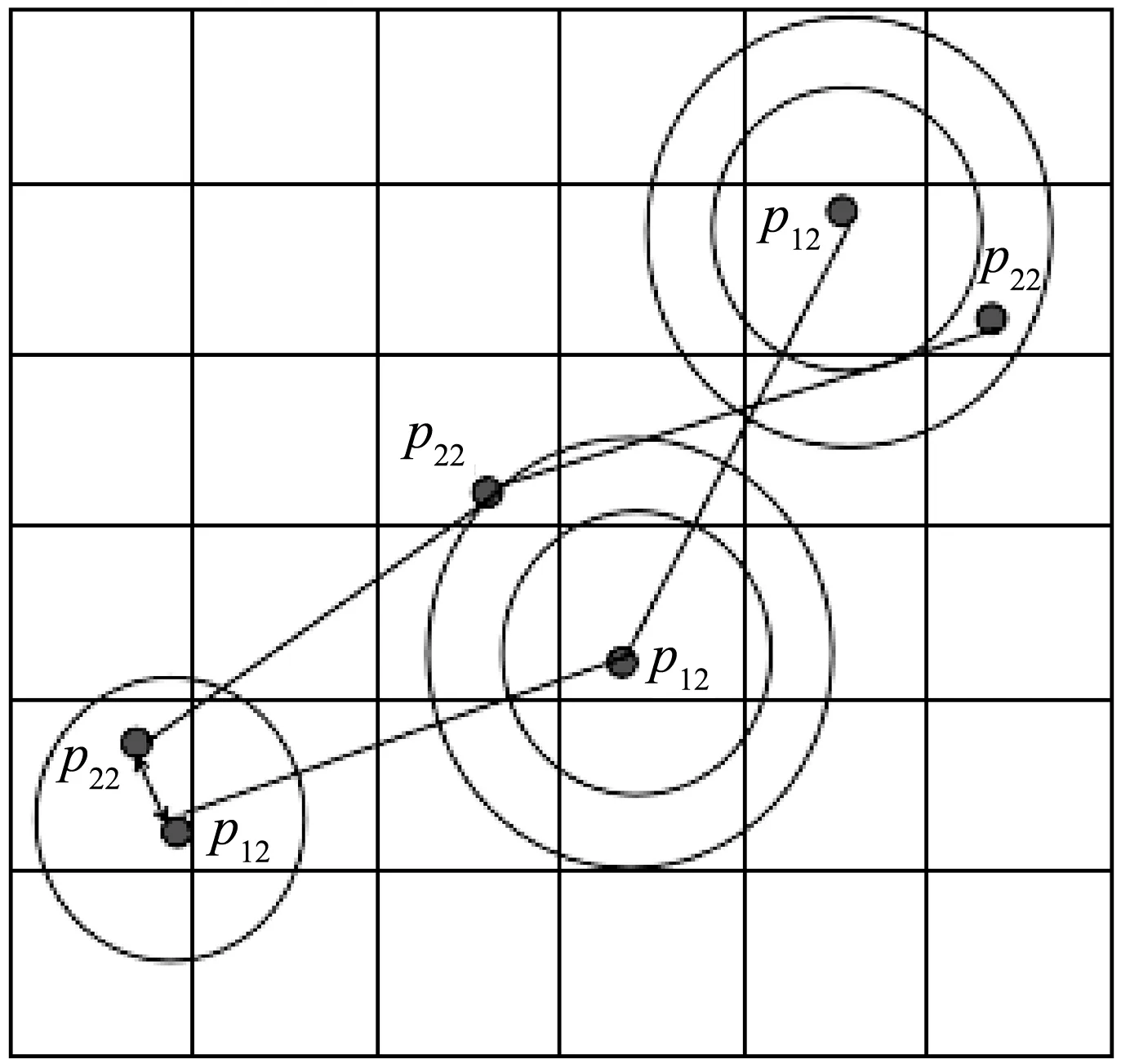
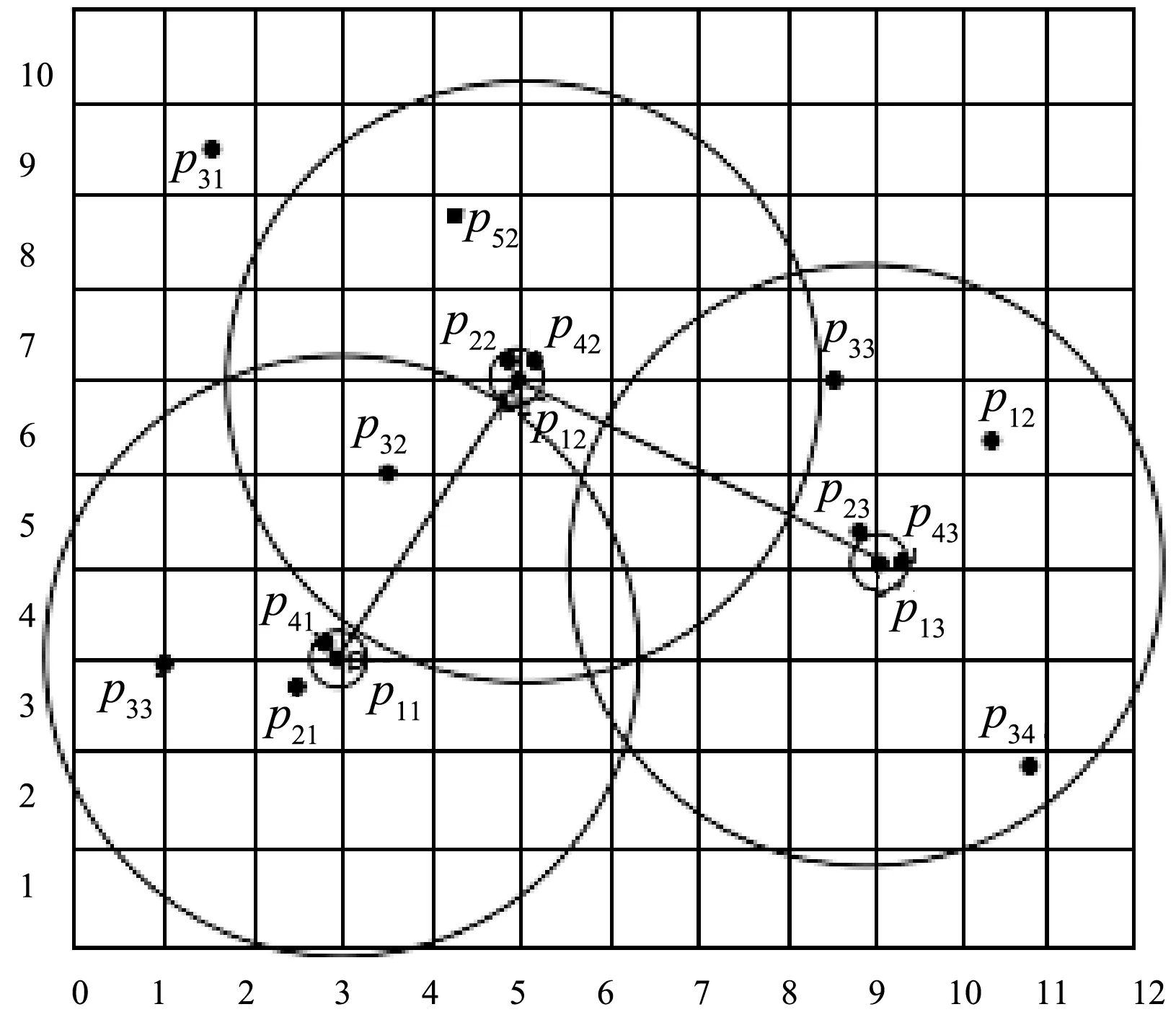
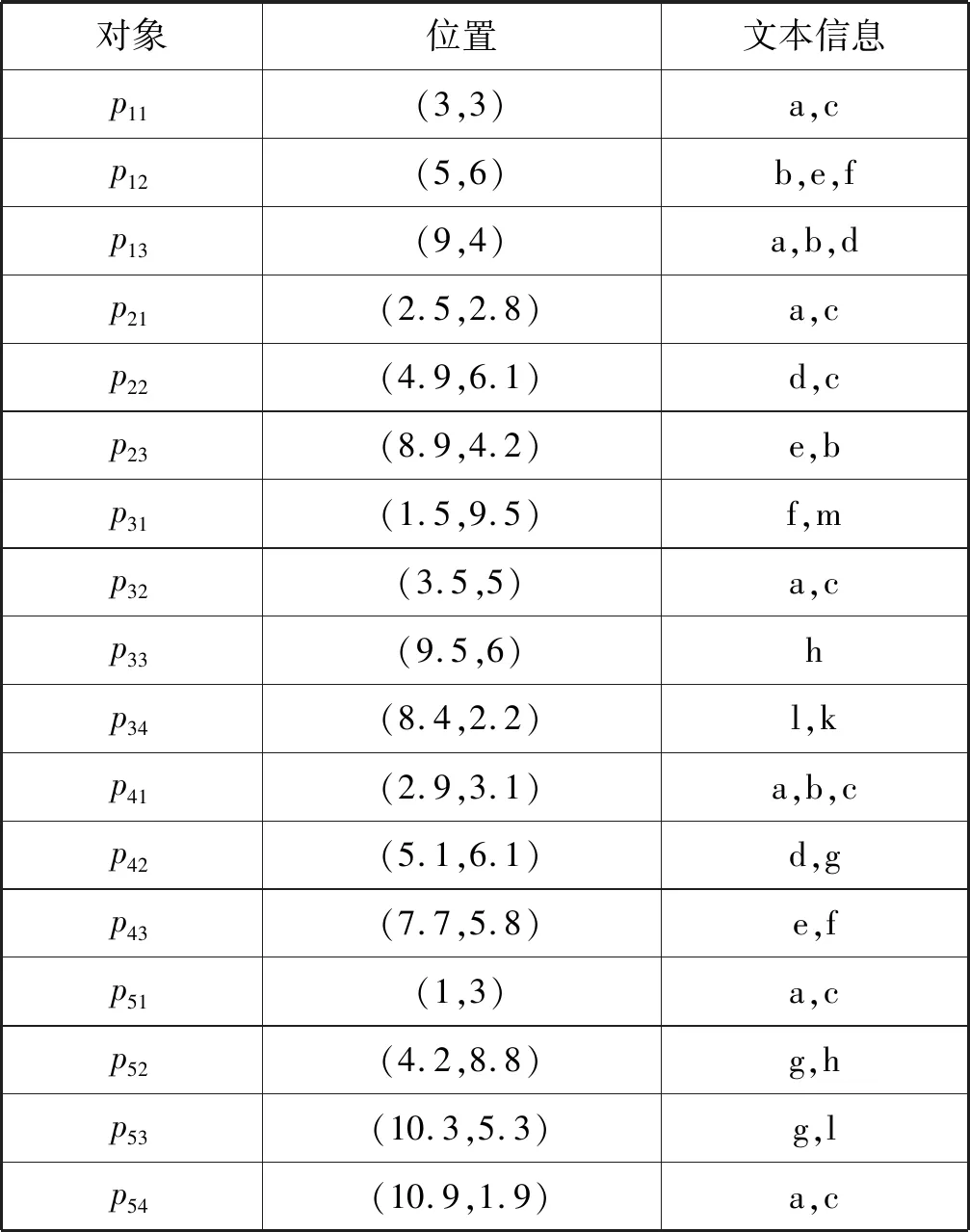
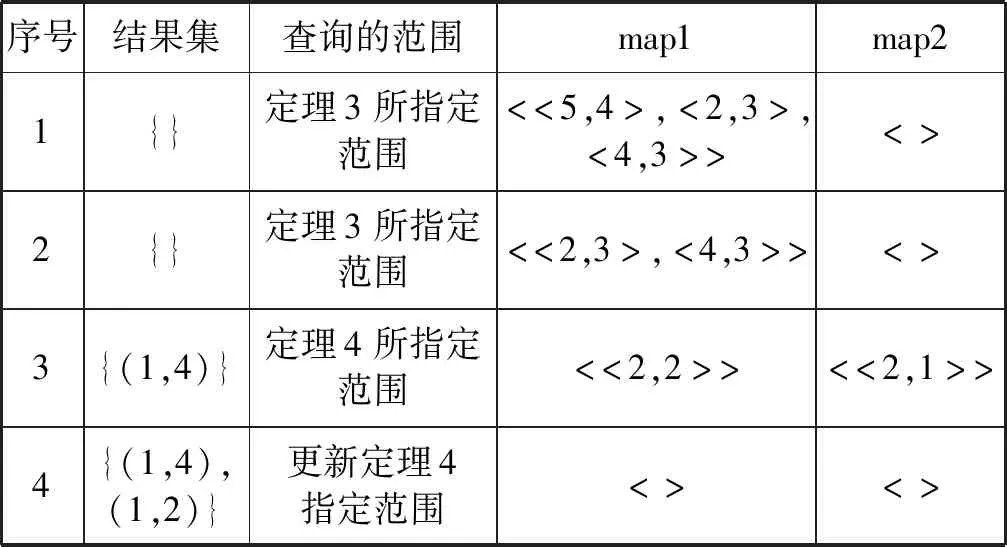
定义1(空间文本轨迹) 空间文本轨迹R由点p1,p2,…,pi,…,pn组成,其中每个点pi=(xi,yi,tmi),表示对象在时刻tmi位于(xi,yi)位置,其中tm1 如图1所示,轨迹t1由三个轨迹点p11、p12、p13组成,因此轨迹t1的长度是3;在轨迹t1的p11轨迹点那一时刻,轨迹t2、t3分别位于p21、p31轨迹点处;对于轨迹t1的关键字集合就是组成轨迹t1的各个轨迹点所带的关键字集合,即{coffee,cinema,shop,library,swim}。 给定一条轨迹t,轨迹集合中任意一条轨迹t′与轨迹t的空间相似度、文本相似度和空间文本相似度的定义如下: 定义2(轨迹空间相似度) 任意两个轨迹在空间中的相似程度记为SIMs(t,t′)用两条轨迹间的空间距离表示。设dmax表示空间中任意两条轨迹之间的最远距离,则空间中任意两条轨迹t和t′的相似度定义为: (1) 由式(1)知两个轨迹间距离越近,轨迹的空间相似性就越大。由于DTW算法不要求轨迹等长也可完成轨迹点的动态匹配,因此本文采用DTW计算任意两条轨迹之间的空间距离。 定义3(轨迹文本相似度) 任意两个轨迹的文本相似性,记为SIMT(t,t′)。即文本集合的相似度,用Jaccard系数计算获得。 (2) 由式(2)可知,两个轨迹之间文本集的交集的元素个数越多,SIMT(t,t′)的值越大,文本相似性就越大。 定义4(轨迹空间文本相似度) 结合定义2和定义3,任意两个轨迹之间的相似性定义为: SIM(t,t′)=αSIMS(t,t′)+(1-α)SIMT(t,t′) (3) 式中:α(α∈[0,1])是一个可调节参数,用以调节计算空间文本相似性时空间因素与文本因素之间的相对重要程度。SIM(t,t′)的值越大,两条轨迹之间的空间文本相似度就越大。 表2给出图1中轨迹t1与轨迹t2的空间距离。 表2 轨迹t1和t2之间的DTW距离 由表2可知轨迹t1和轨迹t2之间的距离为1.33,根据同样的方法计算其他轨迹对之间的距离,可得dmax=5.66,根据定义1可得轨迹t1和t2的空间相似度为0.77;根据表1可知t1与t2的文本并集个数为7,文本交集个数为1,根据定义3可得t1与t2的轨迹文本相似度为0.143。若给定的α值为0.5,根据定义4可得最终t1与t2的空间文本相似度为0.46。 本文的问题描述如下:给定一个轨迹的集合P和一个阈值ψ,轨迹相似性查询是从一个轨迹集合中找出任意两条轨迹的相似性大于给定阈值ψ的轨迹对集合。 由于轨迹数量十分庞大,为提高查询效率,需要先将一部分完全不可能存在在结果集中的轨迹剪枝掉。通过观察式(3)发现,在轨迹相似度阈值确定的情况下,如果两条轨迹文本相似度(空间相似度)取最大值(即1),则空间相似度(文本相似度)将取最小值。对于任意一条轨迹t,如果其他轨迹到该轨迹的空间相似性(文本相似性)小于这个最小值,则这些轨迹一定不在查询轨迹t的相似性结果集中。因此,相似度下限如定理1。 定理1(相似度下限) 给定轨迹空间文本相似度ψ和参数α,对于任意一条轨迹t的空间相似度下限和文本相似度下限分别为: (1) 空间相似度下限LB_SS:对于轨迹集合中另外任意一条轨迹t′,若两者的文本相似度取最大值1,则根据式(4)可以计算出空间相似度下限,表示为: LB_SS=(φ+α-1)/α (4) 由于空间相似度与空间距离成反比。根据空间相似度下限,可以得到空间两条轨迹之间最大距离下限,即SD_LBmax。根据定义2可以计算出空间两条轨迹之间最大距离的下限: SD_LBmax=dmax[(1-φ)/α] (5) (2) 文本相似度下限LB_ST:对于轨迹集合中另外任意一条轨迹t′,若两者的空间相似度取最大值1,则根据式(3)可得文本相似度下限,如下: LB_ST=(φ-α)/(1-α) (6) 根据文本相似度下限,设MINks是轨迹上包含的最小文本数,可得两条轨迹之间的最小相同文本数Wmin: Wmin=MINks×LB_TT (7) 由于在轨迹集合中任意两条轨迹的并集集合数都大于MINks,因此MINks是两条轨迹并集集合数的下限,根据定义3,在文本相似度取最小值时,由此下限乘以文本相似度下限,得到相同文本数是最小值。 若其他任何轨迹t′与t的空间相似度小于LB_SS,则轨迹t′不会存在于轨迹t的相似轨迹集合中。 证明:对于空间相似度下限来讲,已知轨迹集合R,用户要求的空间文本相似度为ψ,给定一条轨迹t,其他任何轨迹t′与t的文本相似度取最大值1;对于R中任意轨迹对象Ri,SIMT(Ri,t)≤1,SIMS(Ri,t) 同理可证,对于给定的一条轨迹t,其他任何轨迹t′与t文本相似性小于LB_TT,则轨迹t′不会存在于轨迹t的相似轨迹集合中,被剪枝。 同样,对于空间相似度下限和文本相似度下限来说,也可以用另一种方式说明,即空间最大距离下限和最小相同文本数,因此同理可以证明,当轨迹t′与t的相同文本数小于最小相同文本数或者轨迹t′与t的空间距离大于空间轨迹最大距离的下限时,就将轨迹t′剪枝掉。 证毕。 与之相反,在轨迹相似度阈值确定的情况下,式(4)中如果两条轨迹文本相似度取最小值(即0),则空间相似度将取最大值。对于任意一条轨迹t,如果其他轨迹t′到t的空间相似性大于这个最大值,则t′一定在t的相似性结果中。由此,空间相似度上限形式化如定理2。 定理2(空间相似度上限) 给定轨迹相似度阈值ψ,一条轨迹t,如果其他任何轨迹t′与t的空间相似度大于UB_SS,则轨迹t′一定存在于轨迹t的相似轨迹集合中。表示为: UB_SS=φ/α (8) 由于空间相似度与空间距离成反比,则根据定义2,可得空间轨迹最小距离的上限为: SD_UBmin=dmax(1-φ/α) (9) 证明:对于空间相似度上限而言,已知轨迹集合R,用户要求的空间文本相似度为ψ,给定一条轨迹t,其他任何轨迹t′与t的文本相似度取最大值0;对于用户给定轨迹集合R中的任意轨迹对象Ri,都有SIMT(Ri,t)≥0;因为UB_SS是在SIMT(Ri,t)=0情况下计算出的结果,所以如果要满足用户的相似度φ,不管Ri和t之间的文本相似度值取何值,若SIMS(Ri,t)≥UB_SS,则SIM(Ri,t)=αSIMS(Ri,t)+(1-α)SIMT(Ri,t)≥φ,一定满足用户要求。 证毕。 在定理1和定理2中,分别获得了任意两条轨迹的空间距离的最大距离下限SD_LBmax和最小距离上限SD_UBmin。根据最小距离上限SD_UBmin,得到紧凑的最小距离上限。轨迹t′中若有任意点的位置在最大距离下限之外,则轨迹t′被剪枝;轨迹t′上的所有点都在紧凑的最小距离上限内,则轨迹t′一定是查询结果之一;否则我们通过逐步上调SD_UBmin,进而调整紧凑的最小距离上限,对轨迹t′做进一步的验证。同样算法根据最大距离下限SD_LBmax,也可得到紧凑的最大距离上限。通过这个距离,可对算法进行一些改变,得到另外一种解决问题的方式,算法部分会给出具体介绍。 根据最大距离下限做范围查询,可以对轨迹进行一些剪枝。 定理3给定轨迹t和任意一条轨迹t′,若以t中的每一个位置点为圆心,以SD_LBmax为半径做范围查询,若轨迹t′中存在任意一个点在范围查询之外,则轨迹t′被剪枝。 证明:假设给定一条查询轨迹t,有n个轨迹点;轨迹集合中的任意一条轨迹t′,有m个轨迹点;此时定理3所指定的范围的半径是SD_LBmax,当把两个轨迹之间的最大距离上限用在单点上时,对于每一个单点来说,如果在这个范围之外,根据DTW计算两条轨迹之间的规律,经过层层迭代,我们可以知道最终距离总是会加上一个SD_LBmax。因此,只要有一个轨迹点在定理3所指定的范围之外,那么轨迹t′和轨迹t的距离就会大于SD_LBmax。在定理1中我们已经证明了如果两条轨迹之间的距离大于SD_LBmax,那么就可以直接被剪枝。 因此只要有一个轨迹点在定理3所指定的范围之外,一定不是备选轨迹,将其剪枝掉。 证毕。 (1) 紧凑的最小距离上限:可以将最小距离下限SD_UBmin通过式(10)变得更紧凑些。 r1=SD_UBmin/n′ (10) 式中:n′是轨迹t和轨迹t′中轨迹长度较大的轨迹长度。 定理4给定轨迹t和任意一条轨迹t′,若以t中的每一个位置点为圆心,以r1为半径做范围查询,若轨迹t′中所有点在范围查询之内,则轨迹t′一定在轨迹t的结果集合中。 证明:假设给定一条查询轨迹t,有n个轨迹点;对于轨迹集合中的任意一条轨迹t′,假设有m个轨迹点;当n=m时,定理4所指定的范围大小为SD_UBmin/n,若轨迹t′上的所有轨迹点都在定理4指定的范围之内,根据DTW计算两条轨迹距离的规律,对于最终两条轨迹之间起决定作用的各个对应轨迹点之间的距离,由于轨迹t′的所有轨迹点都在轨迹t的定理4所指定的范围中,所以各个对应轨迹点之间的距离都是小于SD_UBmin/n,当有一个对应的轨迹点之间的距离小于SD_UBmin/n,再往下推算两条轨迹之间距离时,就可以知道在这个对应下一层是由一个小于SD_UBmin/n的数加上下一层的对应轨迹点之间的距离,同样因为下一层对应轨迹点依然是小于SD_UBmin/n,因此经过一层层的推算,可以得到最终轨迹t′到轨迹t的距离小于SD_UBmin/n;当m>n时,此时定理4指定的范围大小是SD_UBmin/m,同样根据DTW计算两条轨迹距离的规律,两条轨迹点相同的部分参照两条轨迹点相同的情况给出,即两条轨迹点相同的部分计算出一个最终值小于SD_UBmin×n/m,考虑较长轨迹的剩余部分,容易知道最终两条轨迹之间的距离小于SD_UBmin;当m 因此轨迹上轨迹点完全在定理4指定范围之内的轨迹一定属于结果集。 证毕。 (2) 紧凑的最大距离下限:根据最小距离下限SD_LBmax,可以通过下式变得更紧凑些。 r2=SD_LBmax/n′ (11) 式中:n′是轨迹t和轨迹t′中轨迹长度较大的轨迹长度数。 定理5给定轨迹t和任意一条轨迹t′,若以t中的每一个位置点为圆心,以r2为半径做范围查询,若轨迹t′中所有点在范围查询之内,则轨迹t′一定是轨迹t的备选结果集合。 证明:参照紧凑的最小距离上限证明方法,同时根据DTW计算规律可以得到完全在紧凑的最大距离下限所给定的范围之内的,一定是轨迹t的候选结果轨迹。 证毕。 算法分为三个步骤:第一步,剪枝。给定轨迹t,先在轨迹t上每一个位置点上执行定理3所指定的范围查询。如果对于轨迹集合中任意一条轨迹t′,有任意轨迹点位于范围查询之外,则轨迹t′被剪枝并形成初步相似轨迹候选集candk。candk中任意的轨迹t′,如果与轨迹t的相同文本数小于Wmin,则从candk中去除t′。如此,完全在最大范围下限范围查询内且满足最小相同文本数要求的轨迹组成了相似轨迹候选集cand。第二步,确定结果集。对于在轨迹t上每一个位置点上执行定理4指定的范围查询,如果对于cand中的任意轨迹t′的所有位置点都在此范围内,则从cand中去掉t′并返回结果(t,t′)。第三步,候选结果集求精。对于cand中剩余轨迹,调整定理4所指定的范围,重新进行范围查询,如果对于轨迹t′所有轨迹点在调整范围过程中被访问到,则从cand中去掉t′并返回(t,t′);重复上述操作直至调整范围的半径大于SD_UBmin。若cand中依然存在没有被完全访问到的轨迹,取出该轨迹的具体信息,验证其是否为结果。 下面对于候选结构求精步骤进行详细介绍: r′=(SD_UBmin-sd)/(n-1) (12) 再次进行定理4所指定的范围查询,对于范围查询中访问到的轨迹点,判断是否为t′上的轨迹点,如果t′上的轨迹点被访问完全,那么返回(t,t′);否则计算访问到的各个点与在查询轨迹t上对应的轨迹点之间的距离,在这些距离中取最大值更新sd,进而更新r′,重复进行上述步骤,直至r′大于或者等于SD_UBmin。 如果在上述停止条件出现之后,cand中依然存在轨迹点,那么取出轨迹点所在轨迹的具体信息,计算其与查询轨迹t的空间文本相似度判断是否符合用户要求,如果符合就纳入结果集,否则就剪枝掉。接下来用图2来解释我们的验证算法。 图2 验证例图 对于图2来说,此时查询轨迹是由p11、p12、p13组成的轨迹1,验证轨迹是由p21、p22、p23所组成的轨迹2,图中较小的圈就是我们定理4所指定的范围;由于p21在定理4所指定的范围中,所以我们计算p21到p11之间的距离,根据这个距离我们就可以更新查询轨迹上p12、p13点所对应的范围,即如图2所示外面较大的圈。紧接着判断是否在新一次的范围查询中查询到所有验证轨迹2的轨迹点,可以得到轨迹对(1,2)在最终的结果集中。 本文通过对于空间(文本)相似度取最大或最小值,从而得到文本(空间)的最小或最大值,在计算的过程中,对于φ和α的取值,会有大小的冲突。因此在算法中,对于最小距离上限的计算,将本文相似性从0的取值更新至当前备选轨迹集合中文本相似度的最小值,证明可参考定理2中的证明过程,结论依然成立。那么此时SD_UBmin的计算公式如下: (13) 具体算法如下: Input:用户要求的相似性φ,参数值α,轨迹集合R Output:满足用户相似性要求的轨迹集集合A 1. for轨迹集合R中的每一条轨迹Ri 2. 计算SD_LBmax=dmax[(1-φ)/α]; 3. for在定理3所指定的范围的每一个轨迹点对象Xi 4. 将 5. for在map1中的每一个轨迹点对象Xi 6. if(map1中t′的轨迹点个数<轨迹t′的个数) 7. 剪枝掉轨迹t′,形成candk; 8. 计算LB_ST=(φ-α)/(1-α)Wmin=W*LB_ST 9. for candk中每一个轨迹点对象Xi 10. if(Xi所在轨迹t′与Ri的相同文本数 11. 剪枝掉t′,形成cand; 12. for cand中每一个轨迹点对象Xi 13. if(Xi所在轨迹t′的轨迹点数==查询轨迹t轨迹点数) 14. 计算cand中轨迹的文本最小值记为SIMTmin; 15. 计算SD_UBmin=dTminmax; 16. 计算r1=SD_UBmin/n′; 17. if(Xi在定理4所指定范围内) 18. 将 19. if(map2中Xi对应轨迹编号t′的轨迹点数==此时map1中t′的轨迹点个数) 20. 将(t,t′)加入结果集A中; 21. else 22. 进一步验证map1,map2中剩余轨迹否为结果集; 23. else if(Xi所在轨迹的轨迹点对象个数>Ri的轨迹点对象个数) 24. 更新SD_UBmin,r1,重复执行11-21行; 25. ReturnA; 对于用户给定轨迹集合中的每一条轨迹Ri,首先计算SD_LBmax,(1-2行)。对于查询轨迹t构造定理3所指定的范围,进行范围查询,对于访问到的轨迹点Xi,将 对于cand中的每一个轨迹点Xi,判断Xi所在的轨迹t′的轨迹点个数是否等于查询轨迹的轨迹点个数。如果相等,计算cand中轨迹的文本相似性的最小值SIMTmin和SD_UBmin,之后计算紧凑的最小距离上限r1;对于查询轨迹Ri构造定理4所指定的范围,进行范围查询(13-16行)。判断Xi轨迹点是否被访问到。如果被访问到了,将 在算法中可以将定理3指定的范围改变为定理5指定的范围,同样执行范围查询。但是在进行最小文本数剪枝之前,需要增加一个验证算法,验证部分在定理5指定范围内的轨迹是否为备选结果集。该验证算法与上述验证算法相同。 因此,还有另外一种算法去解决这一问题,即把上述算法的2-4行改变为: 2. 计算SD_LBmax=dmax[(1-φ)/α] r2=SD_LBmax/n′; 3. for在定理5所指定的范围的每一个轨迹点对象Xi 4. if(Xi所在轨迹的轨迹点对象个数==Ri的轨迹点对象个数) 5. 将 6. if(map1中Xi对应轨迹编号t′的轨迹点数=0) 7. 将轨迹t′从map1中剪枝掉; 8. else 9. 验证该轨迹是否备选轨迹; 对于算法部分,本文提出了两种解决问题的算法。由于不同的数据集会有不同的数据分布,这两种算法也会有不同的运行效率。同时对于相同的数据集可能也有运行时间上面的不同。 给定一条查询轨迹t,有n个轨迹点。 2. 取map2中的轨迹对应的任一轨迹点对象Yi 5. 根据d,对栈nbs进行从大到小排序,取栈顶d记为sd; 8. for(更新范围内的每个轨迹点) 9. 重复执行3-7行; 10. 记录栈内轨迹出现的次数N,和栈顶轨迹出现的次数N′; 11. if(栈顶对应的轨迹的轨迹点个数==N′) 12. 将栈顶对应的轨迹和查询轨迹组成轨迹对加入结果集中 13. else 14. 从磁盘中取出相应的轨迹信息,进行计算验证 15. if(nbs中其他轨迹的轨迹点==N) 16. 将该轨迹和查询轨迹组成轨迹对加入结果集中; 18. else 19. 重复执行4-14行。 给定一个例子来详细介绍算法的流程。如图3所示,整个的矩形空间是本文算法的查询范围,其中每个点都是轨迹点。 图3 轨迹相似性示例 由图3可知,在整个进行空间中,有5条轨迹,轨迹的详细信息如表3所示。 表3 图3中轨迹信息 表4为上述运行过程的运行示例表。通过对于每次访问区域的更新,得到备选轨迹集和结果集的更新,最终得到满足用户要求的轨迹对结果集合。 表4 运行示例表 第一步,给定用户要求的相似性φ=0.9,α=0.5;给定一条查询轨迹t1(p11,p12,p13);计算出SD_LBmax=3.39;进而根据查询轨迹的轨迹点得到定理3所指定的区域,即图3中大圈所含区域。根据访问空间中轨迹点的位置信息,对每一个轨迹点判断是否在定理3所指定的范围内,经过判断,此时map1中有<<5,4>,<2,3>,<4,3>>,构成初步的备选轨迹集合candk。 第二步,计算出Wmin=5,candk中的轨迹5与轨迹1的相同文本数为2,小于5,剪枝掉轨迹5。此时map1中有<<2,3>,<4,3>>,构成最终的轨迹备选集合。进而得到目前轨迹集合中最小的文本相似度为0.83。 第三步,计算出SD_UBmin=0.54,r1=0.18,进而得到定理4所指定的范围。对于cand中的每一个轨迹点,判断该轨迹点是否在定理4所指定的范围内。以p21为例,根据p21轨迹点的位置,易知p21不在定理4所在指定的范围之内,不可将该点加入map2,所以map2中存入<<4,1>>。重复上述的判断,可得最终map2中为<<4,3>,<2,1>>,map1中为<<2,2>>。根据map2中的轨迹信息可知,轨迹4在map2中的轨迹点数等于自身的轨迹点个数,即轨迹4完全在定理4所指定的范围之内,因此将(1,4)纳入结果集A。 因此最终满足用户要求的结果集中有{(1,4),(1,2)}。 随着移动互联网的高速发展和移动定位设备的广泛普及,基于位置的地理信息服务逐渐渗透进人们生活的方方面面。随之而来的对于基数庞大的轨迹数据研究成为热点。本文研究轨迹相似性,在一般的空间相似性研究的基础上,加入了对于轨迹文本相似性的考虑,使得对于轨迹相似性的研究更为全面,未来这一算法可以推广到旅游路线推荐的应用开发中。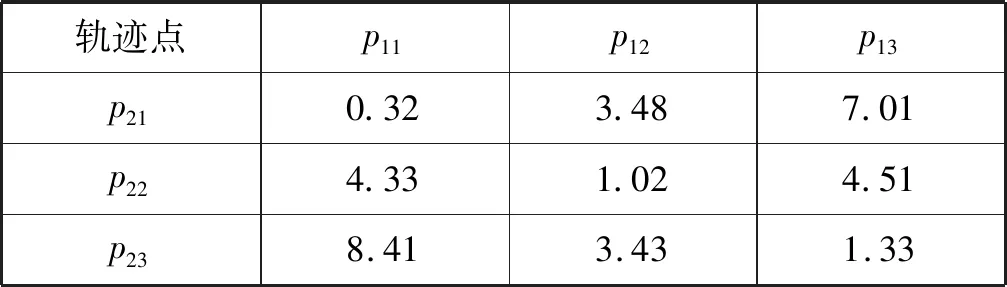
2.2 相关定理
3 算法设计
3.1 距离介绍
3.2 基本步骤
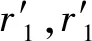
3.3 具体流程



4 运行示例
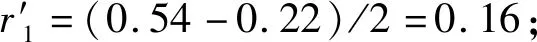
5 结 语
