一种基于全变分滤波的单幅图像快速去雾算法

唐 斌 马思根 陈清容 龙 文

1(贵州财经大学信息学院 贵州 贵阳 550025)2(贵州财经大学贵州省经济系统仿真重点实验室 贵州 贵阳 550025)

0 引 言

在有雾的低照度环境下，摄像机、数码相机等图像传感器所采集的视频或图像通常能见度较低，图像纹理可辨识度不高。在进行机器识别或目标跟踪之前需要对有雾图像做清晰化预处理。

有雾图像清晰化处理的方法层出不穷。根据其使用技术的特征，可将去雾算法分为两大类。第一类是以增加对比度为目的的增强算法。使用直方图均衡的方法是通过拉伸方式改变像素值的分布概率达到增强对比度的目的，但可能会丢失图像的部分细节[1]。Retinex理论[2]认为有雾图像是由环境光照射分量和物体表面反射光分量组成，那么可以使用同态滤波减弱环境光照射分量从而提高反射光分量，最终增加对比度，但是该类方法容易出现偏色问题。第二类是基于大气散射模型的还原算法，该类方法的关键在于估算透射率和大气环境光。He等[3]发现暗原色先验理论并利用此理论估算透射率，该方法简单易行，去雾效果较好，但存在Halo效应，处理速度较慢。Zhu等[4]发现颜色衰减先验理论，构建了场景深度与亮度、饱和度之间的线性模型，根据此模型可以计算透射率。该方法同样简单可行，去雾后的图像清晰，但线性模型中的系数容易受训练数据集影响。Kim等[5]以图像均方误差和信息丢失量构建了一个反映对比度的成本函数，通过最大化成本函数的方法获取透射率。该方法不仅适合非天空区域，也适用于天空区域，但存在偏色现象。由于深度学习在图像识别领域的卓越表现，基于卷积神经网络去雾的算法逐渐出现。Cai等[6]构建端到端的卷积神经网络DehazeNet，通过深度学习提取有雾图像特征而估算透射率，但深度学习需要大量的数据集训练。

本文采用第二类方法去雾，根据每个像素点的最小颜色值和全局大气环境光值估算粗糙大气透射图。粗糙大气透射图除了包含有景深边缘外，还包含部分纹理信息，因此再使用全变分滤波平滑粗糙大气透射图的纹理信息和保留景深边缘，全变分滤波迭代次数与滤波效果成正比关系，但会增加去雾时间。为降低计算复杂度，在全变分滤波前，对粗糙透射图下采样再进行全变分滤波，最后获取精细大气透射图。

1 大气散射模型

根据大气散射模型理论[7]，物体表面光在雾天环境中传播时会因为颗粒的散射作用而出现衰减，因此图像传感器设备采集的图像可用如下模型描述：

I(x)=J(x)e-βd(x)+A(1-e-βd(x))

(1)

式中：J(x)表示无衰减的无雾图像；A表示大气环境光；e-βd(x)为衰减系数，也称为大气透射率t(x)；β为大气散射系数；d(x)为景深。受颗粒的散射作用影响，无雾图像和大气环境光分别衰减为J(x)t(x)和A(1-t(x))(大气耗散函数)，图像传感器采集的有雾图像I(x)则由这两个衰减项之和组成。

式(1)中，已知条件为有雾图像，在缺乏其他约束条件的情况下，无雾图像的值存在着多种可能。为恢复无雾图像，需要从有雾图像中提取大气环境光A和大气透射率t(x)。

2 粗糙大气透射率

2.1 大气环境光

通常采用有雾图像比较明亮的像素值估算大气环境光。He等[3]对有雾图像的RGB像素值进行降序排序，然后检索出前0.1%值所对应的像素点坐标，这些坐标对应像素点的RGB三个平均值就是三个颜色通道的大气环境光值。大量的实验结果表明：使用这种大气环境光复原后的图像亮度偏暗，颜色偏蓝。Kim等[5]认为大气环境光与白色(RGB三个颜色值都为255)最接近，但有雾图像中存在的白色发光物体会干扰大气环境光值的估算。为了排除这种干扰，可以采用四叉树方法搜索最接近白色的像素点。具体方法是：将有雾图像切割成四个图像块，选取均方差最小的图像块继续切割成四部分，直至切割图像块尺寸小于阈值才停止，然后在均方差最小的图像块中搜索出最接近白色的像素点，该像素点的RGB值就是大气环境光值。大量的实验结果表明：使用这种大气环境光复原后的图像亮，颜色偏黄。

在估算大气环境光前，首先对有雾图像进行伽玛矫正，然后分别使用He等[3]和Kim等[5]的方法估算出两种大气环境光值，最后使用线性加权方法获取最终大气环境光。计算方法如下：

A=αAHE+(1-α)AKIM

(2)

经过多次试验观测，α的经验值设置为0.6。

2.2 相关函数

大气耗散函数A(1-t(x))中包含有大气透射率t(x)，因此本文使用该函数估算大气透射率。假设V(x)=A(1-t(x))，那么大气透射率的估算公式如下:

(3)

大气耗散函数V(x)如果直接使用有雾图像每个像素点的最小颜色值W(x)，那么结合大气环境光A，估算出的粗糙大气投射率如下：

(4)

式中:粗糙大气透射率最小值设置为0.2；系数ω设置为0.95。式(4)估算的值之所以称为粗糙大气透射率，是因为W(x)不仅包括了较多跃变的景深边缘信息，还具有较多平滑的图像纹理信息。虽然景深边缘信息可以用来估算透射率，但图像纹理信息对透射率的估算具有干扰作用。

3 精细大气透射率

3.1 全变分滤波

Rudin等[8]提出的全变分模型具有平滑细节和保留边缘特点，广泛应用于图像去雾领域[9-13]。基于全变分的图像降噪可以用极小化能量泛函如下描述：

(5)

式中：第一项是基于l1范数的全变分正则项，其作用是保留扩散系数小的边缘，平滑扩散系数大的平坦区；第二项是基于降噪图像u与噪声图像i之间差值平方的拟合项，其作用是确保降噪图像u与原始图像具有较高的相似度，λ为正则项和拟合项的平衡系数。

根据极值条件和变分法，极小化能量泛函需要对欧拉-拉格朗日方程求解。该方程可以使用梯度下降法、迭代法或Bregman法求解，但这三种求解方法都不够简练。Gong等[14]设计了一种新的全变分滤波器，使用滤波的方法最小化正则项，从而获取降噪图像u。全变分滤波器的输入为BT、WT、WC和BC等四幅无交集图像。这四幅图像数据分别取自于噪声图像坐标为(2n,2n)、(2n,2n+1)、(2n+1,2n)、(2n+1,2n+1)所对应点的像素值。具体对应关系如图1所示,图中黑色三角形、白色三角形、白色圆形和黑色圆形分别表示BT、WT、WC和BC的像素。

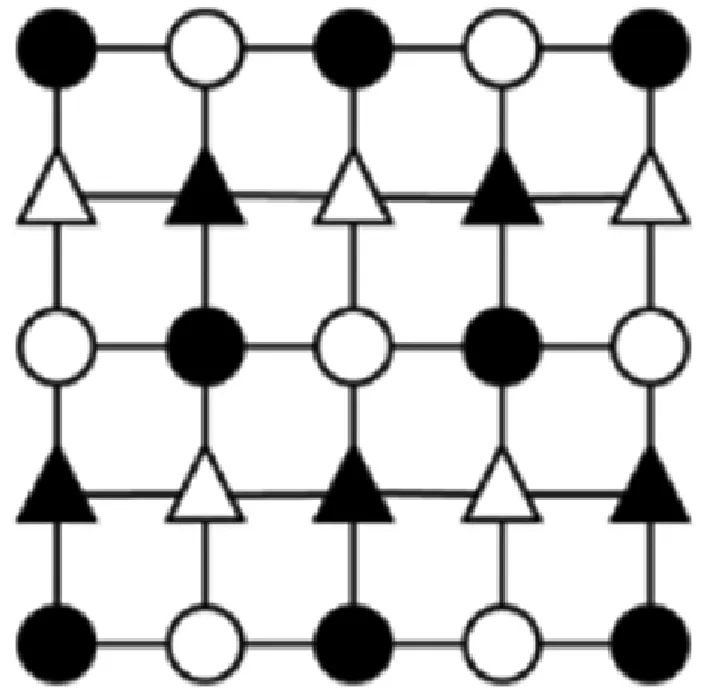
图1 BT 、WT 、WC、BC坐标图

将噪声图像切割成BT、WT、WC和BC四幅子图像后，对每幅子图像单独进行全变分滤波。全变分滤波工作原理为：以过中心像素点的对称轴将尺寸为3×3的全窗口切割成两部分，计算半窗口内除中心像素点外其他5个像素的平均值，然后计算该平均值与中心像素点的差值。由于3×3的全窗口存在4条对称轴，故对应的差值存在8个。选取绝对值最小的差值更新中心像素点。以图2为例，全变分滤波细节如下：

(1) 以过中心像素点P0的对称轴为分界线，将图2切割成8个不同的半窗口。

(2) 计算下列表达式计算8个不同的差值di。

d0=(P1+P2+P3+P4+P5)/5-P0

(6)

d1=(P2+P3+P5+P7+P8)/5-P0

(7)

d2=(P4+P5+P6+P7+P8)/5-P0

(8)

d3=(P1+P2+P4+P6+P7)/5-P0

(9)

d4=(P1+P2+P3+P5+P8)/5-P0

(10)

d5=(P1+P4+P6+P7+P8)/5-P0

(11)

d6=(P1+P2+P3+P4+P6)/5-P0

(12)

d7=(P3+P5+P6+P7+P8)/5-P0

(13)

(3) 选择最小值di采用下列公式更新中心像素P0的值。

P0=P0+min{|di|,i=0,1,2,3,4,5,6,7}

(14)

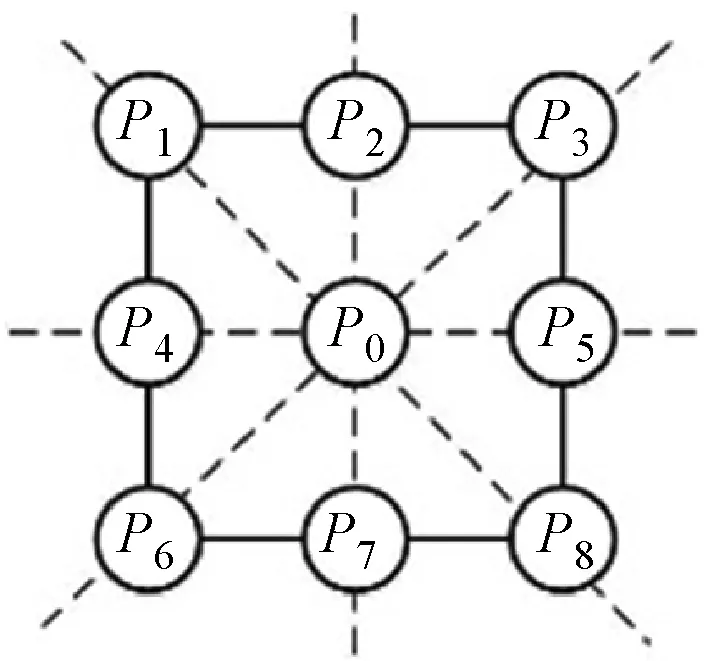
图2 WC半窗口切割方法

3.2 计算过程

为了获取精细大气透射率，还需要滤除W(x)中的纹理细节，同时保留跃变景深边缘信息[15]。全变分滤波对全变分值大的跃变景深边缘具有保持作用，对全变分值小的纹理信息具有平滑作用，因此使用全变分滤波获取精确的大气耗散值。其计算过程如下：

(15)

WTV(x)=TVfilter(Wdown(x),iteration)

(16)

WUP(x)=imresize(WTV(x),scale,′bicubic′)

(17)

全变分滤波需要通过多次迭代才可以获取较好的保边去细节效果，但增加迭代次数(itertation)会增加滤波时间从而牺牲实时性。为减少计算时间，本文没有直接对W(x)进行全变分滤波，而是采用式(15)对W(x)进行下采样，然后使用式(16)进行全变分滤波，最后使用式(17)进行上采样恢复精确大气耗散值，将该值代入式(3)即可获取精细透射率。由于图像缩放同样具有均值滤波功能，因此缩放比例scale的设置非常关键，常用的缩放算法包括最临近值法、双线插值法和双三次插值法(bicubic)，其中双三次插值算法缩放后的图像比较光滑，因此本文选择双三次插值算法缩放透射图。由于双三次插值法是根据邻域内16个像素获取插值点值，因此缩放比例scale最佳值设置为4。其他值只能小于或等于4，如果大于4，将导致上采样后的图像出现“halo”效应。

图3给出了群马图像的三种不同情况下的透射率。其中：(a)是有雾图像；(b)是无缩放和无全变分滤波处理的粗糙透射图，该透射图的纹理信息丰富；(c)是经过迭代次数为60的全变分滤波处理但无缩放处理的透射图，该透射图纹理信息较少；(d)是经过迭代次数为60的全变分滤波处理但缩放比例scale为4的缩放处理的精细透射图，该图纹理信息最少。

图3 三种不同情况下的透射图

4 实验结果和分析

根据本文算法对互联网上部分有雾图像进行去雾处理以验证本文算法的有效性和实时性，实验中的硬件和软件环境分别是：主频是1.7 GHz的四核Core i5处理器；在Windows 8操作系统上运行的MATLAB R2014b软件。

4.1 缩放比例影响

由于缩放处理可以减少全变分滤波的计算工作量，同时还具有均值滤波作用，因此缩放操作在本文算法中具有较重要的作用，缩放比例scale的设置非常关键，该值设置过大虽然均值作用明显，但“halo”现象同样严重。设置过小，全变分滤波计算量减少不够明显。根据前面的理论分析，其最佳值为4。图4给出了街景图不同缩放比例的处理结果图，其中：(a)是有雾图像；(b)的缩放比例scale为2；(c)的缩放比例scale为4；(d)的缩放比例scale为5；(e)的缩放比例scale为6；(f)的缩放比例scale为8。五种不同下采样比例恢复的图像主观视觉效果大致相近，但从白色方框标示区域的图像可以看出：缩放比例scale小于或等于4时，“halo”现象较弱，尤其是缩放比例scale为4时最弱；而缩放比例scale大于4时，“halo”现象比前两幅图像明显，缩放比例scale越大，该现象越严重。

图4 四种缩放比例的去雾结果

4.2 有效性和实时性

根据平均梯度比、新增可见边之比、熵、运行速度等客观指标以及直观视觉效果对本文算法进行了验证，并且与文献[3]算法、文献[4]算法进行对比以验证本文算法的有效性和实时性。本文算法的参数设置为：迭代次数为10，缩放比例scale为4；文献[3]算法的导向滤波半径为60；文献[4]算法的导向滤波半径为15。实验结果如图5所示，其中：第1列为有雾图像，第2列为本文算法去雾结果，第3列为文献[3]算法去雾结果，第4列为文献[4]算法去雾结果。

图5 三种算法的去雾结果

五幅图像经过图像去雾处理后视觉效果相当，图像细节比有雾图像丰富，三种算法去雾效果接近，但部分细节存在差异。文献[3]算法和文献[4]算法处理后的图像中部分物体变黑，如：文献[3]算法处理后的群马图的轮胎、公路图的垃圾桶、天鹅图的草坪和树干、广场图的大理石围栏；文献[4]算法处理后的群马图的轮胎和马脖子、公路图的部分树、广场图的树和建筑物第一楼层。而本文算法出现变黑的物体较少。

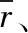
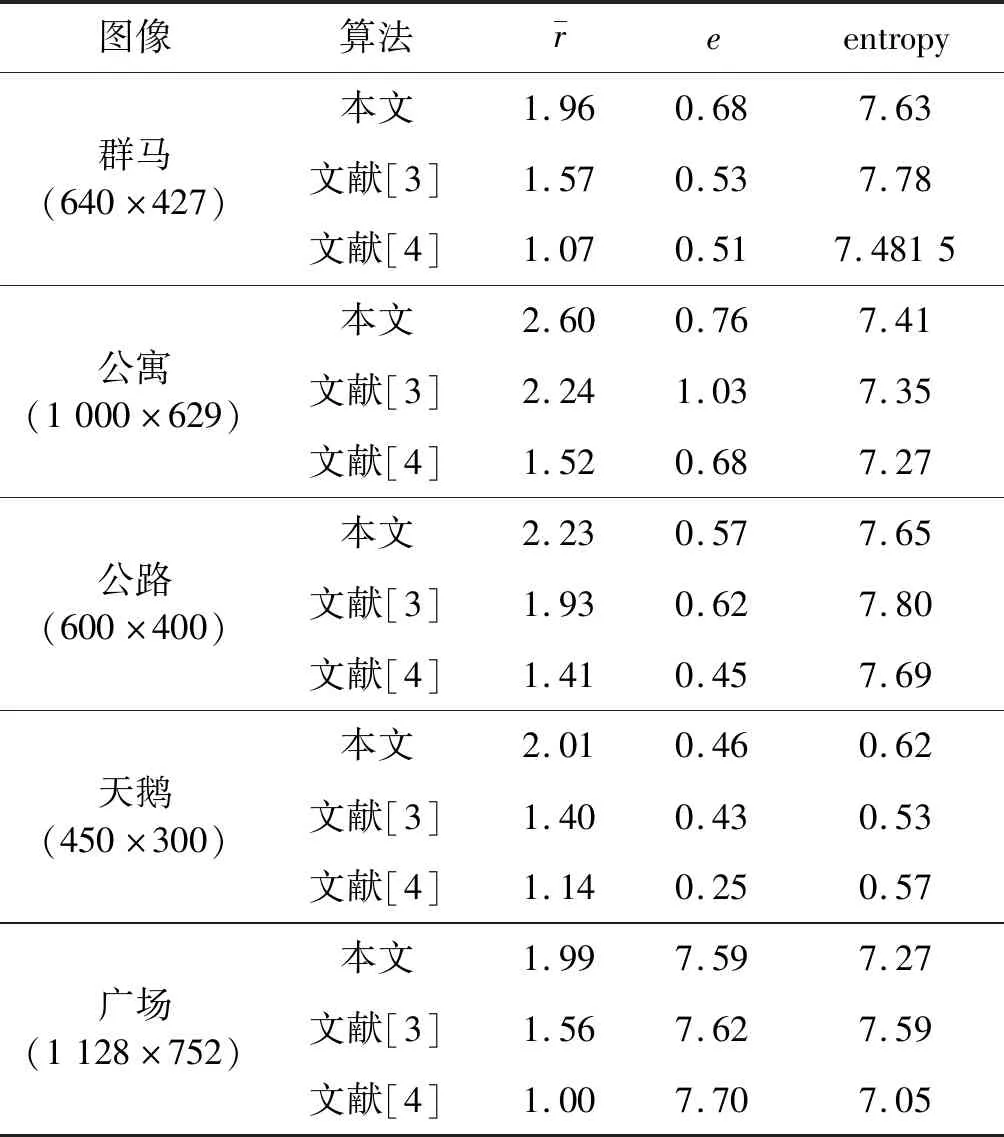
表1 三种算法的客观指标

虽然客观指标值表明三种算法客观指标相近，但表2的运行时间表明：下采样有效地减少了计算工作量，提高了去雾的速度。本文算法与文献[3]相比，最大加速比可达15.8倍，最小加速比为6倍；与文献[4]相比，最大加速比为7.2倍，最小加速比为2.7倍。图像分辨率越大，对应的加速比也越大。

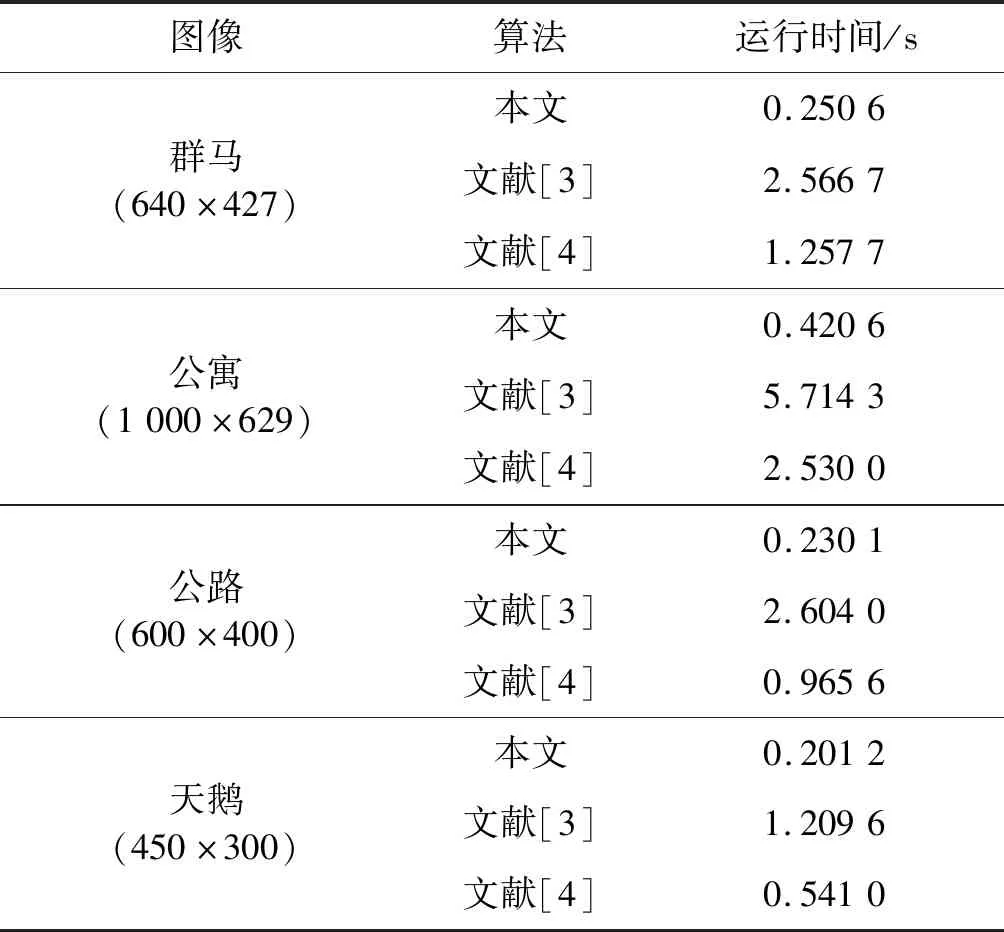
表2 三种算法的运行时间

续表2

5 结 语

本文结合最小滤波、全变分滤波提出了一种快速的单幅图像去雾算法。基于全变分的图像处理虽然可以获取较好的保边和平滑效果，但欧拉-拉格朗日方程的求解复杂繁琐，因此本文借助全变分滤波器滤除大气耗散函数中的图像纹理细节，保留与场景深度对应的景深边缘。滤波器的计算方式简单易行，只需直接使用3×3领域内的半个窗口的像素更新中心像素值即可。全变分滤波需要多次迭代导致计算耗时较长,所以采用下采样的方法降低计算复杂度。通常缩放比例越大，计算量越小，但较大的缩放比例会导致严重的“halo”效应，故本文给出了缩放比例的取值范围，小于4的缩放比例可以减少该现象。仿真结果表明：本文算法的去雾效果与其他两种算法相近，但其运行速度更快，最大加速比为15.8，最小加速比为2.7，加速比与图像分辨率成正比。因此本文算法具有较好的适应性，适合应用在对实时性要求较高的工程场合。