TOF相机的深度数据测量误差校正方法研究

王世程 于微波 杨宏韬

(长春工业大学电气与电子工程学院 吉林 长春 130012)

0 引 言

三维数据可以直观反映场景或目标的全貌信息。TOF深度相机具有结构紧凑、帧率高、对光照不敏感等优点，是一种效率较高的3D成像仪器，在三维视觉系统中应用广泛[1]。由于TOF相机自身成像特点影响以及外界不确定环境因素的扰动，导致其获得的原始深度信息附带抖动、漂移、畸变等误差[2]，最重要的深度信息难以直接应用。所以，对TOF相机获取的原始深度数据的误差进行校正尤为必要。文献[3]提出采用多采集频率的方法，以提高TOF相机的深度数据质量；文献[4]提出为每一个像素点计算相应的修正系数的方法对原始深度数据的误差进行修正，但该方法由于计算复杂度高导致消耗时间较长；文献[5]提出一种基于小孔成像原理的深度数据校正方法对原始深度数据的误差进行修正，但该方法对非系统误差校正具有一定的局限性；更多校正方法详见文献[6-8]，但依然存在诸多缺点。本文提出一种建立极限学习机(ELM)空间配准模型的方法对TOF相机深度数据测量过程中随机误差导致的深度偏移和系统性误差导致的深度数据高估进行了统一校正，并与基于BP算法[9]建立的空间配准模型和基于小孔成像原理校正的结果进行对比实验。

1 TOF相机的深度误差分析

TOF相机测量目标深度信息的原理是基于测量光在目标物体表面和传感器之间的飞行时间来计算场景到探测器像元之间的深度信息[10]。由于TOF相机自身成像特点影响以及外界不确定环境因素的扰动，导致其获取的原始深度信息存在误差。这些误差大致可分为非系统误差和系统误差。

引起非系统误差的因素一般是使用环境的差异，其中有环境的噪声、光的散射、运动模糊以及多光接收等[11]。激光是TOF相机接收的光源，由其本身提供，因此，在相同的曝光时间内，靠近相机的点容易产生过饱和现象，远离相机的点容易造成曝光不足。同时，相机发出的部分激光通过多次反射才被相机收到的现象是由于激光的散射以及漫反射造成，并且与相机距离越近，散射现象越严重。而且相机工作时间不同，芯片的温度发生变化等都可能引起深度上的漂移[2，12]。

系统误差主要是由TOF相机自身硬件系统产生的实测深度距离高于实际距离的情况。相机的球面坐标系示意如图1所示，同一物体平面Π1上有三个点A、B、C，TOF相机采集到的深度数据仅A点最接近实际深度值d。而TOF相机采集到的其他位置的深度数据如被测点B和C到相机O的直线距离分别为rB和rC。通常，这种直线距离rB或rC总是大于垂直实际距离d，即被测点B和C的深度信息被过高估计。同理，对于平面Π2上测得的类似位置的深度数据情况也是如此。

图1 TOF相机的球面坐标系示意图

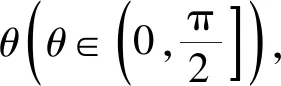
(1)

由式(1)得出，当角度θ一定时，随着真实距离的增加，偏差ΔD与D存在一种线性递增的关系；当真实距离为D一定时，随着角度θ的增加，偏差ΔD与角度θ存在一种非线性递增的关系。

在实际测量中，当相机以光轴垂直物体平面的方式拍摄时，越靠近镜头的光轴中心对应的物体平面待测位置的点时，则越接近实际的垂直距离d。而远离镜头的光轴中心对应的物体平面待测位置的点，即处在镜头视角边缘处的点，就会被系统性地高估。这种高估对后续图像的三维重建以及处理都会产生很大影响。

2 深度误差修正的ELM空间配准模型

TOF相机非系统和系统误差的叠加导致的数据偏移与真值之间存在某种非线性的规律，且很难用精确的数学模型进行描述，因此可以采用机器学习算法对其进行处理。本文使用建立极限学习机(ELM)空间配准模型的方法对TOF相机的深度误差进行校正。

2.1 点云数据采集

用TOF(tof640-20gm_850nm)深度相机垂直照射墙面，实验设备环境图如图2所示。

图2 实验设备环境图

为了降低随机误差的影响，开机40 min预热后，在保持相机平面与墙面平行，且相机平面与墙面垂直距离的1.0～4.5 m范围内的状态下，每隔10 cm采集10幅相应位置的深度数据并过滤掉非0的像素后，求平均深度值zm，而该位置到墙的实际距离zc已知。以zm和zc为依据，确定采样间隔为1 cm对相邻深度数据帧各个对应像素位置的zm和zc的值分别在z轴方向进行三次样条插值[13]处理。z轴方向样条函数如下所示：

(2)

进而得到近似连续又满足实际要求的离散空间照片的深度数据p(xm,ym,zm)和相应的实际垂直距离信息zc，为后续TOF相机深度数据ELM空间配准模型的建立做好数据准备。

2.2 ELM算法原理

极限学习机(ELM)的网络结构[14]如图3所示。设输入层的输入变量个数为n,隐含层的神经元个数为l,输出层的m个神经元则对应m个输出变量,w为输入层与隐含层间的连接权值，β为隐含层与输出层间的连接权值，b为隐含层神经元的阈值。

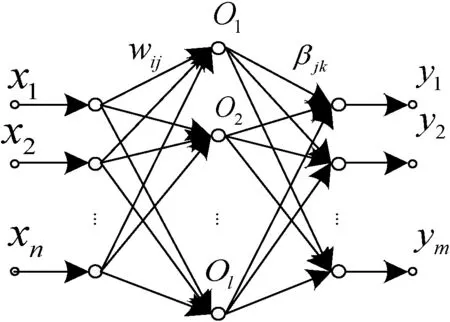
图3 单隐层前馈神经网络结构

将输入层第i个神经元与隐含层第j个神经元之间的连接权值表示为wij，隐含层第j个神经元与输出层第k个神经元间的连接权值表示为βjk,则:

(3)

假设训练集有Q个样本，其输入矩阵X和输出矩阵Y分别为：

(4)

设g(x)为隐含层神经元的激活函数，则网络的输出T为：

T=(t1,t2,…,tQ)m×Q

(5)

式中：j=1,2,…,Q，wi=[wi1,wi2,…,win]，xj=[x1j,x2j,…,xnj]T，则式(5)可表示为：

Hβ=T′

(6)

式中：矩阵T′为T的转置；H为隐含层输出矩阵。

H(w1,w2,…,wl,b1,b2,…,bl,x1,x2,…,xQ)=

(7)

在训练前，随机选取输入层和隐含层之间的连接权值w以及隐含层神经元的阈值b，并且训练过程中它们保持不变。H+为H的广义Moore-Penrose逆矩阵，利用它可以求得满足零误差逼近的β。

(8)

ELM算法的建模步骤如下：

1) 随机产生神经网络的输入层和隐含层之间的连接权值w以及隐含层神经元的阈值b；

2) 计算隐含层输出矩阵H；

3) 通过输出矩阵H的广义逆矩阵H+求得输出连接权值β。

2.3 ELM配准模型建立步骤

应用ELM算法建立TOF相机深度数据空间配准模型步骤如图4所示。

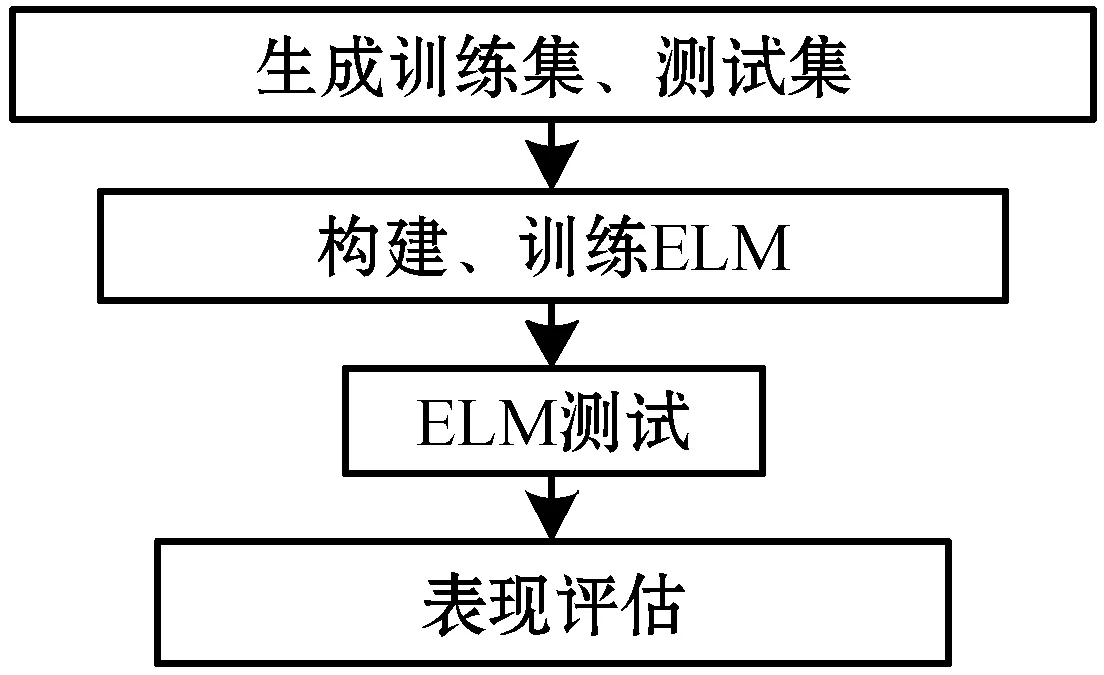
图4 ELM建模步骤

1) 以三次样条插值函数得到的p(xm,ym,zm)和zc为依据，将TOF深度相机在各个空间位置上对应的像素深度值p(xm,ym,zm)和理想深度值zc作为训练集，任意选取几幅不同空间位置的深度图像的原始深度数据p(xm,ym,zm)和对应的zc，并加入随机噪声信号作为测试集。

2) 构造ELM模型结构，确定输入层的3个输入变量p(xm,ym,zm)，根据训练样本数确定隐含层神经元个数，确定1个输出变量zc。通过训练建立测量值p(xm,ym,zm)和实际深度值zc之间的非线性映射模型。对于建立成功的ELM空间配准模型，将对近似连续空间内所有像素的深度数据起到相应的校正作用。

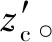
3 实验结果与分析

3.1 实验仿真结果

本实验使用ELM算法和BP算法分别构建的空间配准深度数据校正模型以及基于小孔成像原理校正的三种方法进行实验并对比。实验数据采集范围为1.0～4.5 m，选取深度相机实际测量得到的2.0 m的深度数据图像作为实验展示。原始数据点云如图5所示；基于ELM算法空间配准模型校正后数据点云如图6所示；基于BP算法空间配准模型校正后数据点云如图7所示；基于小孔成像原理校正后数据点云如图8所示。直观上来说，图5中的原始数据点云很凌乱，而图6-图8中校正后的数据点云相对平整，说明三种方法对原始数据点云都有大幅度的校正，而各方法之间的校正结果并不明显。故需要对各方法之间的校正结果做进一步比较分析。

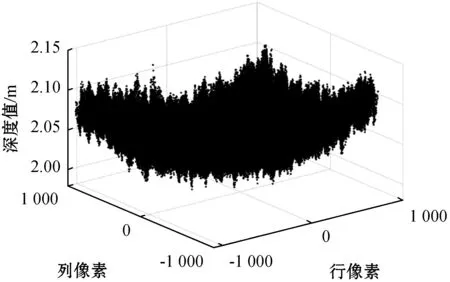
图5 原始数据点云图

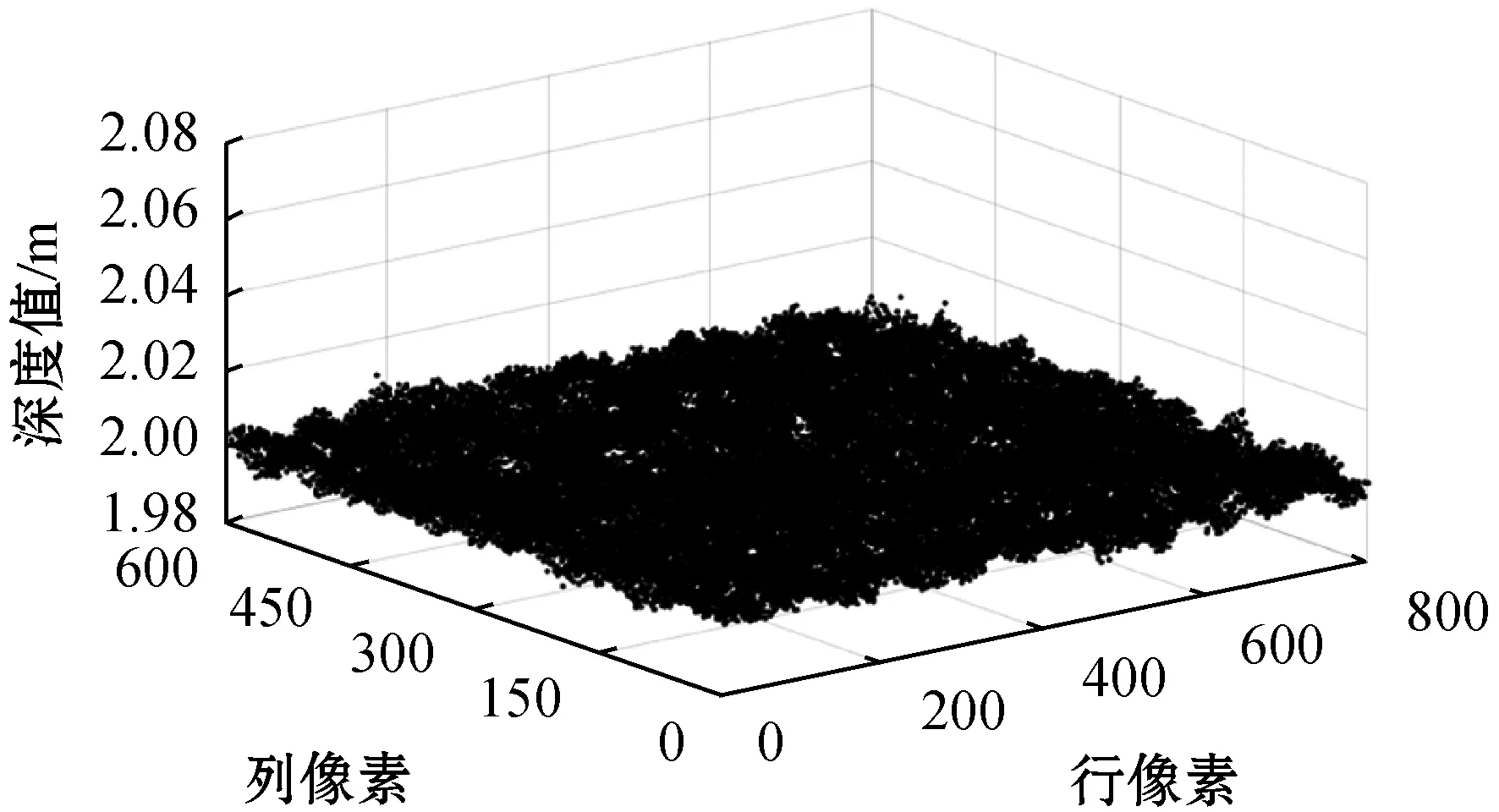
图6 基于ELM算法空间配准模型校正后数据点云图

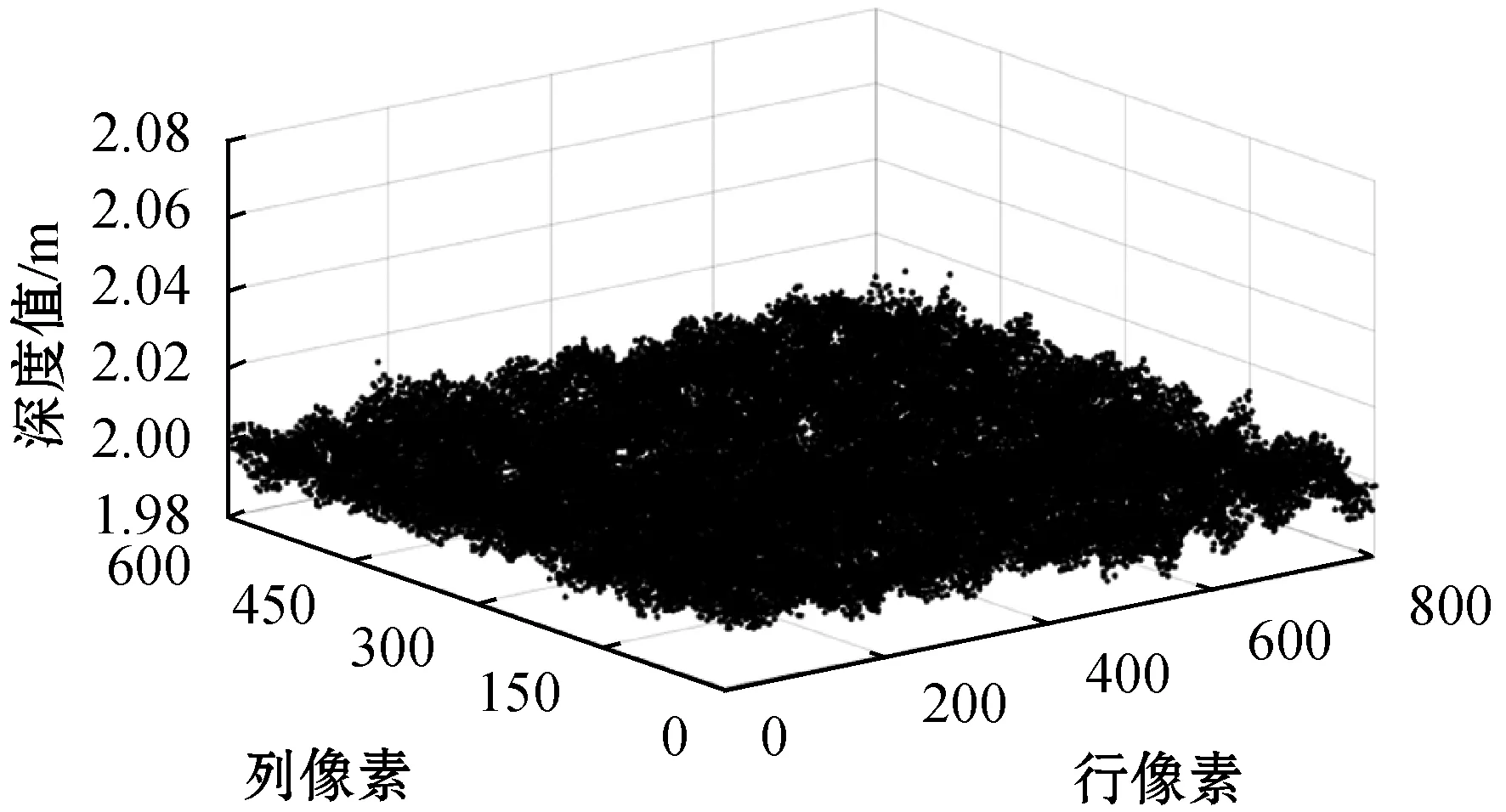
图7 基于BP算法空间配准模型校正后数据点云图

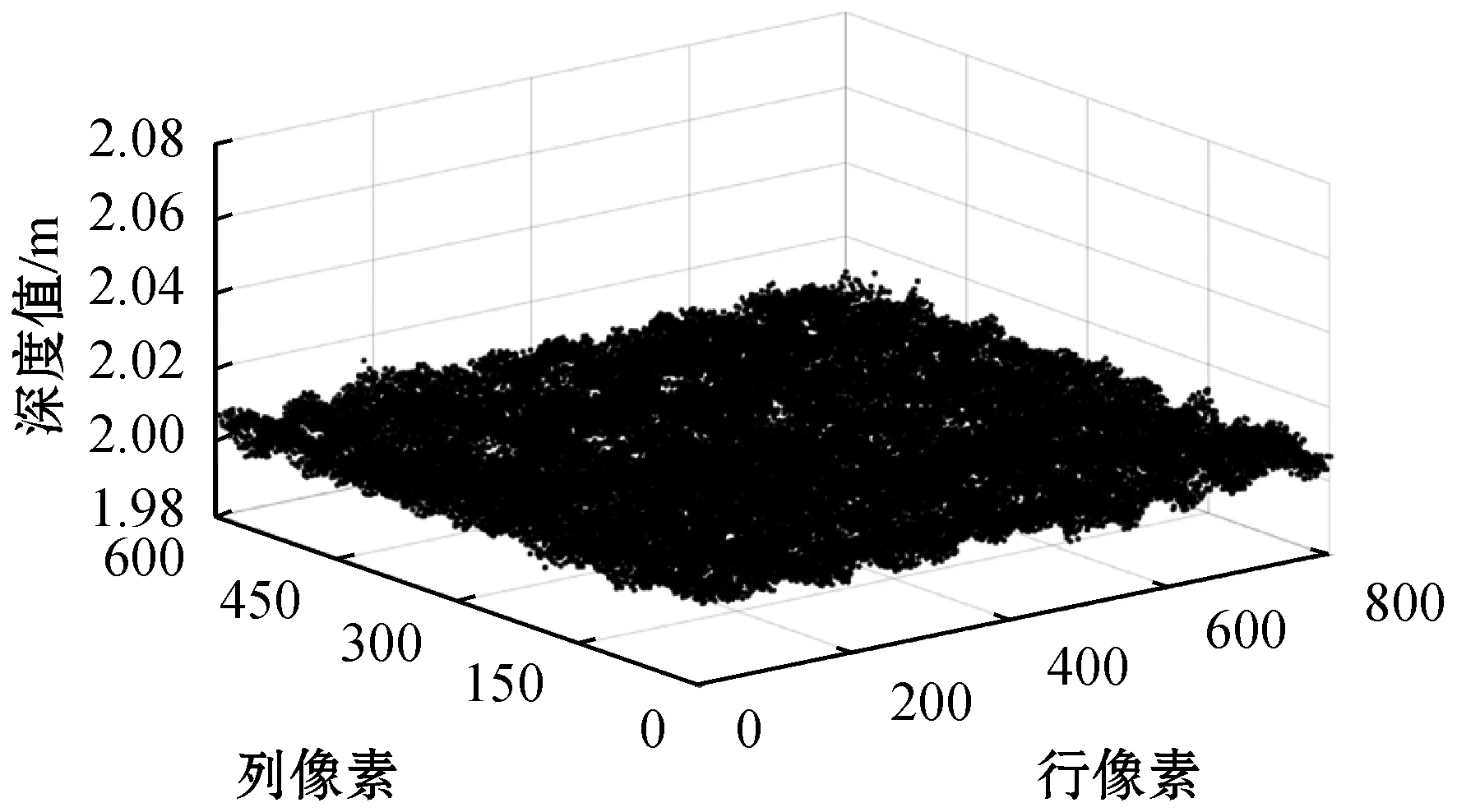
图8 基于小孔成像原理校正后数据点云图

3.2 实验结果分析

对上述三种方法的校正结果进行分析，校正结果验证对比如图9所示。可以看出，基于ELM算法空间配准模型校正后的深度值曲线更加收敛于实际理想深度值曲线。

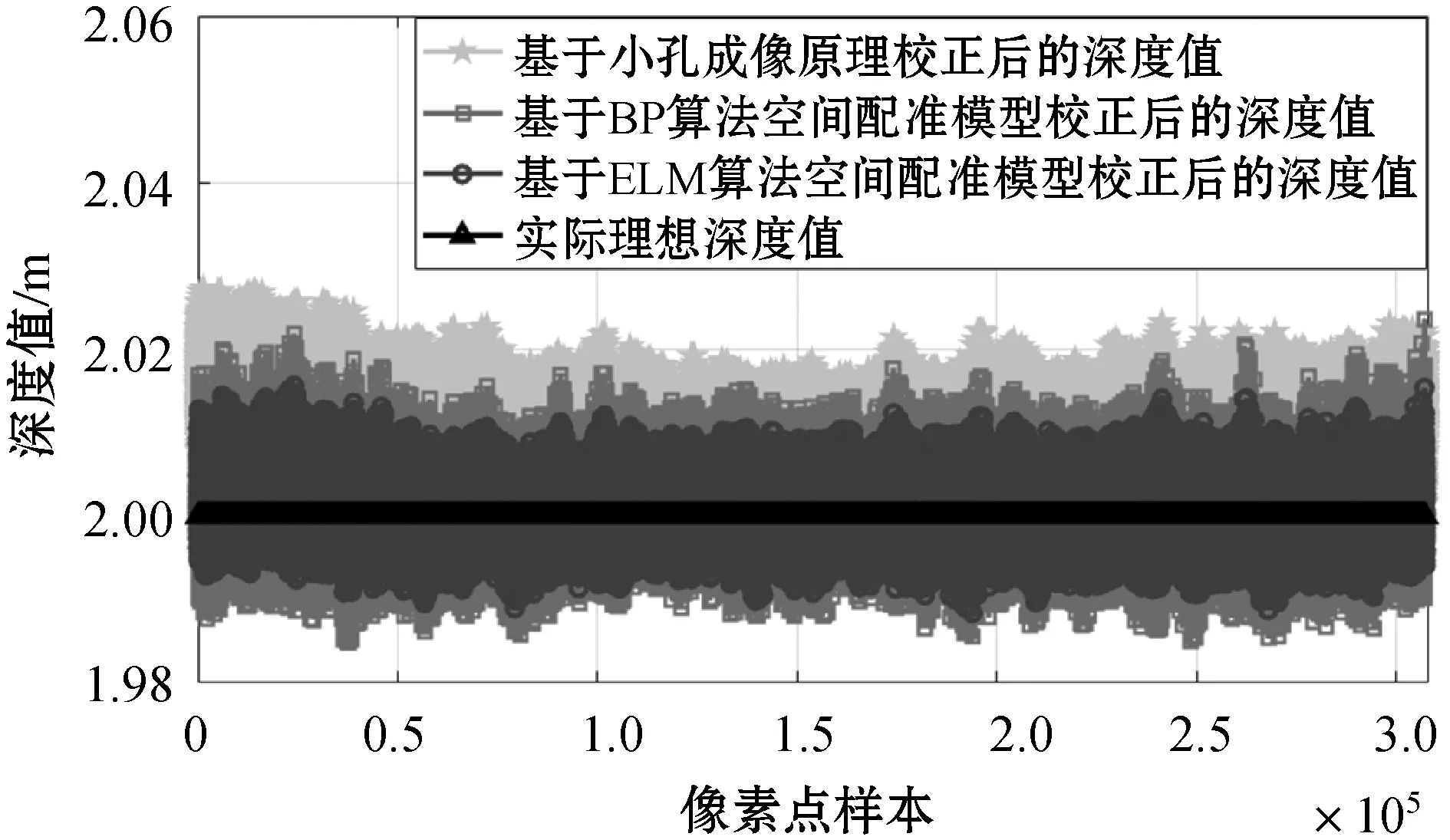
图9 校正结果验证对比图

相对误差对比如图10所示。可以看出，基于小孔成像原理、基于BP算法空间配准模型和基于ELM算法空间配准模型校正后的深度值相对误差曲线在零值附近的振荡幅度与原始相对误差相比都大幅减小，说明三种方法对原始误差都有较大幅度的改善，并且基于ELM算法空间配准模型校正后的深度值相对误差曲线在零值附近的振荡幅度更小。

图10 相对误差对比图

对测量距离为2.0 m的一幅深度数据的各像素进行定量分析，三种方法对单幅深度数据处理效果对比结果如表1所示。其中：基于ELM算法空间配准模型校正后的平均绝对误差是基于BP算法空间配准模型校正后的69%左右，是基于小孔成像原理校正的31%左右；均方根误差是基于BP算法空间配准模型校正后的70%左右，是基于小孔成像原理校正的34%左右。ELM算法空间配准模型、BP算法空间配准模型和基于小孔成像原理校正的平均相对误差分别为0.13%、0.18%和0.41%。而且基于ELM算法建立的空间配准模型对单帧各像素深度数据的处理速度比基于BP算法建立的空间配准模型速度更快，与基于小孔成像原理校正方法耗时相当。因此，基于ELM算法建立的TOF相机深度数据空间配准模型校正效果更好。

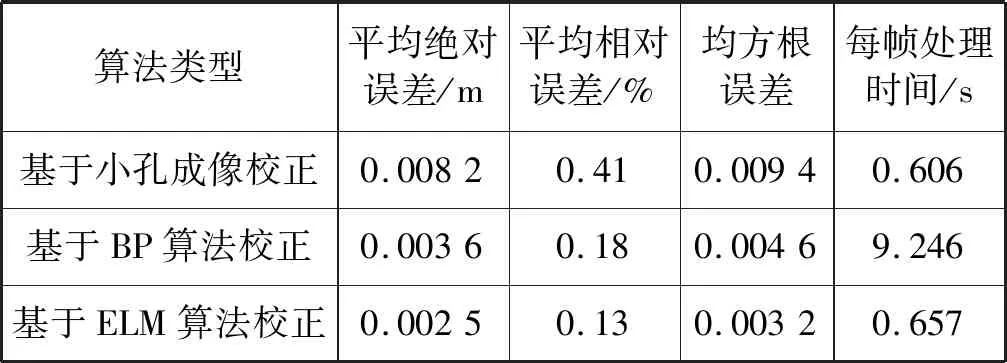
表1 三种方法对单幅深度数据处理效果对比列表

对测量范围为1.0～4.5 m的采样间隔为1 cm的351帧深度数据图像进行分析。图11显示了深度空间方向对应空间位置原始数据的平均绝对误差与三种方法校正结果的平均绝对误差。

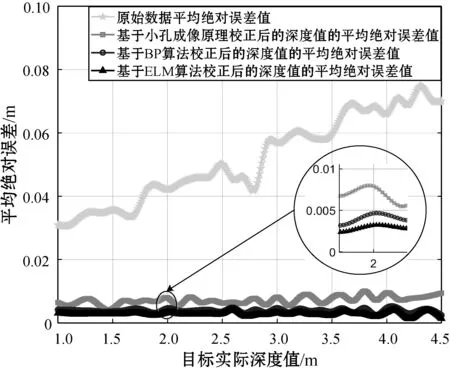
图11 平均绝对误差对比图

由图11的局部放大图可以看出，经三种方法校正后的深度值的平均绝对误差值与原始误差相比都大幅减小，说明这三种方法对原始误差都有较大幅度的改善。从图11全局来看，基于ELM算法校正后的深度值的平均绝对误差值曲线在零值附近的振荡幅度更小。

三种方法处理各深度空间位置对应深度数据的平均绝对误差如表2所示。从表中数据很容易得出，ELM算法空间配准模型校正后的平均绝对误差是基于BP算法空间配准模型校正后的71%左右，是基于小孔成像校正的33%左右。所以，基于ELM算法空间配准模型比基于BP算法空间配准模型和基于小孔成像原理校正方法对实验范围的深度数据校正的总体效果都好，其总体结果更接近实际理想深度值。

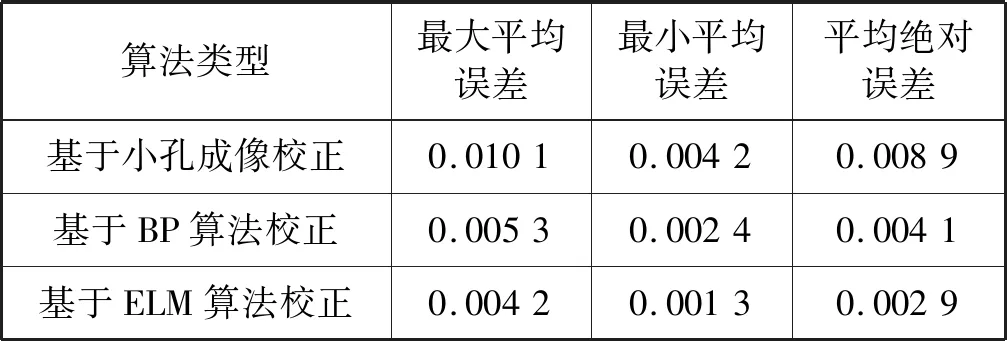
表2 平均绝对误差对比列表 m

4 结 语

本文提出的基于极限学习机(ELM)空间配准模型的方法对TOF相机深度数据测量过程中非系统性和系统性误差的叠加导致的深度数据偏移进行了统一校正，并与基于BP算法建立的空间配准模型和基于小孔成像原理校正的结果进行对比，分析得出ELM算法空间配准模型校正的平均绝对误差是基于BP算法空间配准模型校正的71%左右，是基于小孔成像原理校正的33%左右。实验结果表明，采用ELM算法建立的ELM空间配准校正模型大幅减小了TOF相机测得的实验范围内的深度数据帧的误差。基于ELM算法建立的空间配准模型比基于BP算法建立的空间配准模型和基于小孔成像原理校正方法对实验范围的深度数据帧校正的总体效果都好，能更好地复原真实场景中的深度数据。