基于遗传算法的SVM自适应干扰样式选择

戴少怀，王 磊，李 旻，余 科，罗 晨

(上海机电工程研究所，上海 201109)

0 引 言

随着人工智能算法被应用于作战雷达，雷达的抗干扰性能及认知性能不断提升，致使常规的干扰方式不能发挥应有的电子战效能，因此需要加快推进干扰技术的发展[1]。自适应干扰技术作为认知电子战的关键技术，干扰决策的实时性和干扰样式匹配准确率是自适应干扰的重要指标。文献[2]采用模式识别的方法，将雷达工作模式分为扫描模式和跟踪模式，并采取两种不同的压制干扰对雷达目标实施干扰，该方法的优点是实现简单，缺点是参数固化，只采用压制性干扰，自适应选择的自由度不够。文献[3]采用博弈论的思想进行雷达干扰决策生成，实现非确定条件下的干扰样式选择；文献[4]采用基于多决策准则的思想，综合考虑不同准则，通过投票法实现最终干扰决策，这两种方法基本能实现干扰样式的最优选择，但是选择自由度和实时性不足。文献[5]提出了一种基于干扰效果库和干扰样式库对相控阵雷达实施智能干扰的决策系统，通过不断修正期望值来进行干扰样式选择，该方法能够有效提高干扰决策系统对雷达信号的自适应能力，但实时性也不高。文献[6]提出基于支持向量机(SVM)算法的干扰样式选择策略，采用GS法对SVM算法参数优化，干扰样式匹配的准确率和干扰决策的实时性不高。上述方法存在自适应选择自由度不足、实时性不高等问题，在实际应用中难以满足工程需求。

本文以相控阵雷达为例，对雷达工作模式进一步划分，研究不同模式下雷达最优干扰样式，提出一种用于自适应干扰样式选择的IGA-SVM算法，提高干扰决策的准确率和实时性。采用IGA对SVM算法中惩罚参数和核函数参数进行优化，然后将侦察的雷达信号特征数据作为测试集，验证改进优化方式后算法模型的学习能力和泛化能力，提高在雷达不同工作模式下自适应干扰决策的准确率和实时性。

1 针对相控阵雷达的干扰样式选择

1.1 干扰样式选择准则

干扰设备对雷达实施干扰和雷达采用抗干扰措施进行反干扰是一个相互矛盾、动态博弈的过程。为保证干扰设备对雷达实施有效干扰，干扰方在选择干扰样式时需要综合考虑待干扰雷达的工作模式及其可能采用的抗干扰措施，从而确定自身应采用的最优干扰样式。因此，需要选择和雷达工作状态相匹配的干扰样式，才能获得预期的最佳干扰效果。

通过对典型电子作战战例、外场电子对抗试验和电子对抗数字仿真试验结果的研究、分析和总结，本文基于文献[7-9]从对抗的针对性、干扰设备可承受能力和干扰技术可实现度等角度进行了分析，初步设定干扰样式选择准则如下：

1) 从适应战场环境广、需要同时干扰的雷达数量和体制种类多、响应快速的要求出发，可优先选择时域、频域宽开的非相参干扰，压缩对雷达信号进行侦察和分析处理的时间，确保对处于战场不同位置的雷达都能做到干扰信号与目标回波同时到达雷达。如在远距离支援干扰和随队掩护干扰的情况下，干扰设备资源充裕，优先采用压制性干扰。

2) 从适应雷达信号多变的要求出发，可优先选择仅需侦收雷达信号粗略参数的压制性干扰，避免因对雷达数据库过度依赖而丢失最佳干扰时机。如针对雷达的捷变频、脉冲参数参差和欺骗脉冲等抗干扰措施，优先选择频域覆盖范围较宽、时域持续时间较长、功率谱密度较高的压制性干扰。

3) 在干扰机发射功率充裕的条件下，从降低目标被雷达发现概率的干扰目的出发，可提高干扰/信号功率比，优先选择压制性干扰，如噪声调频干扰、密集假目标等干扰样式。

4) 在干扰机发射功率有限的条件下，从增大雷达对目标测量误差、饱和雷达信号处理能力、消耗雷达资源的干扰目的出发，优先选择欺骗性干扰，也可避免因大功率压制干扰信号而暴露干扰平台信息的问题。如在自卫干扰条件下，干扰方首选多假目标、距离欺骗、速度欺骗、角度欺骗、航迹欺骗等干扰样式。

1.2 针对相控阵雷达的最优干扰样式选择策略

现代地空导弹制导雷达多采用平面相控阵技术，具有很高的测角和测距精度，同时拥有很强的抗干扰能力，其工作模式可以分为搜索模式、跟踪模式和识别模式。

相控阵雷达在不同工作模式下具有不同的信号特征，对雷达信号进行特征提取，可以识别相控阵雷达的工作模式，根据1.1节内容，得出简化的干扰样式选择策略如下：

1) 相控阵雷达处于远距离搜索模式时，优先采用压制式干扰，大功率压制信号可以淹没真实目标回波，使对方雷达探测系统无法探测目标。相控阵雷达处于近距离搜索模式时，优先采用假目标密集复制干扰，欺骗干扰可产生多个假目标，使对方雷达无法获取真正目标的参数信息或饱和其雷达信号处理系统。

2) 相控阵雷达处于跟踪模式时，表明雷达已经发现并锁定了真实目标。为降低雷达对真实目标的威胁，可以采用拖引式干扰。常见的拖引式干扰有速度拖引、距离拖引和距离速度同步拖引，这里采用距离拖引的方式，欺骗对方雷达距离自动跟踪系统，使雷达丢失真正的目标信息。

3) 相控阵雷达处于成像识别模式时，对目标的威胁程度增加。为破坏对方雷达对己方真正目标信息的有效快速识别，不仅需要考虑雷达的工作状态，还需要侦收雷达抗干扰措施相关信息，针对不同情况采用不同干扰样式。如当雷达采用捷变频抗干扰措施时，可以采用宽带阻塞干扰；采用数字射频存储工作体制时，可采用灵巧噪声干扰。

综合以上分析，针对相控阵雷达的不同工作模式，干扰样式选择策略如图1所示。

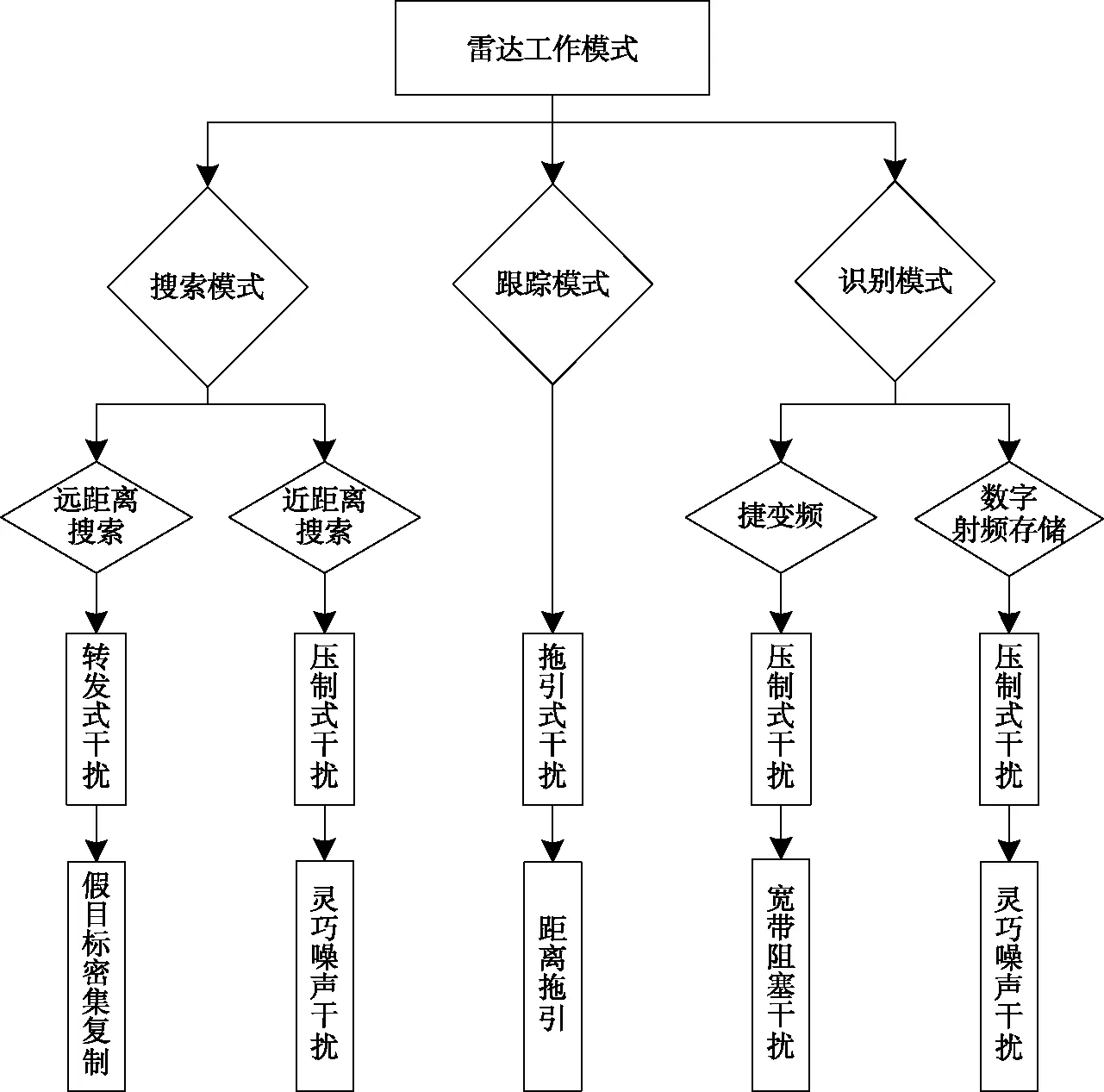
图1 雷达干扰样式选择策略Fig.1 Radar jamming mode selection strategy

2 GS-SVM算法原理及其分析

2.1 SVM算法

支持向量机是一种基于统计学理论的新型学习机，具有很好的学习能力和泛化能力。SVM算法是由线性可分的二分类问题发展而来，其基本模型是定义在特征空间上的间隔最大的线性分类器，基本思想是建立一个高维特征空间中的最优超平面,以最大间隔距离将两类样本分开。

以二分类问题为例，分析SVM算法基本原理:设一线性可分的训练样本集为T={(x1,y1),(x2,y2),…,(xm,ym)}，决策分类面方程为〈ω·x〉+b=0。其中：xi为第i个样本；yi为样本xi对应类别，二分类问题中yi取1或者-1，分别代表两个不同类别H1和H2；ω和b分别代表权值向量和偏置。以最大分类间隔区分两类样本，找到最优超平面，决策面和最近样本点之间的距离为分类间隔ρ=2/‖ω‖，可将此问题转化为线性约束的凸优化问题，其目标函数为

(1)

综合以上分析，可以采用Largrange乘子法解决线性约束的凸优化问题，引入Largrange函数

(2)

式中：α=[α1,…,αm]Τ为Largrange乘子且大于0。将Largrange函数分别对权值ω和偏置b求偏导置零，代入原函数，将问题转化为对偶问题

对式(3)优化问题进行求解，可以得到

(4)

代入分类超平面方程可得决策分类面为

〈x·ω*〉+b*=0

(5)

在工程中,实际遇到的很多问题都是线性不可分问题，此时需要对SVM算法进行处理，基本思路是通过定义核函数将线性不可分问题映射为高维特征空间的线性可分问题，处理流程如下：

1) 针对线性不可分数据，为每个样本引入松弛变量ξi和惩罚参数C，使部分样本可以位于间隔区域内或者决策面另一侧，此时式(1)可以表示为

(6)

式中：松弛变量ξi非负；惩罚参数C表示对间隔误差的容忍度，其值较大意味着加大对间隔误差的惩罚力度，较小则说明对间隔误差容忍度高。

2) SVM将输入空间的非线性问题转化为特征空间的线性问题，可以通过定义核函数K(xi·xj)建立输入空间到高维空间的隐映射，在输入空间内积运算，再映射到高维，避免了高维内积计算。同线性可分问题，利用Largrange乘子法将问题(5)转化为其对偶问题

(7)

核函数K(xi·xj)需要满足Mercer条件，才可以实现从非线性问题到特征空间线性可分问题的转化。常见的核函数有线性核函数、多项式核函数、径向基核函数和sigmoid核函数。径向基核函数具有较好的时效性和鲁棒性，是应用最广泛的核函数。这里选取径向基作为核函数进行分析，其核函数可表达为

K(xi,xj)=exp(-g|xi-xj|2)

(8)

式中：g为核函数参数。

根据式(7)～(8)可知，惩罚参数C和核函数参数g的取值直接影响SVM分类准确率，参数组合(C,g)的取值是模型优劣的关键。

2.2 GS-SVM算法复杂度分析

对组合参数优化，最常用的方法是GS法，其基本思路是首先确定参数C和g的取值范围，然后选择合适的参数寻优步长，构建参数组合(C,g)的二维网格平面。在SVM模型训练过程中，遍历每一组参数组合，找到使模型误差最小的参数C和g作为最优组合。若参数寻优范围与搜索步长选取合适，就可保证模型有较高的准确率和运算效率。若步长过小，虽能提高参数优化精度，但算法效率低；若步长过大，参数易跳过最优取值，优化精度不够。因此，为减小搜索步长对模型的影响，在进行干扰决策时，拟通过改进遗传算法对SVM算法参数进行优化，提高干扰决策的实时性和准确率。

3 IGA-SVM算法

3.1 GA的改进及SVM参数优化

遗传算法(GA)是模拟生物进化论的自然选择和遗传机理的算法模型，通过选择、交叉变异等操作，实现种群进化。遗传算法进行优化时，主要以种群适应度作为搜索导向，优胜劣汰，不断更新种群，从而快速寻找全局最优解。

在遗传算法中，参数交叉率和变异率直接影响算法优化效果。交叉率越大，染色体更新速率越快，但较优的染色体也易被破坏，难以达到全局最优；交叉率越小，搜索过程就越缓慢，算法效率越低。对变异率而言，其取值过大，遗传算法会变成随机搜索，无法收敛；变异率过小，则无法产生有效的新染色体。文献[10]采用遗传算法对SVM算法参数进行优化，固定交叉率Pc和变异率Pm，优化效果较好，但算法搜索缓慢，迭代时间较长。为保证交叉率和变异率在进化过程中取值适中，设计了如式(9)所示的方法来确定交叉率和变异率。

(9)

式中：P1、P2分别表示初始交叉率和初始变异率；ti，tm分别表示当前进化代数和总进化代数。这种改进能保证在进化过程中交叉率和变异率始终保持在合理范围，保证优化精度的同时提高收敛速度。

采用IGA优化组合参数，以干扰样式匹配的准确率为目标函数，优化惩罚参数和核函数参数组合，具体步骤如下：

1) 采用二进制编码方式对种群初始化。C∈(0～102)，g∈(0～103)，随机产生惩罚参数C和核函数参数g的组合，作为初始种群；

2) 将种群基因串由二进制转换成十进制，代入IGA-SVM算法模型，进行训练和测试；

3) 计算各个体的适应度函数值；

4) 终止条件判断：满足终止条件退出循环，得到两个参数的最优组合结果，否则执行5)；

5) 执行选择，优胜劣汰，留下适应度高的个体，淘汰适应度低的个体；

6) 根据式(9)确定交叉率和变异率，进行交叉变异操作，不断更新种群，增强种群多样性，返回执行2)。

3.2 干扰样式自适应选择模型

利用IGA寻找SVM算法中惩罚参数和核函数参数的最优组合，将优化后得到的IGA-SVM算法作为自适应干扰样式选择器。侦察雷达信号并提取信号特征参数，形成训练集对IGA-SVM算法模型进行训练，将待干扰雷达信号特征作为测试集，利用训练好的IGA-SVM算法实现干扰样式最优选取。其基本过程如下：

1) 选取雷达特征参数，形成训练样本集；

2) 归一化处理特征向量，防止不同参数之间的差异导致模型训练产生偏差；

3) 利用样本集对IGA-SVM算法模型进行训练；

4) 对待干扰信号进行特征提取；

5) 将待干扰信号特征数据作为IGA-SVM算法模型的输入，进行干扰样式的自适应选择；

6) 输出干扰样式，释放干扰信号；

7) 再次进行雷达信号侦察和特征提取，利用侦察到的数据进行干扰效果评估；

8) 根据侦察数据和评估结果，再次调整输出相应的干扰样式。

图2为基于IGA-SVM算法的自适应干扰样式选择流程。

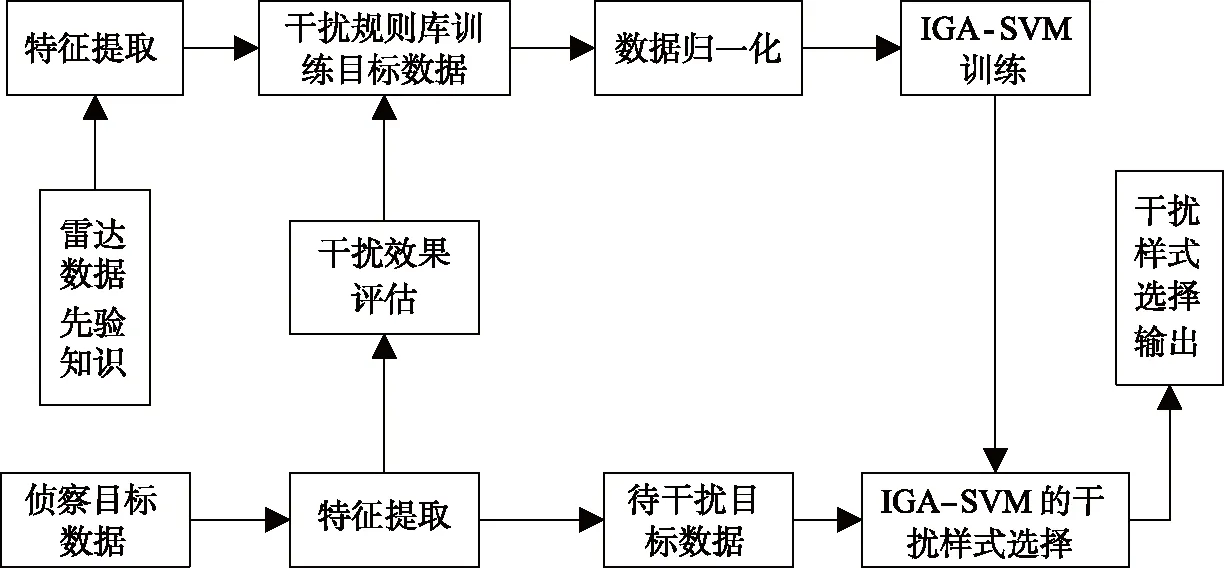
图2 IGA-SVM算法的自适应干扰样式选择流程Fig.2 IGA-SVM adaptive interference mode selection process

4 仿真结果及其分析

为验证IGA-SVM算法模型进行干扰样式自适应选择的有效性，针对某X波段相控阵雷达，侦察其雷达信号并进行特征提取，以所提取雷达数据的一部分作为训练集，对IGA-SVM模型进行训练，另一部分作为测试集。在雷达工作过程中，重频、载频等参数将在一定范围内变化。在测试集中添加10dB的高斯白噪声，验证模型对测试集信号特征干扰样式匹配的准确率。两种优化方法的测试结果对比如表1所示。

表1 两种优化方法的测试结果对比Tab.1 Comparison test results of two optimization methods

由表1可以看出，IGA-SVM自适应干扰样式选择结果明显优于GS-SVM。从干扰样式匹配的准确率上看，在2 000个测试样本集情况下，IGA-SVM算法模型干扰样式匹配准确率达到96.7%，而GS-SVM模型干扰样式匹配准确率为92.3%。从运行时间上看，IGA-SVM算法寻找最优参数组合消耗时间明显短于GS-SVM模型，一定程度上解决了干扰样式匹配准确率低、实时性差等问题。

基于Matlab仿真平台，分别利用IGA和GS法对SVM算法模型中惩罚参数C和核函数参数g进行寻优，并将优化后的参数组合代入训练模型，利用测试集对模型进行测试，所得结果分别如图3～5所示。

采用IGA进行参数优化时，种群个体适应度和进化代数之间的关系曲线如图3所示。经历30次迭代后，个体最佳适应度达到最大值且保持稳定，此时参数C和g的最佳组合为{C=76.172，g=1.288}。将优化结果代入SVM算法模型并训练，然后将测试集2 000个样本作为输入，得到IGA-SVM模型干扰样式匹配结果如图4所示。由图4可看出IGA-SVM算法模型干扰样式匹配的准确率为96.7%，其运行时间为0.061 259 s。

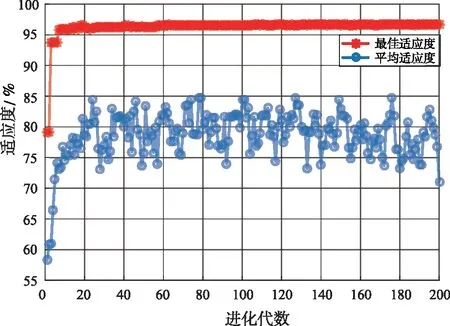
图3 IGA优化参数适应度变化曲线Fig.3 The fitness curve of IGA optimized parameters

图4 IGA-SVM干扰样式匹配结果Fig.4 Interference mode matching result of IGA-SVM

采用GS法对SVM算法进行参数优化，得到最优参数组合为{C=388.023，g=0.574}，将同一测试集2 000个样本代入GS-SVM算法模型，得到干扰样式匹配结果如图5所示。由图5可得GS-SVM干扰样式匹配准确率为92.3%，运行时间为0.138 973 s。

图5 GS-SVM干扰样式匹配结果Fig.5 Interference mode matching result of GS-SVM

5 结束语

本文提出了一种改进遗传算法优化的SVM模型,用于干扰样式自适应选择。针对传统方法存在的干扰决策实时性差、干扰样式准确率不高等问题，以模型干扰样式匹配准确率为目标，采用IGA对SVM组合参数进行优化，实现干扰样式的自适应选择。仿真结果表明：IGA-SVM模型在干扰决策的实时性和干扰样式匹配准确率方面均优于GS-SVM算法模型，具有较强的学习能力和泛化能力，为自适应干扰技术提供了有力支撑。