一种基于滑动铰点的快速起竖方法及优化设计

2020-07-12王兰志李书新

空天防御 2020年2期

王兰志,李书新

(1. 北京航天发射技术研究所，北京 100076；2. 中南大学航空航天学院，湖南长沙 410083；3. 首都航天机械公司，北京 100076)

0 引言

在现代化战争领域，随着高新技术的不断引入，战争突发性和速决性骤然增强，对导弹的机动性和快速反应能力有了更高的要求[1]。导弹发射车的无依托发射能力使导弹的机动性得到了很大的提高。为了在复杂的作战环境中提高导弹武器系统的快速反应能力，获得作战的主动权，快速起竖系统成为提高导弹武器系统快速反应能力的有效手段。

根据调研结果，目前我国现有的起竖系统与国际先进水平相比还存在着很大差距[2-5]。高新技术的发展，使得多电化乃至全电化逐渐成为未来技术发展的趋势[6]。在“全电驱”趋势的牵引下，起竖缸推力已不再是限制起竖装置的根本问题，起竖缸行程、伸缩比成为快速起竖装置发展的瓶颈。

传统的起竖系统广泛使用三铰点机构。三铰点机构由质量载荷和起竖油缸组成，起竖油缸下支点连接车体，上支点连接质量载荷，使载荷绕一个起竖铰点旋转起竖，如图1所示。

图1 三铰点起竖机构Fig.1 Three-hinge-point erecting mechanism

三铰点起竖机构有着结构简单、操作便捷的优点，在起竖系统中被广泛使用。但它存在执行机构行程长、导向比大的缺陷，在大型设备的起竖过程中往往使用多级缸以减小起竖系统所占空间，这不仅加大了生产成本，换级带来的振动冲击更是对起竖过程中的稳定性带来极大的影响。并且，执行机构的长行程制约了起竖速度的提高。

结合起竖系统的设计特点，本文通过起竖缸上端采用滑动铰点的方法解决大质量货物快速起竖的问题，起竖机构方案如图2所示。该机构主要功能是实现大质量货物从水平状态起竖到竖直状态，再从竖直状态撤回至水平状态。

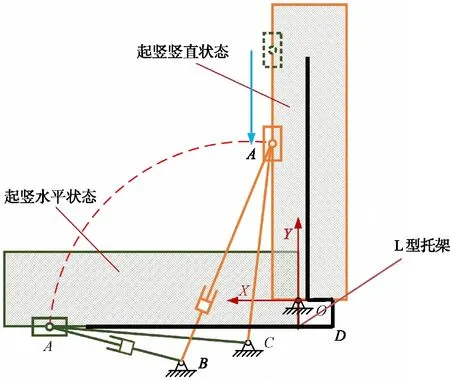
图2 大质量货物滑动铰点起竖机构方案示意图Fig.2 Scheme of erecting mechanism of sliding hinge point for heavy goods

可以看出，该起竖机构具有1个独立的驱动杆，用以驱动载荷绕基准点O的起竖运动。和传统的三铰点起竖机构相比，该机构的特殊之处在于将L型托架底部的铰点A变固定为可沿直线移动，同时增加了一个摇杆AC用于支承载荷和限定机构自由度。

1 基于滑动铰点的快速起竖方法建模

根据大质量货物滑动铰点起竖机构总体方案，建立滑动铰点起竖机构解算模型，如图3所示。建立坐标系OXY并设置各点坐标，设摇杆AC长度为p，起竖缸AB长度为l，D点为L型托架转折点(OD与DA垂直)，滑动铰点A距D点长度为d，θ为起竖角，h为O点距D点长度，G为质量载荷的重量。

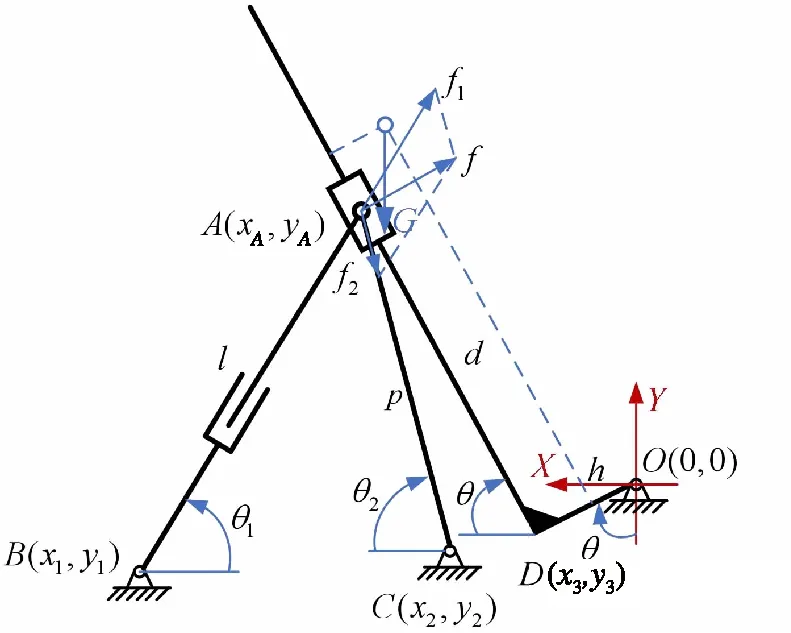
图3 滑动铰点起竖机构解算模型Fig.3 Solution model of the erecting mechanism with sliding hinge point

首先根据几何关系求取滑动铰点A坐标为

(1)

得到方程

(2)

则起竖缸行程为

(3)

在起竖角θ=0°时，起竖缸初始长度记为lin，在θ=90°时起竖缸最终长度记为len，则起竖缸行程l为

l=len-lin

(4)

滑动铰点行程距离为

(5)

同理，滑动铰点A滑动行程AD为

AD=den-din

(6)

式中：den为起竖角度为90°时A、D之间的距离；din为起竖角度为0°时A、D之间的距离。

在不考虑摩擦的情况下，起竖缸和摇杆合力与导轨垂直，根据力矩平衡，合力为

(7)

式中：xG0、yG0分别为水平状态载荷x方向和y方向的坐标。

根据图3解算模型，可得如式(8)所示关系。

(8)

求解得到起竖缸推力f1和摇杆拉力f2分别为

(9)

2 起竖机构优化设计

2.1 边界条件

考虑到起竖机构在实际工作过程中受到的约束，作出如下假设：

(1) 大质量货物质量60 t，质心在起始位置坐标已知；

(2) 起竖缸下支点最低不超过2 280 mm，即x1≤2 280 mm；

(3) 摇杆下支点最高到车体上平面，即y2≥-1 600 mm；

(4) 上支点距离回转中心距离不小于1 241 mm，即h≥1 241 mm；

(6) 整个过程中，滑块导向行程不超过6 000 mm；

(7) 摇杆长度尽量小，小于7 000 mm；

(8)x1、x2、x3的值在10 000 mm范围内。

2.2 优化模型求解

通过以上几何关系和力学模型，结合边界条件输入，可将本机构优化问题转化为一般的非线性优化问题。

最优化问题的一般形式为

(10)

式中：x={x1,x2,…,xn}T；F:Rn→R1；ci:Rn→R1；x为决策变量；F(x)为目标函数；ci(x)(i=1，2，…,p)为约束函数。

首先，优化目标为寻找起竖缸最小载荷的情况下，到位上支点尽量靠近质心，且确保起竖缸最大载荷要求不大于130 t。将此优化问题等效为在满足几何关系、质心约束等条件下的油缸载荷最大化问题进行求解。

其中，必要的约束为

(11)

利用Matlab工具箱中的fmincon函数可求解以上非线性约束条件下目标函数的最优解。将最优化问题转化为

(12)

式中：优化变量x=(x1,h1,x2,h2,h3,m)T，含6个参数变量。

(13)

根据上述优化模型进行求解，最终得到的优化结果为

x=[5 908,-2 378,2 834,-1 546,-1 193,5 805]T

(14)

起竖缸收缩长度为2 962.2 mm，伸出长度为7 949.5 mm，摇杆长度为5 805 mm，初始位置起竖缸受力129.3 t，能够满足边界条件。

2.3 优化结果分析

根据优化结果及解算模型，建立如图4所示的起竖机构三维模型，主要由大质量货物、基座、起竖缸、摇杆、滑动铰点等组成。

根据载荷分布及结构设计可知，整个起竖系统对称布置，为方便起见，在进行动力学建模分析时，将起竖机构简化为平面机构进行分析。在多体动力学仿真软件ADAMS中添加驱动和约束后，对起竖过程进行动力学仿真，如图5～7所示。

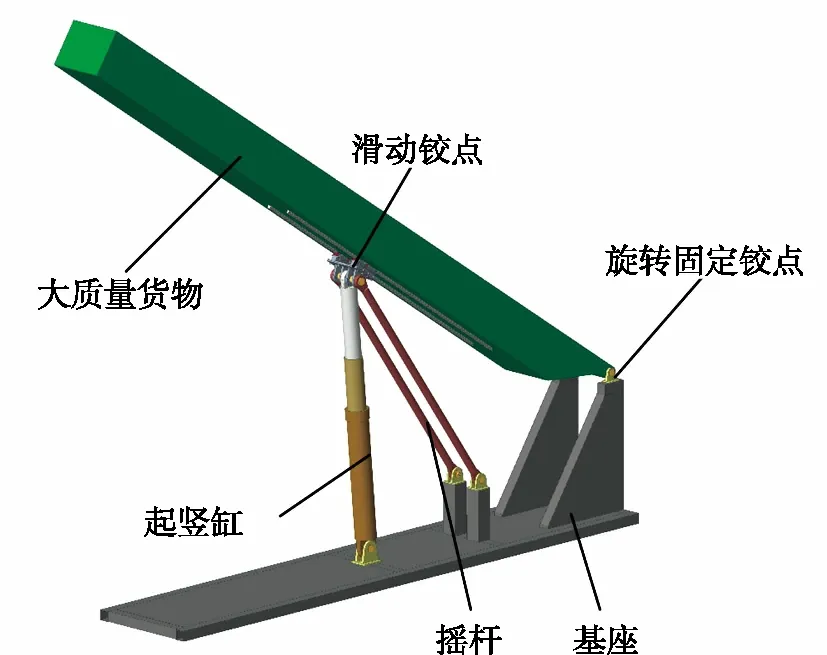
图4 起竖机构三维示意图Fig.4 Three dimensional schematic diagram of erecting mechanism

图5 摇杆受力随时间变化曲线Fig.5 Rocker force curve changing with time

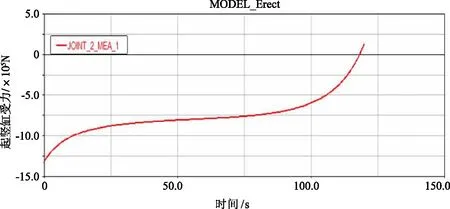
图6 起竖缸受力随时间变化曲线Fig.6 Erecting cylinder force curve changing with time

图7 滑动铰点受力随时间变化曲线Fig.7 Sliding hinge point force curve changing with time

由图5可以看出，摇杆受力随时间变化由拉力变为压力，最大拉力为60.95 t，最大压力7.04 t。由图6可以看出，起竖缸受力随时间变化由压力变为拉力，最大压力132.80 t，最大拉力13.55 t。由图7可以看出，滑动铰点受力随时间变化由压力变为拉力，最大压力44.86 t，最大拉力4.49 t。

对比理论计算结果进行分析，可得理论计算结果和仿真分析结果中各杆件受力趋势相同，数值在可允许误差范围内，由此可知计算结果正确。