基于正交偶极子阵列的混合信号波达方向与极化参数联合估计

王嘉宁，司伟建，乔玉龙

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

0 引 言

波达方向估计技术始终是信号处理领域的研究热点之一，被广泛应用于现代通信与电子对抗等诸多领域。在电子对抗领域，现有的传感器阵列主要可分为标量传感器阵列与矢量传感器阵列两种。矢量传感器阵列具有易于与载体表面共形、抗干扰能力强、能够估计辐射信号的极化信息等诸多优势，从而得到了广泛的研究并产生了诸多的研究成果[1-4]。一些基于标量传感器的算法，例如传播算子(propagator method, PM)算法[5]、多重信号分类(multiple signal classification, MUSIC)算法[6]与旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法[7]也都在极化敏感阵列上得到了直接的推广应用。然而需要指出的是，这些算法正确推广的前提是入射信号中仅仅包含不相关信号。当入射信号为相干信号，或者是由不相关信号与相干信号混合而成的混合信号时，阵列接收数据的协方差矩阵会产生秩亏损，从而导致导向矢量与噪声子空间不再正交，此时传统的PM算法、MUSIC算法与ESPRIT算法皆会失效。为了解决这一问题，相关研究人员提出了空间平滑算法与矩阵重构算法[8]，用于消除信号间的相关性。空间平滑算法利用子阵列接收数据的平滑性去消除信号间的相关性。矩阵重构算法将协方差矩阵元素或协方差矩阵大特征值对应的特征矢量的元素进行重新排列，直接构造新的协方差矩阵。这两类方法以损失阵列孔径为代价实现了解相干。采用空间平滑算法与矩阵重构算法，子空间类算法可以实现标量传感器阵列下的相干信号的角度估计，然而这两类解相干算法不能直接在矢量传感器阵列下进行推广。

为了解决极化敏感阵列下相干信号的估计问题，XU首先提出了极化角平滑算法(polarimetric angular smoothing algorithm, PAS)[9]，利用全电磁矢量传感器的6个通道之间接收数据的自相关矩阵的平均来恢复数据协方差矩阵的秩。随后HE基于极化角平滑算法提出了极化差分平滑算法[10]，这类极化平滑算法要求所选用的矢量传感器必须为全电磁矢量传感器，并且能够分辨的相干信号的个数至多为6个。TAN将极化平滑与广义MUSIC算法相结合,用于实现对低空目标的角度估计[11]。真实环境中，由不相关信号与相干信号混合而成的混合信号普遍存在，对于标量传感器阵列下的混合信号的角度估计已经有了一定的研究成果[12-14]，然而在矢量传感器阵列下的混合信号角度与极化联合估计算法的研究成果较少，因此研究极化敏感阵列下混合信号的角度估计问题具有一定的理论价值。现有的极化敏感阵列下混合信号的估计算法[15]中的角度估计方法实质上为ESPRIT算法，没有充分利用阵列接收的数据，采用子空间类的角度估计算法能够进一步提高角度估计的精度。此外，现有的一些极化敏感阵列下相干信号的角度估计算法，例如极化角平滑算法与极化差分算法，没有充分利用全电磁矢量传感器各个分量接收数据之间的相关性实现混合信号的极化参数估计。

为了解决上述的问题，本文基于正交偶极子阵列提出了一种新颖的极化敏感阵列混合信号角度与极化参数联合估计算法，本文算法的贡献主要包含以下几个方面：

1) 利用正交偶极子阵列代替原来的全电磁矢量传感器，降低了天线的硬件消耗，消除了全电磁矢量传感器各个阵元间的互耦引入的误差；

2) 所提算法不仅可以实现混合信号的入射角度估计，还可以实现对混合信号极化参数的估计；

3) 所提算法消除了噪声的干扰，通过扩展传播算子得到正交子空间，采用子空间类的算法提高了角度估计精度。

1 信号模型

正交偶极子均匀线阵阵列如图1所示。

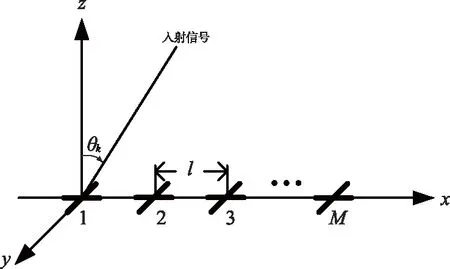
图1 正交偶极子均匀线阵阵列Fig.1 Uniform line array of orthogonal dipoles

假设存在K个入射角度为{θk}、极化信息为{γk,ηk}、波长为λ的窄带远场混合信号{sk(t)}(k=1,2,…,K)入射到由M个正交偶极子所组成的阵元间距为l的均匀线阵阵列上。这K个混合信号由Ku个不相关信号与Kc个相干信号组成，这Kc个相干信号可以分为D个相干组，且每个相干组包含{Pd}(d=1,2,…,D)个相干信号。此时整个阵列输出的2M×1维矢量可以表示为

(1)

式中：{sd(t)}(d=1,2,…,D)为第d个相干组的相干源信号；第d个相干组中的第p个入射角度为θd,p的信号与相干源信号sd(t)之间的相关系数为ζd,p；N(t)为叠加在阵元上的高斯白噪声数据矩阵；阵列的导向矢量a(θk,γk,ηk)为空域导向矢量q(θk)与极化导向矢量c(θk,γk,ηk)的克罗内特积，如式(2)所示。

a(θk,γk,ηk)=q(θk)⊗c(θk,γk,ηk)

(2)

式中:

q(θk)=[1,e-j2πlsinθk/λ,…,e-j2π(M-1)lsinθk/λ]T

(3)

c(θk,γk,ηk)=[-cosγk,cosθksinγkejηk]T

(4)

将式(1)改写为矩阵的形式,为

X(t)=Au(θ,γ,η)Su(t)+Ac(θ,γ,η)ΓSc(t)+N(t)=A(θ,γ,η)ES(t)+N(t)

(5)

阵列总的输出协方差矩阵可以表示为

(6)

2 混合信号的参数估计

2.1 不相关信号的参数估计

图2给出了正交偶极子均匀线阵阵列分割示意图。

图2 正交偶极子均匀线阵阵列分割示意图Fig.2 Schematic diagram of array segmentation of orthogonal dipole uniform line array

将图1所示的正交偶极子均匀线阵阵列分割为两个相互重叠的分别包含M-1个正交偶极子阵元的子阵1与子阵2，则这两个线性子阵列的输出分别可以表示为

(7)

式中：下标1和2分别代表两个子阵；矩阵A1为阵列总的导向矢量矩阵A的前2(M-1)行；B=blkdiag{Bu,Bc,1,…,Bc,D}，Bu=diag{e-j2πlsinθ1/λ，…，e-j2πlsinθKu/λ}，Bc,d=diag{e-j2πlsinθd,1/λ，…，e-j2πlsinθd,Pd/λ}；X1(t)与N1(t)为X(t)与N(t)的前2(M-1)行；X2(t)与N2(t)为X(t)与N(t)的后2(M-1)行。

根据以上的定义，子阵1的自协方差矩阵可以表示为

(8)

子阵2与子阵1之间的互协方差矩阵可以表示为

(9)

式中，矩阵RN形式为

(10)

(11)

(12)

(13)

(14)

(15)

将式(15)代入式(11)可得

(16)

化简可得

RAA1Γ=A1BΓ

(17)

式(17)可以被写为

RA[A1u,A1c，1ζ1,…,A1c,DζD]=[A1uBu,A1c，1Bc,1ζ1,…,A1c,DBc,DζD]

(18)

式(15)中包含了目标矩阵与不相关信号导向矢量A1u以及每个相干组的导向矢量A1c,d之间的联系，本文算法的核心便是利用式(18)实现混合信号的角度以及极化参数估计。

接下来定义矩阵RAo与RAe分别为矩阵RA的奇数行和偶数行

(19)

式中：A1o为矩阵A1的奇数行；A1e为矩阵A1的偶数行。取RAo1为RAo的前Km行，其中Km=Ku+D，RAo2为RAo的后M-1-Km行，则(M-1-Km)×Km维线性算子Pu定义为

(20)

Pu可由式(21)获得。

(21)

(22)

从式(22)可以看出矩阵Qu的列矢量张成的空间与导向矢量A1o的列矢量张成的空间相互正交，正交传播算子Gu可以写为

(23)

Gu的行组成的矢量与导向矢量A1o的列组成的矢量之间仍满足正交关系

GuA1o=O(M-1)×Km

(24)

依据阵列总的导向矢量矩阵A，可以将A1o写为A1o=[Au1o,Ac1o]，其中Au1o与Ac1o分别为矩阵Au与Ac的前2(M-1)行中的奇数行。由此可得

(25)

不相关信号导向矢量Au的列张成的空间与相关信号导向矢量AcΓ的列张成的空间的交空间为零空间，因此我们可以通过求取式(26)的最小值来得到不相关信号的θ角的估计值

(26)

式中，qu(θ)=[1,e-j2πlsinθk/λ,…,e-j2π(M-2)lsinθk/λ]T。至此，我们得到了不相关信号的角度估计结果。由式(19)可知矩阵RAe同样可以用于不相关信号的角度估计。依据前面的流程可以再次对不相关信号的入射角度进行估计，我们取两次估计结果的均值为最后的不相关信号的角度估计结果。接下来我们给出不相关信号的极化信息的估计方法。

对矩阵RA执行奇异值分解，即可得到矩阵A1、B的估计值，依据已经估计出的角度结果，即可获得与第k个不相关信号对应的导向矢量a1(θk,γk,ηk)，a1(θk,γk,ηk)为矢量a的前2(M-1)行，且满足

a1(θk,γk,ηk)=q1(θk)⊗c(θk,γk,ηk)

(27)

(28)

(29)

式中，a1k(2i)为矢量a1k的第2i个元素。

2.2 相关信号的参数估计

在完成不相关信号的角度估计后，我们可以得到矩阵A1，从而可以得到Ac1o的估计值。矩阵Ac1o的第d(d=1,2,…,D)列可以写为

(30)

式中，Cco,d为Cc,d的第1行，Cc,d=[cd,1,cd,2,…,cd,Pd]。为了消除每个相干组中相干信号之间的相干性，将对应于第d个相干组的阵列流形矢量Ac1o,d中的元素进行重新排列，构建一个(M-Pd-1)×(Pd+1)维的矩阵Ho,d，如式(31)所示。

(31)

当M-Pd-1≥Pd+1时，Ho,d为满秩矩阵，并且可以改写为如式(32)的形式。

ΦoΞ

(32)

式中，Ac,d为Ac中第d个相干组的导向矢量的前M-1-Pd行。

取Ho,d的前Pd行得到矩阵Ho,d1，取Ho,d其余的M-2Pd-1行得到矩阵Ho,d2，将第d个相干组的重构矩阵Ho,d对应的传播算子Pco,d定义为

(33)

Pco,d可由式(34)获得,即

(34)

(35)

Gco,d的行与Ac,d的列之间满足正交关系

Gco,dAc,d=O(M-Pd-1)×Pd

(36)

依据子空间正交性原理，我们可以通过求取式(37) 的最小值来得到第d组相干信号的估计值

(37)

ΦeΞ

(38)

式中，Cce,d为Cc,d的第2行。对矩阵He,d采用上面相同的方法再次得到第d个相干组的角度估计结果。将两次角度估计结果取均值，作为第d个相干组的相干信号的最终角度估计结果。接下来我们讨论每个相干组中相干信号的极化参数的估计。由于Cco,d与Cce,d分别为Cc,d的第1行与第2行，因此必存在一个包含极化信息的矩阵Jd，且满足Ho,dJd=He,d。根据最小二乘理论，有

(39)

在式(39)两侧对矩阵Jd求偏导，可得

(40)

当上式的值为0时，可得Jd的解为

Jd=((Ho,d)THo,d)-1(Ho,d)THe,d=(Ho,d)†He,d

(41)

将式(29)、(35)代入式(41)中，可得

(42)

(43)

式中，μd,p=-cosθd,ptanγd,pejηd,p,p=1,2,…,Pd。由式(43)可以看出第d个相干组中相干信号的极化信息隐藏在矩阵Jd的特征值中。对矩阵Jd执行特征分解，通过特征值匹配操作使得每一个μd,p与入射角θd,p一一配对，则第d个相干组中的极化信息可以表示为

(44)

(45)

对每个相干组皆可以采用以上的方法估计出其所对应的入射角度与极化信息，最终得到完整的混合信号角度与极化信息估计结果。

3 仿真实验分析

本章通过仿真实验来验证本文所提出的算法有效性。仿真实验的实验条件如下：

1) 图1中所示的正交偶极子均匀线阵阵列两个相邻阵元间的阵元间距被设置为入射信号波长的一半，即l=λ/2；

2) 信噪比(signal to noise ratio，SNR)定义为信号的功率与所叠加噪声功率的比值；

3) 角度θ的均方根误差(root mean square error，RMSE)被定义为

(43)

选取文献[9]中的PAS算法、文献[15]中的算法作为本文算法的对比算法。

仿真实验1：比较各个算法在不同信噪比下的角度估计能力。在本实验中假设存在两个不相关信号源：不相关信源1的入射角度、极化辅助角与极化相位差分别为(55.17°,50.43°,14.13°)；不相关信源2的入射角度、极化辅助角与极化相位差分别为(33.18°,30.78°,50.24°)。假设存在一组包含两个相关信号的相干信号源：相干信号源1的入射角度、极化辅助角与极化相位差分别为(14.26°,30.41°,12.27°)；相干信号源2的入射角度、极化辅助角与极化相位差分别为(-2.33°,13.26°,29.52°)，且这两个相干信源间的相干系数为ζ=[1,ejπ/3]T。阵元数M被设置为8，信噪比SNR从0 dB开始以1 dB为间隔增至20 dB，快拍数为128。在每个仿真条件下做1 000次蒙特卡洛独立重复性试验，得到不相关信源入射角度θu的均方根误差RMSEθu,如图3所示，得到相干信源入射角度θc的均方根误差RMSEθc,如图4所示。

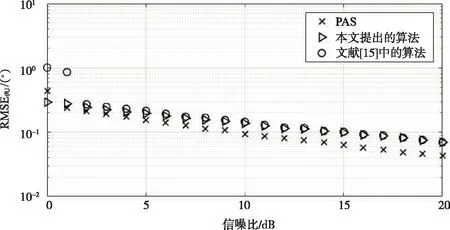
图3 不相关信号角度估计均方根误差随信噪比变化曲线Fig.3 Curve of RMSE of uncorrelated signal angle estimation versus SNR

图4 相干信号角度估计均方根误差随信噪比变化曲线Fig.4 Curve of RMSE of coherent signal angle estimation versus SNR

从图3～4可以看出，对于不相关信号角度估计性能，本文提出的算法与文献[15]提出的算法差别不大。而PAS算法优于其余两种算法，这是由于PAS算法要求每个阵元为全电磁矢量传感器，每个阵元包含6个通道，PAS算法通过对这6个通道接收数据的自相关矩阵进行加权求和来实现解相干。理论上PAS算法最多可以估计6个信号，然而本文提出的算法仅要求每个阵元包含2个通道，在保证估计精度的同时，极大地降低了硬件资源的消耗与计算复杂度。对于相干信号的角度估计性能，本文提出的算法要优于文献[15]提出的算法。这是因为一方面我们在算法最初进行了去噪处理，另一方面本文中对相干信号的角度估计算法可以理解为一种正交子空间方法，而文献[15]中选用的方法为ESPRIT方法。

仿真实验2：比较各个算法对极化信息的估计效果。由于PAS算法并不能估计极化信息，所以我们仅仅比较本文算法与文献[15]中的方法对混合信号的极化信息的估计效果。在实验1的仿真条件下，取信噪比SNR为10 dB。通过绘制100次本文提出算法与文献[15]中算法对极化信息的估计结果散点图来直观地进行比较，分别如图5和图6所示。

图5 本文算法对混合信号的极化信息估计结果散点图Fig.5 The scatter diagram of the polarization information estimation result of the mixed signal by the proposed algorithm

图6 文献[15]中的算法对混合信号的极化信息估计结果散点图Fig.6 The scatter diagram of polarization information estimation of the mixed signals by the algorithm in Ref. [15]

从图5～6可以看出，文献[15]提出的算法对极化信息的估计效果要优于本文提出的算法，这是由于本文提出的算法对子阵列进行了划分，损失了阵列孔径，所以对极化信息的估计效果略差。

4 结束语

本文基于正交偶极子极化敏感阵列提出了一种混合信号的角度与极化联合估计算法。首先构造目标矩阵，依据子空间方法估计不相关信号的入射角度，利用正交偶极子阵列接收数据的相关性估计出不相关信号的极化参数，在估计的过程中角度信息与极化信息可直接实现正确的配对。而后对特征矢量重新排列，估计出每个相干组的入射角度，利用最小二乘法估计出每个相干组的极化参数。与现有的针对全电磁矢量传感器的算法相比，所提出的算法降低了硬件资源的消耗，并且实现了对极化信息的估计，提高了可估计的混合信号的数目。与现有的同类算法相比，本文提出的算法提高了对相干信号的角度估计精度。仿真实验验证了本文算法的有效性与可靠性。