想象·描述·画图:培养学生空间观念的渐进途径
2020-07-11
(闽清县白中镇普贤小学,福建 福州 350806)
对小学生而言,空间观念就是他们对客观事物的空间形式进行观察、分析和抽象所形成的一种能力,是学生对大脑中已有表象加工或改造的一种能力。[1]空间观念是客观事物在学生大脑中所留下的表象;空间表象是学生形成空间观念的基本材料。空间观念包括空间感(大脑中的三维映像或平面图形的三维视觉化)、实物几何化、空间几何结构的二维表示以及由此形成的空间结构关系等。[2]《义务教育数学课程标准(2011 年版)》要求学生学会“根据几何图形想象出所描述的实际物体”“描述图形的运动和变化”“依据语言的描述画出图形等”。培养学生的空间观念离不开想象、描述和画图。教师要引导学生充分经历想象、描述和画图过程,循序渐进地培养他们的空间观念,使他们的空间观念不断得到发展和提升。
一、想象实际物体
想象是培养学生空间观念的重要思维活动之一。小学生的几何思维主要体现在自身的直观感受和已经形成的图形表象。由几何图形想象实际物体就成为学生学习几何知识的基本活动之一。空间想象是一种直觉,是学生对客观事物的空间形式所进行的一种观察、分析、抽象思考和构造创新的心理过程,[3]是学生对物体形状、结构、大小和位置关系的想象。学生必须借助一定的经验和具体材料进行想象,想象才有据可依,才更为理性。借助表象进行想象是小学生形成空间观念的重要途径之一。小学生可以根据几何图形想象客观事物的具体形状与大小,可以根据图形之间的关系想象彼此之间的转化过程,也可以根据展开图想象几何体的具体形状,还可以根据不同角度所看到的视图想象几何体的具体形状。
如教学“长方体和正方体”时,人教版小学数学教科书五年级下册有这样一道习题:把长26 厘米、宽18厘米的长方形纸,从四个角各剪去一个边长4 厘米的正方形(如图1),再折成一个无盖的长方体纸盒。这个纸盒的容积是多少立方厘米?教师可以引导学生根据题目所描述的信息想象实际物体的形状和大小。学生经过独立思考和小组交流,发现长方形纸的长边剪去2 个小正方形后,剩下26-4-4=18 厘米,宽边剪去2 个小正方形后,剩下18-4-4=10 厘米,这两条边相当于长方体底面的长和宽,剪去小正方形的边长相当于长方体的高。这样,长方体纸盒的容积就是18×10×4=720 立方厘米。
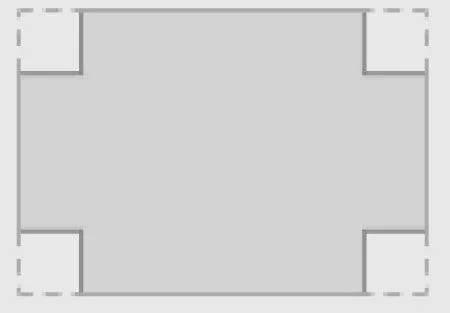
图1
通过想象,学生可以积极、主动、自觉地在二维展开图和三维几何图形之间建立联系,实现二维图形和三维图形之间的相互转换,在大脑中形成一个长18 厘米、宽10 厘米、高4 厘米的长方体表象,这不仅是他们的思考过程,也是他们借助表象展开心理操作的过程。在这样的想象过程中,学生对长方体基本元素之间的空间结构关系有了清晰认识,他们的空间观念就会由感知逐渐上升为一种可以把握的能力。
二、描述运动变化
生活中有很多图形的运动和变化现象,这些现象中总有一些是不变的。在图形的运动和变化中发现变与不变是小学生发展空间观念的关键,也是他们学习图形运动和变化内容的价值所在。小学数学教科书中,“图形的运动与变化”主要包括轴对称图形、图形的平移和旋转以及图形的放大和缩小等几个知识点。教学这些知识点时,教师要引导学生在观察、比较和交流中主动发现并描述图形在运动过程中的变与不变、如何变以及图形运动、变化前后各部分之间的对应关系,帮助他们形成相应的空间表象,使学生在探索和理解变与不变的过程中认识图形之间的关系、逐渐形成空间观念。
如教学“圆柱和圆锥”时,学生经常常常会遇到把平面图形旋转成立体图形的习题,如:把一块底是6 厘米、高是8 厘米的直角三角形硬纸板分别绕它的两条直角边旋转一周,能形成两个大小不同的圆锥。你能分别算出它们的体积吗?解决问题时,学生可以通过小组合作的方法旋转一面直角三角形小旗,观察小旗在旋转过程中什么变了、什么没有变。经过观察、思考和小组交流,学生不难发现,旋转后的小旗(不考虑小棒)会形成一个圆锥体,小旗的一条直角边(小棒所在的边,不是小棒全长)不变,是圆锥的高,小旗的另一条直角边变成了圆锥的底面半径。也就是说,硬纸板绕一条直角边旋转一周会分别形成底面半径8 厘米、高6 厘米以及底面半径6 厘米,高8 厘米的圆锥。学生能这样描述图形的运动变化,就能很快用公式分别求出它们的体积是π×6×6×8÷3=96π 立方厘米、π×8×8×6÷3=128π 立方厘米。
教师引导学生借助已有表象描述物体的运动和变化过程是帮助他们形成空间观念的重要环节。学生通过有效操作,在大脑中逐渐形成三维映像,实现二维平面图形的三维视觉化,他们对图形的运动形成初步映像后再用数学语言进行描述,就能实现对数学问题的结构性理解,就能从中发现一些解决问题的有用信息,就能在解决问题的过程中充分感悟描述图形的运动变化过程对自己发现解题思路、形成空间观念的独特作用。
三、画图表示信息
学生依据信息画几何图形也是空间观念的重要表现形式之一。画几何图形主要包括画常见平面图形以及彼此之间的关系图、画简单图形的位置、运动与变化情况等。根据相关信息画图是学生的思维与外部语言、操作技能协同作用的结果,是学生借助表象和已有经验进行“数学地思考”的过程。虽然数学课程标准没有要求小学生画立体图形,但如果他们能根据题目中的信息画出相应的示意图,就会对顺利解决问题产生很大的促进作用。
如教学“长方体和正方体”时,学生常常会遇到这样的一道习题:如果把一个长方体的高增加2 厘米,它就会变成一个正方体,并且正方体的表面积会比原来增加56 平方厘米。你能求出这个长方体的体积吗?如果凭空想象,学生解决问题就会比较困难。如果学生能根据习题所描述的数学信息正确画出示意图,就能化难为简,就能迅速、正确地解决问题。学生可以先画一个长方体,然后把高增加2 厘米,变成正方体(如图2)进行观察(也可以先画出一个正方体,然后把高减少2 厘米,得到原来的长方体)。学生从图中不难发现,长方体变成正方体,高增加2 厘米,表面积增加部分就是虚线表示的前、后、左、右4 个小长方形面积,56 平方厘米就是4 个相同小长方形的面积之和,从而求出小长方形的长(即正方体的棱长)是56÷4÷2=7 厘米,长方体的体积是7×7×(7-2)=245 立方厘米。
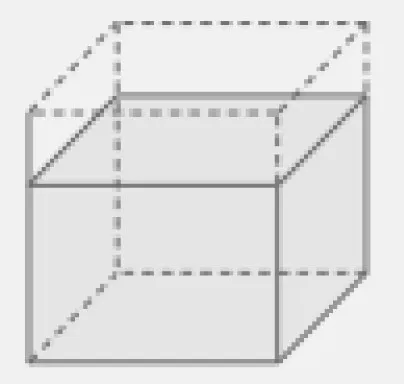
图2
画图表示数学信息不但能帮助学生正确理解题意,而且能帮助学生整体把握问题、迅速发现问题解决的思路。[4]教师引导学生尝试画图,使学生在掌握长方体表面积、体积和长方形面积知识的基础上,正确理解表面积增加的含义,为顺利解决问题奠定了坚实的基础。学生通过画图把表面积增加的表象视觉化,使几何事实得到真实再现。学生的空间观念就会在实物几何化中逐渐得到发展。
总之,想象能帮助学生建立物体表象,描述是对数学信息的客观叙述,画图是对数学信息的直观展示。想象、描述和画图是培养学生空间观念的渐进途径。明确这些途径,教师培养和发展小学生的空间观念就会事半功倍。
