基于PCA-PSO-BP神经网络的管道剩余强度评价

中国石油新疆油田公司风城油田作业区

截至目前，我国部分油气管道已连续运行超过10 年，经过长时间的腐蚀，管道内不可避免地会出现各种缺陷，缺陷的存在会引起穿孔事故，从而引起油气资源泄漏，同时，也会使得油气管道的剩余强度下降[1-2]。国内外专家提出了诸多管道腐蚀速率研究成果，证明该方面的研究较为深入，在缺陷管道剩余强度方面，尽管提出了诸多计算方法，但这些方法的计算过于保守，虽然有利于管道安全，但是也会导致管道输送效率严重下降问题。因此，如何对缺陷管道的剩余强度进行准确计算和预测成为了研究重点。

目前，国内外学者对单缺陷管道的剩余强度问题展开了全面研究。英国学者JONES 等[3]根据可靠性理论，提出了一种计算管道剩余强度的方法，但是该方法需要考虑的因素较多，使用过程较为繁琐，因此并没有得到大面积的推广和应用；加拿大学者ORISAMOLU 等[4]根据管道剩余强度计算的半经验公式B 31G准则和概率方法，提出了管道剩余强度计算的新模型，由于该模型并没有考虑缺陷外形对缺陷剩余强度的影响，因此，其计算误差相对较大；WANG 等[5]采用有限元法得到了适用于油气管道剩余强度评价的计算方法，但是该方法并没有在所有钢级材料中得到验证，且有限元分析法的使用过程较为繁琐，不利于现场工程人员使用；顾晓婷等[6]分析了流变应力与膨胀系数对常见的剩余强度评价方法评价结果的影响，并使用这些方法对不同钢级的管道进行了适应性分析，但是适应性分析的管道中并没有高强度管道。

通过以上分析可以发现，对于管道剩余强度评价方法，尽管已经出现了大量的研究成果，但是都存在一定的缺陷。在人工智能快速发展的大背景下，如何应用智能算法进行管道剩余强度预测是一个难点问题。针对此问题，本次研究提出了一种改善管道剩余强度预测结果的人工智能方法。该方法将从影响管道剩余强度的因素出发，应用PCAPSO-BP 神经网络模型对单缺陷管道剩余强度进行预测，并将预测结果与常见评价方法进行误差对比，以此研究该模型的可行性。

1 管道剩余强度影响因素分析

对管道剩余强度产生影响的因素可以分为两类，一类是管道自身因素，包括管道的钢级、直径、壁厚、屈服强度及拉伸强度等；另一类是管道缺陷因素，包括缺陷的类型、长度、宽度以及深度等[7]。

不管是缺陷管道还是完整管道，管道自身因素都会对其剩余强度产生重要影响。首先，从理论上讲，随着管道钢级的升高，其剩余强度逐渐增大；随着管道直径的增大，其剩余强度逐渐降低；随着管道壁厚的增加，其剩余强度逐渐增大[8]。屈服强度和拉伸强度都会对管道的剩余强度产生间接影响，随着屈服强度和拉伸强度的逐渐增加，管道的流变应力逐渐增加，其剩余强度也会逐渐增加。

管道的缺陷因素是影响缺陷管道剩余强度的主要因素，目前国内外专家对缺陷长度、宽度、深度与剩余强度之间的关系展开了深入研究，取得了一定的成果。研究成果表明，随着缺陷长度的逐渐增加，管道的剩余强度逐渐降低，但是，当长度增加到一定数值以后，其剩余强度将逐渐趋于定值[9]；随着缺陷宽度的逐渐增加，其剩余强度也会逐渐降低，但是缺陷宽度对剩余强度的影响较小，可以忽略不计，因此，在本次研究中将忽略该因素的影响；随着缺陷深度的逐渐增加，其剩余强度逐渐降低。缺陷类型主要可以分为四种，分别是矩形缺陷、椭圆形缺陷、槽型缺陷以及不规则形状缺陷，缺陷类型是否会对剩余强度产生影响尚不明确[10]。

通过以上分析，在本次研究中将首选管道的钢级、直径、壁厚、屈服强度及拉伸强度、缺陷长度、缺陷深度以及缺陷类型八种影响因素作为管道剩余强度预测的影响因素。

2 数据来源及模型搭建

2.1 数据来源

为了确保本次研究成果的准确性，预测过程数据将采用实际爆破数据。ASME、挪威船级社等协会在总结管道剩余强度公式时进行了管道爆破，并将数据进行了公布，因此，本次研究将采用诸多协会的管道爆破数据，数据从文献[11]～[19]中获取，总共收集到148 组，这些数据包含X35～X100 内的所有常见钢级类型。将其分为两个类别，随机选取128组数据作为学习数据，剩余20组数据作为预测数据，学习数据和预测数据中都包含所有钢级类型，确保本次研究的科学性和可靠性。

2.2 PCA算法

PCA（主成分分析）算法是常见的数据降维方法，一般来说，研究过程所考虑的管道剩余强度影响因素越多，其预测结果越准确，但是研究过程越复杂。在另一方面，某些影响因素之间存在互相关联的关系，在研究中可以忽略某些因素的影响，而PCA 算法正是排除关联影响因素的有效方法[20]。PCA算法通过分析各影响因素对剩余强度的贡献率及累计贡献率，得到影响管道剩余强度的主要因素，仅考虑主要因素即可对剩余强度进行准确预测。

首先将剩余强度影响因素组成为矩阵X，然后依次计算该矩阵的相关系数矩阵R、相关系数的特征值λi、相应的特征向量αi，以及影响因素的累计贡献率，相关性系数矩阵R、主成分贡献率及累计贡献率的计算公式为

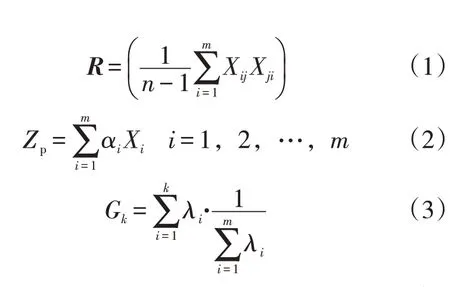
式中：R表示相关系数矩阵；Xij表示矩阵X第i行第j列的数据；αi表示特征向量；Xi表示矩阵X的第i行数据；Zp表示计算得到的主成分贡献率；Gk表示前k项数据的累计贡献率。

通常状况下，当前k项影响数据的累计贡献率大于80%时，即可使用这些影响因素进行预测研究。但是，在本次研究中，为了保证预测结果的科学性和准确性，将累计贡献率大于98%的前k项腐蚀速率影响因素代替所有影响因素输入到PSO-BP神经网络模型中进行学习预测。

2.3 PSO-BP神经网络算法

BP 神经网络是最常见的分类及预测算法之一，其自身含有三层网络结构，分别是输入层、隐含层和输出层，其网络结构如图1所示。

图1 BP神经网络结构Fig.1 BP neural network structure

在图1 中，x1，x2，…，xn表示输入变量，y表示输出变量，W1j，W2j，…，Wnj表示输入层与隐含层之间的权值，bj表示隐含层内的阈值，Wj1表示隐含层与输出层之间的权值，φ、ψ表示激励函数。

在数据信号传播过程中，隐含层内第j个节点处的输入值为

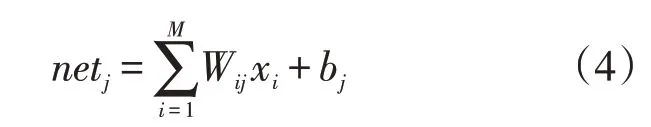
隐含层内第j个节点处的输出值为

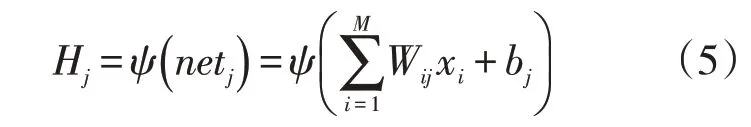
输出层内的输入值为

输出层内的输出值为

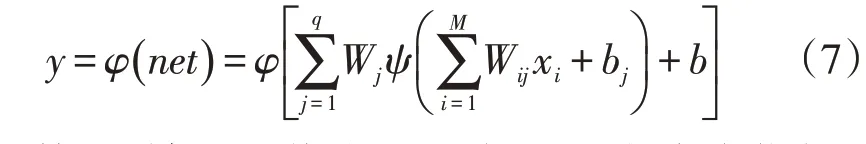
尽管BP 神经网络在预测方面具有诸多优势，但是其权值和阈值的选择是一项关键问题，当选择不当时，容易造成神经网络陷入局部极小的问题出现，从而导致预测误差较大。因此，在本次研究中引入了PSO（粒子群）算法对权值和阈值进行寻优[21]。PSO 算法是根据鸟群的捕食行为进化而来的一种算法，其本质就是通过个体间的合作与信息共享行为来寻找目标参数的最优解。

在本次研究中，应用PSO-BP 神经网络算法的流程如图2 所示。首先将BP 神经网络算法中的权值和阈值作为PSO算法中的粒子及速度，然后使粒子在空间内运动，不断更新每个粒子的位置和粒子群体的位置，在所有可能达到的位置处寻找最佳位置，从而得到权值和阈值的最优解；然后将相关数据输入到BP神经网络模型中进行学习和预测。

将本次研究收集的148组管道剩余强度及相关影响因素数据分为两类，其中128组数据作为模型的训练样本，剩余的20 组数据作为模型的预测样本，使用128组数据对模型进行训练，对20组数据进行预测，将预测得到的管道剩余强度数据和实际的剩余强度数据进行对比，以此验证本次研究所提方法的可行性。

图2 PSO-BP神经网络算法流程Fig.2 Flow chart of PSO-BP neural network algorithm

3 预测结果分析

3.1 PCA处理结果

在本次研究中，首先使用MATLAB软件对数据进行PCA 降维处理，由于MATLAB 中不能输入非数字数据，因此，需要对某些参数进行转换。首先，对于管道类型而言，由于钢级仅是管道的代号，并无实际意义，因此可以将管道钢级前的字母去除，即将X80 转换为80，X100 转换为100；其次，对于管道缺陷类型，将矩形缺陷定义为1，椭圆形缺陷定义为2，槽型缺陷定义为3，不规则形状缺陷定义为4；最后将数据输入至PCA算法中进行贡献率分析。分析结果如表1所示，从表中可以看出，管道钢级是影响管道剩余强度的主要因素，同时，屈服强度和拉伸强度对剩余强度的贡献率较低，可以忽略不计，从侧面分析，这主要是因为管道钢级与屈服强度和拉伸强度具有一定的关联性。为了保证预测结果的准确性，此次研究将选用累计贡献率超过98%的因素作为管道剩余强度的影响因素。因此，本次将选用管道钢级、直径、壁厚、缺陷类型、长度、深度作为管道剩余强度的影响因素进行下一步研究。

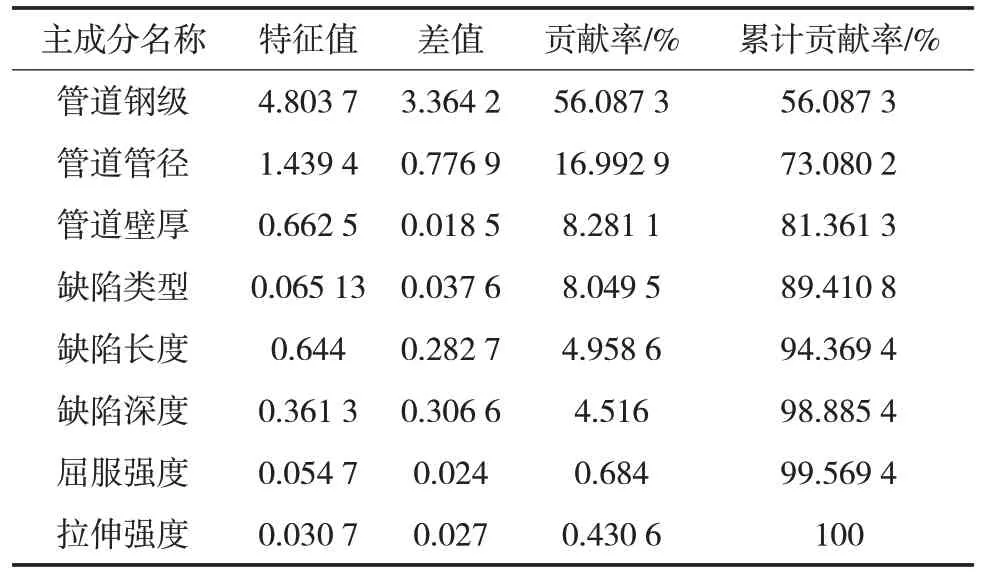
表1 PCA降维结果Tab.1 PCA dimensionality reduction results

3.2 PCA-PSO-BP神经网络模型预测结果

根据PCA 算法的处理结果，将管道钢级、直径、壁厚，以及缺陷类型、长度、深度作为管道剩余强度的影响因素，在MATLAB中建立PSO-BP神经网络模型，使用128 组数据作为模型的训练样本，剩余20 组数据作为模型的预测样本，对单缺陷管道的剩余强度进行预测，将预测结果与实际剩余强度、ASME B31G—2009 计算结果、DNV RPF101 计算结果、API 579 计算结果、SYT6151—2009 计算结果进行对比，ASME B31G—2009、DNV RP-F101、API 579、SYT6151—2009 四种方法的计算如公式（8）～（16）所示。计算各种方法的平均绝对误差和均方根误差，每种方法的计算结果、计算误差如图3、图4 及表2 所示。从图表中可以看出，PCA-PSO-BP神经网络模型预测结果的最大误差不超过10%，平均绝对误差仅为2.923%，均方根误差仅为0.535 875 231，最大误差、平均绝对误差以及均方根误差均小于其他管道剩余强度计算方法，证明该种方法可用于管道剩余强度预测。

（1）ASME B31G—2009方法

（2）DNV RP-F101方法

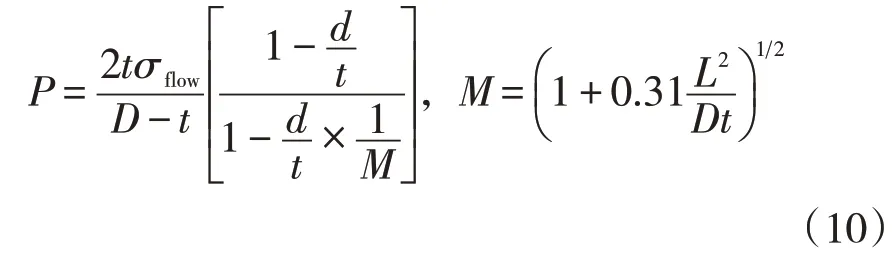
（3）SYT6151—2009方法

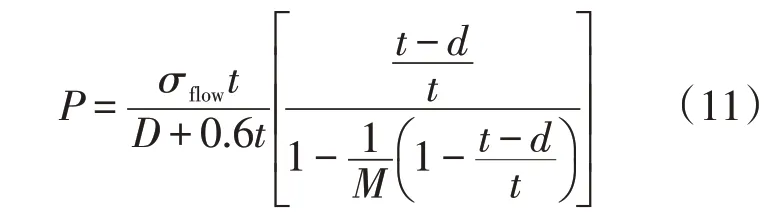
M=1.001-0.014 195λ+0.290 90λ2-0.096 420λ3+0.020 890λ4-0.003 054λ5+2.957×10-4λ6-1.846 2×10-5λ7+7.155 3×10-7λ8-1.563 1×10-8λ9+1.465 6×10-10λ10

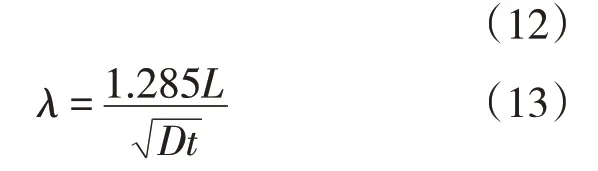
如果λ＞20，则λ取20。

（4）API 579方法

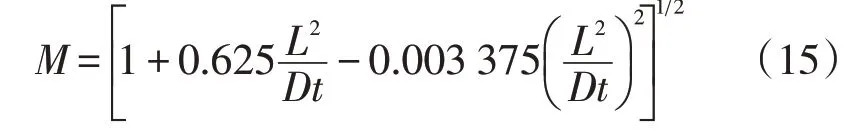
式中：M为管道的膨胀系数；t为管道的理论壁厚，mm；σflow为管道的流变应力，MPa；D为管道外径，mm；σs为管道屈服强度（可用SMYS 表示，SMTS 表示拉伸强度），MPa；P为管道的剩余强度，MPa；d为管道缺陷的最大深度，mm；L为管道缺陷长度，mm。

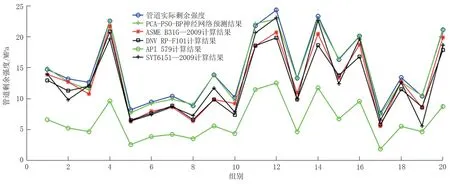
图3 管道剩余强度预测结果Fig.3 Prediction results of pipeline residual strength

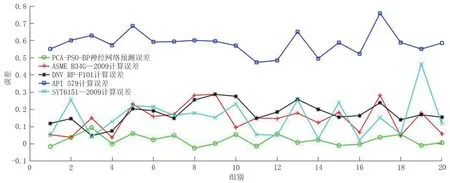
图4 预测结果误差Fig.4 Prediction result error

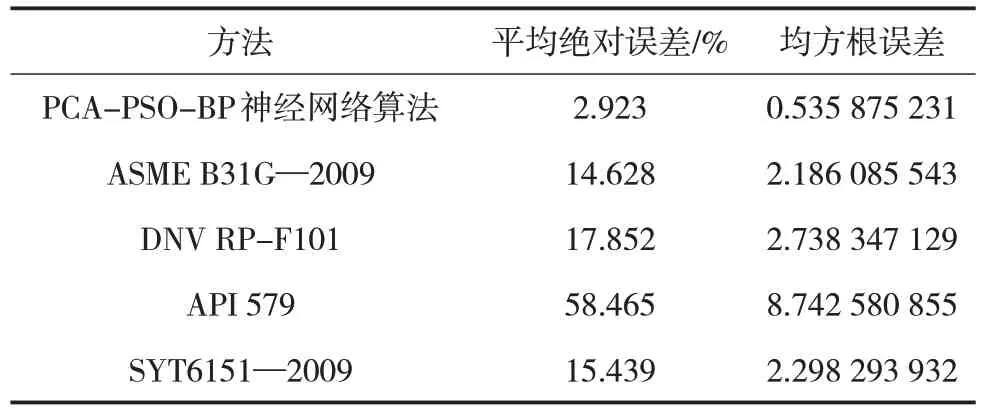
表2 不同方法计算结果平均绝对误差及均方根误差Tab.2 Average absolute error and root mean square error of different methods

4 结论

在本次研究中，首先对影响单缺陷管道剩余强度的相关因素进行了分析，通过建立PCA 模型对影响因素进行了降维处理，根据降维结果随机选取128 组数据作为PSO-BP 神经网络模型的学习样本，剩余20 组数据作为模型的预测样本，对管道剩余强度进行了预测，并将预测结果与其他常用计算方法进行了误差对比，由此得出以下结论：

（1）在管道剩余强度的影响因素中，管道钢级对管道剩余强度的影响最大，而屈服强度和拉伸强度对管道剩余强度的影响最小，从侧面证明管道钢级与屈服强度和拉伸强度存在着一定的关联。由于管道钢级、直径、壁厚、缺陷类型、缺陷长度、缺陷深度对管道剩余强度的累计贡献率超过了98%，因此可选用这6种影响因素作为管道剩余强度的主要影响因素进行研究。

（2）通过使用PCA-PSO-BP神经网络模型对管道剩余强度进行实际预测后发现，该模型的预测结果的最大误差不超过10%，平均绝对误差仅为2.923%，均方根误差仅为0.535 875 231，三项数据都远小于其他方法的计算结果，证明该方法可用于管道剩余强度预测。

5 展望

基于PCA-PSO-BP神经网络模型的管道剩余强度预测方法，尽管应用该方法的预测精度相对较高，但是仍然存在应用不方便的问题，因此，还需要进行以下两方面的研究：

（1）通过使用各种类型的编程软件，使得基于人工智能的管道剩余强度预测方法可以形成可视化的软件，能够使油田现场工作人员的使用更加方便。

（2）本次研究所提出的方法只是使管道剩余强度预测结果的准确度得到了提升，但是管道剩余寿命才是油田单位最为关注的问题，因此，相关研究人员需要在对剩余强度进行研究的基础上，提出改善管道剩余寿命预测结果的方法。