基于三维地形的气田星枝状管网路径优化研究*

任魁杰 孙笼笼 万涛 韩斌 孟良 姚林 侯磊

1中国石油化工股份有限公司华东油气分公司

2中国石油大学（北京）机械与储运工程学院

气田集输系统呈多级网络结构，建造费用高，通常占整个地面工程投资的60%～70%。以往优化设计计算过程中大多忽略地形起伏，优化结果与工>程实际相差较大[1]。20 世纪60 年代初，Kuhn-Tucker定理被应用于管网优化设计领域，求解管道系统在非线性约束条件下的最优解。1979 年，BHASKARAN等将天然气集输管网优化分解为管径分派、站点选择和管网布局等3个子问题，并用线性规划法求解[2]。2005年，魏立新等将优化问题分解为管网布局优化和参数优化[3]。考虑地形的管网优化研究出现较晚，2013 年，冉明鑫对煤层气星树状集输系统进行优化研究，在布局优化中考虑了地形因素对管线走向和站址选取的影响[4]。2014年，张思琦等研究了煤层气集输系统中的三维选线和滚动开发问题，以管道长度最短为目标函数，采用遗传算法进行求解，实现了煤层气集输系统的三维路径优化[5]。早期的管网优化研究考虑地形因素较少，研究重点多集中于二维布局优化、参数优化以及优化问题的求解上。关于三维路径的研究多集中于单条管线的路径规划上，而将管线曲面路径直接融入进优化模型的研究较少，管网优化和地形处理多被孤立对待。本文针对星枝状管网拓扑结构，采用蚁群算法计算三维地形中各节点之间的曲面最短距离，并基于曲面最短距离将管网优化分为井组划分、干支管网连接、中心处理站站址3个子问题分别求解，实现了三维地形管网路径优化。

1 曲面最短路径求解

1.1 三维地形的建立与处理

应用真实地形有限高程点数据，通过四格点样条函数内插法构建气田所在区域的真实地形，然后对三维曲面进行网格划分。分别沿水平方向和纵向将三维曲面按照一定间距分割，水平间距和纵向间距可以动态调整，得到若干新曲面，网格线的交点即为可选择的路径点[6]。曲面划分完成后，将曲面上的全部路径点按照“从下至上、从左至右”的顺序依次编号，用于储存路径信息。如图1所示，左下角为起始点，编号为1，x轴方向为n-1 等分，y轴方向为m-1 等分，右上角位编号的终点记为nm。

1.2 三维地形路径规划求解方法

蚁群算法是模拟蚂蚁觅食原理用来在图中寻找优化路径的机率型算法[7]。路径越短，路径上经过的蚂蚁越多，遗留的信息素也越多，信息素浓度也越高，由此构成正反馈过程，从而逐渐地逼近最优路径。在用蚁群算法求解三维曲面上两点之间的最短路径时，算法的性能受很多参数的影响，其主要影响参数包括种群规模、初始信息素、信息素挥发系数、信息素启发因子、期望值启发因子和状态转移概率。参数的确定需要根据计算结果动态调整。

图1 曲面路径点编号示意图Fig.1 Schematic diagram of path point namber in curved surface

1.2.1 种群规模

蚁群的规模影响算法的搜索能力。蚂蚁数量较多时，算法的全局搜索能力强，稳定性高，但是数量过多会使算法的随机性增加，收敛缓慢；蚂蚁数量少时，算法稳定性低，全局搜索能力弱。可根据现场给定的气井数量，对比不同数量时的优化距离和计算时间，确定种群规模。

1.2.2 初始信息素

初始信息素储存在路径节点上，影响蚁群算法的寻优速度。为了加快算法收敛速度，初始信息素设置为

式中：τ0(i,j)为路径节点(i,j)的初始信息素含量；S1为路径节点与起始点间的距离；S2为路径节点与终点间的距离。

1.2.3 信息素挥发系数

信息素挥发系数的取值影响蚁群算法的收敛速度和全局搜索能力。挥发系数较大时，被搜索过的路径点上信息素衰减快，存在时间短，蚂蚁再次搜索该节点的概率较低，导致算法的正反馈作用减弱，随机性增强，收敛速度减小，求解质量降低；挥发系数较小时，信息素的正反馈作用增强，算法随机性减弱，收敛速度快，但易陷入局部最优。信息素挥发系数的取值在0.1～0.5之间效果较好。

1.2.4 信息素浓度更新

在蚁群算法中，路径上的信息素浓度会随着时间的推进而逐渐衰减。在迭代计算过程中路径上的信息素浓度需进行实时更新，信息素更新模型采用公式（2）蚁周模型，按照公式（3）和（4）更新信息素矩阵[8]。

1.2.5 信息素启发因子

信息素启发因子α用来衡量信息素作用的大小。α值越大，蚂蚁选择之前走过的路径可能性就越大，算法的随机性减弱，当α取值过大时，算法易陷入局部最优；当α取值较小时，算法的随机性增强，收敛速度减慢。

1.2.6 期望值启发因子

期望值启发因子β反映了蚁群在道路搜素中的先验性、确定性等因素的强弱。β取值越大，蚂蚁个体选择距离较近节点的概率越大，算法随机性减弱，易陷入局部最优；β取值越小，算法随机性越强，取值过小时，算法无法找到最优解。节点i转移至j的期望函数为公式（5），表示蚂蚁从i节点转移到j节点的概率。

式中：ηij为节点i转移至节点j的期望值；[x(i,j)，y(i,j)，z(i,j)]为转移点处的坐标；[xend，yend，zend]为终点坐标。

1.2.7 状态转移概率

状态转移概率是蚂蚁能够在节点间完成搜索的决定性因素。每个网格点周围有8个相邻点，通过计算各点的转移概率确定下一步的路径点，状态转移概率计算公式为

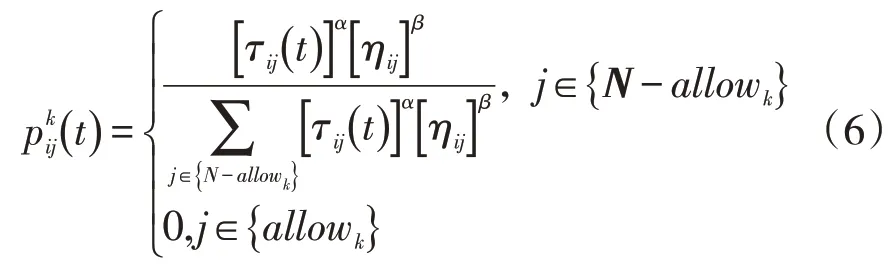
2 三维管网布局优化

站场集气流程采用集气站和中心处理站两级布站，管网拓扑结构采用星枝状，井口产物经星状管线进入各井组集气站，在集气站处理后通过枝状管网输送到中心处理站。管网优化分为井组划分、干支管网连接、中心处理站站址3 个子问题，通过K-medoids 中心点聚类法进行井组划分并确定各井组集气站站址。确定集气站站址后，通过Prim 算法求解支干管线布局的最小生成树。最后通过弗洛伊德算法确定中心处理站站址，完成最终优化。

2.1 井组划分

把单个数据对象的集合划分为类似样本组成的多个簇或多个类的过程叫聚类[9]，井组划分问题可归于聚类问题，基于划分的聚类算法就是用统计分析的方法研究分类问题。常用的基于划分的聚类分析方法有K-means 聚类法和K-medoids 中心点聚类。K-means聚类法在样本数据中出现了不合理的极端值时，会导致最终聚类结果产生一定的误差，而K-medoids中心点聚类法有很强的鲁棒性，在削弱异常值和离群点的影响上效果显著。因此采用K-medoids 中心点聚类法进行井组划分[10]，其计算步骤如图2所示。

井组划分完成后，最终的聚类中心即为相应井组的集气站。K-medoids 中心点聚类法用于井组划分的约束条件主要包括隶属关系约束、集气半径约束、井式约束和处理量约束。

（1）隶属关系约束，即每口井只能连接到1座集气站，而1座集气站可以连接多口井。

式中：K为集气站数；i表示集气站的序号；Aij为管段决策变量，取0或1。

（2）集气半径约束，即井口到集气站的距离不能超过最大限度。

式中：Ri为第i口井的集输半径，km；Rmax表示允许的最大集输半径，km。

图2 K-medoids中心点聚类法井组划分流程Fig.2 Well group division process of K-medoids central point clustering method

（3）井式约束，即1座集气站汇集的井口数量在一定范围之内。

她丈夫从小跟着父亲在这店铺里学手艺，学成后就接手这店铺，一直做到现在。“早些年村里人多，一天到晚忙不过来，喝口茶的工夫也没有，现在村里人少了，一天挣不了几个钱。”

式中：Nmin为集气站允许汇集的井口数量下限；Nmax为集气站允许汇集的井口数量上限。

（4）处理量约束，即集气站的处理量在一定范围之内，保证产气量的均衡分配。

式中：Qmin为集气站气体处理量的最小值，m3/d；Qmax为集气站气体处理量的最大值，m3/d；qi为第i口井的产量。

2.2 支干管网连接优化

支干管网连接以管线长度作为管线权值，在确定集气站的选址之后，需要对支干管网进行优化，支干管网的优化必须满足其连接方式的合理性，尽可能减少管线的用量。为了得到各个站场的连接方式，采用几何拓扑学中无向枝状结构的连接方法构建管网路径，无向网络图表达式如下：

式中：G为无向网络图；V为站点数；E为管段线集。

无向网络图是将节点通过边连接而成的路径图。以管线长度最短为原则，建立无向网络图的最小生成树数学模型，模型求解采用Prim算法[11]，代入决策变量则有

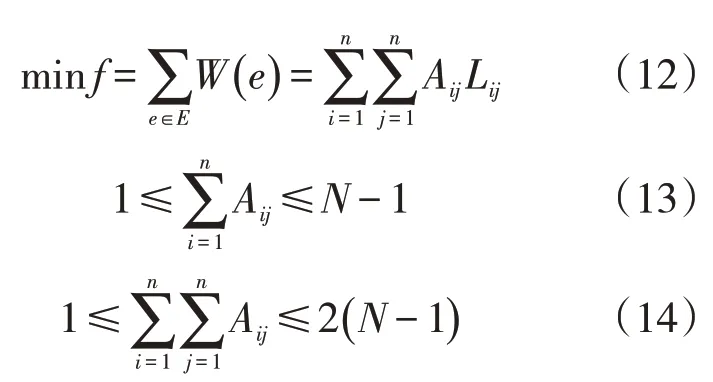
式中：N为管段数量；Lij为i节点到j节点的管线长度，m；Aij为管段决策变量，取0或1。

2.3 中心处理站站址确定

经过支干线连接优化，管网布局基本确定。但是实际工程中，管网中天然气的流动是具有一定方向的，需要选择中心站点，从而确定管网中流体的流向和管径。中心站点的选取原则是以所有站点到某一点的流量长度之和最短所对应的点即为中心站。

式中：Wn为所有站点到某一点的流量长度之和中的最小值，m3/d；n为井组中的井口数；i为集气站第i口井；j为第j口井；qj为第j口井的流量，m3/d；Lij为第i口井到第j口井的距离，m；N为管段数量。

3 算例分析

以某地形起伏区域气田为例，建立三维地形模型，模型东西长2.8 km，南北长1.8 km，最大高程差197 m，在该区域有41 口井，井位如图3 所示。气井采用自压采气，假设各井口产气产液量相同，且产气量为4×104m3/d，产液量为15 m3/d。

图3 三维地形与井口分布Fig.3 3D terrain and wellhead distribution

根据以上优化模型以及图3所示的三维地形及井口分布进行管网路径优化，将优化后的管线路径绘制在三维地形中，如图4所示。采气管线总长度为38.237 km，支干线总长度为8.677 km。

为对比三维管网路径优化结果，将管网路径优化中的两点之间三维曲面最短距离改为传统的二维平面距离，即将三维优化改为传统的二维优化，其他优化方法和原则保持不变，优化后的二维平面优化结果如图5所示。

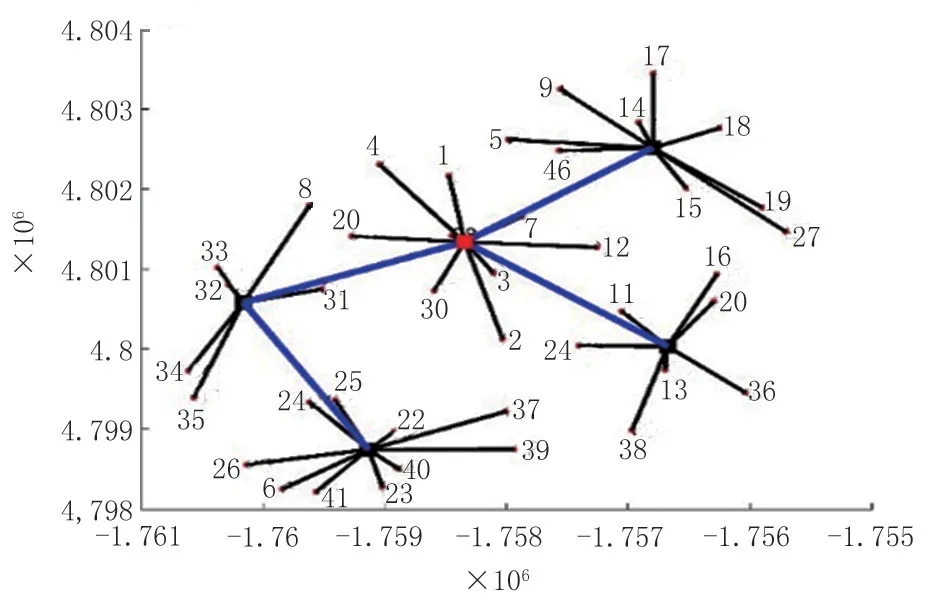
图5 二维管网优化结果Fig.5 Two-dimensional pipe network optimization results

图6 二维管网优化管线路径Fig.6 Two-dimensional pipeline network optimization pipeline path

根据二维平面优化后节点间的连接关系，采用蚁群算法计算具有连接关系的两点之间曲面最短路径，并绘制三维管网路径图，如图6所示。根据计算结果，三维地形中采气管线实际路径总长度为42.407 km，三维地形中支干线实际路径总长度为12.370 km。由此可知，三维布局优化管线总长度为46.914 km，二维布局优化管线总长度为54.777 km，三维优化相比于二维优化，管线长度降低14.35%。

4 结论

应用真实地形有限高程点数据，通过四格点样条函数内插法构建真实地形，并对地形进行网格划分，采用蚁群算法和轮盘赌算法完成了曲面两点之间最短路径的求取。根据两点之间曲面最短距离，针对井组划分、干支管网连接、中心处理站站址优化建立了三维地形管网分级优化模型。实际算例结果表明，与二维平面优化对比，三维管网优化能够显著降低管网总长度和管线投资。