浅海中非金属圆柱体的扰动电场

喻 鹏，程锦房，姜润翔

(1. 海军工程大学 兵器工程学院， 湖北 武汉 430033； 2 . 海军工程大学 电气工程学院， 湖北 武汉 430033)

在“9·11”事件之后，港口防御越来越受到各国重视，针对水下慢速移动小目标(如UUV、ROV、蛙人等)的探测，目前主要采用声呐技术[1]。但是在港口等浅海条件下，高环境噪声和强混响等使得声呐探测存在较多缺点[2-3]，为此亟须研究其他探测方法作为声探测的补充[4]。

受弱电鱼和海洋可控源电磁勘探方法的启发，有学者提出采用主动电场探测的方法作为浅海环境下声探测的补充。主动电场探测方法具有受海洋环境影响小、对金属和非金属物体均具有较好的探测效果的特点。美国最早于20世纪70年代进行了主动交流电场探测蛙人的实验，其主要采用1对发射电极和2对测量电极，受限于当时传感器等设备的精度，仅能探测测量电极附近2 m范围内的蛙人[5]，之后未见过相关报道。

国内在主动电场探测领域的研究在近几年才展开，主要是基于弱电鱼的捕食机理，对近距离的目标进行定位，如：文献[6]重点研究了铁、铜、铝等金属材料在1～1000 Hz交变电场作用下的感应电势，建立了主动电场定位系统的等效电路模型；文献[7-8]研究了金属和非金属材料在不同频率电场作用下的定位曲线，主要应用于超短距离情况下定位水下管道缺陷的位置、导航等。可以看出，上述文献重点关注近距离范围内(距离小于20 cm)对目标的定位，而较少研究利用主动电场法进行较大范围内目标的探测、跟踪。

国外除了对弱电鱼的电场探测机理展开研究外，还借鉴大地电磁勘探法原理(与弱电鱼电场探测具有相似性)研究了在较大区域范围内对目标的探测，如：文献[9]采用拖曳电极阵列，对海水中电导率不一致的目标进行探测；文献[10-11]提出采用直流电阻率异常的方法，利用固定电极线阵对水下非金属目标进行探测，并利用缩比模型初步验证了所提方法的可行性；之后文献[12]在文献[11]的基础上采用双极方波作为激励源，通过测量电极线阵上的电位变化，实现对目标的实时探测定位，并利用缩比模型实验和海试验证了方法的可行性。

文献[10-12]重点研究了缩比模型条件下主动电场探测非金属物体的可行性，而未对主动电场作用下目标周围的扰动电场分布特性进行理论建模。事实上，对金属目标的二次偶极子模型的研究较多，但是对表面电阻率远大于海水电阻率的非金属目标的二次偶极子模型研究都很少。所以本文基于镜像法和网格化思想建立了非金属圆柱体目标在主动电场作用下所产生的二次电偶极子模型，即扰动电场模型。为了验证所建立模型的正确性，文中首先与边界元软件的仿真结果进行了对比，结果表明所建立模型的计算结果与边界元软件的仿真结果具有较高的相似性；最后在水池进行了模型实验，实测结果与文中模型计算值基本一致，进一步说明所建立模型的正确性。

1 模型建立

主动电场探测的基本原理为：通过一对发射电极(一般为石墨电极、钛电极等不易电解、电阻率低的材料)向均匀电导率介质中发射电流，建立初始电场(文中定义为一次场)；当有外来目标进入介质时，由于外来目标的电导率与周围介质的电导率不一致，目标将与原环境场相互作用，在目标位置处诱导第二偶极子，第二偶极子在特定测点上的电场扰动是目标位置、大小、形状和电阻率对比度的函数，文中定义这个扰动场为二次场。一般通过Ag/AgCl电极或者碳纤维电极等获取特定测点上的电场扰动值，经信号处理、分析实现对目标的探测、跟踪以及定位。实际使用中，为减小电极等材料极化效应的影响，一般采用低频双极性方波、正弦波等代替，但是由于信号频率很低，文中理论分析时将发射信号源作为直流进行处理。

1.1 一次场模型

建立如图1所示的三层模型下主动电场探测，其中一对发射电极平行布放在海水中，电极深度为d，测量电极布放位置靠近海床，海水深度为h，空气、海水、海床、目标的电导率分别为σ0、σ1、σ2、σt，其中σ0=0。

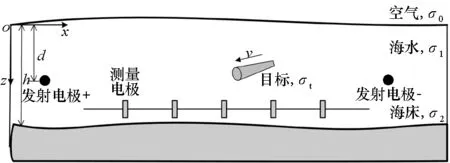
图1 主动电场探测示意Fig.1 Diagram of active electric field detection

采用文献[13]中的镜像法，对图1中的电场分布进行建模。根据图1中的坐标系，设两个发射电极的坐标为(x0,0,d)和(x1,0,d)，目标中心的坐标为(xt,yt,zt)，由于两个发射电极的电流大小相等、方向相反，所以计算时可先计算单个发射电极在测量点位置产生的电场值，之后对两个发射电极产生的电场求矢量和。

单个发射电极在目标所在位置处产生的电位值如式(1)所示[14-15]，其中I为发射电流。对于式(1)，实际计算时取n=10即可达到较高的精度[16]。

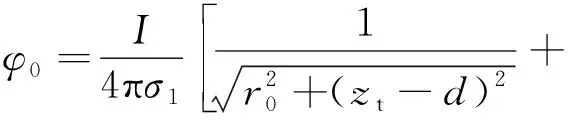
(1)

式中：

(2)

(3)

之后根据式(4)即可求得目标位置处不同方向的电场分量Ex、Ey、Ez，式中r即代表x、y、z方向。三分量电场Ex、Ey、Ez的具体表达式可参考文献[13]。

(4)

1.2 二次场模型

当目标出现时，在目标位置处会诱导第二偶极子，第二偶极子在特定测点上的电场扰动(即二次场)是目标位置、大小、形状和电阻率对比度的函数。目标的形状各异，所以一般将目标等效为球体，利用式(5)进行估计，其中a为目标的等效半径，rt为以目标中心为原点、待求区域的位置矢量，E0为环境电场，u(rt)为电位扰动值[14-15]。

(5)

然而实际环境中，目标不可能为标准球体，更多的是以类似圆柱体的形式出现，那么将目标等效为球体的方式会引起较大的误差，而且等效半径较难确定，所以将目标等效于圆柱体是合适的。

为了对非金属圆柱体目标产生的扰动电场进行建模，本文提出一种网格化的电偶极子等效法，该方法限定于：①激励源为直流源；②非金属目标表面电阻率是均匀的，且远大于海水电阻率。为方便计算，假设圆柱体目标轴线平行于y轴，目标中心坐标为(xt，0，zt)。

当圆柱体目标出现时(圆柱底部半径为R，长度为L)，目标位置处的电流方向会发生改变，电流会绕过圆柱体由其上方和下方流向负极。由于沿y轴方向的电流密度存在差异，那么可沿y轴方向将圆柱体目标分成m个长度为L/m的圆柱单元，每个圆柱单元定义为偶极子Di(i=1,2,…,m)，其中心坐标为(xt,yti,zt)。m的确定原则是保证每个圆柱单元沿y轴方向的电流密度基本一致。目标划分示意如图2所示。

图2 圆柱体目标等效为m个偶极子Fig.2 Cylindrical object is equivalent to m dipoles

首先求出偶极子Di的电偶极矩Pi，再根据1.1节的一次场模型即可求出目标位置处的电场分量Ex、Ey、Ez。

假设偶极子Di位置处的初始电场分量为Exi，根据式(6)即可求得目标位置处的电流分量jxi：

jxi=σ1Exi

(6)

那么偶极子Di的等效电流值Ii可由式(7)计算，其中ΔS为每个圆柱单元沿x轴方向的半投影面积，ΔS=RL/m。

Ii=jxiΔS

(7)

偶极子Di的等效水平电偶极矩Pi为：

Pi=IiR

(8)

那么测量点处的电场Etotal为各个电偶极子Di在测量点产生电场的矢量求和：

(9)

式中，Q(·)代表根据1.1节的方法进行水平分量电场求解计算，其中zp为待求解平面的坐标。值得注意的是，当待求解平面位于目标下方时，由于目标为绝缘体，沿x轴方向流经目标的电流会向待求解平面平移R距离，那么在计算目标下方的扰动电场时需要将等效电偶极子的纵坐标向下移动R距离。

2 仿真实验验证

2.1 实验条件

采用边界元软件建立了三层介质模型，主要参数如下：定义坐标系中z为垂直向下方向，海面位置z=0 m，z<0为空气层，0≤z≤60 m为海水层，z>60 m为海床；一对发射电极之间距离100 m，深度值d=50 m；目标为绝缘圆柱体，长L=5 m、底部半径R=0.25 m，当目标存在时，其深度值zt=-45 m；海水深度h=60 m，海床厚140 m；海水电导率σ1=4 S/m，海床电导率σ2=0.1 S/m；发射电极的电流为DC10A。

另外，为衡量两种方式计算结果的相似度，将模型计算值Uj与边界元仿真值U1j之间的误差γ定义如式(10)所示，误差越小，相似度越高，其中N为待比较值的个数。

(10)

2.2 一次场模型验证

因为在发射电极附近，电场分布具有较强的非线性，所以文中以两个发射电极中间50 m区域范围内的电场分布作为评价标准，利用式(10)计算文中模型与边界元仿真结果之间的误差。主要对比了两个发射电极之间目标不同深度(z方向)、不同偏移距离(y方向)时的电场值误差，如表1所示，注意当误差小于0.1%时，文中将误差视为0。

表1 不同深度、偏移距离对建模误差的影响

由表1可知，在不同深度、偏移距离的情况下，根据文中的一次场模型计算得到的水平电场Ex和Ey与边界元仿真结果高度一致，而垂直方向电场与边界元仿真结果存在一定的误差，主要是因为Ez更容易受浅水环境的影响，但是均小于12%，基本能够满足要求。

2.3 二次场模型验证

主动电场作用下，目标周围的扰动电场分布，属于二次场模型。首先应根据1.1节的一次场模型，计算出无目标状态目标对应位置处的电流密度分布；之后在有目标状态下，求出目标位置处所诱发的二次偶极子的电偶极矩；然后计算目标正下方不同深度平面的电场扰动值。

设定目标中心处于z=-45 m平面，为方便计算，使其轴向与y轴平行。将圆柱体目标沿y轴等分为m=10个圆柱单元，求出每个单元的y轴坐标为[-2.25 -1.75 -1.25 -0.75 -0.250.250.751.251.752.25 ]m，之后利用1.2节的电偶极子模型，求出每个圆柱单元位置处的电流值水平分量jx=[2.518 2.52 2.522 2.523 2.524 2.524 2.523 2.522 2.52 2.518] mA/m2，利用式(8)求出每个圆柱单元对应的电偶极矩，最后利用式(9)求出测线(y=0 m,z=-50 m)上的扰动电场分布。

求得测线上的扰动电场水平分量ΔEx和垂直分量ΔEz与边界元仿真结果的对比如图3和图4所示，利用式(10)求得它们的误差分别为1.54%和5.7%。

图3 扰动电场ΔEx(z=-50 m)Fig.3 Disturbed electric field ΔEx(z=-50 m)

图4 扰动电场ΔEz(z=-50 m)Fig.4 Disturbed electric field ΔEz(z=-50 m)

继续研究其他深度平面上的ΔEx和ΔEz与边界元仿真结果之间的误差，结果表明ΔEx误差基本处于3%范围内，ΔEz误差基本处于8%范围内。ΔEz误差相对较大的主要原因如下：①由于电流垂直分量jz远小于水平分量jx，计算时忽略了jz，未计算垂直方向二次电偶极子；②ΔEz相比ΔEx在垂直方向上受界面效应影响明显。

不同深度平面上ΔEx和ΔEz与边界元仿真计算值的峰值差异如图5和图6所示。可以看出，在靠近发射电极时，ΔEx和ΔEz的模型计算值分别大于和小于仿真值，主要是由于发射电极附近电流较大，非线性较强，利用一次场模型计算水

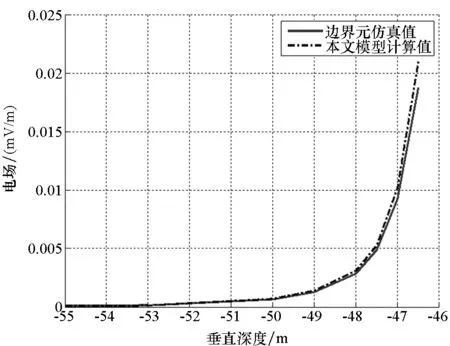
图5 不同深度平面ΔEx峰值对比Fig.5 The max value of ΔEx at different depths

图6 不同深度平面ΔEz峰值对比Fig.6 The max value of ΔEz at different depths

平和垂直电流密度jx、jz时误差增大，导致在计算二次场时，误差增大明显。

文中所建立的非金属圆柱体目标附近的扰动电场分布模型(即二次场模型)，相比于边界元仿真结果，扰动电场水平分量ΔEx误差均小于3%，而垂直分量ΔEz误差均小于8%。由于所研究的主动电场探测方法重点关注扰动电场水平分量ΔEx，所以文中所建立的模型能够满足要求。

3 水池模型实验

3.1 实验条件搭建

为进一步检验所建立模型的准确性，在实验室水池(1.6 m×1.0 m×1.1 m)进行实验，人工海水深度0.8 m，电导率1.25 S/m。实验中采用石墨电极作为电流发射端，发射电极之间水平距离0.8 m，深度0.4 m，各自距离水池边界0.1 m；采用Ag/AgCl电极作为测量电极，电极之间的距离为8 cm，电极静态压差小于0.1 mV;采用PVC管(Φ11 cm×30 cm)作为非金属目标，两端封口，目标中心深度0.25 m。

(a) 电极阵列(a) Electrode array

(b) 目标(b) The target图7 水池模型实验示意Fig.7 Schematic diagram of pool experiment

3.2 扰动电场测量及分析

事实上，电路所采集的只是每对Ag/AgCl电极之间的电位差Δφi(i=1,2,3)，由于电极之间的距离较短且已知，若将每对测量电极之间的电场视为均匀的，则可通过电位差Δφi简单计算出电场值Ei，所以图7及文中以电场值来表示。

实际实验中发现，当使用方波信号作为主动电场激励源时，测量电极测得的电场值存在较大的波动性，难以确定采样时刻，所以文中利用1 Hz正弦波代替，重点采集波峰和波谷对应状态的电场值及电流。首先测量无目标状态的初始电场值E1、E2、E3，同时测量对应的电流值；然后，在有目标的情况下进行相同实验，目标中心高于测量电极15 cm；之后将有目标状态的电场峰值减去无目标状态的电场峰值得到扰动电场峰值；最后根据电路板放大倍数及测量电极间距求得真实扰动电场值ΔEi(i=1,2,3)，如表2所示。另外，实验过程中发现电流峰值I在有、无目标状态下的差异低于1%，所以可认为电流值恒定，表2中电流峰值3.88 mA和7.98 mA分别对应信号源电压值1 V和2 V。

表2 不同发射电流对应的扰动电场峰值Tab.2 Peak value of disturbed electric field corresponding to different currents

利用边界元软件和文中建立的模型，按照水池实验的参数，计算目标中心下方15 cm处的扰动电场值分布，并与水池实验结果进行对比。图8为水池模型实验、边界元仿真和文中模型所求的结果对比。

(a) I=3.88 mA

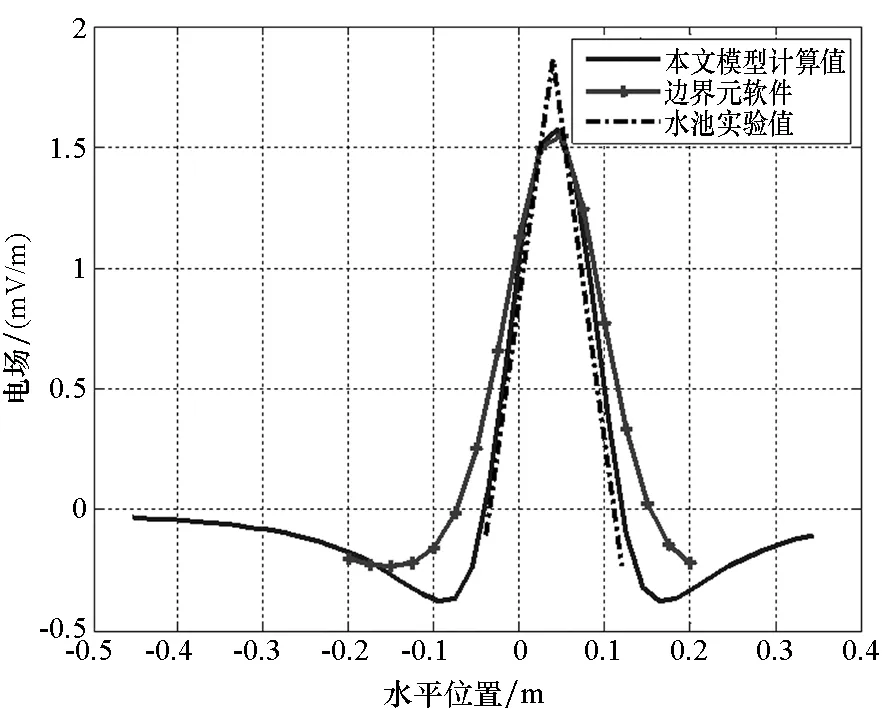
(b) I=7.98 mA图8 实验数据与模型计算结果对比Fig.8 Comparisons between experimental data and model calculation results

由图8可以看出，水池模型实验的结果与本文所建立模型的计算结果、边界元软件的仿真结果趋势一致。虽然文中只测量了目标正下方3个位置处(x分别为-0.04 m，0.04 m，0.12 m)的电场值，但是可以看出在3个测量点电场值基本与模型计算值相近。在目标中心位置处，水池实验得到的电场值明显高于模型计算值，除了测量误差外，主要是因为距离目标太近，扰动场分布非线性较大。

4 结论

基于镜像法和网格化思想，建立了浅海环境下非金属圆柱体目标的扰动电场模型，并与边界元仿真结果进行对比，结果表明文中所建立的扰动场模型具有较高的精度(扰动电场水平分量误差小于3%，垂直分量小于8%)。为进一步验证模型的准确性，在水池进行了模型实验，实验所测得的实际扰动电场分布与模型计算结果相近，在测量点位置处误差较小。

所建立的非金属圆柱体目标的扰动电场模型具有方法简单、计算量小的特点，相比于边界元求解，能够大幅提高计算效率，对于预测非金属目标所产生的扰动电场分布以及判断探测距离具有一定意义。