基于脉搏波特征参数的无创连续血压测量研究进展

郑嘉强，程云章，边俊杰

1.上海理工大学上海介入医疗器械工程技术研究中心，上海200093；2.浙江善时医疗器械有限公司，浙江杭州310016

前言

据2018年中国心血管病报告显示，中国心血管病患病率和死亡率仍处于上升阶段；报告推算心血管病现患人数2.9 亿，其中高血压2.45 亿。也有相关调查显示心血管病的死亡率居首位，高于肿瘤及其他疾病，占居民疾病死亡构成的40%以上［1］。有研究表明高血压人群会增加不同心脑血管疾病的发病风险，其中，收缩期及舒张期高血压增加幅度更大［2］。根据中国高血压调查研究结果，中国≥18 岁成人高血压的知晓率、治疗率、控制率和治疗控制率分别为51.6%、45.8%、16.8%和37.5%，我国的高血压防治工作仍面临着严峻的挑战［3］。高血压属于慢性病，诊断治疗需要一个缓慢、长期的过程，需在家调理、服药并长期监测［4］。连续血压测量可以实际反映血压在全天内的变化规律，对突发性心脑血管病的预测及对降压药的治疗效果评估有重要意义［5］。近年来，很多研究者对基于脉搏波特征参数的无创连续血压测量进行研究，本研究首先介绍脉搏波特征参数的类型以及基于脉搏波特征参数进行血压测量的原理，然后总结相关的测量模型，并分析各个模型的优缺点，最后对今后的研究方向进行总结和展望。

1 测量原理及脉搏波特征参数

1.1 测量原理

脉搏波特征参数测量法是在分析脉搏波特征参数与动脉血压相关性的基础上建立血压模型，实现连续血压测量的方法。血压的主要影响因素包括每搏输出量、心率、外周阻力、主动脉和大动脉管壁的弹性、循环血量与血管容量，这些因素的改变会导致血压的变化。了解影响血压的生理因素后，就可以通过测量反映这些生理因素的参数来间接反映血压的变化。

脉搏的变化是动脉内血压变化的反映，这是可以使用脉搏波进行血压测量的基本理论依据［6］。汤池［7］、欧辉彬［8］和Visvanathan 等［9］已分别从生理上详细分析脉搏波特征参数与人体血管外周阻力和血容量的相关关系，说明可以利用脉搏波相关的波形特征参数估计血压［10］。脉搏波从心脏开始向外周的动脉系统传播的过程中，脉搏波的形态不仅受到心脏本身的影响，也会受到各级动脉及其分支的各种生理因素如血液粘度、血管壁弹性及血管阻力等的影响，因此脉搏波中含有心血管系统的大量生理、病理信息，在临床上被广泛用于各种生理参数如血压、血氧饱和度、心率、心输出量、动脉顺应性等的测量和评估［11］。

1.2 脉搏波特征参数

脉搏波特征参数包括时域特征参数和频域特征参数。脉搏波时域特征参数可分为幅度参数、时间参数和面积参数。常用的脉搏波时域特征参数如图1所示。包括常用的幅度参数有主波高度（H1）、降中狭高度（H2）、重搏波高度（H3）、重博幅度（H4）等；常用的时间参数有主波上升时间（t1）、收缩期时间（t2）、舒张期时间（t3）、脉搏波周期（T）等［12］；常用的面积参数包括脉搏波面积、收缩期面积占比、舒张期面积占比、脉搏波波形系数K［13］等。

脉搏波频域特征参数是在脉搏波的幅值谱中提取。在对单个周期的脉搏波波形进行10次周期延拓后，对延拓后的波形进行快速傅里叶变换得到脉搏波幅值谱（图2）［14］。有研究表明，脉搏波的频谱成分主要集中在基波到5～6次谐波内［15］。

2.1 线性模型

2.1.1 一元线性回归模型基于脉搏波特征参数测量血压的一元线性回归模型是通过提取脉搏波信号中的特征参数，对特征参数与血压进行相关性分析，挑选出与血压相关性最好的一个特征参数，以该参数作为自变量，血压作为因变量做一元线性回归分析，建立一元线性回归方程进行血压测量的方法，其模型为：

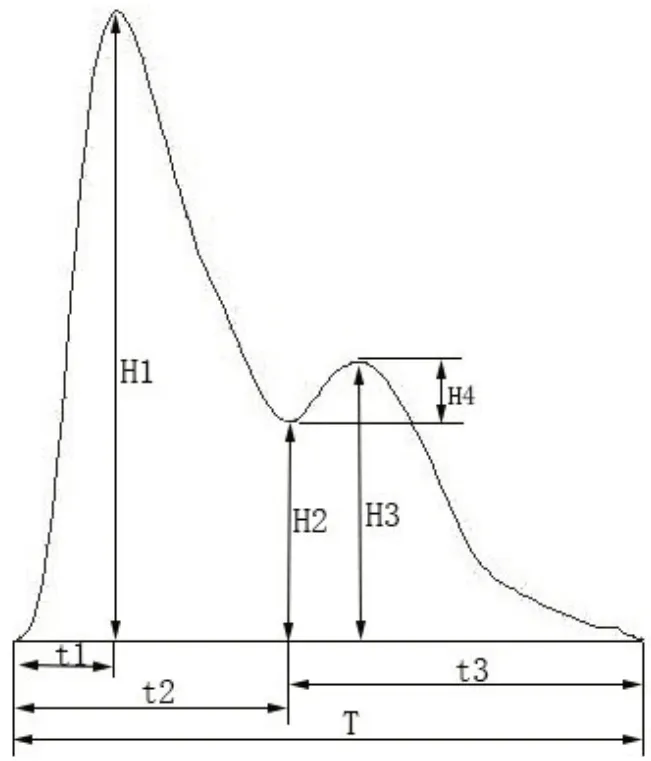
图1 常用的脉搏波时域特征参数Fig.1 Common characteristic parameters of pulse wave in time domain

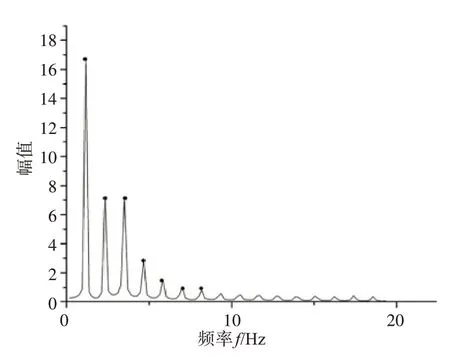
图2 脉搏波幅值谱Fig.2 Amplitude spectrum of pulse wave

其中，Y为血压值；X为选择的特征参数；a0为常数项；a1为回归系数；ε为随机误差项。

Teng 等［16］利用反射式光电容积脉搏波（Photoplethysmography,PPG）传感器获取PPG 信号，从PPG 信号中提取2/3 脉搏波振幅宽度（width1）、1/2脉搏波振幅宽度（width2）、收缩期向上搏动时间（T1）、舒张时间（T2）这4 个特征参数，并将这些特征参数分别与血压进行相关性分析，结果显示舒张时间（T2）与血压的相关性高于其他特征与血压之间的相关性。使用T1、T2 及PTT（ECG 信号R 波峰值到PPG信号峰值点之间的时间间隔）分别与血压建立一元线性回归模型，结果比较如表1所示［16］，该研究结果表明可以使用PPG 信号的舒张时间（T2）估计血压，且其精度与使用PTT估计的血压值精度相当。

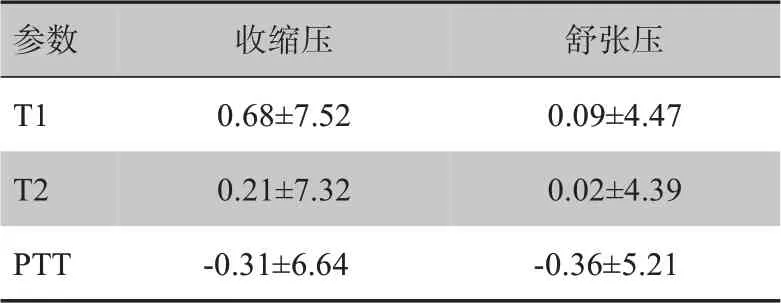
表1 使用T1和T2及PTT进行血压估计的平均数和标准差（mmHg）Tab.1 Mean and standard deviation of blood pressure estimations using T1 and T2 and PTT(mmHg)

也有研究从PPG 信号和心电信号中提取了5 个参数，分别为：心电R 波峰值点至PPG 一阶导数最大值点的脉搏波传播时间（PTT_dp）、心电R 波峰值点至PPG信号起点的脉搏波传播时间（PTT_foot）、心脏收缩时间（Sys t1）、心脏舒张时间（Dia t2）、2/3脉搏波振幅宽度（2/3 wt）［17］。通过相关性分析及对建立的一元线性模型进行误差分析，证明使用Dia t2 比使用PTT_dp或PTT_foot进行血压估计的精度更高。

2.1.2 多元线性回归模型血压的形成及影响因素复杂，仅用单一特征参数无法很好地描述血压的形成及变化，针对此问题，许多研究者对血压的多元线性回归模型进行了研究。仅提取脉搏波特征参数或提取脉搏波特征参数及其他相关参数如脉搏波传导时间和心率等，经过简单相关性分析或逐步回归分析等方法选择多个与血压相关性较大的参数，建立多元线性回归方程，进行血压的测量。其模型为：

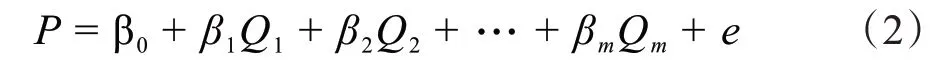
其中，P为因变量，为Q1，Q2，…，Qm的线性函数；Q1，Q2，…，Qm为自变量；β0为常数项；β1，β2，…，βm为偏回归系数；e为残差。

有研究从PPG 信号及心音信号中提取了脉搏波传导时间PWTTPCG、每搏心输出量Z、脉搏波波形系数K、升支平均斜率k、上升支波图与整体波图面积比值S、脉率HR 等参数，然后通过建立多元线性回归模型进行血压的估计［18］。基于PWTTPCG的单一参数血压计算模型和多脉搏波参数的人体血压计算模型计算得到每组测试者的血压值与实测值的平均误差见表2。对54 名测试者按照年龄段分成3 组，第一组年龄22～30 岁，共24 名测试者（14 名男性，10 名女性）；第二组年龄31～40 岁，共15 名测试者（9 名男性，6名女性）；第三组年龄41～46岁，共15名测试者（9名男性，6 名女性）。该研究结果显示，与单一参数的人体血压计算模型相比较，基于多脉搏波参数的人体血压计算模型在收缩压和舒张压测量中具有更高的准确性。但该研究在选择参数时仅用简单相关性分析，选出的参数可能具有多重共线性。

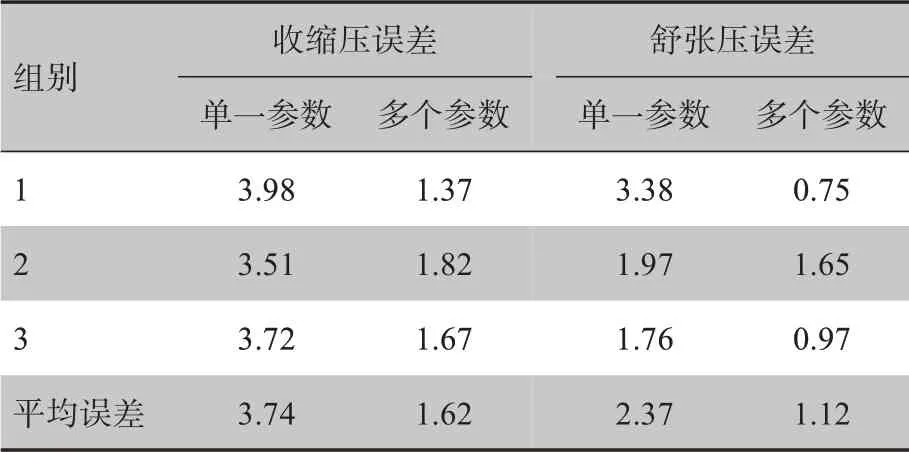
表2 计算得到的血压值与实测值的平均误差（mmHg）Tab.2 Average error between calculated and measured blood pressures(mmHg)

有研究提取了人体肱动脉脉搏波的13 个特征参数，包括时间参数、幅度参数和面积参数，通过逐步回归分析，得到具有个体差异性且与血压相关性较好的参数，由此建立针对个体的不同的血压特征方程［19］。在选择参数时采用逐步回归分析，可以保证留在模型中的特征参数既是重要的，且没有严重多重共线性，该方法建立的模型仍具有个体差异性。

有研究者对逐步回归法进行了改进，提出动态估计方法，通过改进的逐步回归算法动态实时估计连续血压［10］。通过设置滑动窗口，估计某时刻的血压时，选择该时刻前面最近的n组值做训练，逐步回归法做特征选择，估计该时刻的血压。通过该动态估计方法，可以进一步提高血压监测的精度和准确性。

前述研究中建立的模型多具有个体差异性，对不同人群进行血压测量时需要重新进行校准，建立的模型不具有普适性。针对目前利用脉搏波特征参数无法准确计算出病理如高血压、低血压的问题，可在选取特征参数时利用主成分分析法，对特征参数矩阵进行降维处理，基于较大的数据库建立多级血压计算模型，并通过逐步逼近缩小线性回归用到的样本区间，建立基于脉搏波特征参数计算血压的普适算法［20］。

2.2 神经网络模型

基于脉搏波特征参数的神经网络血压模型是通过选择脉搏波特征参数作为神经网络的输入，训练神经网络模型以进行血压的估算。选择的特征参数包括基本的脉搏波特征参数如时间参数、幅值参数和面积参数等，以及由脉搏波特征参数分解得到的特征参数或者整个脉搏波的波形数据。

血压的形成因素比较复杂，仅仅使用线性模型无法很好地描述出各参数与血压之间的非线性关系。为了使得模型更加接近实际，以达到更高的测量精度及更宽泛的适用范围，许多研究者引入神经网络模型以描述血压与脉搏波特征参数之间的非线性关系。常用的神经网络包括前向神经网络如反向传播（Back-Propagation,BP）神经网络［21-24］以及反馈型神经网络如简单RNN［25］、LSTM 模型［26］及Elman神经网络［27］等。

为解决使用线性模型不能很好地描述血压与脉搏波特征参数的非线性关系的问题，有研究者提出使用神经网络与脉搏波信号特征结合的方法来建立连续血压测量模型［26，28］。文献［28］从脉搏波信号中提取了21个脉搏波时间参数，用于训练BP神经网络。通过与血压的线性回归模型进行对比研究发现，仅仅使用舒张时间与血压之间的线性回归模型无法达到美国医疗器械促进协会（AAMI）的要求，而使用BP神经网络模型则能达到较高的精度，该模型预测的收缩压和舒张压为（3.80±3.46）和（2.21±2.09）mmHg，均满足AAMI标准。

前馈型神经网络虽然考虑了脉搏波特征参数与血压之间的非线性关系，但未考虑脉搏信号的时序连续性，即在建立的血压模型中未考虑到上一时刻脉搏信号的搏动对于后续血压的影响。为克服前馈型神经网络的这一缺点，有研究者将反馈型神经网络用于血压估算［25，27］。文献［27］选取脉搏波形起点、峰值点、降中峡这3个特征点作为连续血压预测模型的特征输入，利用反馈型Elman神经网络模型建立连续血压测量模型，并选用MIMIC 数据库中的大量数据来验证Elman神经网络的血压非线性预测能力，将其与BP 神经网络进行对比分析发现，Elman 神经网络在连续血压测量的准确度和预测精度方面都有一定的提高。

上述研究仍然存在特征点难以提取及模型不具备普适性等问题。针对此问题，有研究者提出一种新型卷积递归神经网络血压模型CRNN-BP［29］。该模型混合卷积神经网络和递归神经网络。使用一维卷积对各心动周期脉搏波的波形特征进行自动提取，不再依赖对波形特征点的定位，对不同形态的脉搏波波形具备普适性。使用递归网络层依据连续心动周期血压变化关系对波形特征进行校正，可减少个别心动周期波形受到干扰而影响血压预测精度的问题。通过MIMIC数据库中大量数据对该算法进行验证，结果显示与卷积神经网络血压（CNN-BP）模型相比，CRNN-BP模型的鲁棒性和精度更高。其预测收缩压和舒张压为（2.71±3.40）和（1.41±1.90）mmHg，达到了很好的精度和准确性。

3 总结与展望

当前基于脉搏波特征参数的无创连续血压监测尚处于实验室研究阶段，尚未有成熟的产品。使用脉搏波特征参数与血压建立的回归方程不能够从本质上反映脉搏波与血压变化的相关关系，也没有一个完整的数学模型能反映血压与脉搏波特征参数之间的关系［30］。因而当前只能采用统计学方法对其进行研究，如线性回归分析、神经网络方法等。

本研究总结了当前基于脉搏波特征参数的无创连续血压测量模型。主要包括一元线性回归模型、多元线性回归模型和神经网络模型。一元线性模型是通过提取脉搏波中与血压相关性最大的特征参数与血压建立回归模型，由于选取的参数单一，而血压的形成及影响因素较为复杂，一元模型不能很好地表征这种相关关系。进而有研究者引入了多元线性回归模型，选择多个与血压相关性大的参数与血压进行回归分析，进行血压估算，但这种模型仍难以描述脉搏波特征参数与血压之间的复杂非线性关系。

建立血压与脉搏波特征参数之间的非线性模型，并将神经网络模型引入血压估算中，能够达到较好的结果。当前建立的各种神经网络模型多具有个体差异性，对于不同的测量者建立的模型是不一样的。针对当前研究存在的问题，以后的研究方向是：（1）脉搏波及其脉搏波特征参数的准确提取，以减小数据源误差，提高血压测量精度；（2）普适性的血压模型研究，使得模型能够用于健康人、高血压和低血压患者的血压测量；（3）与侵入性血压之间的临床对比研究，以确定其临床实际精度和准确性。