液体核磁共振中多核体系的量子模拟

黄珊珊，李鹏，何培忠

1.上海理工大学医疗器械与食品学院，上海200093；2.上海健康医学院医学影像学院，上海201318

前言

核磁共振（NMR）技术是用射频脉冲激发处在外磁场中具有自旋的原子核，使之在相邻能级间发生共振跃迁，采样得到一个自由感应衰减（Free Induction Decay,FID）信号，经过傅里叶变换得到频谱图，用来测定物质的化学结构［1］。NMR 谱图中主要包含3个信息：化学位移、耦合常数、谱线的积分面积，其中耦合常数是自旋核之间磁相互作用大小的量度，在图谱中表现为特征谱线裂分形成的多重峰。多核自旋体系中相邻两核之间的核磁矩通过化学键传递产生的间接相互作用称为J 耦合［2］，耦合常数包含自旋核之间化学键的相关信息，是NMR 波谱技术中解析分子几何结构的重要依据［3］。液体NMR中分子的随机运动平均了直接耦合作用，J 耦合作用是液态物质特征谱线裂分的主要原因［4］。

量子模拟利用量子力学原理构建量子系统来模拟实际实验，可从模拟数据中提取相关的参数信息，用于设计新的实验和促进理论研究的发展［5］。核自旋系统是一个系综［6］，其量子初态和整个演化过程遵循量子力学原理，使用数值计算方法对一个NMR 实验进行量子力学建模，理论上可得到与实际实验一样的结果。目前比较成功的NMR 模拟程序有GAMMA［7］、SIMPSON［8］、SPINEVOLUTION［9］，它们的共同点是使用哈密顿算符来表示NMR 中任一时刻的全部相互作用，从量子初态出发到最后采样，得到一个FID信号，再做傅里叶变换获得与实际实验结果十分相近的谱。在物理学原理上，磁共振成像（MRI）和NMR 波谱是一致的，区别在于MRI 处于低场，而且临床上只对质子信号激发和采样，因此MRI也可用Bloch 矢量模型［10］进行解释。为了统一这两个场景的模拟，Chang等［11］发布了一个新的模拟软件Spin-Scenario，对NMR 和MRI 进行统一的量子力学模拟。上述模拟程序都能够模拟许多传统的NMR实验，且与实验结果高度吻合，在NMR 研究中得到广泛的应用［12］。但目前NMR 模拟最大的不足在于能够模拟的分子体系都非常小，而且尚无统一和有效的方法来解决分子快速运动问题。

自旋量子数为12 的原子核最适合且最常用于NMR 鉴定研究［13］，本文用量子力学观点描述液体NMR 中自旋量子数为12 的多核体系间的J 耦合作用，并将自旋系统的化学位移、耦合作用写入密度矩阵的演化方程，在MATLAB 2015b 软件平台模拟出方程演化结果以及所对应的NMR 谱图，整个计算过程完全遵循量子力学规律，模拟的结果是客观且精确的。

1 J耦合作用的量子描述

具有自旋的原子核在无外加磁场的环境中的自旋取向是任意的，磁性相互抵消，不具备宏观磁性。在外磁场B0中，自旋量子数为12 的核有了两种取向［14］，即自旋向上的低能态和自旋向下的高能态，两种状态的能量差为ΔE，如图1所示。

图1 自旋核能量状态Fig.1 Spin nuclear energy state

在NMR 中，与被观测核相邻的原子核的自旋扰乱了附近电子的自旋分布，进而扰动观测核的能级，由于扰动核的自旋具有两种状态，当自旋状态与观测核相同时观测核的能量对应地升高，当自旋状态与观测核相反时观测核能量降低［14］，最终在谱图上表现为被观测核谱线的裂分。

自旋量子数为12 的一对耦合原子核组成IS 系统，当外磁场B0平行于Z 方向，在垂直于B0的方向上施加角频率为ω的射频场B1，系统的哈密顿量为［14］：

其中，ωI、ωS分别为I核和S核的共振频率；Iz、Sz分别代表I核与S核在Z 轴方向的角动量算符；JIS是两核之间的耦合强度。

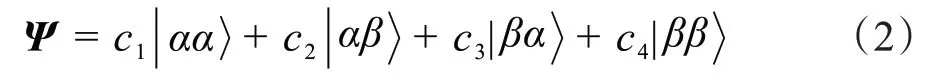
系数c1、c2、c3、c4是叠加系数，需满足归一化关系：

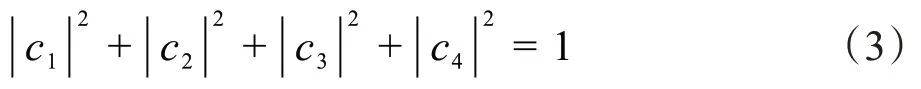
NMR 是自旋核相邻能级之间的能量跃迁，能级图如图2所示［2］。

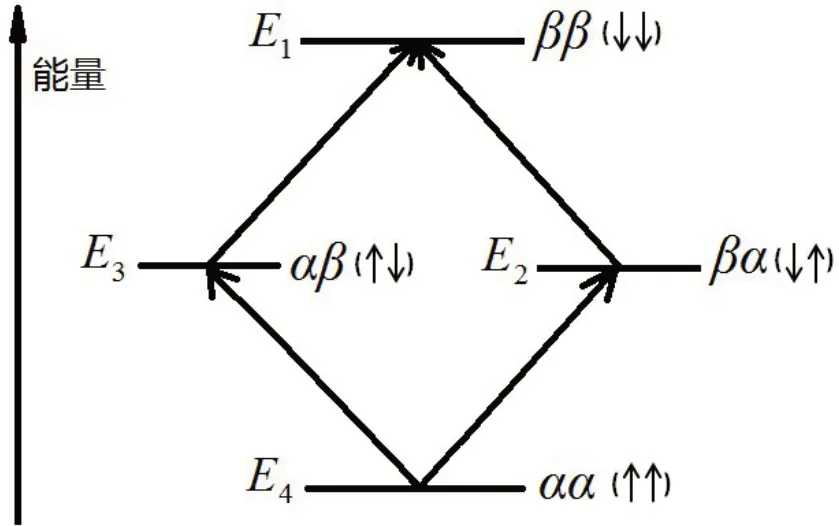
图2 双核自旋体系能级图Fig.2 Energy level diagram of a double spin system

对应的能量为：

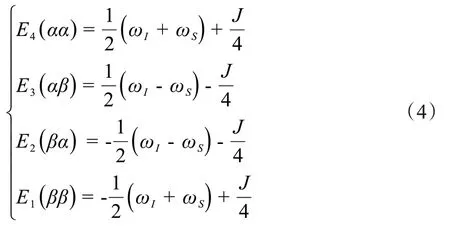
相邻能级之间跃迁的能量差为：

J耦合作用在NMR图谱中的表现如图3所示。

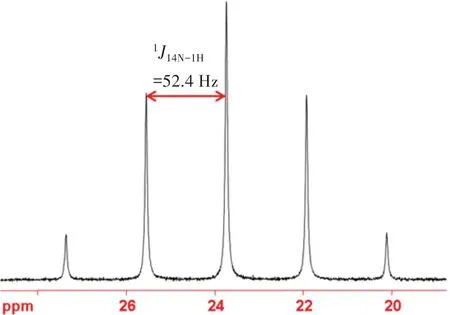
图3 NH4Cl的14N-NMR谱Fig.3 14N-NMR spectrum of NH4Cl

这是NH4Cl 的14N 核磁共振一维谱［15］，耦合常数在图中标记为1J14N-1H，表示14N与1H之间存在耦合，4个氢质子的耦合作用使得14N 的特征谱线分裂成五重峰。自旋量子数为12的原子核一维NMR谱的耦合规律如下［3］：观测核与n个磁等价的自旋核耦合时，产生n+ 1条谱线，谱线中心为观测核化学位移特征峰的位置，分裂谱线之间的距离记作耦合常数，单位为Hz，多重峰之间相对强度对应于(a+b)n展开式的各项系数。

2 IS体系的密度矩阵

NMR的自旋系综遵从量子力学中的刘维尔冯纽曼（Liouville-von Neumann）方程［16］，在模拟前需要将所有算符的矩阵形式都写出来。

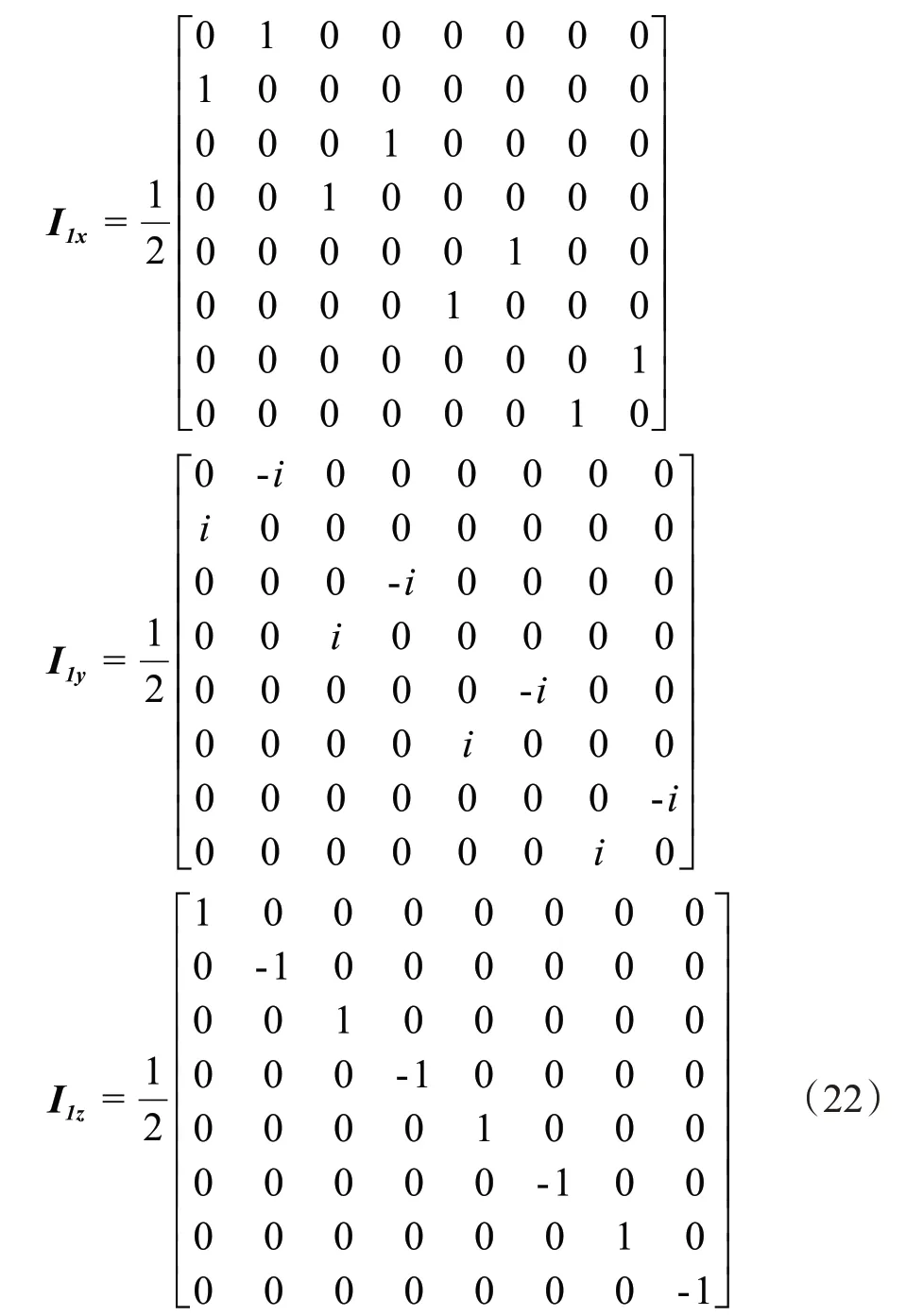
对于自旋量子数为12的单核自旋，用泡利矩阵表示它在各坐标方向的角动量算符［17］：

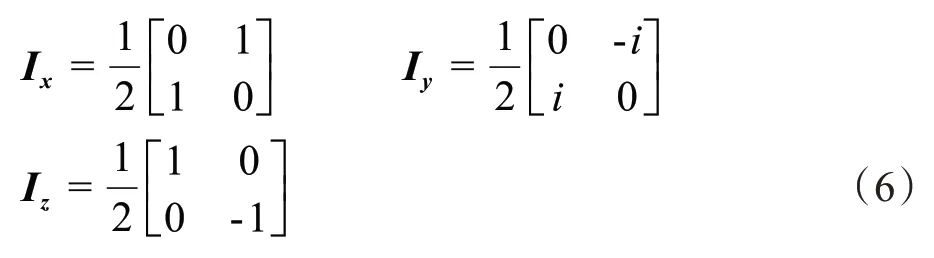
对于双核自旋系统，角动量算符的乘积算子可由单自旋矩阵与单位矩阵的张量积得到［18］，计算求得IS体系的角动量算符如下：

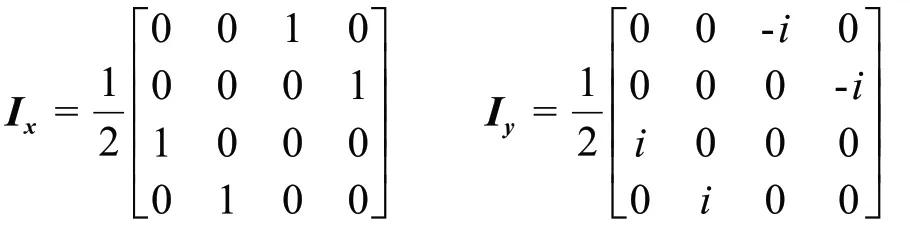
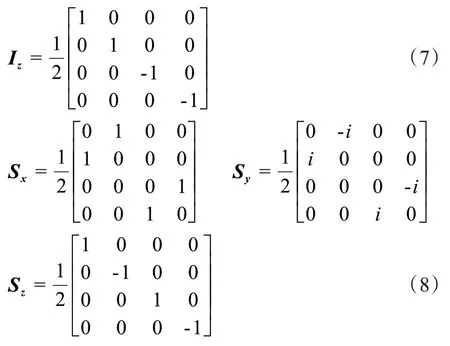
计算验证上述角动量算符满足归一化关系：

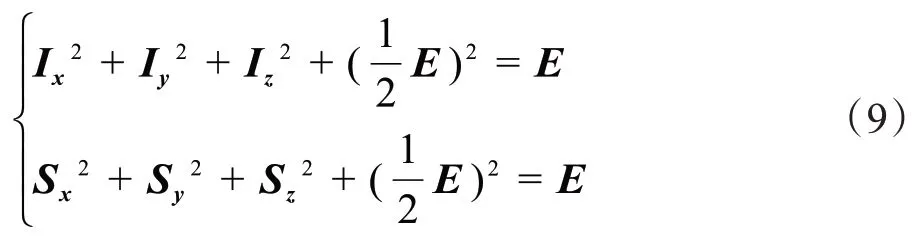
其中，E是单位矩阵，与自旋角动量算符共同描述密度矩阵的演化。自旋对的状态函数与系数组成4×4密度矩阵，矩阵元素提供了关于系统各种状态的信息，在哈密顿的作用下，每个元素所包含的信息随时间演化。

IS体系在Z方向初始状态的密度矩阵表示为［18］：

同理可证各矩阵其余元素的状态关系。

密度矩阵随时间演化的过程遵循如下演化过程［19］：

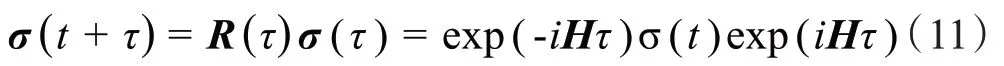
其中，σ(t)代表t时刻密度矩阵的状态，R(τ)是时间演化超算符，在式中表示哈密顿在τ时间段内对密度矩阵的作用。

密度矩阵包含自旋体系演化状态的全部信息，但是能被仪器检测到的只有单量子跃迁过程，I核与S核的信号分别用观测算符I+、S+来检测［14］：

在哈密顿的作用下密度矩阵的对角元代表自旋系统在对应本征态处的被发现的概率，通过计算密度矩阵与观测算符乘积的迹得到矩阵中特定的乘积算子，作为磁共振的信号。

3 多核体系的波谱模拟

3.1 双核体系波谱模拟

NMR 中，IS 体系在热平衡态时的密度矩阵记为σ0：

因IS 为异核体系，沿X 轴正方向对该系统施加90°脉冲激发I核共振，I核的激励脉冲对S核的密度矩阵无影响，此时IS体系的密度矩阵演化记作σ1：

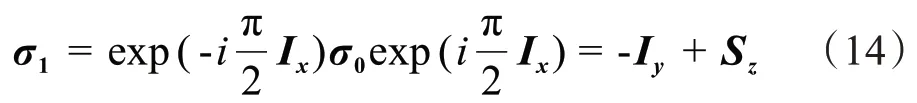
表示I核的磁化矢量在脉冲的作用下发生90°翻转，倒向-Y 轴，同时IS体系发生耦合作用，此时系统的哈密顿量为：

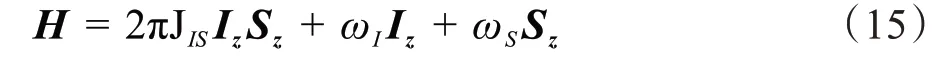
其中，ωI、ωS分别为I核与S核的共振频率；JIS为两核之间的耦合常数。在化学位移和脉冲的作用下I核开始自由进动和弛豫，角动量算符在空间中发生旋转，密度矩阵在哈密顿作用下演化的方程ρ()t表示为：

密度矩阵用I核的观测算符检测，此时得到的共振信号表示为：

式中tr表示求密度矩阵的迹。

考虑到液体中FID信号的衰减为洛仑兹线型，因此需对共振信号加上e指数窗函数模拟宏观信号［20］，最终的时域信号为：

以上就是IS 体系在单脉冲核磁共振模拟实验中密度矩阵演化的全过程。最终的FID 信号可通过设置采样参数进行信号采样，经过傅里叶变换得到模拟谱图。

以IS 异核体系的I核谱图为例，I核化学位移为400 Hz，耦合常数JIS=200 Hz，采样间隔为1 ms，采样时间t=1 s，窗函数的时间T=0.15 s。在MATLAB 2015b 软件平台进行数值模拟，得到的时域信号如图4所示。

信号进行傅里叶变换之后得到的模拟谱如图5所示。

从谱图中可知I核的单峰裂分为强度相等的二重峰，测得分裂峰之间的距离为200 Hz，波峰的中心为I核的化学位移400 Hz，模拟结果与耦合关系一致。

如果IS 是同核体系，则90°激励脉冲对两核均起作用，密度矩阵表示为：

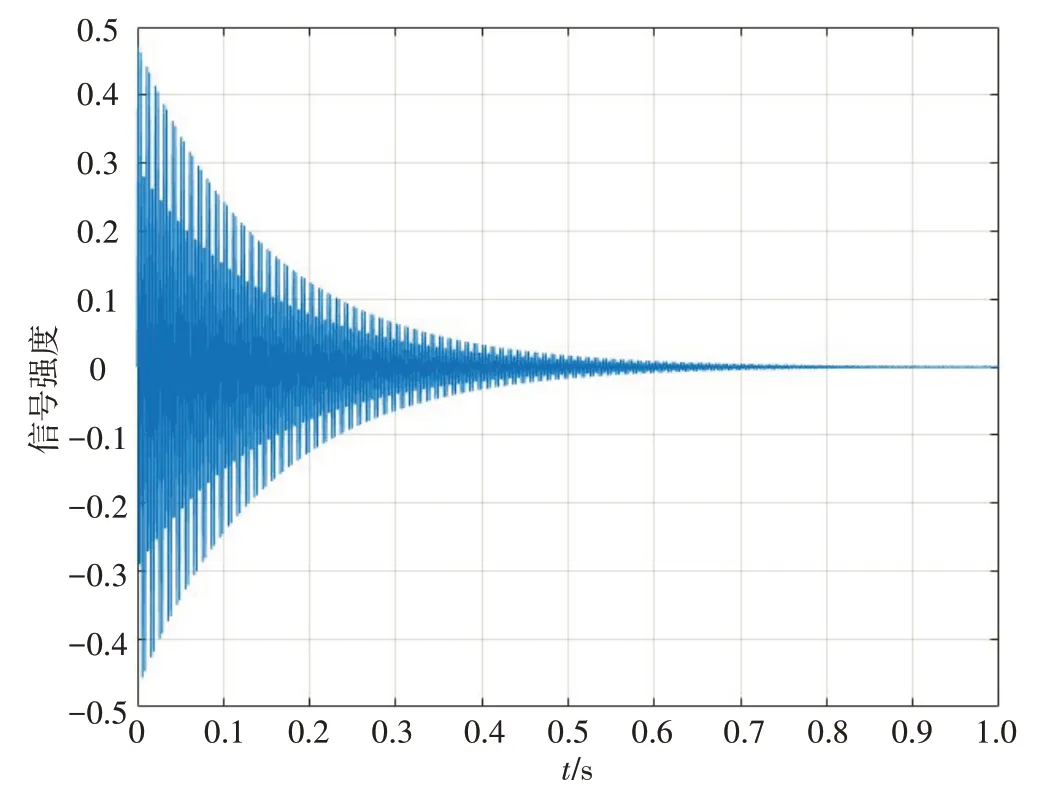
图4 I核的FID信号Fig.4 Free induction decay(FID)signal of nucleus I

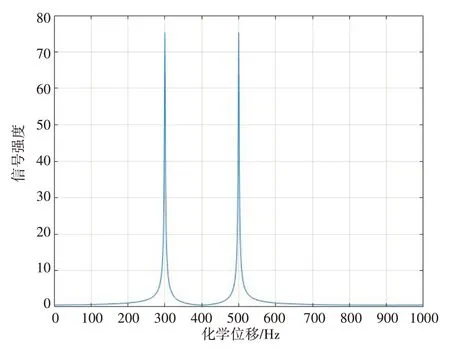
图5 I核的频谱Fig.5 Spectrum of nucleus I

I核与S核的磁化矢量均倒向-Y 轴，在耦合作用下系统的哈密顿与异核IS 体系保持一致，此时密度矩阵的演化方程：

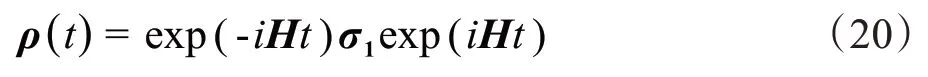
使用两核的观测算符，最后共振信号可表示为：

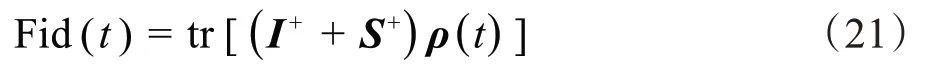
IS同核体系中，两个核处于不同的化学环境，I核的化学位移为200 Hz，S 核的化学位移为600 Hz，耦合常数JIS=30 Hz，采样参数设置与IS 异核体系波谱模拟一致，得到的时域信号如图6所示。信号经过傅里叶变换之后得到的模拟谱图如图7所示。

图6 IS核的FID信号Fig.6 FID signal of nucleus IS

图7 IS核的频谱Fig.7 Spectrum of nucleus IS

分析谱图可知，I核的特征峰中心在200 Hz 处，谱线裂分为强度相等的二重峰，波峰间隔为30 Hz；S核的特征峰中心在600 Hz 处，谱线也裂分为强度相等的二重峰，波峰间隔为30 Hz，模拟结果与耦合关系的描述一致。

3.2 三核体系波谱模拟

将自旋量子数为12 的3 个耦合原子核组成的体系记作I2S，其中I1、I2核是为自然丰度高的两个同类核，S核是自然丰度低的稀核。做S核的一维NMR谱时，I1、I2核对S核均有耦合作用，耦合常数分别记作J1S、J2S；I1、I2之间也存在耦合关系，耦合常数记作J12；3个核的共振频率分别记为ωI1、ωI2、ωS。

由IS 耦合体系的自旋算符推导，同理可得I2S体系各核的自旋算符矩阵，例如I1核各方向的角动量算符的矩阵分别表示为：

对I2S体系的S核作波谱模拟，沿X轴正方向对S核施加90°脉冲，此时系统的哈密顿函数为［13］：

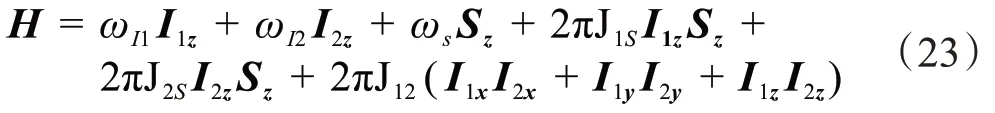
重复上文双核体系NMR 模拟的演化步骤可得到模拟信号。S核的化学位移为400 Hz，耦合常数J1S=J2S=100 Hz、J12=30 Hz；采样间隔为1 ms，采样时间设为t=1 s，窗函数的时间T=0.2 s。得到的时域信号如图8所示。

图8 S核的FID信号Fig.8 FID signal of nucleus S

信号进行傅里叶变换之后得到的模拟波谱如图9所示。

图9 S核的频谱Fig.9 Spectrum of nucleus S

图谱中，S核的特征峰中心在400 Hz 处，特征谱峰分裂为强度比为1:2:1 的谱线，分裂谱线与中心距离为100 Hz，模拟结果与描述的耦合关系一致，谱峰强度之比符合三核体系谱线耦合裂分的规律。

4 结束语

本文使用量子力学数值模拟算法，模拟了液体NMR 中多核体系的自旋动力学演化。首先将液体NMR 中自旋体系所涉及的相互作用写入哈密顿函数，并将哈密顿量作用于密度矩阵演化方程，精确记录密度矩阵在演化过程中的状态，采样所得的时域信号经过傅里叶变换得到谱图，分别模拟了两核和三核体系中的液体核磁共振实验，其结果与对应的理论预测及预期的实验结果一致。这种算法可推广到更高数量的自旋体系，可帮助研究人员理解NMR的物理学原理，也可以用于辅助分析真实的NMR实验。