拉盖尔-高斯光经超表面的聚焦特性

陈 同

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

激光光束经高数值孔径物镜聚焦后可在聚焦光场产生强烈的纵向分量和紧密聚焦光斑[1-4]。由于紧密聚焦光束具有独特的性质，使其在光学数据存储、显微镜、材料加工和光学俘获方面具有广泛的潜在应用[5-8]。因此，紧密聚焦光束的特性引起了学者的极大关注[9-11]。

随着人们对激光光束聚焦特性的深入研究，该特性在光学捕获、激光加工和高分辨率成像等方面的应用引起了人们的广泛关注。到目前为止，研究人员已经研究了各种光束，如圆柱矢量光束、涡旋光束、具有常规相关函数的部分相干光束的紧密聚焦特性[12-21]，还基于Richards-Wolf矢量衍射理论，研究了拉盖尔-高斯相关谢尔模型（LGSM）光束通过高数值孔径（NA）聚焦系统后的紧密聚焦特性，该结果可在具有非传统关联函数的部分相干光束的光阱中得到应用[22]。

目前对于拉盖尔-高斯光的研究是在传统光学透镜等光学元件的基础上进行的，主要是利用超表面对拉盖尔-高斯光的聚焦光场的电场强度和相位分布作一些基础研究。与此不同，本文通过时域有限差分（FDTD）方法仿真拉盖尔-高斯光经超表面的聚焦光场，通过改变入射光的偏振态以及超表面的数值孔径，研究聚焦光场的相位、纵向电场分量、总电场的分布特性。

1 聚焦原理

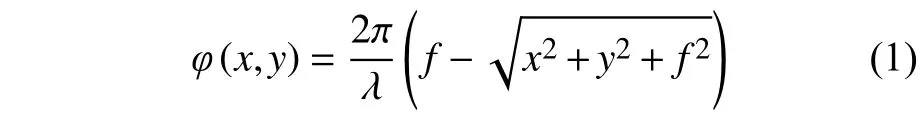
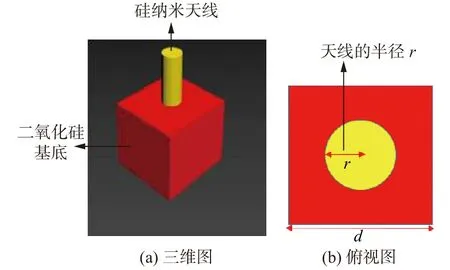
图1 天线单元Fig. 1 Side-view and top-view of the metasurface building block

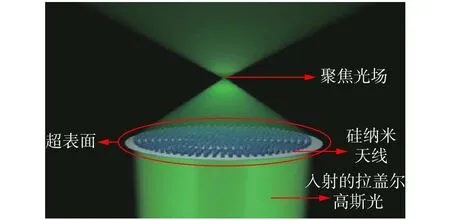
图2 超表面处于透射模式下的聚焦光场图Fig. 2 Focus field view of the metasurface operating in transmission mode

在一个圆形范围内按一定规则排列很多天线单元，组成一个能汇聚光束的超表面，如图2所示。通过调整天线的直径大小可以对聚焦光场实现所需的相位[23]，从而替代传统透镜对入射椭圆偏振拉盖尔-高斯光的聚焦功能，以及实现对聚焦光场特性的研究。

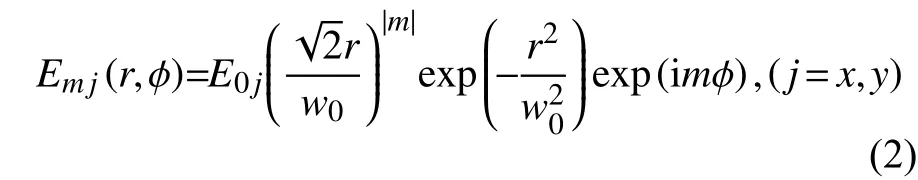
式中：m为拓扑核数；为光源的角向坐标，且分别为振幅和光束大小的常数。

当入射光束是椭圆偏振时，其拉盖尔-高斯光束可表示为

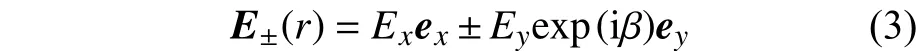
2 仿真结果和分析

图3为拓扑荷数m=1时左旋、右旋椭圆偏振拉盖尔-高斯光经数值孔径为0.90的超表面后的聚焦光场分布图。在左旋光入射的情况下，焦面处总电场强度、x分量电场强度、y分量电场强度分布与右旋光入射经超表面聚焦后的电场强度分布皆为一个暗核的涡旋光。在图3（d）的右旋光聚焦光场z分量中出现了两个暗核的涡旋光，相反在左旋光的聚焦光场中z分量电场没有出现暗核，此现象说明，在聚焦电场的z分量电场中出现了自旋角动量转化为轨道角动量的情况。图4为聚焦平面处电场相位图，其中（d）、（e）为左旋光在聚焦面处的x分量电场相位、y分量电场相位，对应的拓扑荷数m=1，（f）为左旋光在聚焦面处z分量电场相位，对应的拓扑荷数m=0 。对于右旋光，其在聚焦面处的x分量电场相位、y分量电场相位分布如图4（a）、（b）所示，对应拓扑荷数m=1，对于电场中心z分量电场相位，如图4（c）所示，对应的拓扑荷数m=2。由此说明，自旋角动量转化为轨道角动量发生在z分量方向。在非傍轴情况下，光束轨道角动量与单位能量比值为[24]

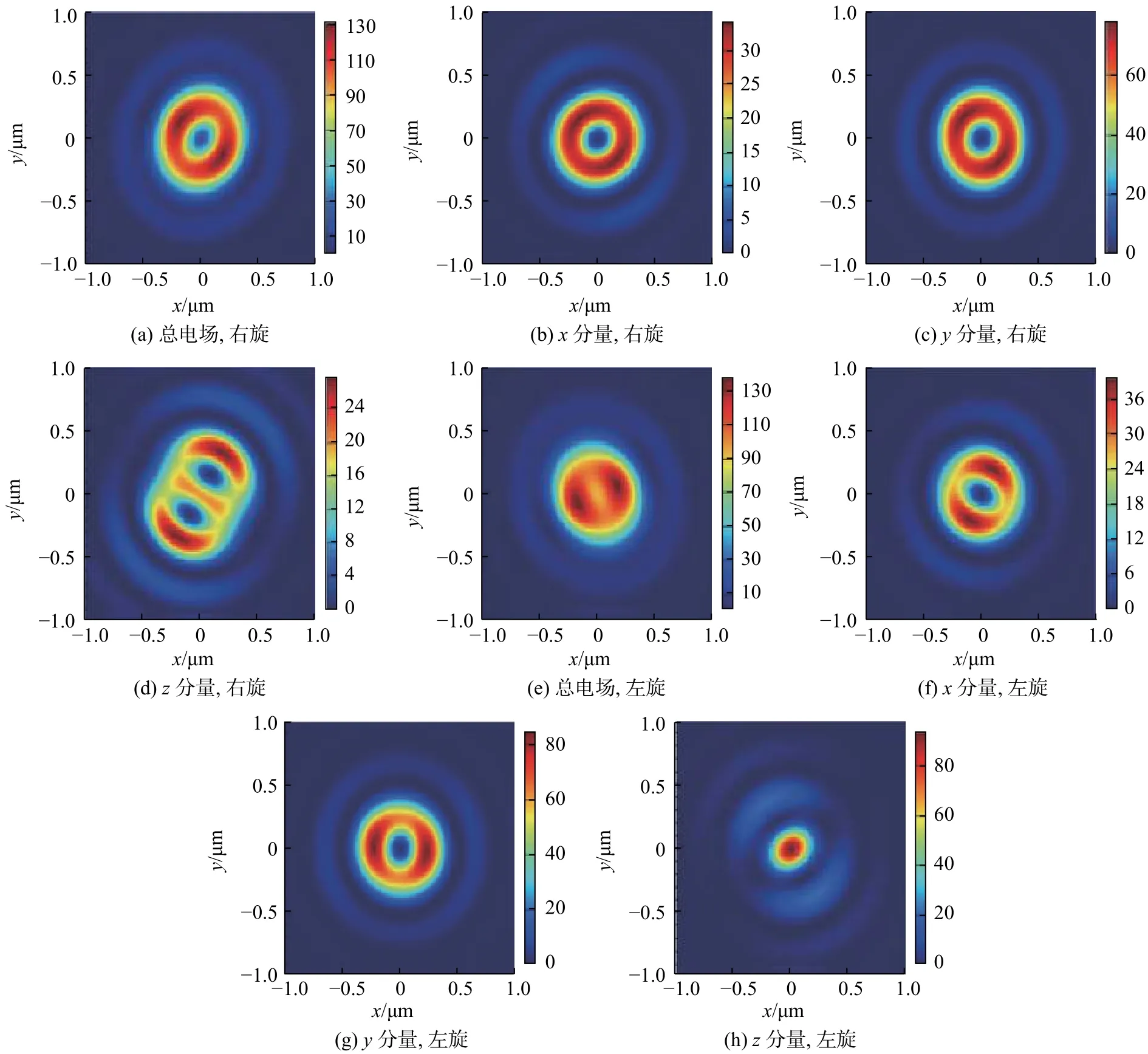
图3 不同极性光束在焦面电场强度分布Fig. 3 Intensity distribution in the focal plane for different polarization beam

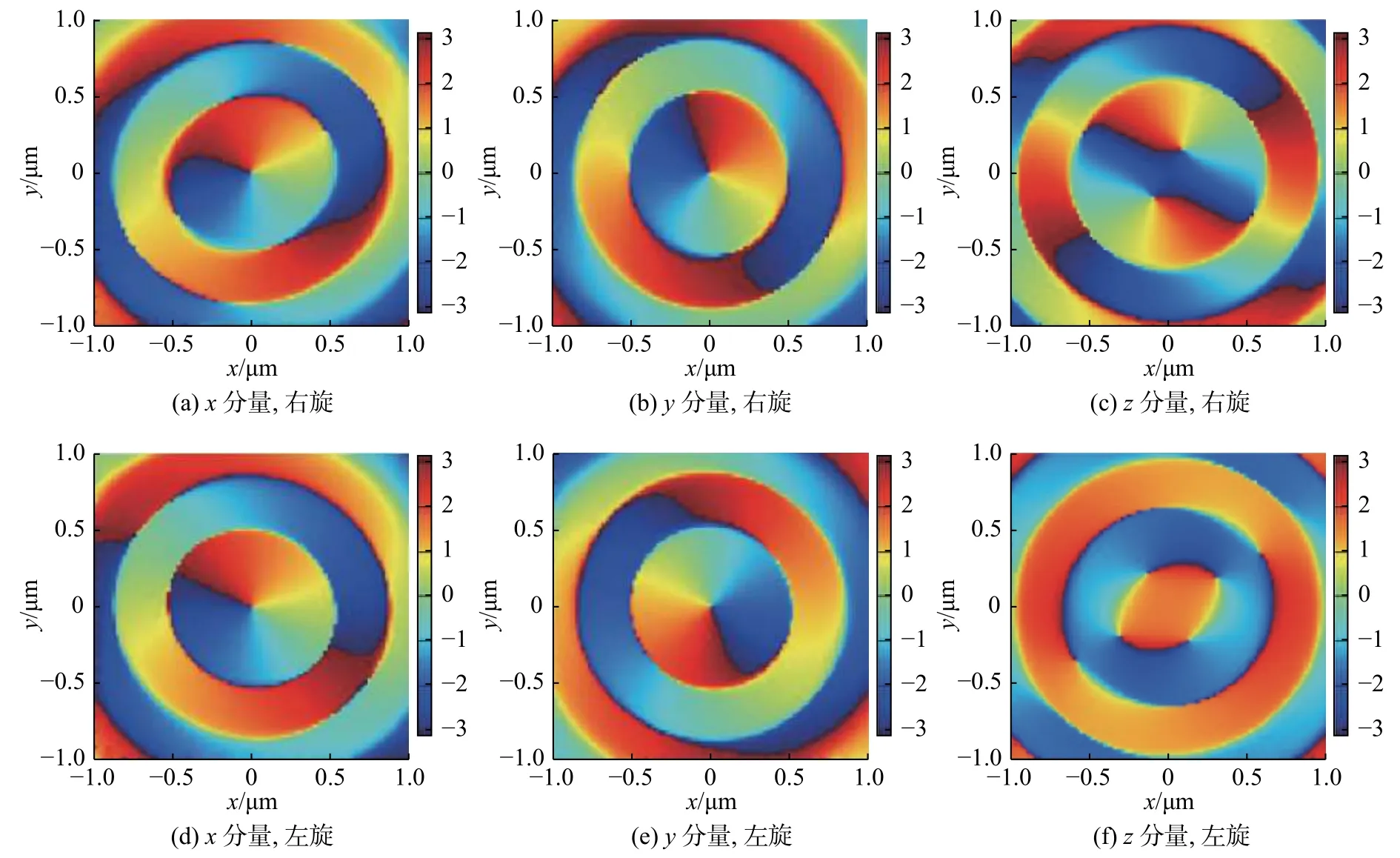
图4 焦点处的 x，y，z 分量相位分布图Fig. 4 Phase contours of the x,y and z components in the focal plane

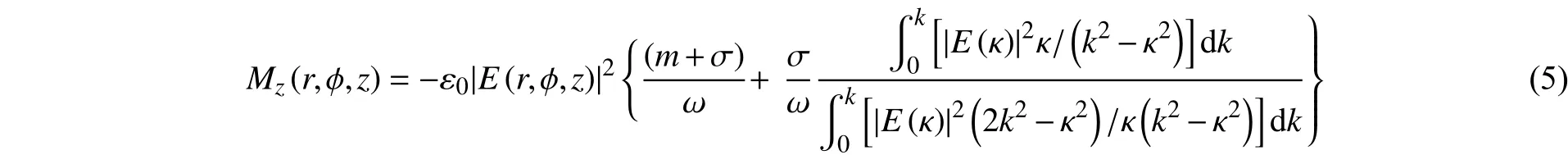
综合图3、图4、式（4）～（6）可知，由于入射光束自身携带的极性不同，导致自旋角动量在z分量电场处转化为轨道角动量。右旋光经超表面聚焦后，z分量电场的自旋角动量转化为与光束本身携带的轨道角动量相同方向的轨道角动量，从而使轨道角动量增强，使拓扑荷数m=2。左旋入射光经超表面聚焦后，z分量电场的自旋角动量转化为与携带的轨道角动量相反的轨道角动量，从而减弱了轨道角动量，使得z分量电场强度分布为实心光斑，轨道角动量的拓扑荷数m=0。

在焦面处放置偏振片，以过滤出聚焦光场中的左旋光和右旋光，如图5所示。从图5的左旋光电场强度与右旋光电场强度分布可知，超表面将入射的右旋光转化为电场强度最强的左旋光，圆柱型天线的超表面可以将入射的右旋光大部分转换为左旋空心的出射光，而含有少量比例的右旋空心光。从图5（a）、（b）可以看出，圆柱形超表面可改变入射光的偏振特性，通过超表面可得到不同形状的涡旋光，从而使出射的空心光对被出射光挟持的不同形状、大小的微粒自身旋转方向做出相应的调整。在实际应用中，拉盖尔-高斯光经超表面聚焦后的涡旋光场可以向被约束的微粒传输轨道角动量，通过紧密聚焦控制光束的轨道角动量有着广泛的应用，如可充当光学扳手等。

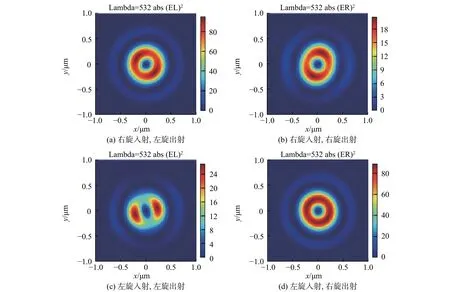
图5 焦面处过滤的不同极性光的总电场强度分布Fig. 5 Intensity distribution in the focal plane for different polarized beam after polarization filtering

拉盖尔-高斯光束经高数值孔径超表面的紧密聚焦相较于经低数值孔径的超表面的普通聚焦而言，紧密聚焦会在出射光场焦面处产生一个纵向电场分量，对此本文研究了入射光的相位差对纵向电场分量的影响。

图8为不同数值孔径下聚焦面的总电场分布，由图可见，随着数值孔径由0.80增大至0.95，空心光的形状由圆形逐渐变为椭圆形，而且空心面积也越来越小。该现象表明，数值孔径越大，超表面对入射光的紧密聚焦特性也越明显。因此，可以通过改变超表面的数值孔径的大小，调整出射光的形状。

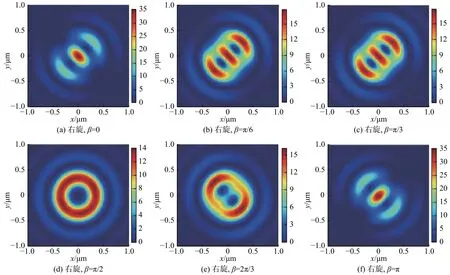
图6 不同相位差对应的聚焦面纵向分量电场强度分布Fig. 6 Distribution of electric field intensity of longitudinal component in the focal plane corresponding to different phase difference

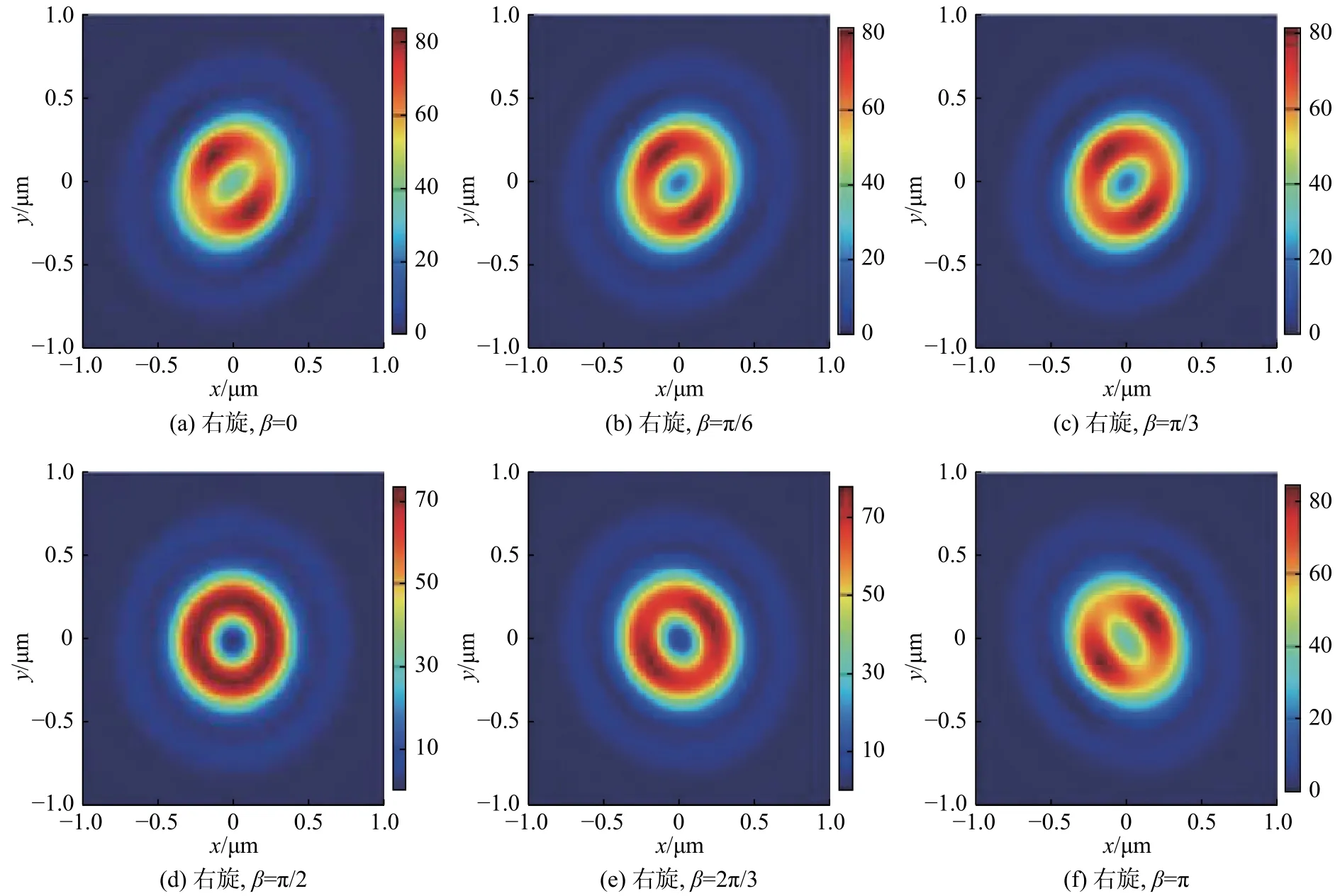
图7 相位延时对聚焦面总电场强度的作用Fig. 7 Influence of phase delay on the total electric field in the focal plane

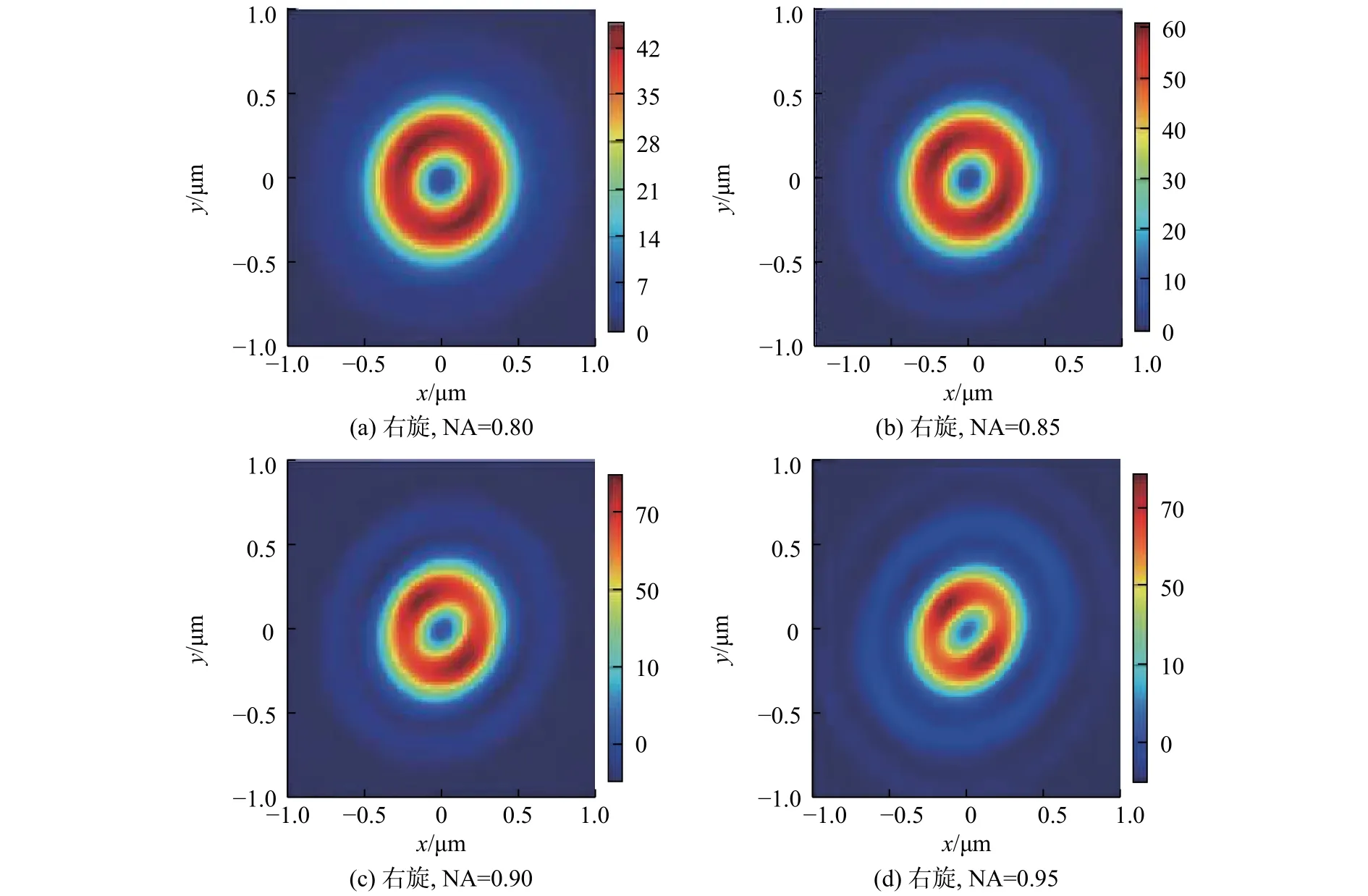
图8 数值孔径大小对聚焦面总电场强度的作用Fig. 8 Influence of varying NA on the total intensity in the focal plane

3 结 论

本文研究了拉盖尔-高斯光经超表面聚焦后的光场特性，采用FDTD方法模拟出聚焦光场z分量电场出现的自旋角动量转换为轨道角动量的现象。研究发现：通过改变入射光的自旋角动量可改变出射光纵向电场分量的拓扑荷数m的大小；调整入射光束的相位差以及超表面的数值孔径可以控制聚焦光场分布以及旋向。研究结果可为拉盖尔-高斯光在微流控、光镊、光学扳手等领域中更好的应用提供参考。