竞争合作行为下的深度演化算法*

陈海娟，冯 翔，2+，虞慧群

1.华东理工大学 信息科学与工程学院，上海200237

2.上海智慧能源工程技术研究中心，上海200237

1 引言

2017 年周志华等人提出的深度森林[1]引起了很大反响，它是一种基于决策树森林而非神经网络的深度学习模型，且它的性能可与深度神经网络相媲美。在深度学习中，它有多个隐层，具有表征学习能力，且有大量的数据去训练使得它的模型足够复杂[2-3]。文献[1]中指出，若能将这些属性赋予其他一些合适的学习模型，或许也能取得和深度神经网络类似的效果，但这并不是为了取代深度神经网络现有的地位，而是为了解决现有复杂的实际问题，就要深化学习模型，积极探索多样的深度模型。

近年来演化算法也取得了较大进展。如2008年，Simon 通过模拟自然界中的迁徙行为提出了迁徙算法（biogeography-based optimization，BBO）[4]；2013年，Cuevas提出社会蜘蛛算法（social spider optimization，SSO）来再现蜘蛛的社会行为[5]；2018 年，Alizadeh 等人通过人体免疫现象提出了人造免疫系统[6]等。虽然演化算法能解决一些优化问题，但本身却存在易陷入局部最优、过早收敛以及难以适用于复杂的实际场景等问题。受深度森林的启发，如果演化算法是一个合适的模型，将深度的概念引入到演化算法中，或许能提升演化算法的性能。基于此，本文将深度引入下面所提出的一种新的演化算法中，来探究深度与演化算法相结合的效果。

自然界中，大多数动物都分群而居[7]，物种之间及生物内部之间都存在生存竞争，能适应自然的才能留下来[8-9]。人类社会也是如此，帝国之间相互竞争，掠夺殖民地，在历史演变过程中，一些国家被历史淘汰，一些国家存活了下来，Atashpaz-Gargari等人通过对此研究提出了帝国竞争算法[10]。合作行为也是一种常见的自然行为，动物群体的集体智慧行为加强了个体之间的分工与合作，实现双方互利共赢[11-12]。Szathmáry 就曾说过“合作可以推动合作行为人口结构的演变”。受此启发，基于生物群模型、竞争模型以及合作模型，提出一种新的群体智能演化算法。

本文在新的群体智能演化算法中引入深度，相应的体现为多步迭代、特征变换以及模型足够复杂。首先，算法是深度迭代的，通常算法只经过一层迭代，本文算法有两层迭代，每层迭代多次来寻找最优解；其次，为了避免算法陷入局部最优，对生物群模型中的随机者引入特征变换策略[13-14]，搜索其他成员未搜索的方向，可有效发掘潜在最优值，避免算法陷入局部最优；再者，算法引入了生物群模型、合作模型、竞争模型以及变步长模型，使得算法有一定的复杂性。对于变步长模型，通过每次演化过程中个体移动步长的动态调整，可实现算法收敛速度和算法精度的均衡[15]。

基于上面的描述，本文主要有以下几方面的贡献：

（1）启发于周志华等人提出的深度森林[1]，提出将深度引入演化算法中；

（2）通过自然界中的分群和竞争合作现象，提出了生物群模型、竞争模型和合作模型，继而提出一种基于竞争合作的新的演化算法；

（3）在演化算法中引入变步长机制，平衡了算法收敛速度和算法精度；

（4）将深度引入所提出的基于竞争合作的演化算法中，在十个优化函数和实际问题中验证了所提深度算法的有效性。

2 生物模型

2.1 生物群模型

自然界中的大多数动物都是群居动物，它们分群而居，有一定的社会行为，在自然进化中，能适应自然者才能生存下来。

2.1.1 群分类

在群竞争合作优化（group competition cooperation optimization，GCCO）算法中，一个种族有N个群体，每个群体中有n个个体，每个群体有领导者、跟随者以及随机者这三种角色，每个角色在搜索猎物时有不同的搜索策略。

定义1（领导者）领导者是群体中搜索能力最强的，一个群体中只有一个领导者。

定义2（跟随者）跟随者是群体中搜索能力仅次于领导者的一些个体。

定义3（随机者）随机者是群体中搜索能力最弱的一些个体。

2.1.2 群行为

在群体中，领导者代表这个群体最好的搜索方向，它通过自学习来寻找更优的搜索方向；对于跟随者，它们向领导者学习，在领导者周围搜索猎物；随机者是群体中搜捕能力最差的一些个体，它们不向他人学习，常采用基于特征变换的随机游走策略去搜捕领导者和跟随者未搜索过的方向，以期望能发现好的猎物场地。根据上面的描述定义以下三种类型的群行为：

（1）个体自学习；

（2）个体向他人学习；

（3）个体不向他人学习，与他人持反对意见。

同时在群体内和群体间还存在竞争与合作行为。

2.2 竞争模型

在自然界中，群体之间必然存在生存竞争，群体中的个体也是如此。在GCCO 算法中，存在两种竞争，群内竞争和群间竞争。在群体内，能力最差的个体将被淘汰；而在群体间，通常选择一个搜索能力最弱的群体，在其他所有群体之间竞争以拥有这个最弱群体的生产者，而这个最弱群体中的其他个体则被淘汰。通常这两种竞争是同步进行的，如图1所示。

2.3 合作模型

自然界中存在竞争，也存在合作，通过信息共享，群体可发现更优的搜索方向。在GCCO 算法中存在两种合作方式：群内合作和群间合作。

在群体内部，领导者将自己的搜索信息分享给追随者，追随者采用区域复制的方式在领导者周围搜索猎物。在群体间，搜索能力相似的群体通过共享自己最优的搜索方向来实现互利互赢，以勘探出更好的方向搜索，如图2所示。

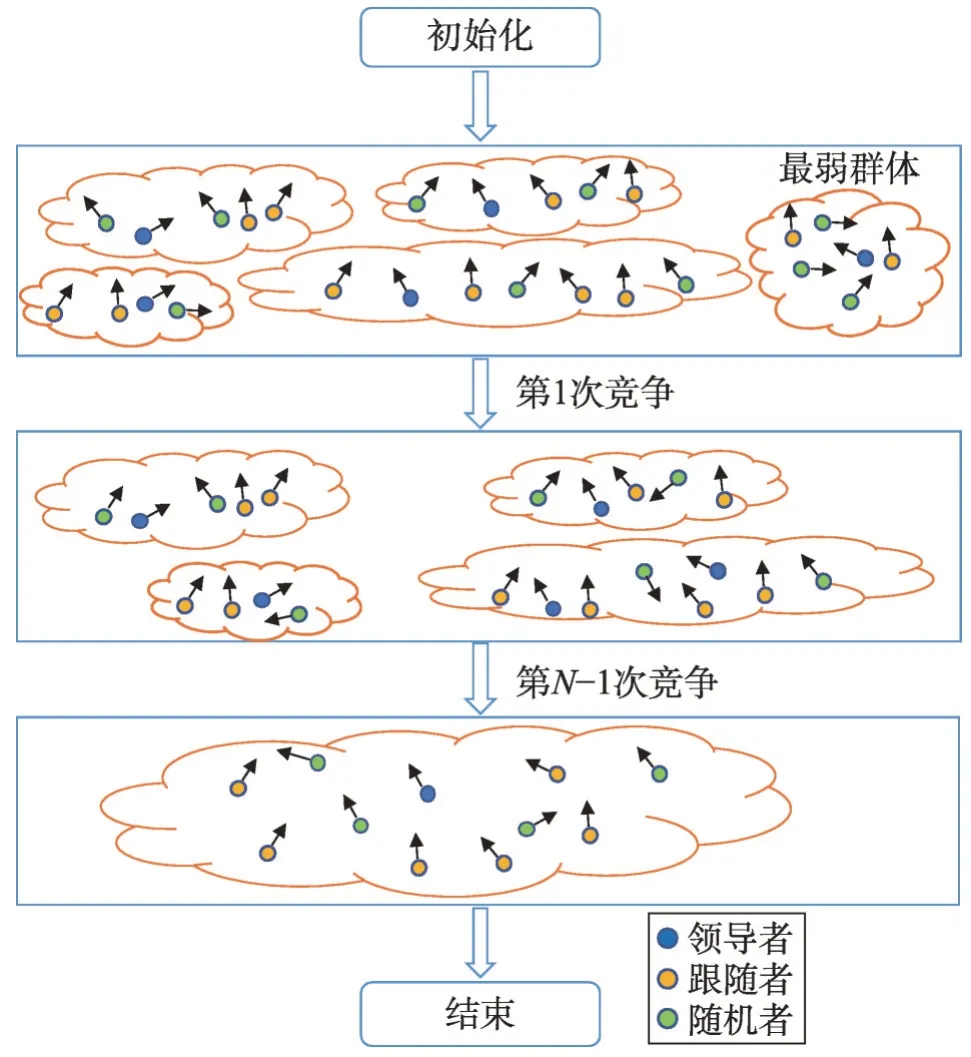
Fig.1 Competition mode图1 竞争模式

Fig.2 Cooperation mode图2 合作模式

2.4 三种模型之间的关系

在GCCO 算法中，初始一个种族分散在N个群体中，每个群体中的n个个体被划分为三个等级：领导者、跟随者以及随机者。在各个群体搜捕猎物的过程中，领导者带领追随者发掘更佳位置，随机者通过特征变换的方式发掘未知位置，且群体内最差个体被淘汰。在群体之间，搜捕能力较强的群体争夺搜捕能力最弱的群体中的领导者，最弱群体中的其余个体被淘汰。同时，能力值相近的群体之间相互合作，共同勘探更优的搜索位置。当这个种族演化到一个群体时，算法结束，这个群体中的领导者就代表了全局最优解。

图3 是GCCO 算法的框架图，由图3 可知深度在GCCO 算法中体现在三方面：第一，算法是深度迭代的，算法通过N-1 次演化，演化成一个群体，每次演化中每个群体内部并行迭代τ次，即算法是通过(N-1)×τ次迭代完成的；第二，随机者采用基于特征变换的方式去搜索未知领域，算法是特征变换的；第三，GCCO 算法中引入了多种模型，算法是具有一定的复杂性的。

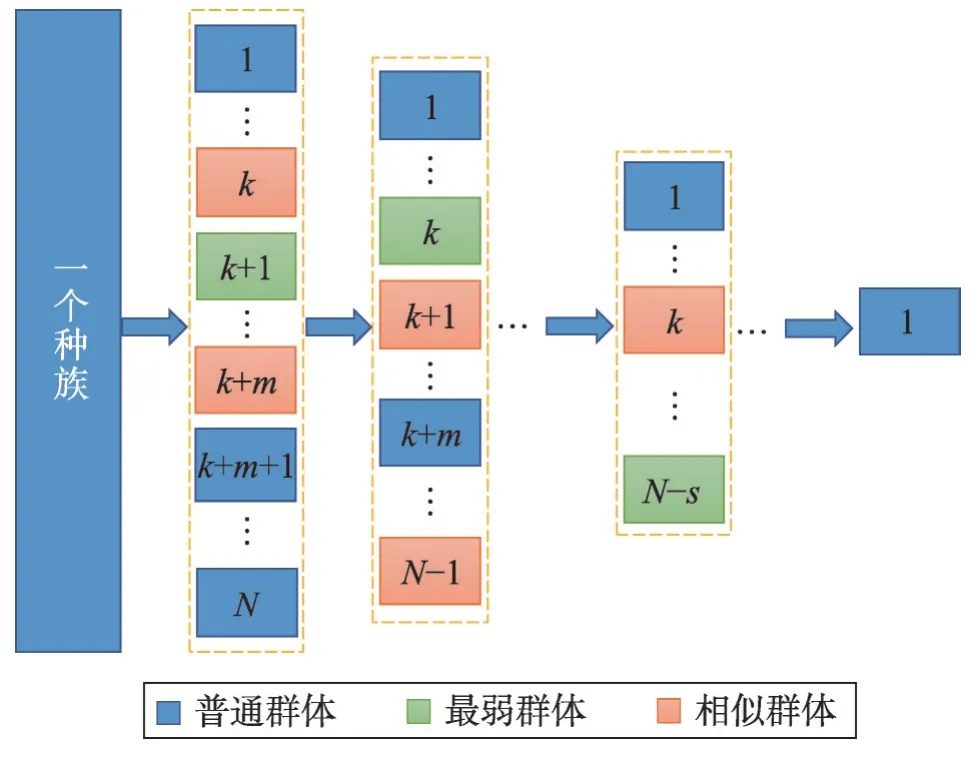
Fig.3 Framework diagram of GCCO algorithm图3 GCCO算法的框架图

3 数学模型和算法

3.1 生物群数学模型

3.1.1 初始化种群

初始化的目的是形成算法初始的一个种族，一个种族有N个群体，每个群体中有三种类型的个体，每一个体存在两种属性，角度θ和方向D。在n维搜索空间中，第k次迭代中的第i个个体的当前位置为为个体的当前头部角度，它的搜索方向是一单位矢量，由式（1）～式（3）计算得出[16-18]。

3.1.2 种群分类

根据适应度值将群体中的个体划分为三类，即领导者、跟随者以及随机者。fit(popi,j)表示第i个群体中第j个个体的搜索能力，第i个群体的种群分类如算法1所示。

定义4（种群分类）对于任意个体gi,j，gi,j∈Ci，Ci={L,F,W}，其中Ci是第i个种群的分类，L、F以及W分别代表领导者、跟随者以及随机者。由生物群模型可知，在第i个种群中，领导者、跟随者以及随机者由式（4）～式（6）分别描述，δ表示搜索能力差值，在实际实验中取适应度值排名前80%的个体为跟随者。

3.1.3 群行为

（1）领导者行为：领导者有自学习能力，它位于最有前途的区域且具有最佳适应值。

定义5（领导者行为）领导者采用扫描定位机制寻找猎物，通过由white crappie 引入的基本扫描策略，将扫描场推广到一个n维空间，其中θmax为最大追踪角，λmax为最大追踪距离。领导者分别向左、向右、向前扫描，在第k次迭代中领导者XL的扫描行为如式（7）～式（9）所示，领导者将从前方(z)、左方（l）以及右方(r)这三点去寻找最佳位置：

其中，c1∼N(0,1)，c2是一个服从0-1均匀分布的n-1维序列。

（2）跟随者行为：跟随者向领导者学习，在领导者附近搜捕猎物。

定义6（跟随者行为）跟随者采用区域复制的方式在领导者附近搜索猎物，通过式（10）更新位置。

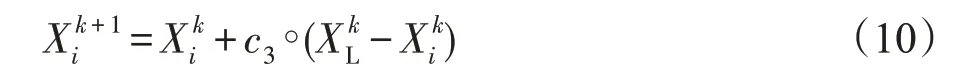
其中，c3是服从0-1均匀分布的n维序列。

（3）随机者行为：随机者不学习，与他人持反对意见。

定义7（随机者行为）随机者采用基于特征变换的随机移动策略，搜索领导者和跟随者未搜索过的区域，即随机者虽自由移动，但采用的移动方向与领导者和跟随者不同，通过式（11）～式（13）更新位置。

算法1群分类模型算法

3.2 竞争数学模型

由竞争模型可知，一个种族中存在两种类型的竞争，群内竞争和群间竞争，且这两种竞争是同时进行的，如算法2所示。

（1）群内竞争：每次演化过程中，每个群体内的个体根据自己的策略去寻找更优的搜捕方向，如果一个个体popi,j的适应度值最差，则popi,j∉Ci。同时，为了保持群体数量稳定，随机生成一个个体加入到群体中。

（2）群间竞争：群体之间通过竞争，淘汰一些弱势群体，最终只有强者才能生存下来。

定义8（群间竞争）对于每一群体，abilityi表示第i个群体的综合实力，则对于第i个群体，它的综合实力由式（14）定义，其中ξ=0.1，再用式（15）正规化第i个群体的综合实力值。

则群体i的占有率，对于N个群体则有向量P=[P1,P2,…,PN]。对应创建一个与P同样大小的向量Q，则Q=[Q1,Q2,…,QN]，其中Q1,Q2,…,QN～U(0,1)，则有：

根据D向量，将最弱的群体中的领导者给D中概率最大的群体，最弱的群体消失，在演化最后，只剩下一个群体。

算法2竞争模型算法

3.3 合作数学模型

根据前面的合作模型可知，合作的形式有群内合作和群间合作，如算法3所示。

（1）群内合作：跟随者的位置更新就是群内合作，跟随者通过领导者分享的角度、位置信息来进行搜捕猎物，从而跳出自己搜索的局部最优。

（2）群间合作：相似群体向对方学习，以发掘出更优的搜索方向。

定义9（相似群体）在N个群体中，如果有群体Si和Sj满足|abilityi-abilityj|=min|abilityi-abilityj|，其中i,j=1,2,…,N，则Si∼Sj。

定义10（群间合作）相似群体中的跟随者向对方的领导者学习以了解对方的最优搜索区域，相互合作，共同寻找更优的搜索空间，则对于第i个群体中的跟随者，它像第j个群体中的领导者学习，位置更新公式如式（16）和式（17）所示，反之亦然。

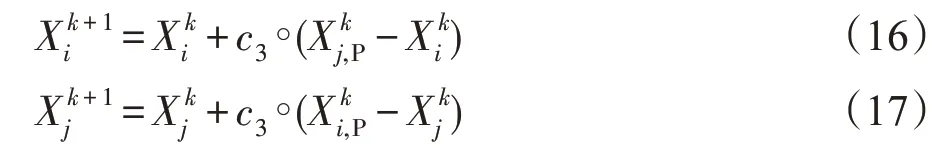
算法3合作模型算法

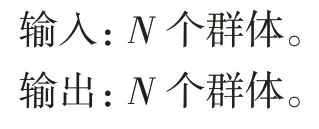
3.4 变步长数学模型

跟随者采用固定步长的区域进行搜索，若在较大步长的复制区域内移动，则算法收敛速度较快，但在接近全局最优解时，会因步长过大而在峰值附近振荡，出现精度低的问题；若采用较小的步长，算法优化精度会提高，但是收敛速度太慢且易陷入局部最优[19]。

通过分析步长对算法性能的影响，在算法前期，采用较大的步长来加快算法收敛；在算法后期，采用较小的步长来尽可能逼近极值。结合迭代次数，为步长引入一个权值，如式（18）所示，其中t为当前迭代次数，T为总迭代次数，则跟随者的移动策略如式（19）所示。

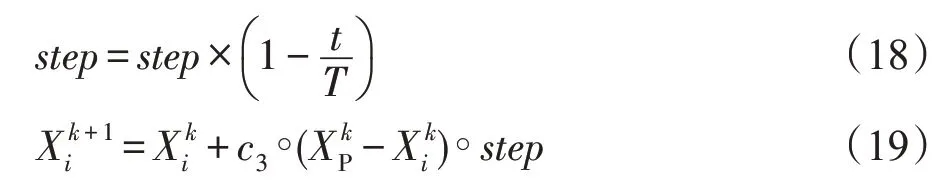
3.5 GCCO算法

算法4GCCO算法

4 GCCO算法的理论证明

在GCCO算法中，一个种族被划分为N个群体，由于存在群体间的竞争，种族每经历一次演化，都有一个群体被淘汰，直到最后只有一个群体存活了下来。由于每个群体有相同的演化策略，将其定义为E，若E是收敛的，则整个算法就是收敛的。

对于任意一个优化问题＜A,g＞和随机优化算法E，算法在第t次迭代的结果是Xt，则算法下一次迭代的结果Xt+1=E(Xt,ς)，其中ς表示由算法E找到的解。

假设1如果g(E(x,ς))≤g(x)，则有g(E(x,ς))≤g(ς)。

假设2假定在第t次迭代后的解Xt不是最优的解，那么算法在第(t+1)次得到一个更优的解的概率是Pt+1∈(0,1)。

理论1如果一个算法满足假设1 和假设2，那么这个算法是收敛的。

证明由假设2 可知，算法能够获得比当前更好的解的概率是，那么有。由假设1 可知，优化算法的适应度值是非递增的，由优化算法所产生的值总是不差于目前的个体。结合假设1和假设2可知，算法总是能找到更好的解直到它收敛，因而可以证明算法是收敛的。 □

理论2算法E满足假设1。

证明无论是否存在竞争和合作行为，算法E中的领导者都是最优的个体，这是由领导者的定义而来的。领导者通过自学习，将扫描的三个点与当前的位置比较来选择最佳的搜捕方向，因此有g(Xl,t)≤g(Xl,t-1)，即g(E(X,ς))≤g(X)。且在这次迭代之后，选出最优的粒子作为领导者，即。领导者的值是在这次迭代中值最小的粒子，因此也满足g(E(X,ς))≤g(ς)，故算法E满足假设1。 □

引理如果解空间S是有界的，并且适应度函数在S上是连续的，那么算法E满足假设2。

证明通常解空间可以分为两部分：一是最优点X*的邻域部分，用S1表示；另一部分用S2表示，且S2=S-S1。则当前解可以划分为两种情况：一是至少有一个解在S1内；二是所有的解都在S2内。

如果当前第t次迭代的解属于第一种情况，则由理论2 可知，在接下来迭代过程中，至少有一个解在S1中。这种情况同时满足假设1和假设2，则由理论1可知，算法E最终收敛到最优解。

如果当前第t次迭代的解属于第二种情况，由于g(xt)在S上是连续的，将Xm满足||Xm-Xl||∞≤∂和|g(Xm)-g(Xl)|＜ε(ε＞0)的集合记为M，则M⊂S1。且有：

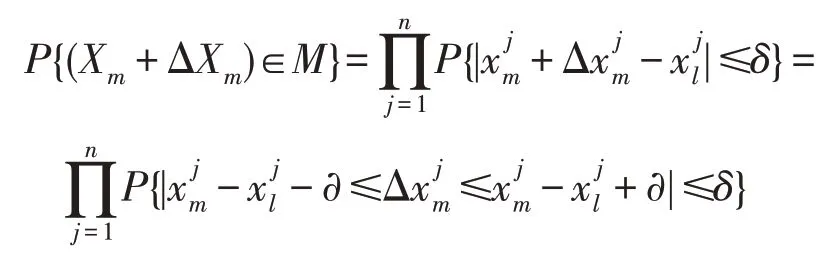
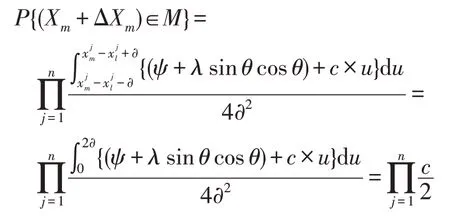
从中可知，当0＜c＜2 时，0＜P{(Xm+ΔXm)∈M}＜1，这意味着这个点属于M的概率是（0，1）。则在假设1的情况下可证明算法E满足假设2。 □

理论3算法E有一个有界的解空间S，当适应度函数在S上是连续的，则它是全局收敛的。

证明由假设1 可知算法E是满足假设2 的，则根据理论2，算法E是收敛的。但前提是适应度函数在有界的解空间内连续。 □

5 实验和分析

这部分主要是对所提深度演化算法（GCCO）性能的分析，首先在十个优化函数上与帝国竞争算法（imperialist competitive algorithm，ICA）、社会蜘蛛算法（SSO）以及群搜索算法（group search optimizer，GSO）这三种算法比较，其次在提高上海市燃气事故到场及时率问题中测试GCCO算法解决实际问题的能力。

5.1 优化函数测试

这里采用的十个优化函数是文献[5]中的部分函数，函数描述与文献[5]中一致，实验通过与GSO、ICA 以及SSO 这三种算法对比来验证GCCO 算法的性能。在实验中，算法的最大迭代次数均为1 000(τ=1 000)，初始种群大小为50(n=50)。每个算法的参数设置如表1所示。

表2 是GCCO 算法和其他三种算法在30 维的优化函数上的对比结果，表中加粗的字体表示函数值较低，实验运行50次，在平均值和标准差这两个指标上验证算法性能。实验结果表明GCCO算法只有在Rastrigin函数和Rosenbrock函数上的std指标性能不太理想，在其他函数上均有最优性能。且从图4中可直观看出，GCCO 算法在所有函数中均能寻得最优值，尤其在Salomon 函数和Sum-of-square 函数中，GCCO算法在前几百次的迭代中就能寻得最优值0。

Table 1 Parameter settings for four algorithms表1 四个算法的参数设置

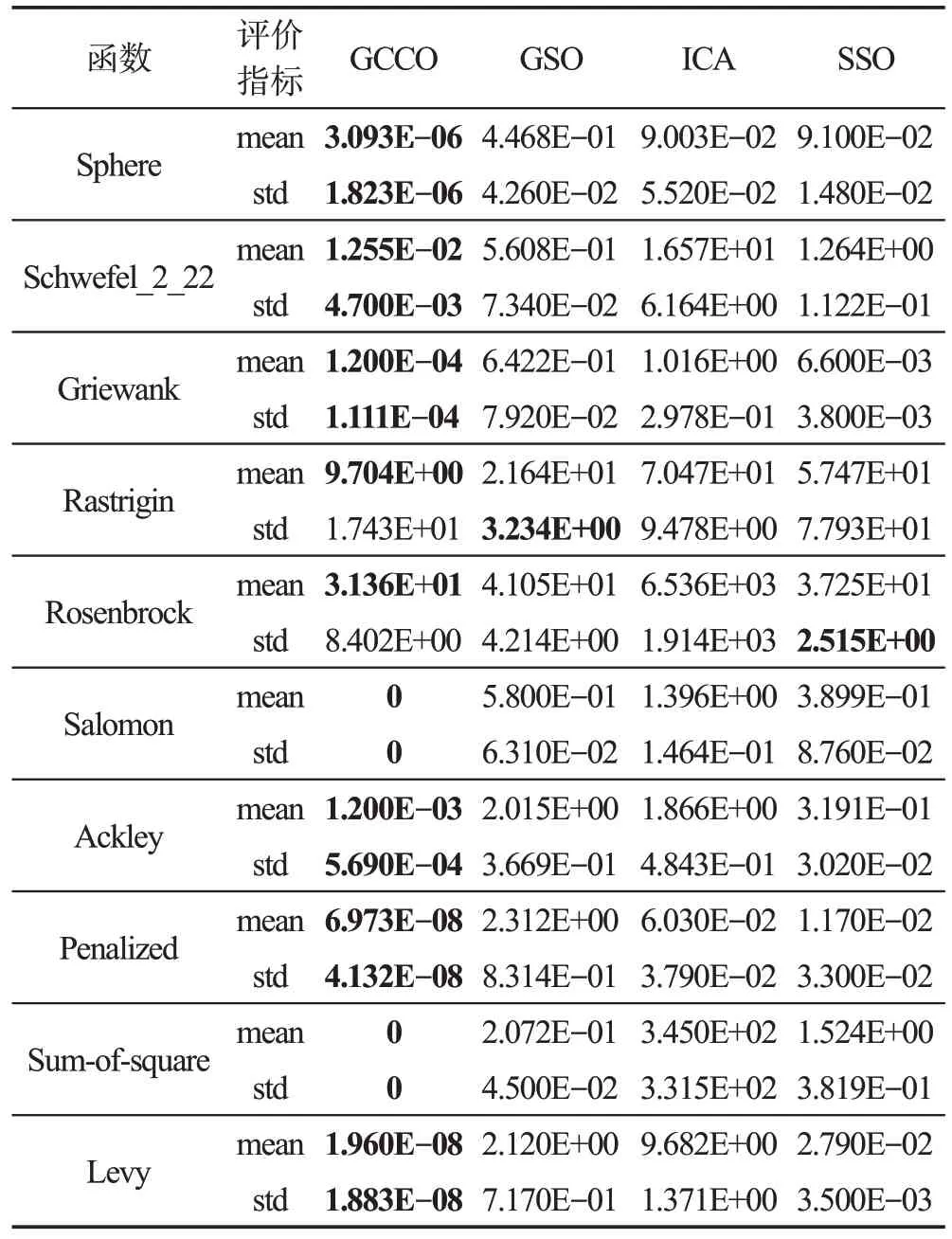
Table 2 Comparative experimental results on 30-dimensional optimization function表2 30维的优化函数上的对比实验结果

Fig.4 Experimental results of GCCO algorithm and three other algorithms in 30 dimensions图4 GCCO算法和其他三种算法在30维上的实验结果图

为了测试GCCO 算法解决高维问题的性能，分别在50维和100维的优化函数上对算法进行了测试，表3和表4是实验结果，表中加粗的字体表示函数值较低。从表3 可以看出，在50 维优化问题中，GCCO算法只有在Griewank 函数中的性能仅次于SSO 算法，在其他函数均有最佳性能。在表4 中，GCCO 算法在100 维的Griewank 函数和Ackley 函数中的性能仅次于SSO算法，且在Penalized函数中的mean指标性能较差，在其他函数上也均有最佳性能。故可以看出在解决高维问题上，GCCO算法也有较好的性能。

Table 3 Comparative experimental results on 50-dimensional optimization function表3 在50维的优化函数上的对比实验结果

为了更进一步分析算法的有效性，使用Wilcoxon测试和Friedman测试这两个非参数统计技术来分析GCCO算法在30维连续优化问题上所获得结果的性能[20-21]。Wilcoxon 测试的结果如表5 所示，Friedman测试的结果如图5 所示。从表5 可以看出，除了SSO算法，其他算法的P值均小于0.05[21]，且6.457E-02也是很小的一个值，故GCCO 算法性能是优于其他三种算法的。图5是秩和检验分析，显示了各个算法的排名，值越小说明该算法越优，从中可以看出，在十个函数中GCCO算法均有最小排名。

Table 4 Comparative experimental results on 100-dimensional optimization function表4 在100维的优化函数上的对比实验结果

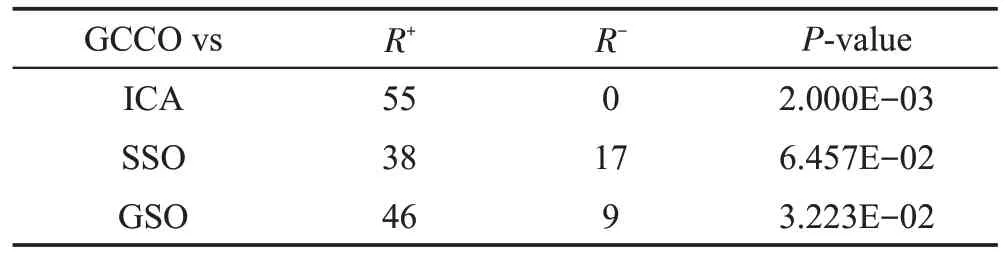
Table 5 Wilcoxon test results on ten 30-dimensional optimization functions表5 在十个30维优化函数上的Wilcoxon测试结果

5.2 实际应用

在解决上海市燃气事故到场及时率问题中，需对12 619 条燃气数据进行数据预处理，先对上海市燃气事故所在区域划分栅格，再对事故时间段划分时间片，将数据处理成一个行为栅格编号列为时间片编号的二维矩阵。

5.2.1 数据预处理

定义11（栅格）将空间分割成大小一致的网格，一个网格即为一个栅格，这里根据事故的墨卡托坐标将上海市划分成a×a的栅格（单位m），得到每个栅格的编号(x,y)，共计b个栅格。其中x∈[c,d]，y∈[e,f]。

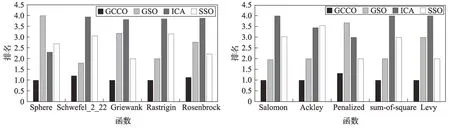
Fig.5 Friedman test on ten 30-dimensional optimization functions图5 在十个30维基准函数上的Friedman测试

定义12（时间片）将燃气事故数据始末时间段划分为时间间隙为g小时的h等份，其中每一份即为一个时间片。

基于定义11 和定义12，则任意栅格在任意时间片内都有相应的状态属性state，这样完成了对数据的预处理，将数据表示成了b×h的一个二维矩阵Matrix。

在实际上海市燃气事故到场及时率问题中，state的值如下所示，负数值越小表示相应的事故优先级越低，事故时间段为2016 年9 月4 日—2018 年11 月26 日，且a=256，b=7 140，c=52 000，d=54 000，e=14 000，f=15 000，g=4，h=4 878。

5.2.2 目标函数定义

在GCCO算法中，每个群体初始化50个粒子，每个粒子有两个维度，分别代表栅格的x坐标和y坐标，则每当粒子Z移动到一个位置时，粒子Z的适应度值就等于在这个位置设立一个站点后的上海市未及时率。设立一个站点后的未及时率的计算为：粒子Z按列遍历矩阵Matrix（即按时间片遍历每个时间片内的栅格），按优先级查看未及时到达事故，计算站点（粒子）到对应栅格的时间T（T=），若一个优先级有多起事故且能在30 min内到达的处理距离最近的事故，否则转看下一个优先级的事故，且每个时间片只能处理一个未及时到达事故，将其负的状态值改为1。将这个过程定义为ACT，令ACT(z)为设立站点z后未及时到达的事故数。用SUM表示总事故数，则未及时率unarriverate=，通过粒子演化，找出未及时率最低的粒子，即最优站点的位置。

5.2.3 实验结果

在这部分，加入全局搜索（global search）的实验结果，即对所有栅格（1 000×2 000个栅格）进行遍历，算出所有栅格分别设立站点后的未及时率，求出未及时率最多能降低到35.681%，这是最优的一个结果。

在算法参数设置中，和上面优化函数设置相同，将GCCO 算法与ICA、SSO、GSO 算法以及global search 进行对比，算法运行50 次。由表6 可知，在解决大数据量的实际问题中，GCCO 算法是明显优于ICA 算法的，GCCO 算法将未及时率从初始48.819%降低到了35.841%，虽然GCCO 算法比SSO 算法（降到了36.360%）和GSO算法（降到了36.408%）只分别多优化了0.52个百分点和0.57个百分点左右，但在实际设立站点问题中，未及时率最多能降低到35.681%，一个站点的设立只能顾及方圆15 km的区域，多优化0.52 个百分点和0.57 个百分点能体现出GCCO 算法的性能是比GSO算法和SSO算法优越的。且GCCO算法与全局搜索相比只差了0.16 个百分点，但所花费的时间确是远远少于全局搜索的时间的，花费少量的时间却能获得较好的效果这是所需要的。从图6可直观地看出，GCCO 算法收敛速度较快，且能寻得最优值，这些都证明了将深度引入演化算法来解决实际问题的有效性。

Table 6 Performance comparison of five algorithms on reducing untimely rate problem表6 五种算法在降低未及时率问题上的性能对比

Fig.6 Experimental comparison of four algorithms图6 四种算法实验对比

6 总结与展望

本文将深度引入演化算法中，提出一种基于群竞争合作行为的深度演化算法（GCCO算法），算法通过多步迭代可以实现极值问题的求解。在算法中引入竞争模型和合作模型提高算法的性能，在跟随者移动过程中，采用变步长策略，均衡了算法精度和收敛速度问题。在随机者移动过程中，采用基于特征变换的游走方式，避免算法陷入局部最优。将所提深度算法在十个基准函数上进行了测试，并分别在30维、50维以及100维上检测算法的性能，实验结果表明，相对于ICA、SSO以及GSO算法，GCCO算法表现出良好的性能，并使用非参数统计技术Wilcoxon测试和Friedman测试来分析GCCO算法在30维连续优化问题中的性能。最后为了验证算法在解决实际问题上的有效性，将算法用于12 619 条上海市燃气事故数据中，找出合适的位置来设立站点降低上海市事故未及时率。实验结果也验证了GCCO算法解决大数据量的实际问题的能力，但是本文所提出的深度演化算法还只在初级阶段，今后还需对深度与演化算法进行更深入复杂的研究。