大豆水分含量测量的不确定度评定

杨永隆　梁静

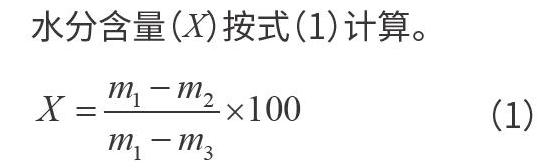
摘 要：通过105℃直接干燥法对大豆进行水分含量的测定，并建立相应的数学模型，分析不确定度来源，依照不确定度分类，对不确定度分量、合成标准不确定度和扩展不确定进行计算和评定，最后得到大豆水分的扩展不确定度。本实验结果表明：大豆水分含量测定时恒重是减少误差的关键步骤。

关键词：大豆;水分含量;不确定度

大豆是全球食物原料的重要组成部分，可以加工制成豆腐、豆乳、豆粉等豆制成品，并且从大豆中提取食用油后所剩副产品豆粕，更是商品猪和家禽饲料的来源，因此大豆价格上涨会向下游产品肉类、油脂价格传递，影响国内养殖、粮食及油脂生产等生产成本的提高，其中大豆价格差异与其质量品质相关。大豆中的水分含量会关系到其品质好坏，最终影响大豆质量，并直接影响其收储、运输、加工等，因此需对水分进行科学准确的检测。本文依据GB 5009.3-2016《食品安全国家标准 食品中水分的测定》[1]的直接干燥法和JJF 1059.1-2012《测量不确定度评定与表示》[2]的技术规范要求，评定大豆水分含量测定结果的不确定度。

1 大豆水分含量的测量方法和测量的数学模型

1.1 检测设备

称量瓶（铝制带盖）：内径4.5 cm、高2.0 cm;干燥器（内含有效干燥剂）;精密烘箱：型号美国赛默飞世尔OMS100;万分之一天平：型号瑞士梅特勒-托利多AB204-S/A。

1.2 测定步骤

将洁净称量瓶放置（103±2）℃精密烘箱内烘1 h，取出置于干燥器中冷却至室温，取出称量。再重复干燥直至恒重（即两次称量之差小于2 mg）;平均分取样品约30 g，去除样品中的矿物质和杂质，粉碎，细度小于2 mm，混匀;称取3 g试样，放入称量瓶中，平铺开，厚度不超过0.5 cm;置于（103±2）℃精密烘箱内，盖子斜支盒边，烘3 h后，盖好取出，放入干燥器冷却至室温称量，然后再放入（103±2）℃精密烘箱内烘1 h左右，取出，放入干燥器冷却至室温后，再称量直至恒重[3]。

1.3 数学模型

水分含量（X）按式（1）计算。

（1）

式（1）中：X—样品中水分的含量，单位为克每百克（g/100 g）;m1—称量瓶和试样的质量，单位为克（g）;m2—称量瓶和试样烘后的质量，单位为克（g）;m3—称量瓶的质量，单位为克（g）。

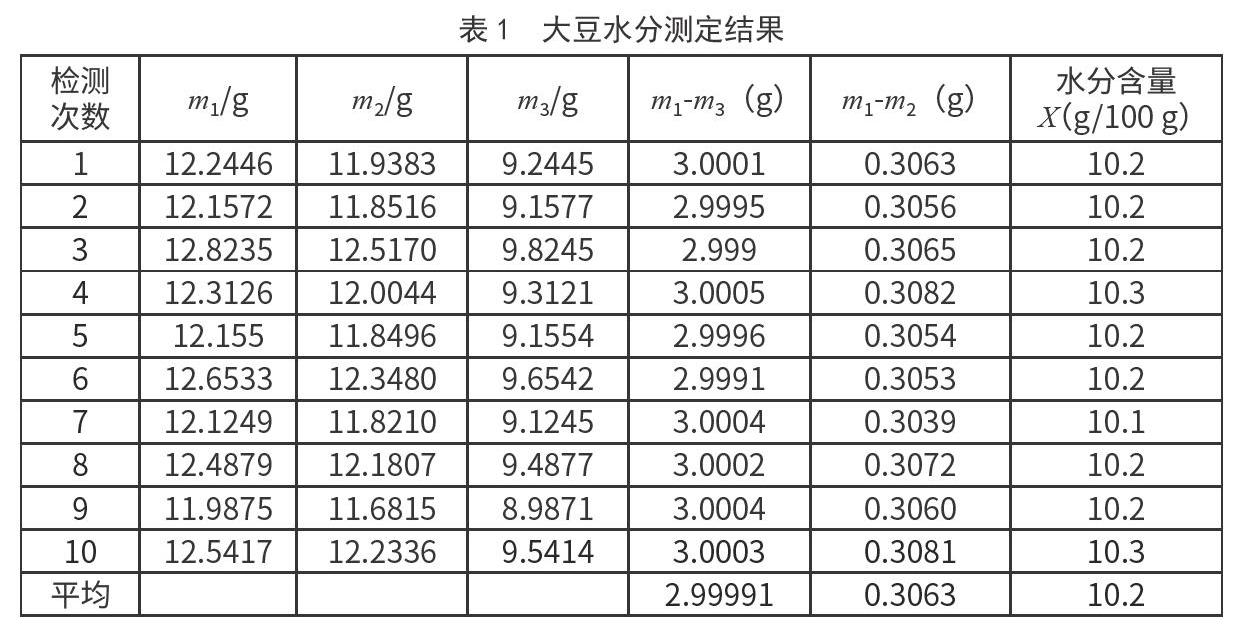
1.4 测定结果

测定结果见表1。

2 不确定度评定

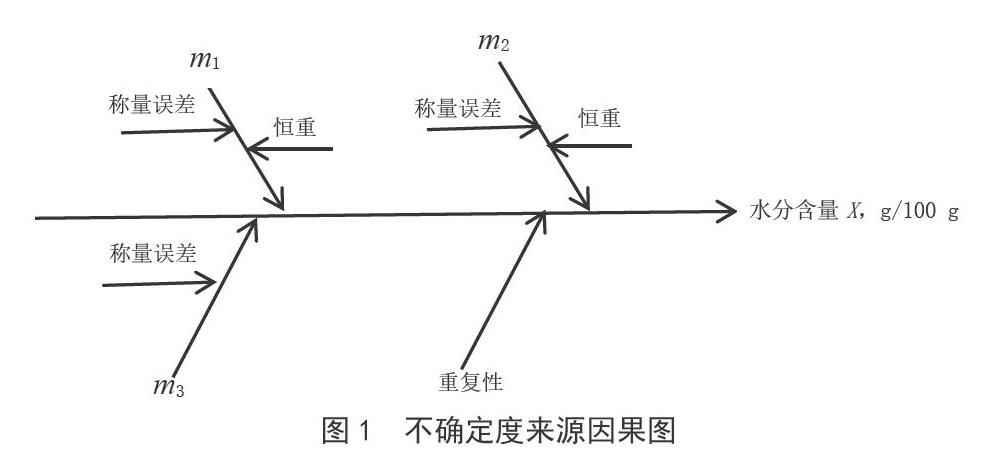
2.1 不确定度来源分析

温度、湿度等实验环境均满足标准规定，因此可忽略该不确定度来源，从测量程序可得，大豆水分测量过程中引入不确定度的分量如图1所示[3]。

2.2 重复性测定引入的标准不确定度

A类标准不确定体现在重复性中，来源包含样品均匀性、测定时的随机效应和称量变动性等。按照A类评定方法，重复性引入的不确定度us（A），可由独立重复观测得到一系列被测量值，带入贝塞尔公式进行评定。

因此，在相同测量程序和条件下，A类标准不确定度的评定可用统计学的分析方法，按式（2）进行评定。

（2）

式（2）中：Sx——实验标准偏差;n—重复实验次数。

因此重复测量引入的标准不确定度为：

2.3 B类标准不确定度

B类标准不确定度来源于天平校准（分辨率和最大允许误差MPE引入的不确定度）和恒重（称量干燥前后的称量瓶质量和干燥后试样的质量引入的不确定度）这两方面，需使用非统计分析的方法进行相关评定。

2.3.1 天平称量引入的标准不确定度ucl（m）

天平分辨率引入的标准不确定度，因实验用的电子天平的参数d=0.1 mg;e=1 mg;MAX=220 g，由矩形分布，可得分辨率引起的标准不确定度Ud（m）为：

天平最大允许误差（MPE）引入的标准不确定度：根据天平检定报告，实验用的天平准度等级为Ⅰ级，且当0

因此电子天平称量存在的合成不确定度为：

2.3.2 恒重判断行为存在的标准不确定度uh（m）

测定程序中称量瓶和试样烘及恒重的标准。（103±2）℃精密烘箱复烘1 h，冷却至室温再称量，直至2次称量差小于2 mg。

假设该判断方法带来的误差服从矩形分布，则恒重引入的标准不确定度：

2.3.3 称量瓶质量m3引入的标准不确定度u（m3）

称量瓶质量m3主要受天平称量误差和恒重这两方面的影响，称量中的变动性已纳入重复性考虑，又因天平校准和恒重是独立的两个分量，因此称量瓶质量m3的合成不确定度为：

2.3.4 称量瓶和试样的质量m2引入的标准不确定度u（m2）

因将称量中的变动性纳入重复性，且质量m2不受恒重的影响，所以只考虑天平使用引入的标准不确定度，因此称量瓶和试样的质量m2引入的标准不确定度为：

u（m2）=ucl（m）=0.00013 g

2.3.5 称量瓶和试样干燥后的质量m1引入的标准不确定度u（m1）

与称量瓶质量m3相似，质量m1主要考虑受天平称量误差和恒重方法的误差的影响，因此称量瓶和试样干燥后的质量m1引入的标准不确定度为：

2.4 水分合成標准不确定度的计算

在计算公式中各分量不相关，设a=m1-m3，b=m1-m2，则式（1）中数学模型改写为

又m1、m2、m3是独立测量所得，所以

因此其合成标准不确定度为：

2.5 大豆水分测定的合成标准不确定度uls（X）

本次测定评定中A类标准不确定度）和B类标准不确定度）是相互独立互不相关的，水分测定结果的合成标准不确定度是两者一起贡献的结果，因此大豆水分的合成标准不确定度为：

3 扩展不确定度U和大豆水分测量不确定报告结果

取包含因子k=2，且P=95%的测量可能值置信概率下，大豆水分的扩展不确定度为：

u=2×u1s=2×0.000 431

=0.000 862

所以，本文大豆样品水分含量最终结果可以表示为：

X=（10.2±0.1）%，k=2，P=95%。

4 结论

从大豆水分含量的测定程序不难看出，在人员、温湿度和方法基本不变的条件下，影响大豆水分测定结果变化的主要因素为恒重引入的不确定分量（称量瓶的质量、称量瓶和试样烘后的质量），即大豆水分含量测定时恒重是减少误差的关键步骤，因此，在试验过程中，严格执行烘至恒重的要求能有效降低B类不确定度，从而降低最终结果的扩展不确定度。

参考文献

[1]GB 5009.3-2016 食品安全国家标准食品中水分的测定[S].北京：中国标准出版社，2016.

[2]JJF 1059.1-2012 测量不确定度评定与表示[S].北京：中国质检出版社，2012.

[3]黄永东，李博，李洪程.大米水分测量结果不确定度的评定[J].粮食储藏，2008，37（1）：40-42，46.