考虑磁致伸缩效应的永磁同步电机磁-机械耦合模型
2020-07-09于慎波窦汝桐夏鹏澎
夏 林,于慎波,窦汝桐,夏鹏澎
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引 言
为了使电机满足某些特殊应用场合的要求,尤其在军工和家用电器领域,对电机的振动噪声指标的要求近乎苛刻,越来越多的学者研究电机的振动噪声问题。电机振动噪声的来源主要有机械噪声、空气噪声和电磁噪声三个方面,目前普遍认为电磁力是电机电磁振动噪声的主要激励源,但忽略了磁致伸缩效应的影响[1-2]。磁致伸缩效应是铁磁材料的固有属性,且对外部应力变化特别敏感,磁致伸缩是指铁磁材料在磁化状态下会沿着磁场方向发生伸长或缩短,这个应变不同于其他由机械或电磁应力而产生的应变[3]。在低频条件下,在船舶潜艇等军用装备中,磁致伸缩效应可能会显著加剧振动噪声幅值。
2002年,美国佛罗里达州大学的Mohammed教授建立了考虑磁致伸缩效应的电机定子铁心的磁-弹性模型,通过数值计算分别得出了考虑磁致伸缩效应和电磁力单独作用时电机定子铁心齿部所受应力,在考虑磁致伸缩效应时,齿部应力与电磁力单独作用相比增加了50%[5-6]。2009年,英国Sakda Somkun教授与其学生对考虑磁致伸缩效应各向异性情况下的电机定子铁心的振动变形进行了研究,与普通计算结果相比,考虑磁致伸缩各向异性时的计算结果更加接近电机实际工作情况,有效地提高了电机仿真计算的精确程度[7]。
近年来,国内对于磁致伸缩效应研究也不断增加。文献[1]研究了磁致伸缩效应对变压器振动噪声的影响,建立了变压器铁心磁-机械耦合模型,研究结果表明,磁致伸缩效应时的振动噪声结果比实际工作情况误差更小。沈阳工业大学张艳丽教授及其研究团队对旋转磁化条件下、直流偏磁条件下和谐波磁场下的硅钢片磁致伸缩特性进行了研究[8]。文献[9-10]研究了变频器供电条件下永磁电机的振动噪声问题,实验结果表明,随着供电电流频率的提高,电机振动噪声也会随之增大。文献[11]通过线性压磁方程来建立考虑磁致伸缩效应的解析计算模型。
1 建立数学模型
1.1 定子磁场分析
根据麦克斯韦方程,建立电机定子铁心磁场模型:
×H=J
(1)
(2)
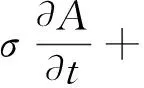
(3)
B=×A
(4)
式中:H为磁场强度;e为电场强度;B为磁通密度;σ为电导率;A为磁矢量势;J为外部电流密度。
1.2 磁致伸缩力的计算
在计算磁致伸缩力的过程中,假设定子铁心材料变形均匀且完全服从胡克定律,则磁致伸缩应力:
Fms=G·P
(5)
式中:G为弹性矩阵;P为磁致伸缩应变。
假设材料呈现各向同性,弹性矩阵G可由材料的弹性模量和泊松比表示,对于二维平面应变问题,则有:
(6)
式中:E为材料的弹性模量;α为材料的泊松比。
磁致伸缩应变P通过磁通密度B向定子铁心材料的B-P磁致伸缩特性曲线插值得到,材料的磁致伸缩特性曲线如图1所示。
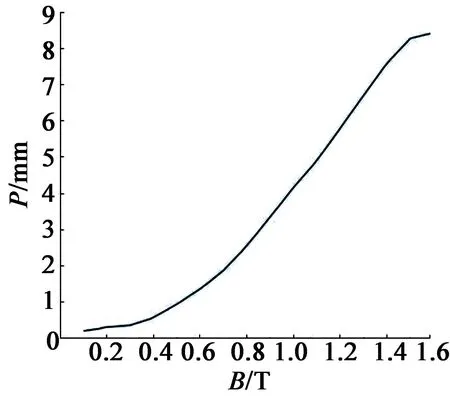
图1 硅钢片磁致伸缩特性曲线
1.3 耦合模型的建立
永磁同步电机系统的总能量W由弹性能U1和磁场能U2两部分组成:
(7)
式中:u为定子振动位移;K为机械刚度矩阵;A为磁矢量势;M为磁场刚度矩阵。
由于能量项的类似形式,采用式(7)的方程组来表示耦合的磁-机械系统:
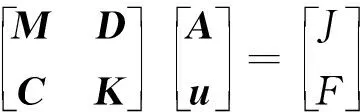
(8)
式中:F表示与电磁无关的外部力;C,D表示耦合项,耦合项C表示磁场对于机械振动位移的作用,耦合项D表示定子振动位移对磁场的影响。
为了简化磁机械耦合系统,用机械系统总能量分别对振动位移u、磁矢量势u求偏导,则有:
(9)
结合式(8)和式(9)可得:
(10)
用弹性能U1对磁矢量势A求偏导,且用磁场能U2对定子振动位移u求偏导,则有:
(11)
由于在小型电机中忽略了电机尺寸的微小形变对磁场分布的影响,所以采用弱耦合的方式,即耦合项D为0;耦合项C表示磁场对于机械振动位移的影响,所以C右乘磁矢量势A即可得电磁力:
Fmag=-CA
(12)
因此磁-机械耦合系统转变:
(13)
现在,在分析工程中用磁致伸缩力Fms来表示磁致伸缩效应,磁致伸缩力可以直接加到外部力F和电磁力Fmag上[12],则考虑定子铁心硅钢片磁致伸缩效应的耦合模型:
(14)
2 定子铁心有限元分析
本文的研究是将磁-机械耦合问题看作是弱耦合问题,在弱耦合问求解中,先计算单元的电磁力、磁致伸缩力和机械应力,再通过这些来计算定子齿部的振动位移[13-14]。
本文的永磁同步电机模型为8极36槽的表贴式永磁电机,通过有限元仿真软件建立定子铁心磁-机械耦合模型,并对电机振动噪声进行仿真研究。电机在工作过程中的主要工作参数如表1所示。由于永磁同步电机的均匀对称性,为了方便对其进行仿真分析,减少计算机的工作量,提高计算效率,本文采用二维平面模型对其进行仿真计算分析。二维平面模型图和计算参考点如图2所示。

表1 电机主要参数

图2 电机二维模型图
在有限元仿真过程中:首先通过ANSYS Maxwell对电机二维模型进行电磁场仿真,得到如图3所示的电机磁通密度分布云图和定子齿尖电磁力等相关数据;其次,在MATLAB中根据得到的磁通密度B向硅钢片磁致伸缩特性曲线插值计算得到磁致伸缩应变、磁致伸缩力等数据;最后将电机定子的三维模型导入ANSYS Workbench中,分别对电磁力单独作用时、考虑磁致伸缩效应时电机定子的振动噪声响应进行仿真。
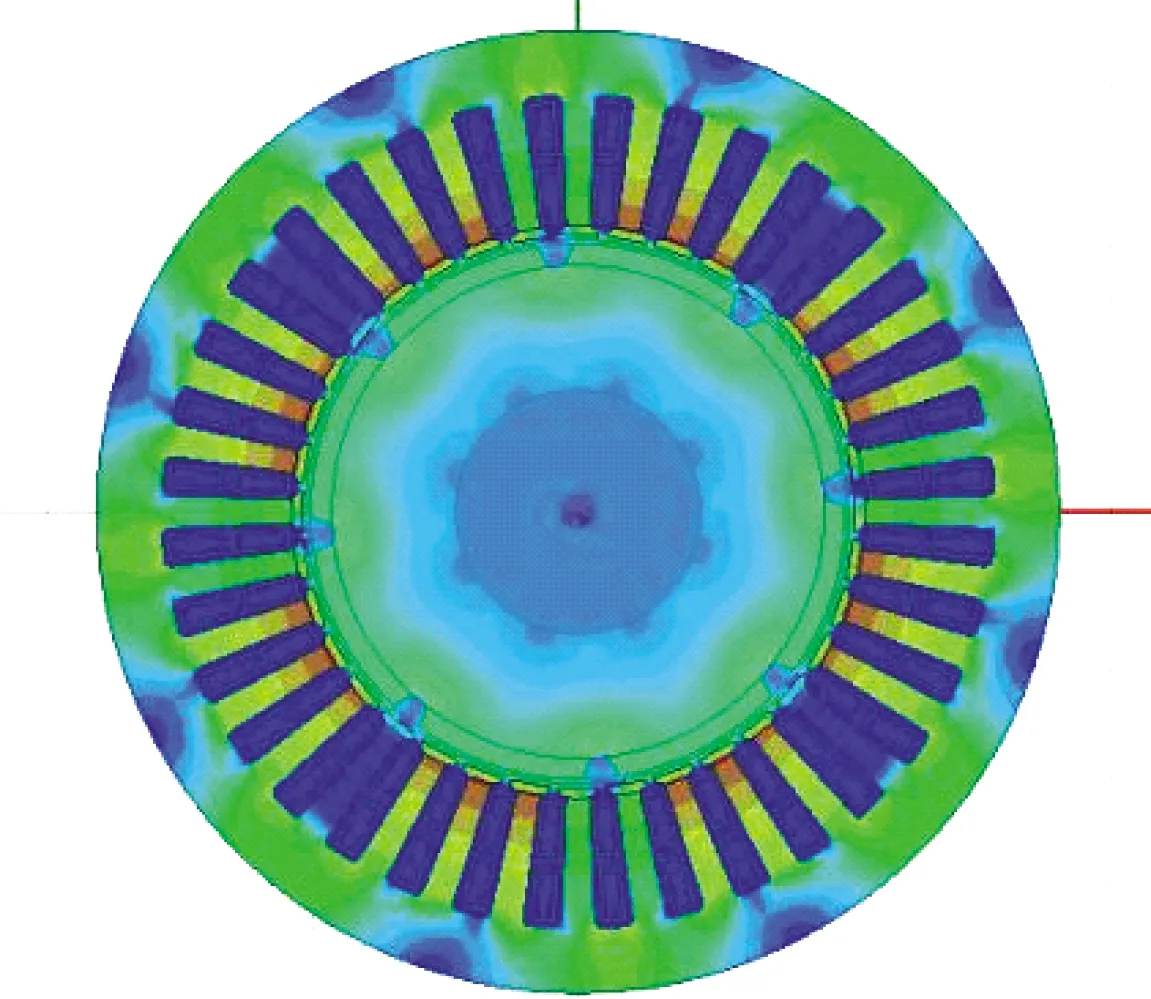
图3 永磁电机磁通密度分布云图
将Maxwell计算出的径向磁通密度数据导出到MATLAB中,然后根据图1的磁致伸缩特性曲线插值得到定子铁心的磁致伸缩应变,并结合式(5)计算考虑磁致伸缩效应而产生的磁致伸缩力,如图4所示。图5和表2展示了考虑磁致伸缩效应时和电磁力单独作用时的定子齿径向电磁力密度,为了方便观察,取半个电周期的数据作为参考。
由图4、图5和表2可以看出,磁致伸缩效应对定子铁心的振动噪声确实存在不可忽略的影响,在磁致伸缩效应作用下,定子齿径向力密度的幅值增加了13.1%,平均值增加了25%。

图4 定子齿径向磁致伸缩力密度图

图5 定子齿径向力密度图
表2 径向电磁力密度参数
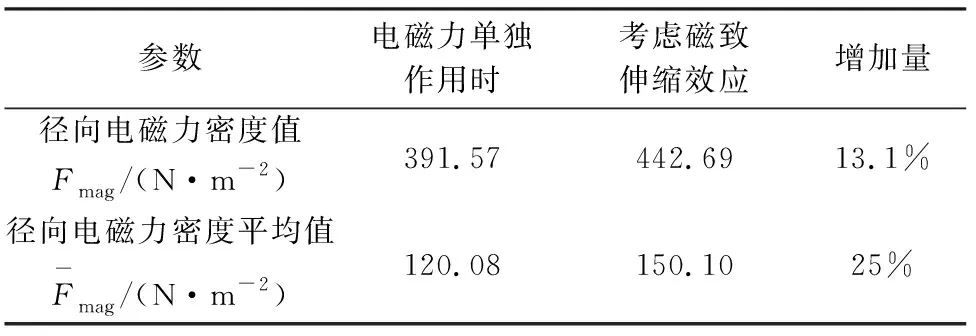
参数电磁力单独作用时考虑磁致伸缩效应增加量径向电磁力密度值Fmag/(N·m-2)391.57442.6913.1%径向电磁力密度平均值F-mag/(N·m-2)120.08150.1025%
将图5两种情况下的径向力密度数据依次作为外加载荷在ANSYS Workbench中加到定子齿表面,以进行磁-机械耦合的谐响应计算。图6(a)和图6(b)分别给出了单独考虑电磁力和考虑磁致伸缩效应作用下定子铁心表面应变分布情况,为了强化视觉效果,缩放比例为106。

(a) 电磁力单独作用
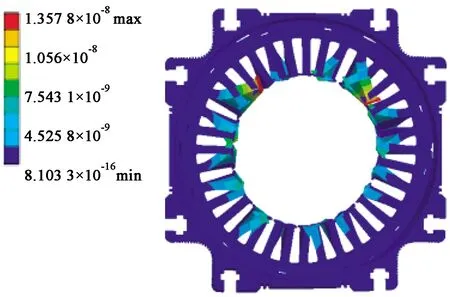
(b) 考虑磁致伸缩效应
对比图6(a)和图6(b)可以发现,在考虑磁致伸缩效应时,定子铁心的变形量均比电磁力单独作用有所增加,齿部的最大变形比电磁力单独作用时增加了13.4%,说明磁致伸缩效应对于永磁同步电机定子振动噪声的影响是真实存在的。
为了更加真实地反映定子的振动特性,对定子铁心进行谐响应分析。选择定子轭部一定点A,计算在电磁力单独作用时和考虑磁致伸缩效应时该点的振动速度,得出的谐响应分析结果如图7所示。
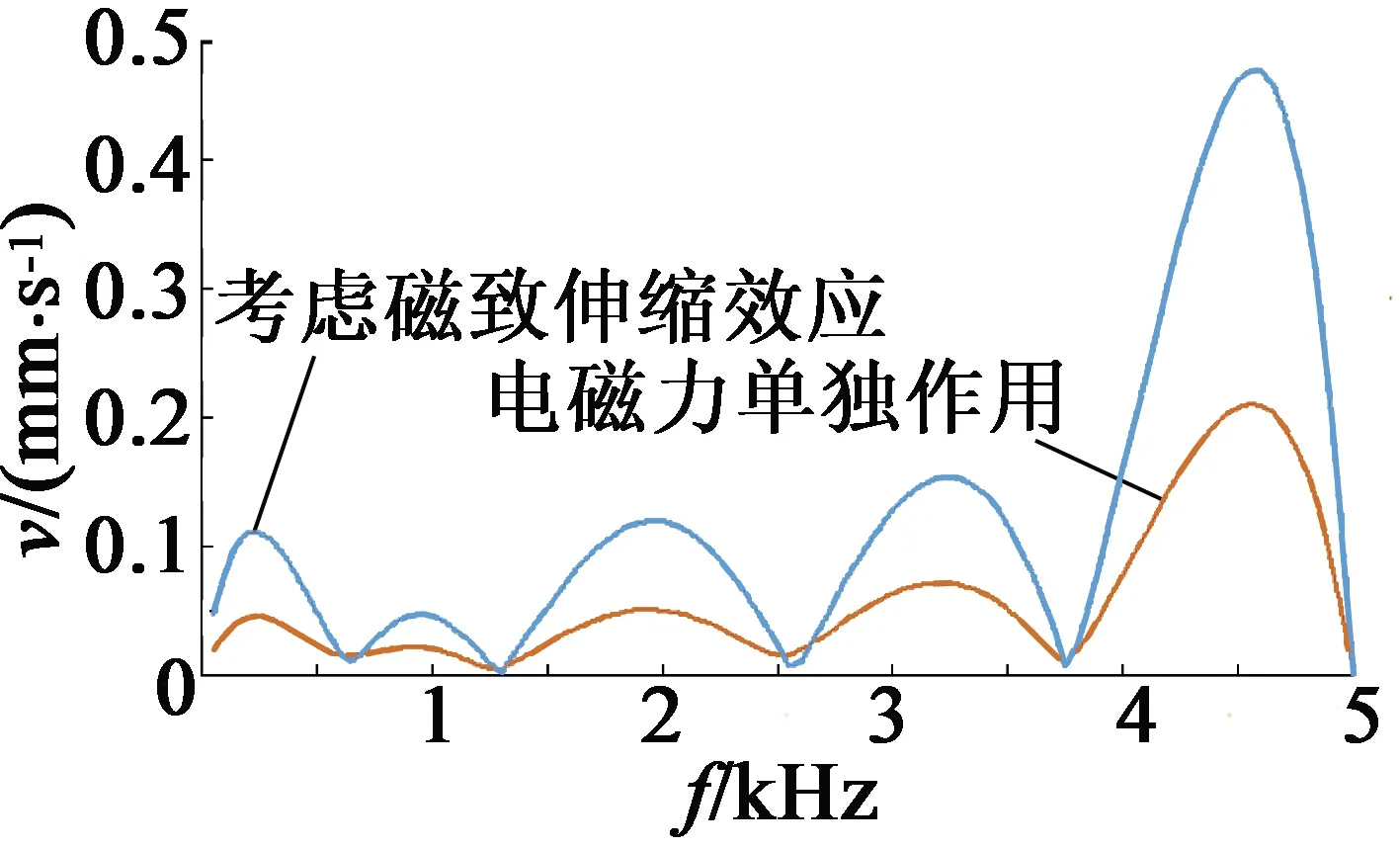
图7 A点振动速频谱图
由图7谐响应分析对比中可以看出,在考虑磁致伸缩效应时,A点的振动速度明显增加,振动速度最大值与电磁力单独作用时相比增加了1.23倍。
在谐响应分析的基础上,通过ANSYS Acoustic模块对电机定子铁心的噪声响应进行了分析与计算。首先在电机外建立一个半径1 m的空气包作为声场响应计算区域,得出电磁力单独作用、考虑磁致伸缩效应的声压级曲线,如图8所示。
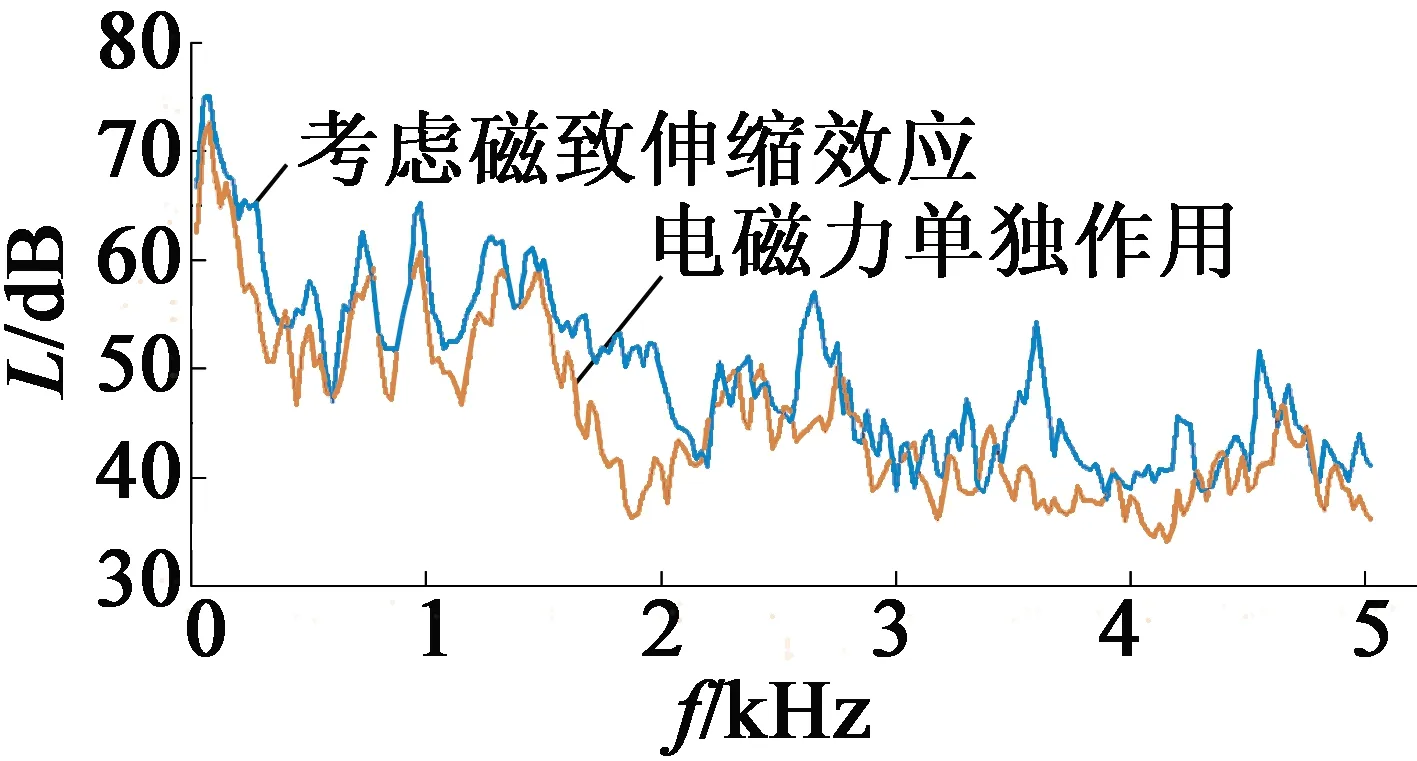
图8 考虑磁致伸缩效应和电磁力单独作用时声压级曲线
通过图8的噪声声压曲线可以看出,考虑磁致伸缩效应时,定子周围的噪声明显大于电磁力单独作用时的噪声。
3 结 语
本文建立了电磁-机械耦合数值模型,并在有限元软件中进行仿真,分别对永磁同步电机在电磁力单独作用时和考虑磁致伸缩效应下进行了振动仿真,并得出了以下结论:
在磁致伸缩效应的作用下,定子齿径向力密度幅值和最大齿部变形比电磁力单独作用时分别增加了13.1%和13.4%,且振动速度的最大值增加了1.23倍,声压级分布也明显增大。因此,磁致伸缩效应对于电机振动有重要贡献。为了在特殊场合满足永磁同步电机对振动噪声的要求,在电机设计计算阶段应考虑磁致伸缩效应。
