改进的干扰机集群任务分配算法*
2020-07-09董玉浩赵学军袁修久包壮壮李嘉林梁晓龙
董玉浩,赵学军,袁修久,包壮壮,李嘉林,梁晓龙
(空军工程大学研究生院, 西安 710051)
0 引言
在无人机集群执行突防任务时,敌方组网系统[1]能够精确、迅速地实现对突防编队的定位、追踪和打击,这使得集群突防面临巨大代价,而干扰机具有生产成本低、设备要求低、生存能力强等特点[2],能够在低空实现对组网雷达的干扰,达到掩护我方无人机的目的。
随着组网系统目标检测识别技术[3]和调度方法[4-6]的不断改进,传统的“一对一”干扰无法达到预期的效果,协同干扰的意义愈加凸显。在协同干扰任务中,干扰机集群面临两大问题:资源的优化分配[2,7-10]和虚假航迹的生成,前者的目的是实现干扰效率的最大化,后者旨在合理分配任务,完成协同干扰。针对任务分配,鲁晓倩,吴玉清,马来涛,赵辉[11-14]综合研究了协同干扰的原理和欺骗式干扰对无人机的要求,给出了干扰信号的功率计算方法,并基于几何原理给出了协同干扰的模型,整合出生成虚假航迹的各类任务分配算法,这些算法无法适用复杂的环境和机动条件,张翔等[15]改进了分配策略,但仍未提升算法的实用性。文中基于飞行动力学,构建单机搜索模型,结合航迹点分配和数量优化等手段改进了任务分配算法,通过仿真验证了其实用性和优化效果。
1 组网雷达的的协同干扰
1.1 “一对一”干扰模型
干扰机在截获雷达发射的侦察信号后,对该雷达采取噪声压制的手段[15],并使用特定的功率[14]延时发射干扰信号,考虑到无线电在空气介质中的传播速度极快,此时的干扰机与假目标、雷达必须在误差允许范围内共线。由于噪声压制,雷达只能接收到假目标信号,如此即完成了该时间点的干扰,如观测数据中出现与机动条件不符的点,则应进行异常值处理[16]。
1.2 数据融合与协同干扰
相位和幅度相同的组网为相干组网,否则为不相干组网,后者的雷达单站间存在机制差异,解决这种差异需要数据融合技术[14],其原理是:雷达侦获信息并传输到中央处理系统中,系统通过集中管理和数据分析,有依据地关联和融合,舍弃无效信息,并将处理后的信息发射回雷达。协同干扰是基于“一对一”干扰实现的,判断其实现的依据为是否通过“同源检测”[12],即在误差允许的范围内,不少于规定数量的雷达同时检测到目标航迹点在同一位置。
2 基于几何误差的任务分配算法
2.1 几何误差模型
干扰机集群能够随机生成虚假航迹[15],但由于机动性能限制和任务要求,假设干扰机均执行匀速直线运动,且需要生成既定的虚假航迹。
投影误差是常见的误差模型,其规则是:平面外一点可以被其在平面上的投影点代替,当且仅当它距平面小于给定误差,此类误差约稳定在2 m[17]。基于该模型,空间中无人机的匀速直线运动轨迹可作为平面上的匀速直线运动来讨论和求解。
2.2 基于几何误差的任务分配算法
假设组网中共有r部雷达,需要在n个虚假航迹点上实施干扰。基于几何误差判定模型的算法流程如图1。
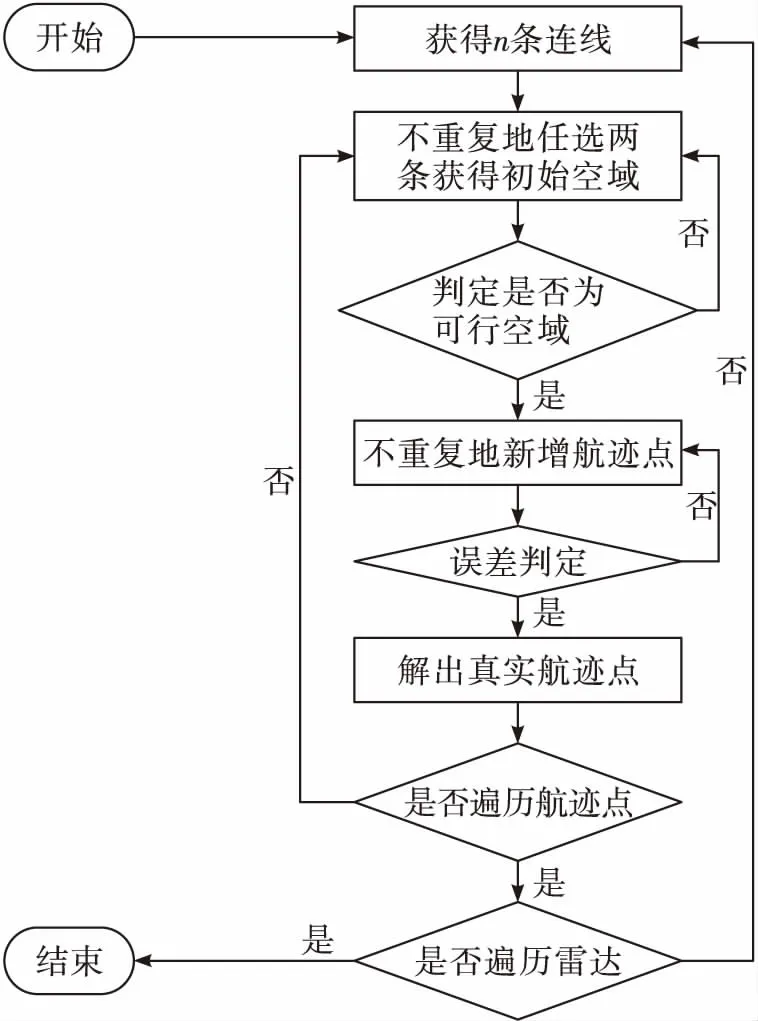
图1 基于几何误差模型的任务分配算法
3 算法改进
3.1 单机搜索模型
上述算法无法优化分配方案,且不适用于复杂机动的情况。文中根据雷达的误差产生原理[18]构建单机搜索模型,该模型的约束可简化为:若无人机的某段航迹始终在误差限内,那么这段航迹可以被认为是直线。
因此,在获取一条真实航迹时,可以由初始的真实航迹点Pi出发,以速度约束为条件,搜索下一个航迹点Pj,判定Pi与Pj之间是否满足飞行距离约束:
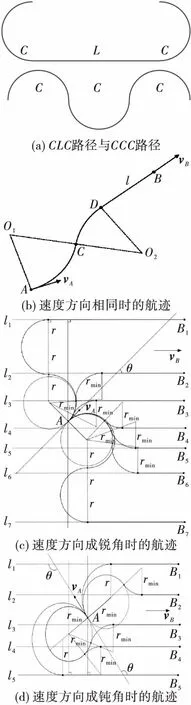
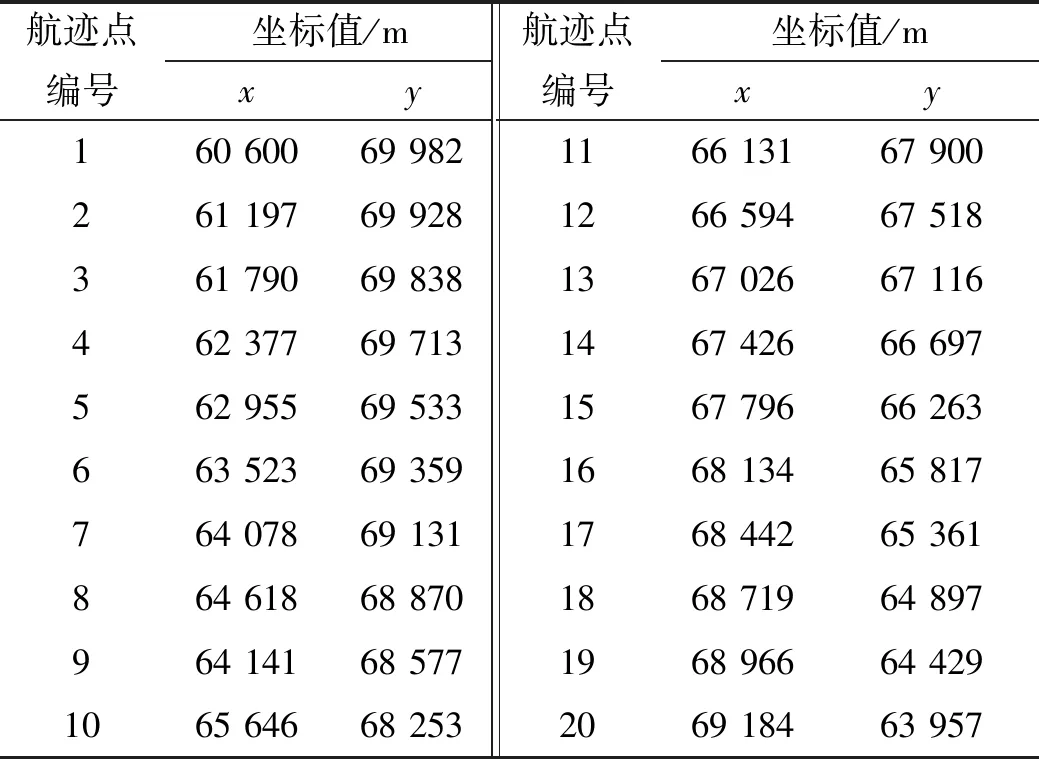
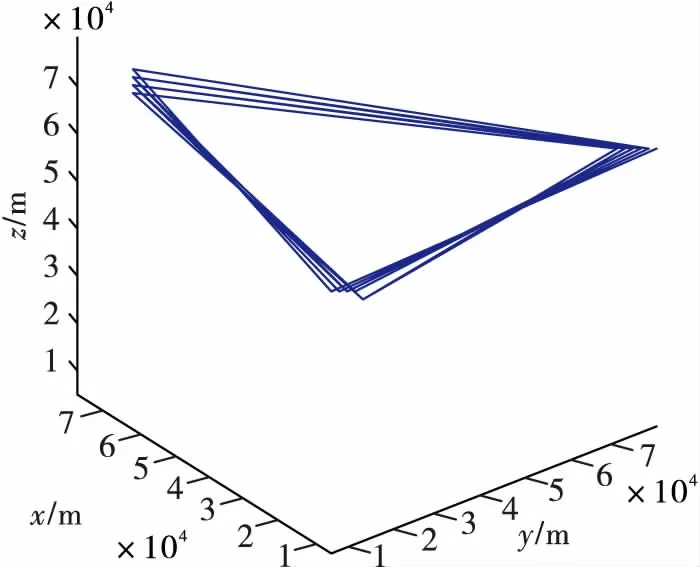
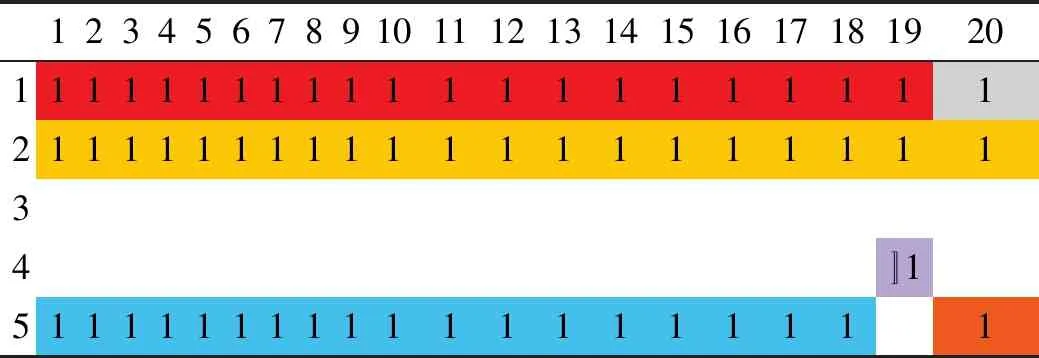
vmin(tj-ti)<|di,j| 式中:vmin是无人机的最小速度;vmax是无人机的最大速度;di,j是Pi到Pj的航线向量;ti是点i所在时刻;tj是点j所在时刻。 对于满足约束的点Pj,从该点向后搜索,接下来搜索到的每一点k都要进行距离约束判断和角度约束判断,且要保证误差限不变: 式中:dj,k是Pi到Pj的航线向量;tk是点k所在时刻;angle-errormax是角度误差限;velocity-errormax是速度误差限。 保留满足条件的航迹点,即获得一条真实航迹。 为了直观存储3.1中的搜索结果,建立状态矩阵G如表1,其r行对应r个雷达,n列对应n个待生成的虚假航迹点。 表1 虚假航迹点状态矩阵G 在分配真实航迹点之前,矩阵G=0。 Step1 在雷达i的第j个虚假航迹点上分配一架干扰机; Step2 从该点开始,使用单机航路生成算法生成一条航路Lj,在误差限内计算该航路覆盖的虚假航迹点数Np; Step3 在生成的历代航路中,最优航路为LB,虚假航迹点数的最大值可表示为Nmax;判定Np≥Nmax,是则Np=Nmax,LB=Lj,转Step4,否则直接转Step4; Step4 判定是否遍历所有从该点出发的航路,是则输出LB和Nmax,否则转Step2。 无人机数量优化算法(第二层优化)设计如下: Step1 在r部雷达上均增加一架无人机,分别用上述算法解出最优航路LBk及其对应的覆盖点数Nmax-k,其中1≤k≤r; Step2 删去Nmax-k最小的(r-s)条航路。 基于3.1~3.4的方法,可以设计改进后的算法流程如图6所示。 图2 双层优化算法 算法运行结束后得到的最终状态矩阵即为干扰机集群的任务分配方案。 在复杂机动条件下,干扰机的机动动作不仅限于匀速直线,但仍受到速度和转弯角(曲率)等的机动限制,结合3.1中的距离约束,引入Dubins路径来构造飞行动力学模型。根据文献[19]中的论述和证明,在有上述限制的路径规划中,两有向点之间的最短可行路径可能是图3(a)中CLC路径、CCC路径或这两种路径的子集(例如弧度不超过π的圆弧)。 图3(b)~图3(d)基于Dubins路径的原理,给出了两相邻虚假航迹点A和B之间的飞行航迹的3种情况。 图3 飞行路径与飞行航迹 这种条件下约束条件仅剩飞行距离约束,即: d(Pj,Pj+1)≤vmax(tj+1-tj) 组网中共5部雷达,“同源检测”的数量要求是3部,每部的最大作用距离均为150 km;无人机的飞行速度控制在120~180 km/h,飞行高度控制在2~2.5 km,最大加速度不超过10 m/s2;由于安全等因素的考虑,无人机间距需控制在100 m以上。雷达与虚假航迹点坐标见表2,误差限取为2 m,使用Matlab编程。 表2 虚假航迹点坐标值表 1)在干扰机只做匀速直线运动时,基于“同源检测”进行航路预规划,可知至多需要30架无人机完成协同干扰;改进前算法解出的干扰机集群航路见图4,任务分配见表3;改进后算法解出的干扰机集群航路见图5。 图4 改进前算法的航迹仿真结果 表3 改进前算法的任务分配 无人机号1234567891011121314到达时刻1611151817121716101418离开时刻510141720611162059131720干扰雷达11111222233333 图5 改进后算法所得航迹 2)取消匀速直线运动的限制,改进前算法无法求解,改进后算法解出状态矩阵如表4。 表4 复杂机动条件下解出的状态矩阵 分配优化共产生5架无人机,根据数量优化删去3号和4号,剩下3架分别为表中的红、橙、蓝,它们可以生成前18个虚假航迹点,现需要在点19新增1架、点20新增2架(灰、紫、褐),依据最大距离判定(该例中为500 m)与多无人机的运动控制原理[20],这3架只能单独完成干扰,因此该状态矩阵为复杂机动条件下的最终状态矩阵。 1)两种算法均适用于匀速直线运动的情况。此时算法一虽然得出了14架的结果,但其航迹仿真结果(图4)中出现了大量的不可实现点;改进后的算法解出27架干扰机,在可接受范围内,且所求航迹均可实现。 2)在复杂机动条件下,传统算法无法求解该算例,改进后算法仅用6架无人机即可完成协同干扰,实现了数量优化。 结论:改进后的误差模型符合雷达测量原理;改进后的单机搜索模型符合飞行动力学,解出的航迹能够实现,适用于多种机动条件,优化效果明显。3.2 数据存储的矩阵方法
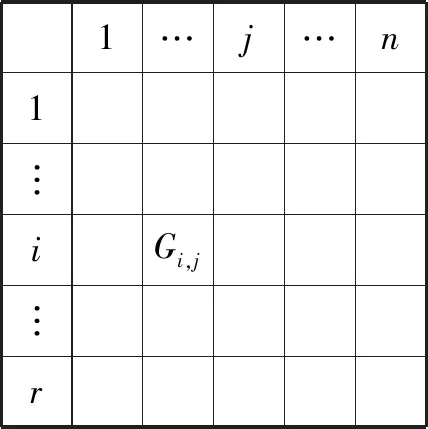
3.3 真实航迹点分配
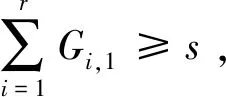
3.4 无人机数量优化
3.5 双层优化算法流程

3.6 复杂条件下的飞行动力学模型
4 仿真与实现
4.1 算例说明
4.2 两种算法的仿真结果对比
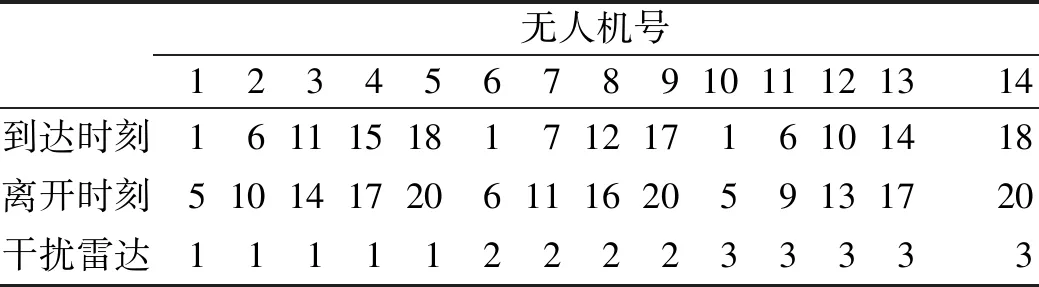
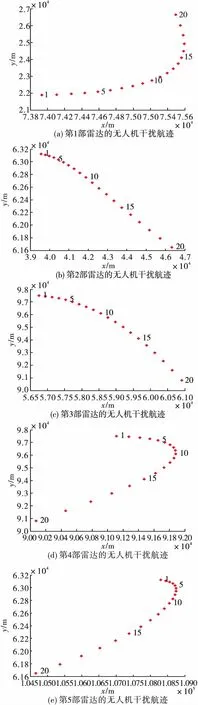
4.3 结果分析与结论
