基于神经网络补偿动态逆误差的导弹控制器设计*

常怡鹏，王小平，林秦颖，王晓光，董昕瑜

(空军工程大学航空工程学院，西安 710038)

0 引言

导弹作为一个复杂的非线性被控对象，常用的控制方法是先对导弹的数学模型进行小扰动线性化，再用常规的线性化控制方法对线性化的状态方程进行控制[1]。但是随着导弹的超机动以及非常规机动性能的提高，这种方法已经不能满足需要。近年来，各种非线性控制方法成为研究的热点，如鲁棒控制[2],滑模自适应控制[3]等。这些非线性动态逆控制方法由于具有良好的控制性能已经广泛的被导弹的姿态控制系统所应用[4-6]。基于非线性动态逆控制的设计方法，运动过程中所有的非线性信息[7]以及导弹运动状态之间的耦合信息全都包含其中。既解决了回路之间的解耦，还解决了非线性系统的控制问题，使得导弹控制系统从传统的三通道设计转变成整体的设计。但是这种方法过度依赖被控对象的精确模型，而控制系统由于非线性、外在干扰以及未建模动态特性，无法获得精确的模型[8-10]。从而导致控制器具有较差的鲁棒性。近年来的研究表明，多层感知器神经网络自适应参数是非线性的，并且具有以理想精度逼近平滑非线性函数的能力[11]，所以可以用于补偿动态逆误差。

为了有效的降低控制系统的跟踪误差，提高系统的鲁棒性，文中在考虑模型不确定性的基础上采用神经网络对逆模型误差进行动态在线补偿。

1 导弹数学模型的建立

导弹在飞行过程中受到气动力、主推力以及重力作用[12]：

(1)

式中：Xa、Ya、Za为气动力在弹体坐标系下的分量；Px、Py、Pz为主推力在弹体坐标系下的分量；Gx、Gy、Gz为重力在弹体坐标系下的分量。

由于重力在Oy垂直方向上的分量为零，因此Py=Pz=0。在弹体坐标系下，将重力矢量进行投影，可以得到：

(2)

最终合外力的表达式为：

(3)

由于导弹的飞行高度、速度、角速率以及姿态角均能够影响导弹的气动力和气动力矩[13]，所以导弹的气动力和气动力矩由导弹的气动外形和运动状态所决定，表达式近似如下：

(4)

(5)

由导弹绕质心转动的动力学和运动学方程可得：

(6)

(7)

2 动态逆控制器的设计

状态变量在动态响应过程中具有时间尺度差异的特点，文中采用层叠结构控制的思想来选取两组变量[14-15]，一组慢变量：俯仰角ϑ、偏航角ψ、滚转角γ；一组快变量：ωx,ωy,ωz3个角速度。在求解快变量子系统时，可以认为俯仰角ϑ、偏航角ψ、滚转角γ是常量。通过上述分析，将系统分为慢回路和快回路并设计相应的姿态控制器。

为了使得快回路能够快速精准的跟踪慢回路[16]，设计快回路的带宽是慢回路带宽的3～5倍。系统控制器设计的框图如图1所示。

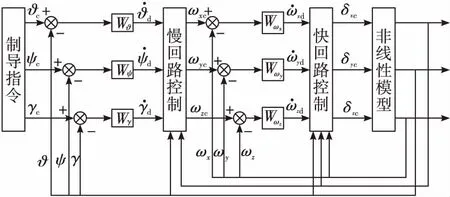
图1 导弹控制系统结构示意图

基于上述导弹动力学和运动学模型，分别得到控制器的慢回路运动方程以及快回路运动方程：

(8)

(9)

2.1 慢回路姿态控制器的设计

根据慢回路运动方程设计慢回路的动态逆控制器的控制律。

由式(7)可以得到导弹的慢回路运动模型：

(10)

式中：xf=(ωx,ωy,ωz)T,xs=(ϑ,ψ,γ)T

(11)

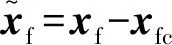
(12)

当t→，上式变为:

(13)

由于可逆，则令xsc=(ϑc,ψc,γc)T, 定义跟踪误差为:

(14)

取慢回路输出为(ϑ,ψ,γ)，由于gs(xs)可逆，对式(9)进行反馈线性化，可得控制律如下：

(15)

式中：Ws=diag(Wϑ,Wψ,Wγ)，Wϑ、Wψ、Wγ均大于零。

将上式代入式(12)中可得到慢回路的闭环特征方程：

(16)

下面进行控制器稳定性的证明：

(17)

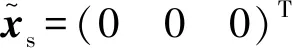
(18)

则有：

(19)

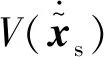
2.2 快回路姿态控制器的设计

根据快回路运动方程设计快回路的动态逆控制器的控制律。

由方程(8)可得到导弹快回路的动力学模型：

(20)

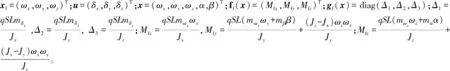
当Δ1Δ2Δ3≠0时，gf(x)矩阵可逆，则令xfc=(ωxc,ωyc,ωzc)T,定义跟踪误差：

(21)

快回路的输出为ωx、ωy、ωz,又因为gf(x)矩阵可逆，对式(19)进行反馈线性化，可以得到控制律如下：

(22)

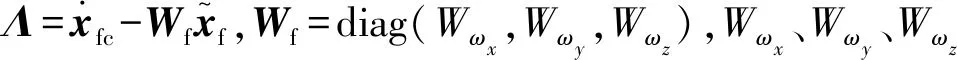
将上式代入式(19)中可以得到快回路的闭环特征方程：

(23)

快回路稳定性证明在此不再赘述。

3 神经网络补偿逆误差

3.1 逆误差的产生以及跟踪动态特性

根据上述非线性动态逆方法，设计的控制量为：

(24)

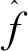
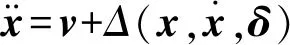
(25)

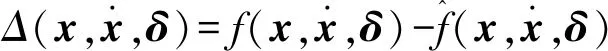
文中神经网络系统结构是基于神经网络模型参考自适应控制[17]，结构图如图2所示。

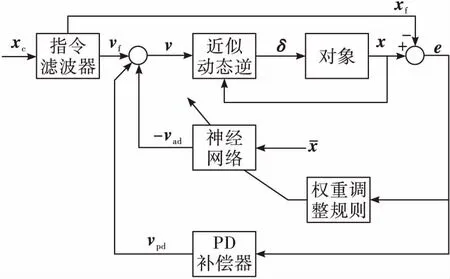
图2 基于神经网络的自适应控制结构

指令滤波器作用是对指令信号进行滤波以得到理想的指令响应。设伪控制信号为：

ν=νpd+νf-νad

(26)

式中：νf为指令滤波器输出的伪控制信号；νad为自适应神经网络的输出；νpd为PD补偿器的输出。

PD补偿器的设计采用线性控制理论，输出的伪控制量为：

νpd=[KdKP]e

将式(26)代入式(25)中可以得到舵偏指令的跟踪误差的动态特性：

(27)

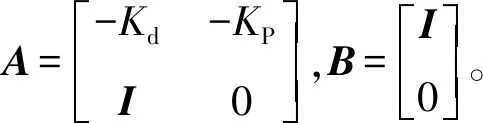
由式(26)可知用自适应神经网络的输出项νad能够重构动态逆误差的话，系统的指令跟踪误差将渐进趋向零。

3.2 神经网络结构

文中重构动态逆误差[18]采用单隐层神经网络结构，如图3所示，输入输出关系式为：

式中:σ(·)为激励函数;N1、N2、N3代表神经元的个数，它们分别属于神经网络输入层、中间隐含层和输出层;vjk、wij代表层与层之间的权值，分别属于输入层到隐含层，隐含层到输出层。

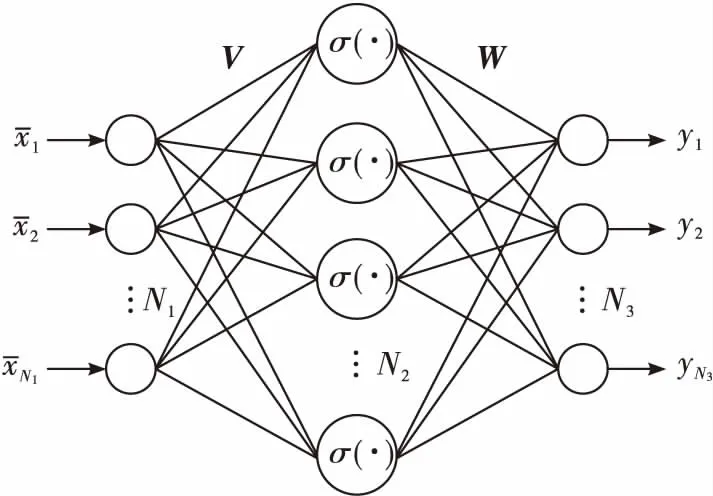
图3 单隐层神经网络结构

由单隐层神经网络全局近似定理,存在有限个神经元数N2以及重构逆误差的理想权重矩阵W′和V′使得：

(28)

式中：Δ代表的是非线性动态逆误差函数，εN满足εN>0，是任意给定的逆重构误差。

式(26)中的自适应项为：

(29)

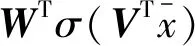
(30)

网络的逼近性能通过在线实时更新神经网络各层之间权值以及各神经元阈值来保证，从而体现出在线补偿的特性。

4 仿真结果分析

4.1 无补偿逆误差的情况

用Matlab/Simulink搭建导弹的动力学、运动学模型以及导弹的控制模型，在这里Wωx=Wωy=Wωz=50 s-1，Wϑ=Wψ=Wγ=10 s-1，在验证设计的控制器时，需要考虑到舵机的实际转角限制，初始条件如下：V=500 m/s，导弹质量M=1 840 kg，指令姿态角γc=0°，实际舵机转角限制为±15°。

为了验证控制器的稳定性和控制的精准性，现在将指令信号设为正弦信号γc=0°，ϑc=ψc=sin(0.2π·t)/57.3，仿真结果如图4～图6所示。

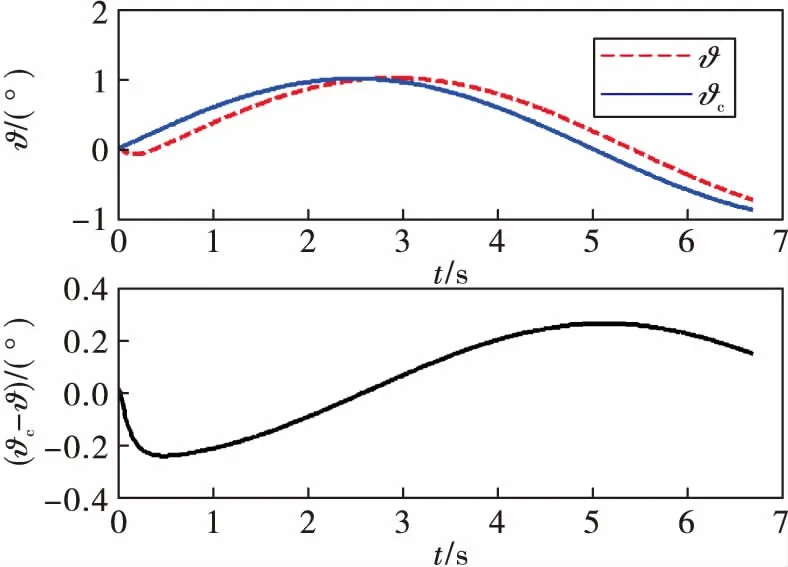
图4 俯仰角跟踪曲线

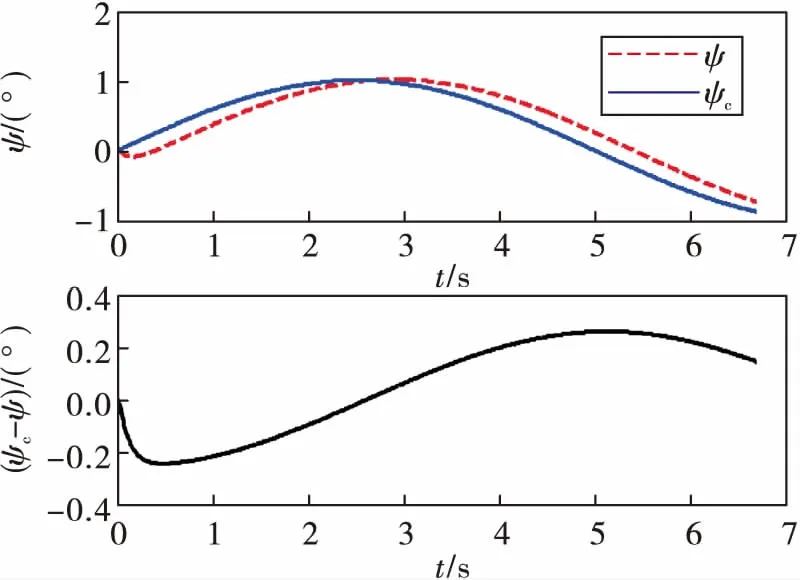
图5 偏航角跟踪曲线

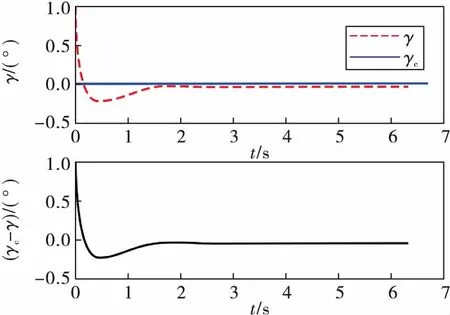
图6 滚转角跟踪曲线

由图4、图5可知，控制器在跟踪俯仰角和偏航角指令信号有较大的跟踪误差，在第5 s时的跟踪误差最大分别达到了0.25°和0.27°，跟踪精度不理想。由图6可知，在跟踪滚转指令信号时，超调量较大。

4.2 神经网络补偿逆误差的情况

对导弹飞行期间的主要控制量即3个姿态角分别设计神经网络控制器从而改善系统的性能。为了使权重矩阵包括隐含层和输出层神经元的阈值，在输入层和隐含层之间增加一个神经元，该神经元输出为常数并且与下一层神经元之间的阈值实时调整，设置神经网络需要调整的连接权重数量为68个，神经网络的输入层、隐含层和输出层神经元数目分别为5、10和1。同样将指令信号设为正弦信号γc=0°，ϑc=ψc=sin(0.2π×t)/57.3。并且将气动参数摄动20%，仿真结果如图7～图9所示。

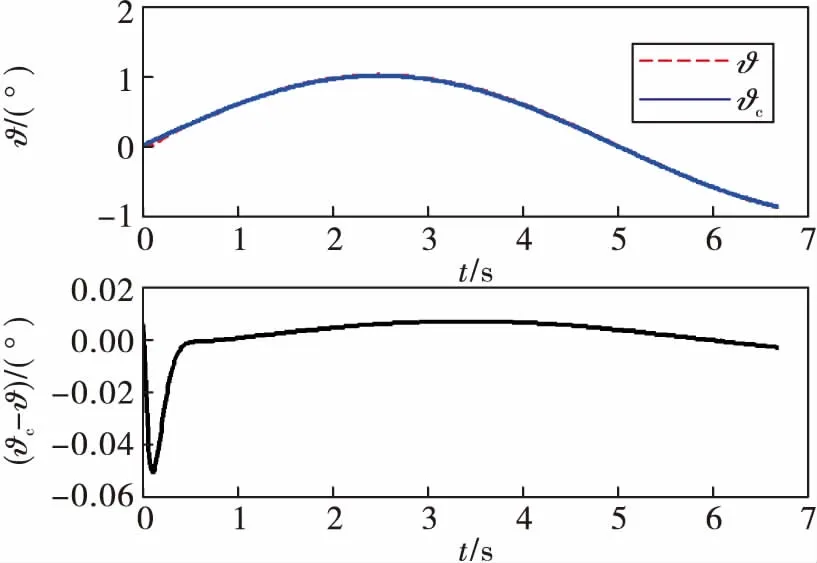
图7 俯仰角跟踪曲线

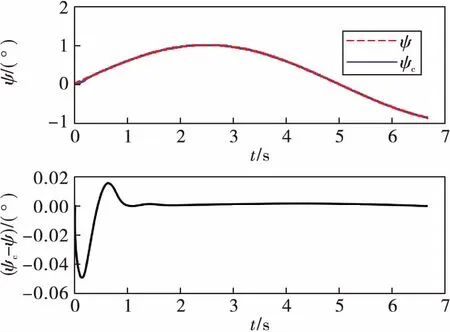
图8 偏航角跟踪曲线

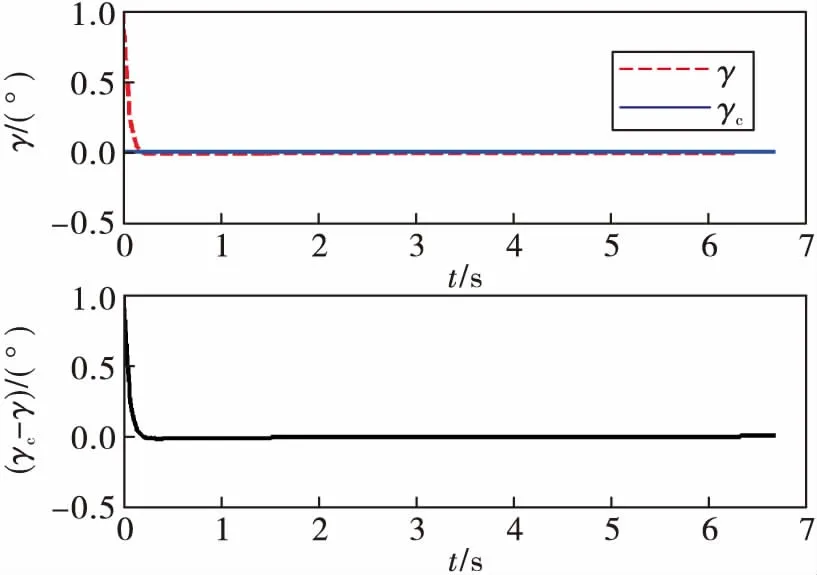
图9 滚转角跟踪曲线

从图7到图9可以看出，在加入神经网络补偿系统逆误差之后，俯仰角和偏航角的跟踪误差明显降低，最大误差为0.05°，并逐渐趋向于0。对于滚转角的跟踪，超调量相比于误差补偿前也有明显的减小。同时，系统在气动参数摄动20%后，仍具有良好的性能，满足工程实际需求。

5 结语

文中基于神经网络全局近似的思想，重构非线性动态逆控制器的逆误差，设计了一种具有动态逆误差补偿的控制器。与单一非线性动态逆控制器相比，该方案充分利用动态逆控制中的设计信息，实现了逆误差的补偿。使得非线性动态逆控制方法能够满足工程的实际需求。从仿真结果可以看出，用神经网络对逆误差进行补偿后，控制系统具有良好的稳态性能和较强的鲁棒性。