弹丸不同结构参数对弹丸挤进的影响分析*

蔡翘楚，杨 臻，蓝维彬

(中北大学机电工程学院， 太原 030051)

0 引言

弹丸的挤进是枪械发射的重要过程，它直接决定了整个内弹道过程。弹丸挤进过程的实质是弹丸在受到高温高压火药燃气的作用下与弹壳发生脱离进而嵌入膛线[1]。弹丸各部分的参数变化对弹丸的挤进影响程度不同，对枪械射击影响较大。

弹丸挤进过程是枪/弹匹配设计方面的重要研究内容，国外在该领域有较深入的研究，并已形成较详细的规范。在枪管内膛方面，美国雷明顿公司将枪管膛线形状采用多弧形或多边弧形以保证枪管寿命和射击精度；在弹药方面，为了降低枪管内膛磨损，国外枪弹弹丸被甲材料基本采用铜合金，而近些年又在枪弹表面涂层有了较大的进展；在内弹道、枪/弹匹配方面，美国陆军研究与发展司令部，以Ml6Al、M4、M134为研究对象，研究了热耦合下的弹丸膛内运动状态。

我国自动武器的口径系列基本沿用了前苏联的标准，并且多年来一直没有进行过系统、深入的研究和改进优化；而在新口径如5.8 mm、8.6 mm等枪械的研究过程中可借鉴、移植的技术储备较少, 现有的理论分析往往是不完善、不系统的，因此针对某型小口径步枪建立了弹丸挤进仿真分析模型，考虑挤进过程中多种初始条件，从内膛与弹药结构参数两方面分析不同参数对弹丸挤进的影响。

1 挤进数学模型建立

本节通过建立弹丸圆柱部挤进数学模型，以数值分析的方法计算弹丸挤进力，并找到挤进力的变化规律。

1.1 基本假设

弹丸挤进过程从弹丸前端面与坡膛刚好接触开始。由于弹丸圆柱部直径大于枪管内径，当弹丸向前运动时，随着挤进过程的加剧，枪管材料处于屈服或流动状态，被逐渐推到后方，接触面积将逐渐增大，阳线会在弹体表面留下刻痕[2]。在计算弹丸挤进过程中，作以下假设：

1)弹丸与坡膛之间应力保持不变，在挤进条件下，刻槽与变形的应力为材料在准静态实验下的屈服极限值σf。

2)挤进力的变化是由接触面引起的，有：F=σf·S，S为接触面积。

3)文中研究的弹丸体最大直径超过阴线直径，认为接触发生在阴线与阳线的圆周线上及其导转侧表面。随后，由于阳线推挤下来的材料填入阴线，接触也会在阴线上出现。这种情况下，挤进力-行程曲线上升斜率开始很低而后来会突然间断式上升。

4)将弹丸头部与坡膛接触点和弹丸圆柱部前端简化为斜坡面，对弹丸尾端不作处理。

根据以上假定，可确定挤进力-位移曲线，弹头弧形部前倾角α和坡膛锥角φ的关系，分为α>φ和α<φ两种情况考虑。

1.2 挤进力公式推导

参考文献[3]与文献[4]中对5.8 mm狙击步枪弹和火炮弹带挤进力的计算方法，考虑该步枪弹的结构，推导挤进力计算公式。其中d0为阳线直径，d1为阴线直径，dp为弹头最大外圆直径，φ为坡膛锥角，θ膛线缠角，α为弹头弧形部前倾角，μn为静摩擦系数，a为阳线宽度，b阴线宽度，σf为材料在准静态实验下的屈服强度。

图1 挤进结构示意图

根据该条件下结构特点，将挤进过程分为以下4个阶段：

第一阶段：A点到A′点，位移l1=s=s2-s1。

第二阶段：A点到O点，位移l2=s2。

第三阶段：B点到O点，弹丸连同延伸部分全部挤进身管，即位移l3=s2+△s。

第四阶段：弹丸完全挤进膛线，位移l4>s2+△s。

每一阶段对应的挤进阻力Fx表达式分别为：

(1)

Fx2=σf·π(μncosφ+sinφ)·(d0+s1tanφ)·

(2)

(3)

(4)

(5)

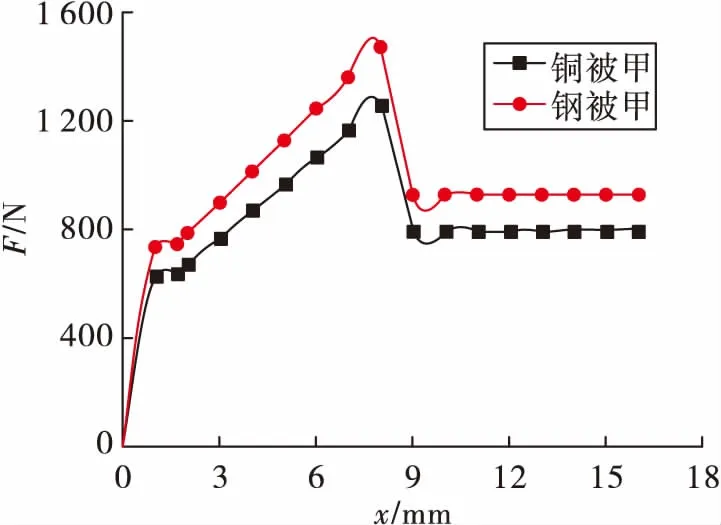
图2 计算曲线

图2为不同被甲材料弹丸挤进时轴向挤进阻力的计算曲线。由图2可知，随着弹丸行程的增加，挤进阻力先呈上升趋势，在达到峰值后下降，最后趋于平稳。由于钢被甲材料的屈服强度更高，使其产生塑性变形所需要的力更大[5]。因此，钢被甲弹较铜被甲弹挤进阻力更大[6]。弹丸及枪管各部分材料的力学性能如表1所示。

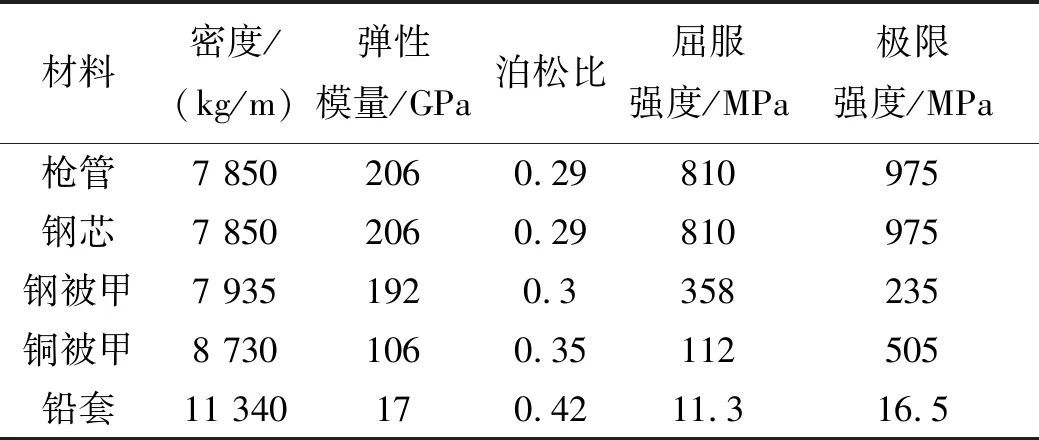
表1 材料机械性能参数

2 弹药结构差异对挤进的影响分析

2.1 分析模型建立

2.1.1 网格划分

对计算模型进行网格划分，网格类型以六面体缩减积分实体单元为主，其中枪管共划分168 530个网格，弹丸被甲共划分50 140个网格，铅套共划分12 576个网格，钢芯共划分5 048个网格，弹壳共划分14 687个网格，计算模型如图3所示。

图3 枪管膛线及弹丸被甲网格划分

2.1.2 施加载荷

载荷施加过程中由于枪管只取了一小段结构，因此只考虑弹丸的重力作用，对枪管尾部圆柱约束了全部自由度；同时对弹丸的载荷施加根据火药燃气在膛内的压力曲线添加载荷，并对各部件之间施加摩擦接触。

挤进中身管作为弹丸挤进的外部约束，而身管在火药燃气热冲击作用下，材料机械性能发生变化；同样，弹底在受到热冲击时温度的变化而导致材料性能的变化。因此，不同的温度下挤进也不同，仿真分析时，需要建立多个温度状态下的挤进模型。而计算时枪管只取了一部分，为了使弹丸完全挤进枪管，而且不影响最后求出的挤进压力，故对弹丸施加位移载荷，位移-时间关系如图4所示。

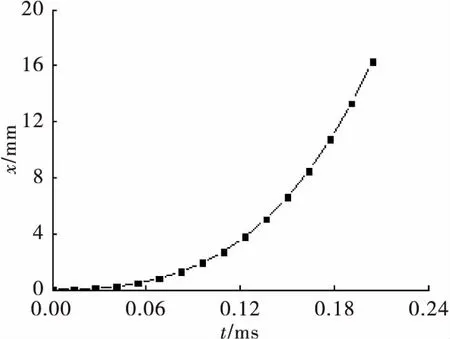
图4 位移-时间曲线

2.2 结果分析

2.2.1 不同弹丸结构差异分析

本节主要考虑弹丸圆柱部结构参数对挤进过程的影响。弹丸圆柱部尺寸根据枪弹弹头工艺图，将计算模型分为3个不同尺寸进行仿真分析，即小尺寸(弹丸圆柱部前端Φ5.92 mm，后端Φ5.98 mm)、中尺寸(弹丸圆柱部前端Φ5.96 mm，后端Φ6 mm)和大尺寸(弹丸圆柱部前端Φ5.98 mm，后端Φ6.01 mm)。

由于弹丸的圆柱部是直接与内膛膛线发生作用，因此从图5可以看出，挤进过程中弹丸圆柱部尺寸越小，弹丸被甲表面所受应力越小，枪管内膛对弹丸的作用越不明显。

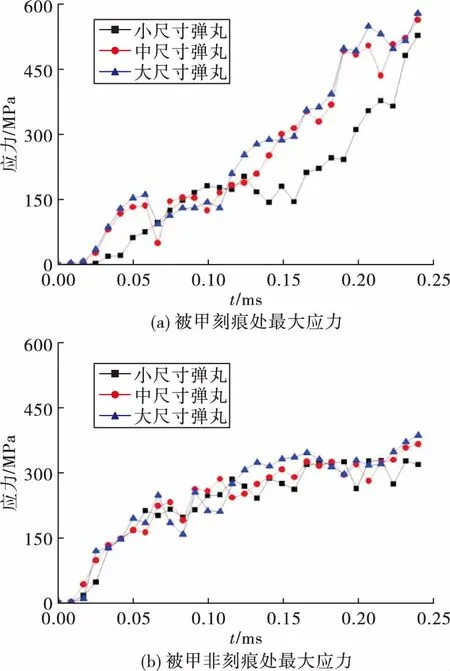
图5 不同尺寸弹丸挤进时表面应力

图6为弹丸挤进过程中弹丸绕质心的摆动情况。由图可知，弹丸圆柱部尺寸的大小对挤进时弹丸的运动状态有较大的影响。从挤进过程中弹丸的横向与纵向摆动幅度可以看出，圆柱部尺寸较小的弹丸在挤进时有较大的波动，而圆柱部尺寸较大的弹丸则相对平稳挤进。

弹丸圆柱部尺寸不同，使得弹丸在挤进过程中受力有一定的差异，如图7所示，不同尺寸弹丸挤进时所受轴向阻力变化情况。由图可知，弹丸圆柱部尺寸越大，所受的挤进阻力越大，挤进膛线的过程越困难。

2.2.2 弹药装配差异分析

本节主要考虑弹丸与弹壳的装配差异对挤进过程的影响，即弹丸与弹壳完全相同，全弹长变化。枪弹装配尺寸根据枪弹总装配图，将计算模型分为3个不同尺寸进行仿真分析，即上偏差尺寸(全弹长58 mm)、中间尺寸(全弹长57.5 mm)和下偏差尺寸(全弹长57 mm)。

由于在弹丸挤进膛线之前会发生弹丸与弹壳脱离过程，取弹丸被甲表面靠近样条曲线某处来研究应力变化情况。从图9中可以看出，在拔弹的过程中，该处由于没有和膛线接触，因此无较大应力变化。

因为枪弹的装配误差使得弹丸从拔弹过程到挤进膛线之间的距离有一定差异，导致在挤进前弹丸就发生摆动，且摆动幅度不同，对接下来的挤进过程有一定的影响。由图9可知，下偏差尺寸，即弹丸离膛线距离最大，在从拔弹到挤进整个过程中的波动要略大于中间尺寸和上偏差尺寸的枪弹。

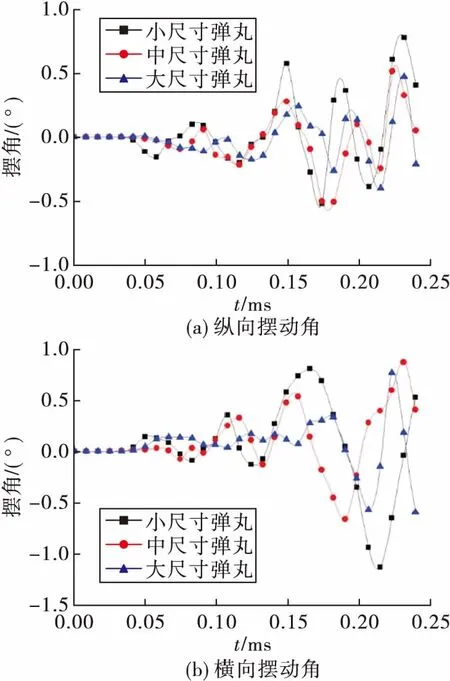
图6 不同尺寸弹丸挤进时绕质心摆动角

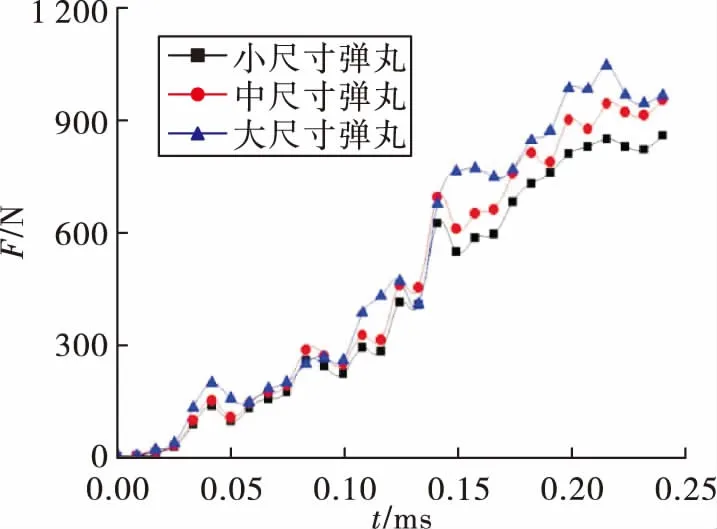
图7 不同尺寸弹丸挤进时的轴向阻力

图10为不同装配尺寸的枪弹所受到的轴向阻力，从图中可以看出，从拔弹到挤进膛线的过程中下偏差尺寸的枪弹所受的轴向阻力略高。这是因为弹丸离膛线较远，火药燃气对弹丸的作用时间较长，当弹丸到达膛线时弹底压力较大，弹丸轴向受力较大。

2.2.3 弹丸被甲材料差异分析

本节主要考虑弹丸被甲材料差异对挤进过程的影响。即弹丸与弹壳尺寸完全相同，被甲材料变化。采用5.8 mm制式铜被甲弹和钢被甲弹进行仿真分析。

由于材料的屈服极限不同，由图11可知，铜被甲刻痕效果较钢被甲明显，而钢被甲弹表面应力较铜被甲弹大。

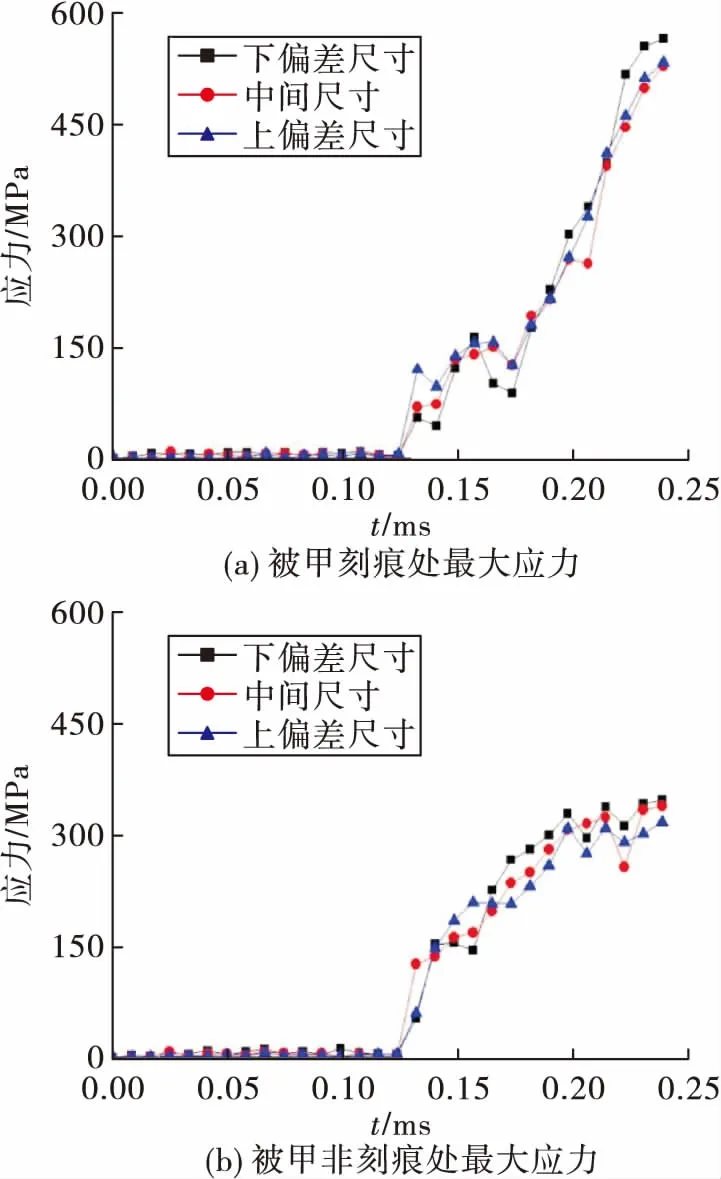
图8 不同装配尺寸挤进时表面应力

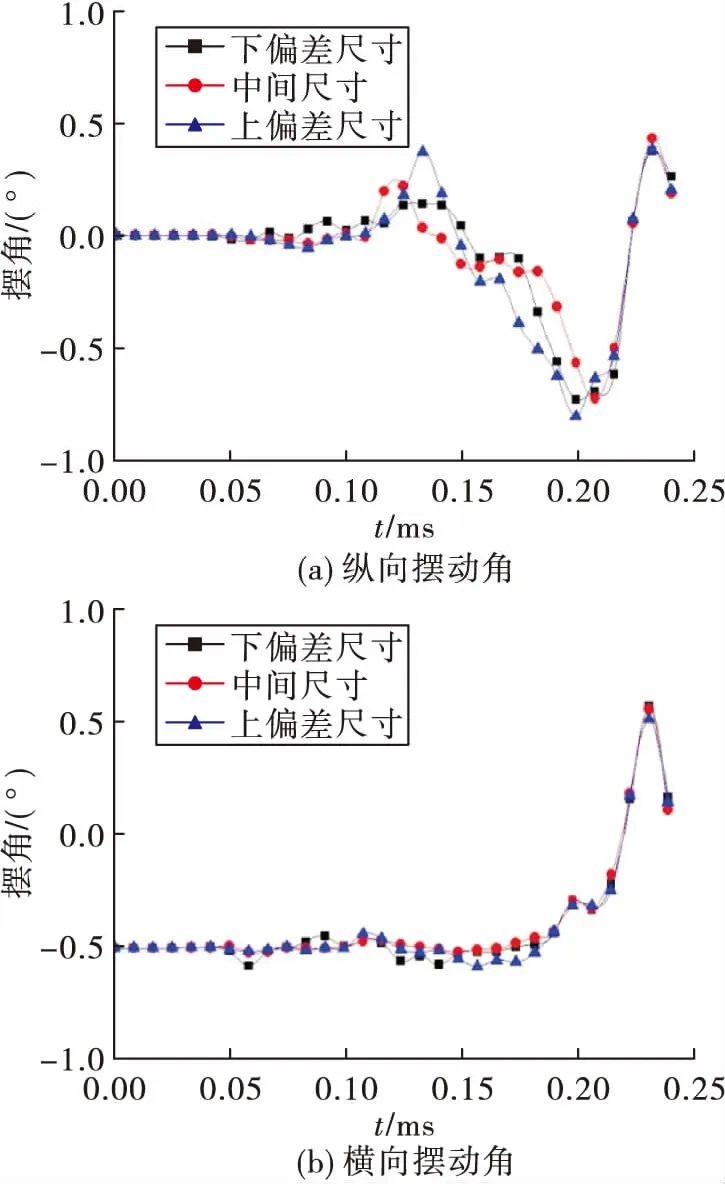
图9 不同装配尺寸挤进时摆动角

如图12所示为不同被甲材料挤进过程中弹丸绕质心摆动的情况。由于不同材料的刚度不同，弹丸被甲材料对挤进时弹丸的运动状态有较大的影响。铜被甲弹丸在挤进时有较大的波动，而钢被甲弹丸则能相对平稳的挤进。

图10 不同装配尺寸挤进时的轴向阻力

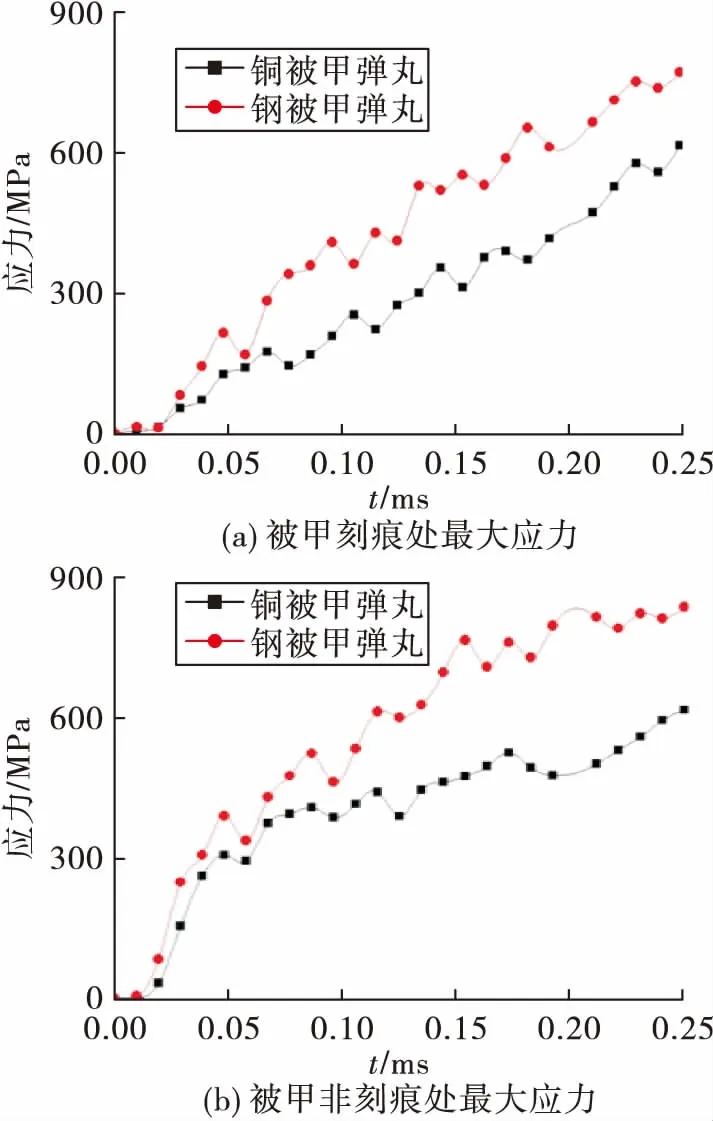
图11 不同被甲材料弹丸挤进时的应力

图13为不同被甲材料挤进过程中所受的轴向阻力，由于不同材料的屈服强度不同。由图可知在挤进膛线过程中铜被甲弹丸所受的轴向阻力较钢被甲弹丸所受的轴向阻力略小。

3 结论

文中以不同结构尺寸及不同被甲材料的枪弹为研究对象，建立挤进数学模型并进行有限元仿真分析，通过公式推导和仿真计算得出：枪弹的结构参数及材料均对弹丸所受的应力和轴向阻力等产生影响。

1)由于弹丸结构尺寸的不同，弹丸在挤进过程中所受的挤进阻力也有所不同。弹丸的全弹长越长，挤进过程越平稳。弹丸的圆柱部尺寸越大，弹丸挤进过程的波动越小。

图12 不同被甲材料弹丸挤进时摆动角

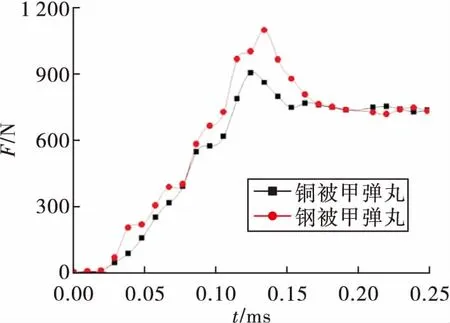
图13 不同被甲材料弹丸挤进时的轴向阻力

2)由于弹丸被甲材料的不同，两种弹丸与枪管内壁之间的摩擦系数也不同，导致铜被甲弹丸在挤进过程中所受的挤进阻力和应力较大，而钢被甲弹丸更能平稳的挤进。

该研究可为优化枪管和弹丸结构，选择弹丸被甲材料，进而为提高射击精度提供理论参考依据。