齿面磨损数值仿真方法综述
2020-07-08吴淼杰韩旭陶友瑞
吴淼杰 韩旭 陶友瑞


摘要 齿轮是机械传动中的重要基础元件,在航空航天、轨道交通、工程机械与精密仪器等领域有广泛应用,齿面磨损是齿轮的主要失效形式。首先,按照不同的磨损机理,分别综述了齿面黏着磨损和齿面疲劳磨损的数值建模研究,总结了磨损模型的4个发展阶段。其次,阐述了考虑系统动态响应、多种润滑状态及微观形貌演变的齿面磨损仿真研究,简述了国内外学者在该领域中的研究成果与存在的问题。最后,总结了齿面磨损数值仿真领域值得深入探索的问题,并对该领域的发展方向进行了展望。
关 键 词 齿轮传动;磨损预测;数值仿真;磨损模型;齿面磨损
中图分类号 TH132.4 文献标志码 A
An overview of numerical simulation methods for tooth wear
WU Miaojie1, HAN Xu1,2, TAO Yourui2
(1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha, Hunan 410082, China; 2. State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300130, China)
Abstract Gear is an important component in mechanical transmission, which is widely used in aerospace, rail transit, engineering machinery and precision instruments, etc.. The main failure form of gear is tooth surface wear. First of all, according to different wear mechanisms, the numerical modeling research of adhesive wear and fatigue wear of tooth surface is summarized, and the four development stages of wear model are also summarized. Secondly, the simulation research of tooth surface wear considering the dynamic response of the system, various lubrication states and micro morphology evolution is discussed, and the research results and existing problems of domestic and foreign scholars are described. Finally, the problems that are worthy of further exploration of numerical simulation of tooth wear are summarized, and its development direction is presented.
Key words gear transmission; wear prediction; numerical simulation; wear model; tooth surface wear
0 引言
齒轮具有传动精确、效率高、结构紧凑等特点,被广泛用于航空航天[1]、轨道交通[2]、工程机械[3]、精密仪器[4]等诸多领域,是传统机械中的重要基础元件。据统计,传动机械中约80%的故障是由齿轮失效引起的,约1/3~1/2的工业能源损耗是由摩擦磨损造成的,随着我国齿轮行业生产规模的不断扩大,由齿轮磨损造成的经济损失问题也愈发凸显,对齿面磨损问题开展研究具有重大的社会效益和经济效益。齿面磨损是一个齿面材料不断损失的连续过程,贯穿齿轮的整个服役周期,大致分为磨合阶段、稳定磨损阶段和剧烈磨损阶段。虽然齿轮的磨合过程能提高传动性能,但过度的齿面磨损会增大传递误差使传动精度降低,直接影响机械系统的服役寿命和工作可靠性[5]。齿面磨损会改变齿面载荷分布,影响齿轮系统的动态特性,产生严重的振动与噪声[6],恶化齿轮服役条件,缩短齿轮的工作寿命[7]。现代机械设备向高端化与精密化发展,对齿轮提出高速重载、精密低噪、长服役周期等要求,齿轮的磨损性能是齿轮能否长期稳定运行的关键,研究复杂齿面的磨损进程,揭示其磨损机理对于提高齿轮传动性能具有重要意义。
齿面磨损数值仿真研究包括磨损模型的建立和数值仿真2部分,磨损模型能够在一定程度上揭示齿面磨损机理,为数值仿真提供理论指导和工作基础;数值仿真是理论模型的实际应用,能够模拟齿面磨损进程,揭示各影响因素对齿面磨损的作用机制,二者缺一不可。本文首先分析了齿面磨损数值模型的发展阶段,然后,阐述了与齿面磨损数值建模相关的代表性研究,按磨损类型分别从齿面黏着磨损和齿面疲劳磨损两方面对建模研究进行综述,其次,讨论了齿面磨损与系统动态响应、润滑状态、表面形貌的耦合作用的研究现状及关键问题,系统地评述了现有的齿轮齿面磨损数值仿真研究方法,最后,对齿轮齿面磨损的数值仿真研究进行总结与展望。
1 齿面磨损数值建模研究
齿轮传动是基于齿面啮合的连续相互作用来传递动力的,在其服役周期内,齿面间的力学作用或化学作用会不可避免地引起磨损。按磨损机理,可将磨损分为四大基本类型:黏着磨损、磨粒磨损、腐蚀磨损和疲劳磨损。齿面磨损的影响因素较多,通常是多种磨损机理的复合作用,建立完全符合实际的齿面磨损模型有很大难度,目前,齿面磨损数值模型大多基于单一的磨损机理建立。多年来,学者们在齿面磨损方面进行了大量工作[8-12],建立了多种齿面磨损数值模型。
对现有文献归纳总结可知,磨损数值模型的发展大致可以分成4个阶段:第1个阶段的磨损模型为经验公式[13],只能够较为准确地预测特定试验工况和一定数据范围内的磨损行为,不具有普适性,对于磨损机理的理解还较为浅显。第2個阶段的磨损模型开始考虑物理过程和部分材料性能[8],将磨损过程中原子之间的相互作用考虑在内,能够定量描述某些材料属性对磨损行为的影响。第3阶段的磨损模型从材料的断裂、疲劳裂纹扩展等失效机制出发,根据经典弹塑性力学、断裂力学等理论设定破坏准则,从应力、应变的角度计算磨损的累积[14-15],能够宏观描述磨损机理。第4阶段的磨损模型从微观角度出发[16-18],考虑分子、原子尺度的相互作用,采用分子动力学来仿真小尺度粗糙峰的磨损过程,能够在一定程度上揭示磨损机理的本质。齿轮传动中,最常见的磨损形式为齿面黏着磨损与齿面疲劳磨损。
1.1 齿面黏着磨损数值建模研究
齿面黏着磨损是指啮合齿面间发生固相焊合作用后,黏着点在齿面相对滑动时被剪切断裂,金属材料由原齿面转移至相啮合齿面的材料去除行为,目前关于齿面黏着磨损研究大多基于Archard提出的黏着磨损公式[8,19]。1953年,Archard建立了多区域接触模型,考虑到磨屑形状和润滑状态的差异引入磨损系数,以表征接触时发生材料转移的概率,认为磨损是粗糙峰碰撞导致的块状材料去除行为,指出并不需要假设接触面积与磨粒尺寸的平均值为定值,形成了著名的Archard磨损公式,即
式中:[V]为磨损材料体积;[W]为法向载荷;[H]为软表面硬度;[K]为无量纲磨损系数;[s]为滑动距离。
Andersson[20]开创性地将Archard磨损公式引入直齿轮磨损计算中,并提出了著名的“单点观测法”。该方法假设在一个啮合周期内齿面上特定点P的压力是恒定的,首先,采用Hertz接触理论确定P点穿过齿轮作用线时的平均压力和接触宽度。然后,将齿轮的啮合过程等效为半径连续变化的一对圆柱体接触[21],推导了主、从动轮在啮合过程中的齿面滑动距离[sP,1]与[sP,2],基于Archard磨损模型计算得到P点的磨损深度[hP,n],即
式中:[aH]为赫兹接触半宽;[vP,1]和[vP,2]分别为2齿轮在啮合点处的切向速度;[hP,n]为经过[n]次积分循环后齿面上P点的磨损深度;[hP,(n-1)]为经过[n-1]次积分循环后P点的磨损深度;[pP,(n-1)]为P点穿过作用线时的平均压力;[sp]为P点相对啮合齿的滑动距离;[k]为常数。
作为齿轮黏着磨损模型研究的先行者,上述工作对于齿面磨损研究具有重要意义,但该理论并未考虑随着齿面磨损量的增加,齿面偏差与啮合载荷发生改变的问题。针对此不足,Flodin[11]基于Archard磨损公式,采用Winkler模型计算齿面接触压力,建立了直齿轮轻度磨损数值模型,规定每经过N次啮合进行一次齿面重构,从而将磨损过程对齿面接触的影响考虑在内。Flodin将式(3)改写为新的磨损计算公式
式中:[n]为当前积分循环次数;[Δt]为单次啮合离散后的时间步长;[N]为可认为齿面接触条件相同的啮合次数。
随后,Flodin等[22]将斜齿轮简化为多个沿轴线堆叠并依次旋转微小角度的薄片,将式(4)推广到斜齿轮齿面磨损计算中,Flodin并未考虑齿面粗糙度及润滑效应。Wu等[23]考虑低温热脱附磨损和高温氧化磨损行为,建立了齿轮混合润滑下的黏着磨损模型,将齿轮磨损研究推广至粗糙齿面,能够评估粗糙度及润滑特性对齿面磨损的影响。但该模型没有考虑磨损引起的齿廓改变,忽略了磨损对润滑状态和接触应力的影响。Wang等[24]基于修正Archard磨损模型[25],建立考虑润滑状态的齿面黏着磨损模型,将混合润滑下的黏着磨损研究推广至重载斜齿轮。
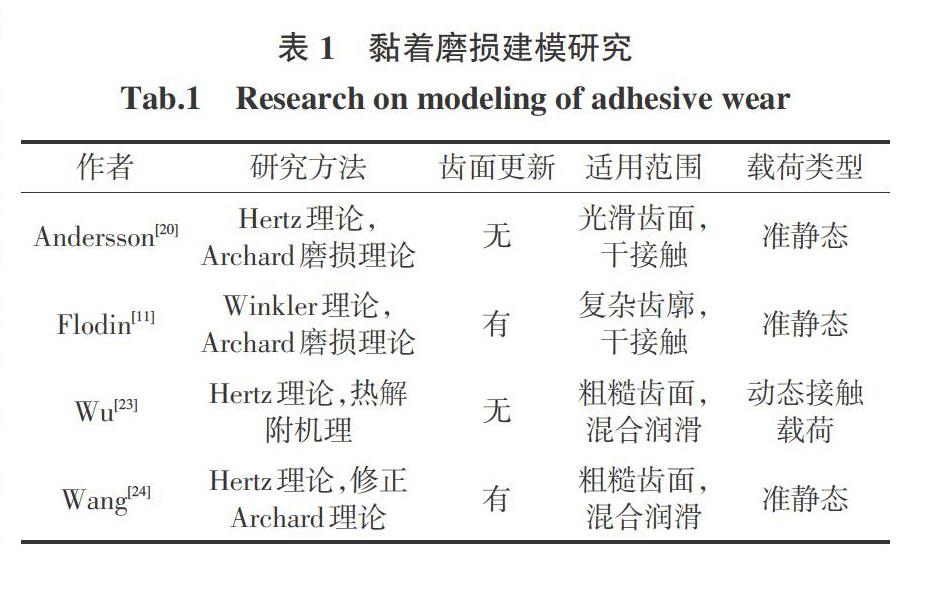
为总结提炼现有齿面黏着磨损模型建立相关研究的特点,将上述研究内容按照所采用的研究方法、有无齿面更新、适用范围和载荷类型4个方面进行提炼总结。从表1可以看出现有基于黏着磨损的齿面磨损建模研究多是基于Archard磨损公式,并假设齿轮副处于准静态工况的情况下开展的。磨损仿真大多沿着齿轮副的作用线进行,难以揭示特定啮合位置的磨损机理。啮合接触分析大多采用Hertz理论,即使考虑齿面粗糙度时也是如此,但Hertz理论的一个基本假设是理想光滑表面,因此,采用Hertz理论对粗糙表面进行接触分析的合理性值得探讨。虽然上述研究都精确地基于数学模型对齿面黏着磨损模型进行了建立,但仍存在考虑齿轮动力学特性不足,接触分析方法是否合理,磨损机理认识不够深入以及现有齿轮润滑理论分析与真实粗糙齿面润滑状态之间的差别等方面的研究缺陷。因此,齿面黏着磨损模型的建立仍需要进一步的研究。
1.2 齿面疲劳磨损数值建模研究
相关研究表明,正常工作条件下,齿轮的磨损形式主要为疲劳磨损[6,26]。齿轮在交变接触应力的作用下,齿面表层会产生塑性变形,在表层或次表层引起裂纹并不断扩大,造成剥落、点蚀和微点蚀等[27-29]。苏联的克拉盖尔斯基最先建立固体疲劳磨损理论,将其推广至齿轮传动、凸轮机构等多种摩擦副,基于该理论的齿轮疲劳磨损计算方法如下[30]。假设齿轮啮合时的接触范围为椭圆形,接触椭圆的长、短半轴分别为[a]和[b],则在滑动方向的赫兹接触半宽[B]为
Glode?等[31]提出了齿面疲劳磨损的断裂力学模型,采用有限元方法确定齿轮啮合时接触区域的应力场,推导应力强度因子与裂纹长度之间的函数关系,仿真了点蚀发生的疲劳过程,但未考虑润滑流体压力的影响。Fajdiga等[32]考虑润滑流体压力及残余应力对裂纹扩展的影响,基于虚拟裂纹伸展法建立了齿轮齿面接触疲劳的二维计算模型,采用有限元方法仿真初始裂纹萌生至形成表面微点蚀的疲劳过程,虽然该研究考虑了弹流润滑与切向的摩擦力,但缺乏对金属内部晶体结构的关注。Aslantas等[27]考虑内部晶相对齿轮疲劳磨损的影响,针对等温淬火球墨铸铁齿轮,基于有限元理论和线弹性断裂力学建立齿轮点蚀数值模型,指出借助现有标准试验数值即可对齿轮寿命进行仿真预测。上述模型多基于单一的疲劳磨损机理建立,但试验结果表明,单一的疲劳磨损模型会过量估计微点蚀的数量,难以准确预测齿轮磨损后的表面轮廓[33]。针对这一问题,Brand?o等[34-35]结合黏着磨损机理与疲劳磨损机理建立了齿面疲劳磨损模型,考虑了微凸体和润滑剂特性对磨损的影响,采用FZG齿轮试验台验证了该模型的准确性。Liu等[36]考虑界面特性、材料参数、磨损演变等多种因素的耦合作用,建立了综合考虑机械性能的齿轮接触疲劳模型,用以解释混合弹流下齿面疲劳失效模式的竞争机制。近年来,同时考虑轻微磨损与接触疲劳失效的研究方法正形成一种新的趋势[33-37]。
2.3 考慮微观形貌演变的齿面磨损仿真研究
齿轮磨损问题影响因素较多,精确建模的工作量和计算量都非常巨大,因此现有研究都对磨损问题进行了简化。尤其精确的微凸体建模及力学分析是非常复杂的,因此已有研究大多忽略了微凸体碰撞的动态力,假设滑动力是导致摩擦表面产生微裂纹的唯一因素。然而,忽略磨损中表面形貌对次表面应力的影响,可能降低磨损预测的精度[37]。一些学者开始对齿轮磨损中表面形貌的演变开展研究,结合磨损模型进行齿轮磨损预测,以提高磨损计算的准确性。
Greenwood等[53]基于微凸体的弹塑性提出了粗糙表面的接触模型(GW模型),研究表明GW模型能较好地模拟两粗糙表面的接触,且不存在明显的精度损失。该模型假设接触表面覆盖有类球状微凸体,考虑微凸体的弹性和塑性两种变形机理,推导得到典型高斯分布的粗糙表面的接触面积[A]为
式中:[η1]为微凸体密度;[β1]为微凸体峰顶的曲率半径;[σp1]为微凸体高度的标准差;[Aap]为表观接触面积;[F1]为积分函数;[h]为粗糙峰高度与峰顶平均高度间的标准化距离。
Morales-Espejel等[54]考虑弹流润滑接触过程中,微观几何、磨损系数与接触压力的变化,基于微观几何混合润滑模型[55]建立表面形貌演变的预测模型,研究表面疲劳和轻度磨损对微点蚀的共同作用。Guilbault等[37]从统计学角度出发,考虑磨损和承载下的塑性变形对粗糙峰的影响,建立磨损过程中表面形貌演变的随机模型,并推广至齿轮轻微磨损预测与接触疲劳分析,采用试验方法进行了验证。Liu等[36]考虑界面特性、材料参数等多种因素的耦合作用,建立了综合考虑机械性能的齿轮接触疲劳模型,考虑初始表面粗糙度对齿面磨损展开研究。
与磨损的四大基本类型相比,关于磨损过程中表面形貌演变的数值研究较少,大多采用试验方法。由于粗糙表面精确建模的复杂性以及精确计算的高难度,目前,关于齿轮磨损表面形貌的研究主要应用随机过程理论和统计学原理。随着对齿轮摩擦磨损问题研究的进一步深入,逐渐揭示了表面形貌对齿轮润滑、接触应力及齿面磨损等问题的影响作用,对表面形貌演变开展研究的重要性逐渐凸显。
3 结论与展望
在简要介绍了齿轮齿面磨损概况的基础上,对齿面磨损数值建模研究及数值仿真展开了论述。现有齿面磨损数值建模研究及数值仿真虽然在方法上取得了一定的研究成果,但齿面磨损参量众多,系统动态特性、润滑状态等较为复杂,仍存在一些问题值得深入探索。结合本文的分析,齿面磨损数值建模研究及数值仿真在以下几方面还需要展开深入研究。
1)齿轮磨损通常为多种磨损机理的复合作用,其磨损过程也很难用单一的磨损模型表征。目前的齿轮磨损模型仍然具有局限性。考虑更加全面的磨损类型,深入挖掘齿面磨损中不同磨损机理的复合作用,建立纳入多种磨损机理的齿面磨损模型,为齿面磨损数值仿真提供工作基础。
2)齿轮系统是一个涉及齿轮动力学、齿轮润滑、表面形貌与齿面磨损的多变量耦合系统。考虑齿轮的多种润滑状态和润滑介质、齿轮副系统动态响应和齿面磨损之间的相互作用,量化各个参量对齿面磨损的影响作用,对指导齿轮的设计和使用阶段,提高齿轮的工作寿命具有重要意义。
3)由于对磨损机理认识不够完善,以及对润滑剂性质退化、粗糙度变化等时变参数考虑不足,单纯采用数值仿真预测齿面磨损,尤其是长周期下的齿面磨损预测可能会偏离实际。将齿轮磨损的数值仿真与试验方法相结合,基于实际测得的齿轮副系统动态响应、磨损量、表面硬度、润滑油杂质等参数,随磨损进程调整、更新齿面磨损模型,提高齿轮寿命的预测精度。
4)齿轮系统的动态特性、润滑状态会随磨损进程发生改变,同时其动态接触载荷、加工尺寸等参数具有不确定性和随机性,齿面磨损也是具有统计特征的随机过程。建立齿轮磨损随机过程的基本模型,进行齿轮寿命与系统可靠性预测,研究齿轮磨损可靠性为齿轮磨损研究提供了另一种思路。
参考文献:
[1] ROKICKI P,KOZIK B,BUDZIK G,et al. Manufacturing of aircraft engine transmission gear with SLS (DMLS) method[J]. Aircraft Engineering and Aerospace Technology,2016,88(3):397-403.
[2] BAKSHI S,DHILLON P,MARUVADA T. Design and optimization of planetary gearbox for a formula student vehicle[J]. SAE International Journal of Materials and Manufacturing,2014,7(3):688-697.
[3] ZHANG L X,LIU S R,LI W L,et al. Reliability analysis on gearbox transmission system of agricultural machinery chassis based on FTA[J]. Advanced Materials Research,2013,694/695/696/697:876-882.
[4] STAICU S. Planetary gear train for robotics[C]//IEEE International Conference on Mechatronics,ICM/HIMA 2005. Taipei,DOI:10. 1109/ICMECH. 2005. 1529371:840-845.
[5] WU S,CHENG H S. A friction model of partial-EHL contacts and its application to power loss in spur gears[J]. Tribology Transactions,1991,34(3):398-407.
[6] CHOY F K,POLYSHCHUK V,ZAKRAJSEK J J,et al. Analysis of the effects of surface pitting and wear on the vibration of a gear transmission system[J]. Tribology International,1996,29(1):77-83.
[7] LIU G,PARKER R G. Impact of tooth friction and its bending effect on gear dynamics[J]. Journal of Sound and Vibration,2009,320(4/5):1039-1063.
[8] ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of Applied Physics,1953,24(8):981-988.
[9] BOSMAN R,SCHIPPER D J. Mild wear prediction of boundary-lubricated contacts[J]. Tribology Letters,2011,42(2):169-178.
[10] 張俊,卞世元,鲁庆,等. 准静态工况下渐开线直齿轮齿面磨损建模与分析[J]. 机械工程学报,2017,53(5):136-145.
[11] FLODIN A,ANDERSSON S. Simulation of mild wear in spur gears[J]. Wear,1997,207(1/2):16-23.
[12] HUANG D Q,WANG Z H,KUBO A. Hypoid gear integrated wear model and experimental verification design and test[J]. International Journal of Mechanical Sciences,2020,166:105228.
[13] RHEE S K. Wear equation for polymers sliding against metal surfaces[J]. Wear,1970,16(6):431-445.
[14] KAPOOR A,FRANKLIN F J. Tribological layers and the wear of ductile materials[J]. Wear,2000,245(1/2):204-215.
[15] FRANKLIN F J,WIDIYARTA I,KAPOOR A. Computer simulation of wear and rolling contact fatigue[J]. Wear,2001,251(1/2/3/4/5/6/7/8/9/10/11/12):949-955.
[16] AGHABABAEI R,WARNER D H,MOLINARI J F. Critical length scale controls adhesive wear mechanisms[J]. Nature Communications,2016,7:11816.
[17] AGHABABAEI R,BRINK T,MOLINARI J F. Asperity-level origins of transition from mild to severe wear[J]. Physical Review Letters,2018,120(18):186105.
[18] MOLINARI J F,AGHABABAEI R,BRINK T,et al. Adhesive wear mechanisms uncovered by atomistic simulations[J]. Friction,2018,6(3):245-259.
[19] FENG K,BORGHESANI P,SMITH W A,et al. Vibration-based updating of wear prediction for spur gears[J]. Wear,2019,426/427:1410-1415.
[20] ANDERSON S,SERIKSSON B. Prediction of the sliding wear of spur gears[C]//Proceedings of the Fourth Nordic Symposium on Tribology. Denmark: Nordtrib′90, 1990:10-13.
[21] ANDERSSON S. Partial EHD theory and initial wear of gears[D]. Stockholm,Sweden:Royal Institute of Technology,1975.
[22] FLODIN A,ANDERSSON S. Simulation of mild wear in helical gears[J]. Wear,2000,241(2):123-128.
[23] WU S F,CHENG H S. Sliding wear calculation in spur gears[J]. Journal of Tribology,1993,115(3):493-500.
[24] WANG H B,ZHOU C J,LEI Y Y,et al. An adhesive wear model for helical gears in line-contact mixed elastohydrodynamic lubrication[J]. Wear,2019,426:896-909.
[25] MASJEDI M,KHONSARI M M. An engineering approach for rapid evaluation of traction coefficient and wear in mixed EHL[J]. Tribology International,2015,92:184-190.
[26] XU X,LAI J,LOHMANN C,et al. A model to predict initiation and propagation of micro-pitting on tooth flanks of spur gears[J]. International Journal of Fatigue,2019,122:106-115.
[27] ASLANTA? K,TA?GETIREN S. A study of spur gear pitting formation and life prediction[J]. Wear,2004,257(11):1167-1175.
[28] CARDOSO N F R,MARTINS R C,SEABRA J H O,et al. Micropitting performance of nitrided steel gears lubricated with mineral and ester oils[J]. Tribology International,2009,42(1):77-87.
[29] WEIBRING M,GONDECKI L,TENBERGE P. Simulation of fatigue failure on tooth flanks in consideration of pitting initiation and growth[J]. Tribology International,2019,131:299-307.
[30] 王淑仁,閆玉涛,殷伟俐,等. 齿轮啮合摩擦疲劳磨损的计算模型[J]. 东北大学学报(自然科学版),2008,29(8):1164-1167.
[31] GLODE? S,WINTER H,ST?WE H. A fracture mechanics model for the wear of gear flanks by pitting[J]. Wear,1997,208(1/2):177-183.
[32] FAJDIGA G,FLA?KER J,GLODE? S,et al. Numerical modelling of micro-pitting of gear teeth flanks[J]. Fatigue & Fracture of Engineering Materials & Structures,2003,26(12):1135-1143.
[33] BRAND?O J A,MARTINS R,SEABRA J H O,et al. Calculation of gear tooth flank surface wear during an FZG micropitting test[J]. Wear,2014,311(1/2):31-39.
[34] BRAND?O J A,MARTINS R,SEABRA J H O,et al. An approach to the simulation of concurrent gear micropitting and mild wear[J]. Wear,2015,324-325:64-73.
[35] BRAND?O J A,SEABRA J H O,CASTRO J. Surface initiated tooth flank damage[J]. Wear,2010,268(1/2):1-12.
[36] LIU H L,LIU H J,ZHU C C,et al. Study on gear contact fatigue failure competition mechanism considering tooth wear evolution[J]. Tribology International,2020,147:106277.
[37] GUILBAULT R,LALONDE S. A stochastic prediction of roughness evolution in dynamic contact modelling applied to gear mild wear and contact fatigue[J]. Tribology International,2019,140:105854.
[38] YANG Y,CAO L Y,LI H,et al. Nonlinear dynamic response of a spur gear pair based on the modeling of periodic mesh stiffness and static transmission error[J]. Applied Mathematical Modelling,2019,72:444-469.
[39] BAJPAI P,KAHRAMAN A,ANDERSON N E. A surface wear prediction methodology for parallel-axis gear pairs[J]. Journal of Tribology,2004,126(3):597-605.
[40] LUNDVALL O,KLARBRING A. Simulation of wear by use of a nonsmooth Newton method:a spur gear application1-2*[J]. Mechanics of Structures and Machines,2001,29(2):223-238.
[41] PARK D,KAHRAMAN A. A surface wear model for hypoid gear pairs[J]. Wear,2009,267(9/10):1595-1604.
[42] KUANG J H,LIN A D. The effect of tooth wear on the vibration spectrum of a spur gear pair[J]. Journal of Vibration and Acoustics,2001,123(3):311-317.
[43] WOJNAROWSKI J,ONISHCHENKO V. Tooth wear effects on spur gear dynamics[J]. Mechanism and Machine Theory,2003,38(2):161-178.
[44] DING H L,KAHRAMAN A. Interactions between nonlinear spur gear dynamics and surface wear[J]. Journal of Sound and Vibration,2007,307(3/4/5):662-679.
[45] LIN A D,KUANG J H. Dynamic interaction between contact loads and tooth wear of engaged plastic gear pairs[J]. International Journal of Mechanical Sciences,2008,50(2):205-213.
[46] WANG W,WONG P L,GUO F. Application of partial elastohydrodynamic lubrication analysis in dynamic wear study for running-in[J]. Wear,2004,257(7/8):823-832.
[47] JOHNSON K L,GREENWOOD J A,POON S Y. A simple theory of asperity contact in elastohydro-dynamic lubrication[J]. Wear,1972,19(1):91-108.
[48] AKBARZADEH S,KHONSARI M M. Prediction of steady state adhesive wear in spur gears using the EHL load sharing concept[J]. Journal of Tribology,2009,131(2): DOI:10. 1115/1. 3075859.
[49] MASJEDI M,KHONSARI M M. Film thickness and asperity load formulas for line-contact elastohydrodynamic lubrication with provision for surface roughness[J]. Journal of Tribology,2012,134(1): DOI:10. 1115/1. 4005514.
[50] MASJEDI M,KHONSARI M M. Mixed elastohydrodynamic lubrication line-contact formulas with different surface patterns[J]. Journal of Engineering Tribology,2014,228(8):849-859.
[51] MASJEDI M,KHONSARI M M. On the prediction of steady-state wear rate in spur gears[J]. Wear,2015,342:234-243.
[52] 徐宏海,谢雄伟,关通. RV减速器国产化批量制造关键问题探讨[J]. 机械传动,2018,42(10):171-174.
[53] GREENWOOD J A,TRIPP J H. The contact of two nominally flat rough surfaces[J]. Proceedings of the Institution of Mechanical Engineers,1970,185(1):625-633.
[54] MORALES-ESPEJEL G E,BRIZMER V,PIRAS E. Roughness evolution in mixed lubrication condition due to mild wear[J]. Journal of Engineering Tribology,2015,229(11):1330-1346.
[55] MORALES-ESPEJEL G E,WEMEKAMP A,F?LIX-QUI?ONEZ A. Micro-geometry effects on the sliding friction transition in elastohydrodynamic lubrication[J]. Journal of Engineering Tribology,2010,224(7):621-637.
[責任编辑 杨 屹]
