问题链驱动：知识从“解构”走向“重构”

丁洪 洪荟春

[摘要]问题链侧重情境的完整性、结构的逻辑性和衔接的关联性。知识的学术形态需要转化成教育形态的问题链，以演绎知识解构到重构的关键环节和智慧路径，驱动学生理解知识的本质，并最终超越具体知识，内化关键能力，丰盈理性精神。

[关键词]问题链;问题驱动;知识解构;模型重构;数学化

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0007-04

数学知识存在两种形态，即学术形态和教育形态。教材呈现的数学知识追求“准确的定义、逻辑的演绎和严密的推理”，这是知识的学术形态，偏重线性编排和形式化。教学中引导学生经历知识的“再创造”过程，激发学生用“火热的思考”去理解数学知识“冰冷的美丽”，这是知识的教育形态，注重个性建构和数学化。教师的任务就是把知识的学术形态转化为教育形态。那么，转化的路径是什么？转化过程要遵循哪些原则？转化的效果又该如何评估？接下来，以苏教版六年级下册第5单元“用方向和距离确定位置”磨课为例，谈谈这方面的收获和体会。

一、第一次执教：解读静态知识

1.教学设想

从联系的角度看，学生已经学习了四面八方、数对确定位置、角的认识和比例尺的意义及其应用。作为小学阶段最后一次确定位置的主题学习，需要学生有效调用、合理支撑和适当对比已有概念，进而渗透极坐标的思想模型，适时发展学生的空间观念。基于这样的分析，笔者决定充分用好主题图，根据教材提供的问题链，引领学生有效经历确定位置的具体过程，进而把握规律和建构模型。

2.教学设计

首先，以确定灯塔1和灯塔2相对于轮船的位置问题引入，驱动学生对问题进行简单表征，并激发学生对具体表征进行反思;其次，介绍方向重新约定的基准对象和表达方式，并适时出示相关角度，驱动学生合理、完整和具体地表示灯塔的位置;接着，用问题驱动学生比较所确定位置的异同，侧面凸显用方向和距离确定位置的特点;最后，通过针对性的练习，理解内化确定位置的方法模型。以下是四个主要教学环节：

（1）创设情境，激趣导入

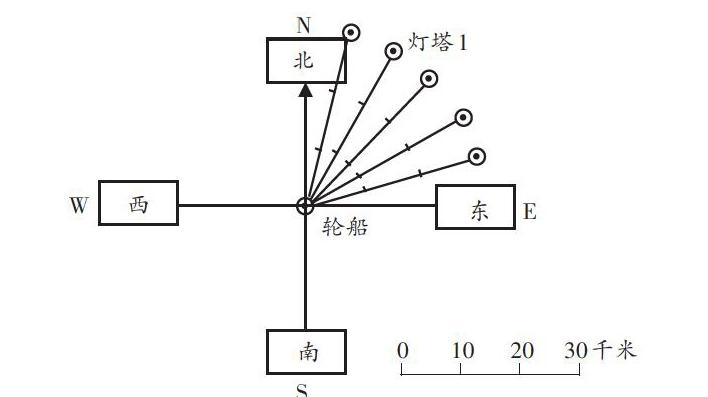
师（出示主题图）：一艘轮船向正北方向行驶，你能说出灯塔1和灯塔2分别在轮船的什么方向吗？

生1：灯塔1在轮船的东北方向。

生2：燈塔2在轮船的西北方向。

师：你觉得这样表达具体吗？今天这节课我们就来研究确定位置的新方法。

（2）介绍规则，约定表达

师（出示指南针）：人们常用指南针测定方向，指南针指向正北和正南，如果物体不在南北线上，就要看它的位置相对于北或南是偏东还是偏西。因此，东北方向也叫作北偏东，西北方向也叫作北偏西。以此类推，你会说东南方向和西南方向吗？

师：现在，你能说说灯塔1和灯塔2各在轮船的什么方向吗？

（3）完整表达，建构模型

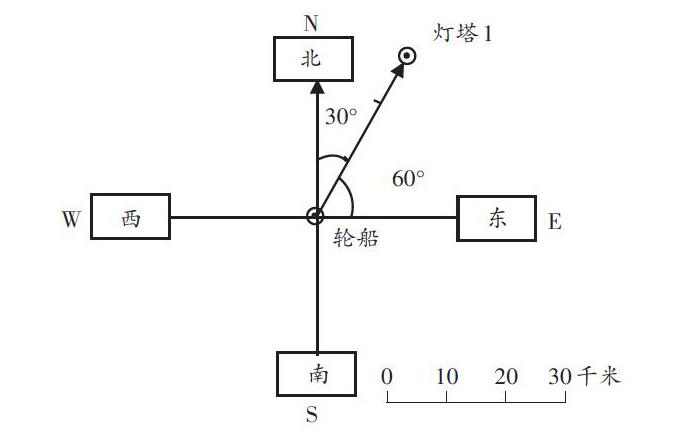
师（出示平面图）：如果把物体抽象成点，用点的位置表示物体的位置，你能理解图中标出的30。吗？现在你能完整表达灯塔1的位置并填空吗？

师：你是怎样确定距离30千米的？

师：像这样确定位置，我们称之为用方向和距离确定位置。我们以前学过哪些确定位置的方法？现在又有了哪些新的认识？（课件配合演示）

（4）实践运用，理解内化（略）

3.教学反思

纵观全课，教学使用了教材给定的情境，但是这些情境远离学生实际，激发不了学生确定位置的内在需求;教学紧扣“调用经验模糊确定、整合新知精准确定和对比反思内化模型”的问题链，但是精当的讲解未能引发学生知识的自然生长，缺少过程的搬运难以激发学生对知识存在价值的正向体验;教学中的练习题来自教材，但是机械的解决未能催生学生关键能力的形成。怎么办？首先，需要寻找与灯塔相关的图片或视频，弥补静态情境呈现的留白和不足，变“要我确定位置”为“我要确定位置”;其次，需要再次确认教学的重心，引导学生经历知识生长的关键环节，使“平均用力”变为“难点突破”;最后，需要对练习进行有机整合和梯度呈现，帮助学生消化知识和建构模型，从“举三反一”到“举一反三”。这样处理有助于教师“有生长”地教，帮助学生“有过程”地学。

二、第二次执教：指向生长需要

1.目标定位

基于以上实践和反思，通过研读教材、前测调查和持续学习，我们弄清楚了学生的学习起点是二年级的用“四面八方”模糊确定位置，而现在要精准定位两个物体之间的位置，即需要重新“改造”方位的描述，也就是适时引入角度（这是教学的重难点），需要确认两点之间的距离，借助比例尺加以计算，最后还需要比较不同确定位置模型的相同点和不同点，感悟知识的独特地位和价值魅力。也就是说，教学源自实际生活的需要、知识生长的需要和思维发展的需要。为此，教学的目标定位在情境要真实“可亲近”、过程要经历“再创造”，而比较则要紧扣“问题情境和数学本质”。

2.教学实践

首先，出示灯塔的图片，让学生调用生活经验猜猜“它是谁”，再播放一段介绍灯塔的视频，拉近学生与灯塔的距离，使学生了解灯塔具有的确定位置的功能。紧接着创设情境：“一艘轮船向正北方向行驶，天气突然变得恶劣，视线变得模糊，安全航行急需要确定位置，好在前方出现了——灯塔。”然后顺势抛出问题：“如果你是船长，以轮船作为观测点，你能确定灯塔1在轮船的什么位置吗？”并将物体抽象成数学的点，用点的位置表示物体的位置，设置一个完整的探究活动。

其次，锁定出现频率最多的“东北方向”和"30千米”。先引导学生反思“你是怎样确定距离30千米的？”，回顾运用比例尺和图上距离求解实际距离的方法;再引导学生思考“只说在东北方向，你觉得具体吗？”，激发学生对具体问题表征的探究，引出角度的表达;然后同时给出30°和60°，让学生尝试描述“北偏东30°”和“东偏北60°”，引发方向描述起点的讨论，促使学生调用生活经验和已有知识理解以“正北和正南”作基准的科学性、合理性和现实性，能够将“东北方向”换个角度重新描述成“北偏东”，并此类推到其他方位的重新约定;最后将关键信息“北偏东30°”和“30千米”一起出示，让学生组合信息，并追问组合的内在依据。

生2：复活岛在轮船的南偏西20°方向60千米处。

生3：我来纠错，应该是南偏西70°。

师：你能说服他吗？

生3：西偏南20°就是南偏西70°，要用90°-20°=70°。

师：心中有标准，做事有分寸。

【思考：问题链一般包含正向迁移和反向审视两种类型。教学中，灯塔2的位置确定是知识的正向迁移，而对复活岛的20°方向的辨析属于方法的反向审视。一般而言，反向审视练习主要针对关键环节和关键方法，因为其特殊的地位和意义，所以需要反复、多角度和立体化的锤炼。就教育的目的性而言，两者互为补充、共同作用，服务于“南北作基准”的方法建构。】

【教学片段3】对比概括，内化模型

（1）猜中概括确定位置的路径

师（出示“南偏东”）：这里是要猜神秘岛的位置，请看好提示。现在你能确定什么？

生1：能确定南偏东这一个区域。

师（出示“80°”）：现在你又能确定什么？

生1（边说边指）：能确定一条线，神秘岛应该在这条线上。

师：还有什么就能确定神秘岛的具体位置？

生1：距离。

师：给出距离“50千米”，你能确定吗？

生1：这里1厘米表示10千米，所以我比画了5次，神秘岛大约在这个点。（图略）

师：恭喜你！面一线一点，范围不断缩小，直到最后确定。

（2）调中感知位置关系的相对

师：轮船在灯塔1的什么位置？

生2：轮船在灯塔1南偏西30°方向30千米处。

师：改变观测点，通过观测灯塔1在轮船什么位置，你发现了什么？

生3：方向相反，但角度和距离都相等。

师：你能介绍一下小组长相对于你的位置吗？

生4：小组长在我前面大约2米的地方。

生5：某某同学在我后面大约2米的地方。

师：比较这两位同学的说法，你有什么发现？

生（齐）：方向相反，距离相同。

（3）比中突出不同方法的关联

师（出示课件）：这两个点都被确定位置了，两种确定位置的方法有什么相同点和不同点？

生6：左边用的是行和列，右边用的是方向和距离。

生7：左边确定的是教室里某个人的位置，而右边确定的是两个物体之间的位置。

师：如果顺着这个思路，左边凸显的是整体中的点的位置，而右边凸显的是点与点之间的位置，适用的环境不一样。你还能举一些例子吗？

生8：围棋中的棋子、汽车中的座位……这些与数对确定位置差不多。

生9：像如皋和海门，两个地方之间的位置确定更适合方向和距离。

师：真棒！其实，梳理不同点，也就间接回答了今天学习的重要性。接下来，说说相同点。

生10：都要考虑两个因素。

生11：还要约定先后顺序。

师：是的，以前需要锁定关键信息和约定表达方式，今天也是，将来还是。

【思考：問题链想要“链”出精彩，就必须借助对比，驱动学生的学习深入浅出。首先，一步一景式的猜测和概括，助推学生玩中不断思考，尤其是抽象出两点之间确定位置的路径时，使得学习从“特殊”走向“一般”;接着，对比因调整观测点带来的位置描述的变化，初步得到“方向相反，角度和距离不变”的结论，当进一步互动唤醒学生原有认知时，位置相对性的特征呼之欲出，使得一般结论贯通“已知”和“未知”;最后，横向比较两种典型的“确定位置”，在不同点中感知确定方法和适用情境的差异性，在相同点中触摸确定方法和内在本质的一致性，使得数学与生活的联系以及数学自身的发展从“模糊”走向“清晰”。】

【总评】至此，我们找到了学术形态转化成教育形态的数学化路径，即将零散的、模糊的和机械的问题点有机整合成相对系统的、清晰的和灵动的问题链，通过点的有效突破、层层递进和建构完善，驱动学生经历知识生长的全过程，这是从设计的层面为知识的重构做好了铺垫。对于转化过程遵循的原则，笔者认为不但要做到情境的完整性、结构的逻辑性和衔接的关联性，还要做到情境设置服务学习内容、结构编排遵循认知规律和衔接紧扣生长节奏，这些是从策略层面为知识的重构保驾护航。转化的效果又该如何评估呢？从学的角度看，主要观察学生是否经历心动想学、生动表征和灵动内化的过程。从教的角度看，主要考量教师所处的教学境界，第一种是简单地将教材中的知识搬运给学生，教出于传授的本能;第二种是针对知识本身，引入媒体手段、方法技巧和资料补充等，教展现解惑的本领;第三种是基于知识的本质理解，教学演绎知识解构到重构的关键环节和智慧路径，并最终超越具体知识，驱动学生内化关键能力和丰盈理性精神。