类比提升 自主建构——“空间向量及其线性运算”教学实践与反思

董逸婷

(江苏省苏州实验中学，215011)

本节课的教学内容选自《普通高中课程标准实验教科书·数学(选修2-1)》(苏教版)第3章第1节“空间向量及线性运算”.

向量是既有大小又有方向的量,既能像数一样进行运算,本身又是一个“图形”.向量是近代数学中重要和基本的概念之一,是沟通代数、几何与三角函数的桥梁,在很多知识中有重要的应用．本章要学习的空间向量将为解决三维空间中图形的位置关系与度量问题提供一个十分有效的工具，为处理立体几何问题提供了新的视角.本课作为章节的起始课,是学生在学习了平面向量的基础上展开的,经历了向量及其运算由平面向空间推广的过程,既复习巩固了平面向量的有关内容,又为后面用向量解决立体几何问题做好铺垫,起到承前启后的作用．教学过程中应充分让学生类比猜想、自主探索,得出相应的法则和性质,引导学生主动学习类比、归纳、推广、化归等思想方法,提高数学素养.

一、教学过程片段实录

1. 创设情境,问题导入

问题国庆期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观赏黄浦江,然后抵达东方明珠(B)游玩,如图1,游客的实际位移是什么?可以用什么数学概念来表示这个过程?

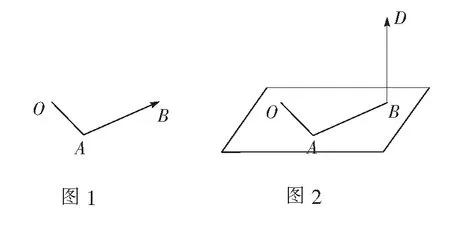
①

师追问:如果游客还要登上东方明珠顶端(D)俯瞰上海美丽的夜景,如图2,那它实际发生的位移是什么?又如何表示呢?

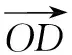
②

师:比较① ②,都是向量关系式,背景有何不同?

师:非常好,这就是这节课我们要学习研究的主要内容——空间向量及其线性运算.

评注图1中的引入情境,于学生而言,非常熟悉．课堂上追问学生,若登顶东方明珠D又该如何表示,既贴近学生生活实际又自然将平面向量拓展到空间向量,既揭示了学习空间向量的必要性,又激发了学生的学习兴趣,也为后续空间向量的加法运算做了铺垫(尤其是在验证空间向量的加法结合律)．

2.类比平面,提炼概括

师:高一我们已经系统研究过平面向量,同学们可以回忆一下,什么是平面向量?平面向量主要研究哪些内容?

生:平面上既有大小,又有方向的量叫做平面向量．我们主要研究了平面向量的概念、线性运算、数量积及其应用．

师:非常好,我们从以上方面研究了平面向量(PPT给出图3知识框架)．

师：今天,我们从二维平面推广至三维空间．首先,从概念出发.请同学们复习回顾平面向量相关知识,并阅读课本,整理提炼空间向量有关概念,填写讲义上的表1.

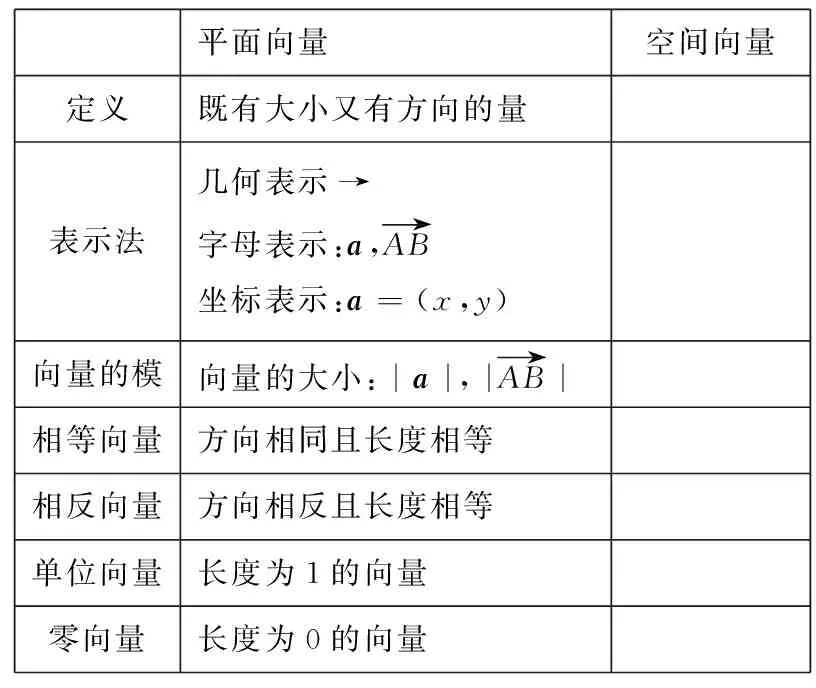
表1空间向量基本概念

师:通过阅读填表,请同学们概括一下空间向量概念的主要内容是什么?对于空间向量的学习有没有受到学习方法上的启发?

生:空间向量的概念与平面概念是完全一致的．对于学习方法,我觉得可以类比平面向量来学习．

师:非常好,这位同学既概括了知识又获得了方法．既然空间向量与平面向量的概念完全一致,那么空间向量和平面向量有什么联系呢?下面我们一起来看一下投影上的探究．

3.探究

探究1空间任意任意两个向量是否可以异面?

生:空间任意两个向量都是共面向量,因为它们可以平移至同一平面．

师:很好,所以凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们．(PPT动态演示平移过程)

评注学生对平面向量的知识结构已经比较了解,空间向量的知识结构和它有很多的相似性,与其再次由教师喋喋不休地重复,不如让学生自己去阅读、比较、辨别、思悟,在类比中生成,在生成中提升.

4.跳出平面,明确概念

练习1给出以下命题:

① 两个空间向量相等,则它们的起点、终点相同;

② 若空间向量a和b满足|a|=|b|，则a=b;

③ 空间中任意两个单位向量必相等;

④ 空间任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量．

其中正确命题的个数是______.

生:正确命题个数是1个．① ② 错,两个向量相等需要方向相同、长度相等;③ 方向可以不同；④ 正确．

评注此环节的设计,以题目形式出现,第一，让学生明确空间向量的基本概念和平面向量是一样的,让学生在不知不觉中“跳出平面,进入空间”;第二，对于跟踪练习的第4个问题，是下面在运算法则和运算律类比中非常重要的一个结论,高中阶段学习的向量是“自由向量”,所以任意两个空间向量都可以“平移”到同一个平面内.之所以没有单独拿出来思考,是因为想让学生在不知不觉中完成平面向量到空间向量的思维跨越,同时也自然衔接到下面的类比．

5.交流合作 运算类比

师:研究了空间向量基本概念之后类比平面向量,我们还要研究它的线性运算.平面向量的线性运算和性质在空间向量仍然适用吗?(用PPT给出表格2)

表2 线性运算法则的类比

生:一样的,加法用三角形法则和平行四边形法则,减法用三角形法则.

师:非常好,所以在空间向量线性运算中,平面向量的法则仍然适合.(PPT演示复习运算法则)

师:空间向量的结合律呢?结合律涉及3个向量的关系.还适用吗?

探究2空间向量的加法是否满足结合律?

(实物投影学生的合作探究结果,如图4)

师:我们发现空间向量线性运算的法则和运算律也和平面向量完全一致.

评注学生明确了任意两个空间向量都可以“平移”到同一个平面内的结论后,那么涉及两个空间向量的运算法则和运算律的问题,显而易见是可以平稳对接的．可以借助引例中的图2,让同桌二人分工协作,一个用图形求左边的向量,一个求右边的向量,很轻松地验证成功.同时让学生把两个图放到一起就看出了四面体这个空间几何体,又一次跳出平面,跨入了空间．

6.类比提升 定理推广

师:到目前为止,我们已经把知识从平面推广到了空间．同学们还记得平面中一种特殊的向量——共线(平行)向量吗?它可以推广到空间吗?平面向量共线定理在空间中仍然成立吗?

(学生回答共线(平行)向量定义、记法、一个规定、共线向量定理)

练习2

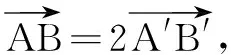
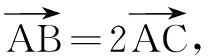
评注通过共线定理在空间向量中的运用,复习回顾平面向量中的运用,有助于对知识的有机整合.

7.例题评析 数学应用

例1已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量．(如图5)

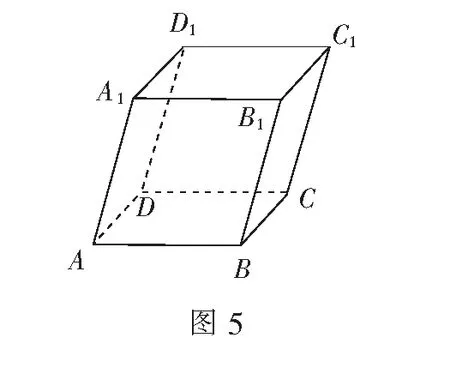
评注例题的作用与价值旨在帮助学生熟练空间向量的线性运算法则,借助几何体加强学生对空间向量的直观感知.在运算过程中,提炼蕴含其中的数学思想“空间问题平面化”.第(2)小题中,总结出“平行六面体”法则,即始点相同的三个不共面向量之和,等于以这三个向量的棱的平行六面体的以公共始点为始点的对角线所示向量.为后续空间向量基本定理及正交分解做准备.

8.课堂小结(略)

二、教学后记

1.精心预设,以问题为教学线索

问题是数学的心脏.本课的教学设计以问题的解决为线索,在教师引导下,使学生的思维从问题开始,由问题深化.自然而又不突兀地引出了本课的学习内容——空间向量.例题既巩固了空间向量线性运算的法则和运算律,又引出了“空间平行六面体法则”,为下节课空间向量基本定理做了铺垫.课堂始终以数学问题为载体,以教师的“导”为主线,以学生的“学”为标的,教师和学生通过数学问题这一课堂载体形成双向交流和互动对话,互相促进,教学相长.

2.知识生长,以类比为教学方法

引导学生用类比的学习方法来探究空间向量的相关知识.在类比中生成空间向量的概念、运算法则、运算律相关知识.既巩固了平面向量,又将知识由二维推广至三维,由平面推广至空间.类比是本课的主要思想方法,同时在教学过程中,笔者也有意识地渗透转化与化归、数形结合等思想.在例题讲解过程中,引导从不同角度用不同方法解决问题,加入变式训练,训练逆向思维能力、化归转化能力,培养学生的数学素养.

3.自主构建,以学生为课堂主体

教学的过程不是将知识从一个容器导入另一个容器的过程.我们要重视学生的课堂自主参与性,重视学生课堂探究能力和创新能力的培养.激励学生积极思维,大胆思索,勇敢实践.