3维卷积递归神经网络的高光谱图像分类方法

关世豪，杨 桄，李 豪，付严宇

（空军航空大学，长春130022）

引 言

高光谱遥感图像是机载或星载的成像光谱仪在电磁波谱的紫外、可见光、近红外和中红外区域，以数十至数百个连续且细分的光谱波段对地面目标区域同时成像，得到的以像素为单位的高光谱图像［1］，可同时获取地物空间信息与高分辨率的光谱信息。凭借其丰富的光谱信息，高光谱遥感图像为人们研究地表物体的性质，尤其是对地物的精细分类和识别提供了依据，在农业［2］、林业［3］、采矿业［4］、城市规划［5］、国防建设［6］以及空间探索［7］等方面应用广泛。

卷积神经网络（convolutional neural network，CNN）是计算机视觉领域占主流地位的一种深度学习网络，也是目前在高光谱图像分类领域应用最广泛的深度学习网络。HU等人［8］首次采用1维卷积神经网络（onedimensional convolutional neural network，1-D-CNN）实现了基于光谱特征的高光谱图像分类。YANG等人［9］分别利用1-D-CNN与2维卷积神经网络（two-dimensional convolutional neural network，2-D-CNN）从高光谱数据中提取光谱特征与空间特征，将两种特征串接后通过分类器完成分类，但这种将光谱与空间特征分开提取的方法需要复杂的预处理，破坏了高光谱数据的3维结构。近几年来，研究者将3维卷积神经网络（three-dimensional convolutional neural network，3-DCNN）应用到高光谱图像分类中［10-11］，此类方法无需复杂的预处理和后处理，可以在不破坏高光谱图像数据结构的前提下，直接提取空谱联合特征进行分类，在实际分类中表现出较好的分类效果。

高光谱图像光谱分辨率高，相邻波段之间具有高度相关性，在非相邻波段上也表现出一定的相关性［12］，其光谱数据本质上是一类序列数据。当前基于CNN的高光谱图像分类方法都是将单个像元上的光谱数据看作是无序的高维向量［13］，这不符合光谱数据的特性。对于序列数据而言，循环神经网络（recurrent neural network，RNN）是最自然的神经网络架构，因此，研究者考虑利用RNN对高光谱图像分类。MOU等人［14］首次将RNN应用于高光谱图像分类中，与支持向量机（support vector machine，SVM）和1-D-CNN等方法相比，该方法达到了更高的分类精度，这也间接证明了RNN在提取光谱特征的性能要优于CNN。但是这种方法仅依赖图像中的光谱特征进行分类，没有考虑到空间特征，实际的分类效果中椒盐现象严重。

针对上述问题，本文中在空谱联合特征提取阶段充分考虑高光谱图像中空间数据与光谱数据的特性，设计了一种基于3维卷积递归神经网络（3-D convolutional recursive neural network，3-D-CRNN）的高光谱图像分类方法。采用3-D-CNN与双向递归神经网络（bidirectional RNN，BiRNN）分步提取高光谱数据的空间特征与光谱特征，形成空谱联合特征，最后通过Softmax函数训练分类器实现最终的分类。该方法可以实现端到端的训练，在不破坏数据结构的前提下，充分利用空间与光谱数据所提供的语义信息，提取到的特征也更具辨别性。在Pavia University与Indian Pines高光谱数据上验证了本文中方法的有效性。

1 3维卷积递归神经网络的高光谱图像分类方法

1.1 高光谱图像中光谱与空间信息的特性

高光谱图像中含有丰富的光谱信息与空间信息，不同信息具有各自不同的特性。高光谱图像中光谱信息的光谱分辨率较高，每个像元都具有连续的光谱曲线［15］，也就是说，单个波段与相邻几个波段之间的像元亮度值（digital number，DN）具有一定的相关性。随着波段间距离的增加，这种相关性会逐渐减弱。在高光谱图像分类中，空间信息主要指空间上下文信息，其特性具体表现为空间位置上距离较近的像元属于同一类地物的概率比距离较远的可能性大［16］。分类过程中合理利用空间信息能够有效提升分类精度，削弱椒盐现象［17］。进行分类时需要同时考虑到两类信息的特性，采用合适的特征提取策略，以此提升高光谱图像的分类效果。

1.2 3-D-CNN提取空间特征

CNN最初是应用在2维结构的图像数据上，在提取图像的空间特征上表现出极佳的效果。绝大多数CNN使用的都是2维卷积核，但是高光谱图像具有上百个波段（即上百张2维图像），将2维卷积核应用到高光谱图像的处理上时将会产生大量参量，对于标注数据较少的高光谱图像来说，极易造成过拟合现象［18］。

3维卷积核可以同时在3个方向上进行卷积，输出为一个3阶张量。在3-D-CNN卷积层第i层，第j个特征图中，（x，y，z）位置的输出可通过如下公式计算：

式中，f（·）是激活函数；bij为偏置；Bi，Wi和 Hi是 3维卷积核的大小，即Bi是3维卷积核在光谱维的尺寸，Wi和 Hi分别是3维卷积核的宽和高；uijk，hwb是与（i-1）层第k个特征图相连接的卷积核。相对于2维卷积，3维卷积涉及的参量较少，更适合于样本有限的训练任务。除此之外，对比2维卷积核与3维卷积核对高光谱图像的卷积结果（如图1所示），利用2维卷积核提取特征，可能会损失高光谱图像的3维结构信息。3维卷积核能够充分地提取高光谱数据的空间特征，并且保留光谱维上的数据维度大小。因此本文中采用3-D-CNN进行空间特征的提取。

Fig.1 The comparison of two kind of convolution kernel processing results

卷积核的大小对模型训练效果和速度有重要影响。有研究表明［19］，大小为3×3的卷积核可以在参量较少的情况下，表现出更好空间特征提取效果，所以3维卷积核的大小定为3×3×1。3-D-CNN提取空间特征的策略为：从原始高光谱图像中提取大小为n×n×B（B指高光谱图像波段数）的数据块，使用3-D-CNN对数据块进行卷积处理，卷积核大小为3×3×1。经过几个卷积层的非线性变换之后将中心像元周围一定大小邻域的空间信息融入到中心像元中，生成一个大小为1×1×B大小的向量，完成空间特征的提取。

1.3 BiRNN提取光谱特征

高光谱图像的光谱数据是一种序列数据，波段之间具有序列相关性。随着波段间距离的增加，这种相关性会逐渐减弱，说明光谱数据中各个波段之间短期依赖性较强，而且对前后信息都具有依赖性。为了降低训练成本，在训练时不考虑其长期信息记忆的损失，采用参量较少的标准RNN。但是标准的RNN处理序列数据时只会将之前的信息记忆应用于当前的输出，却忽略了之后的信息。

BiRNN是RNN的一种变体，其基本思想是对同一组序列数据分别用向前和向后两个RNN进行训练，两个RNN同时与输出层相连，这种结构为每一个输出提供前后的上下文信息。因此，本文中采用BiRNN对光谱维上的特征进行提取，网络结构如图2所示。其中包含6个权重：输入层到前向和后向隐层（U1，U2），隐层到隐层（Q1，Q2），前向和后向隐层到输出层（V1，V2）。

Fig.2 Schematic diagram of BiRNN

1.4 模型结构

本文中设计的3D-CRNN模型包括空间维特征提取与光谱维特征提取两部分。空间维特征提取部分主要由3-D-CNN组成，卷积核大小皆为3×3×1，步长为1。卷积层之间不设池化层，以保留小目标的特征信息。在卷积核的数目设置上，按照CNN的普遍设计比率，后一层的卷积核数目是前一层的两倍，初始层卷积核的数目设为4。每个卷积层的输出经过批归一化（batch normalization，BN）层与ReLU激活函数。对最后一个卷积层输出进行丢弃处理，避免因密集采样而导致模型过拟合。数据集准备过程中，需要对原图像边缘进行一定的零填充，然后以原图像上的每一个像元为中心点依次选取n×n×B大小的像素块作为训练样本与验证样本，其中n×n为高光谱图像空间维上的采样大小，B指光谱波段数。为了满足光谱维特征提取部分的输入格式，处理后的数据大小必须为1×1×B。因此，对于输入到训练网络中不同大小的像素块，可以通过改变卷积层的层数实现改变输出大小的目的，例如：对于大小为5×5×B的像素块，卷积层层数设为2；对于大小为7×7×B的像素块，卷积层层数设为3，以此类推。光谱维特征提取部分由Bi-RNN构成，递归层的层数设为1，隐藏层特征数设为32。将输出经过BN层，使用Tanh函数作为Bi-RNN的激活函数，最后将BiRNN的输出结果输入到全连接（fully connected，FC）层中，使用Softmax作为训练分类器的损失函数。整个网络结构如图3所示。

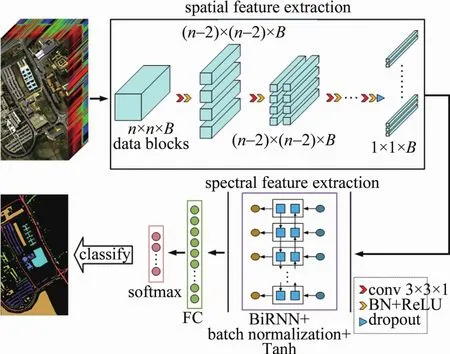
Fig.3 3-D-CRNN network structure diagram

2 数据集与实验准备

2.1 实验数据集

为了评价模型的分类效果，选择Pavia University与Indian Pines两个具有代表性的高光谱图像数据集对模型分类效果进行验证，如表1所示。这两个数据集在传感器、空间分辨率、样本数量以及地物种类等方面具有较大差异，更能综合地反映出模型的分类性能。分类评价指标采用平均分类精度、总体分类精度与衡量分类精度的kappa系数。

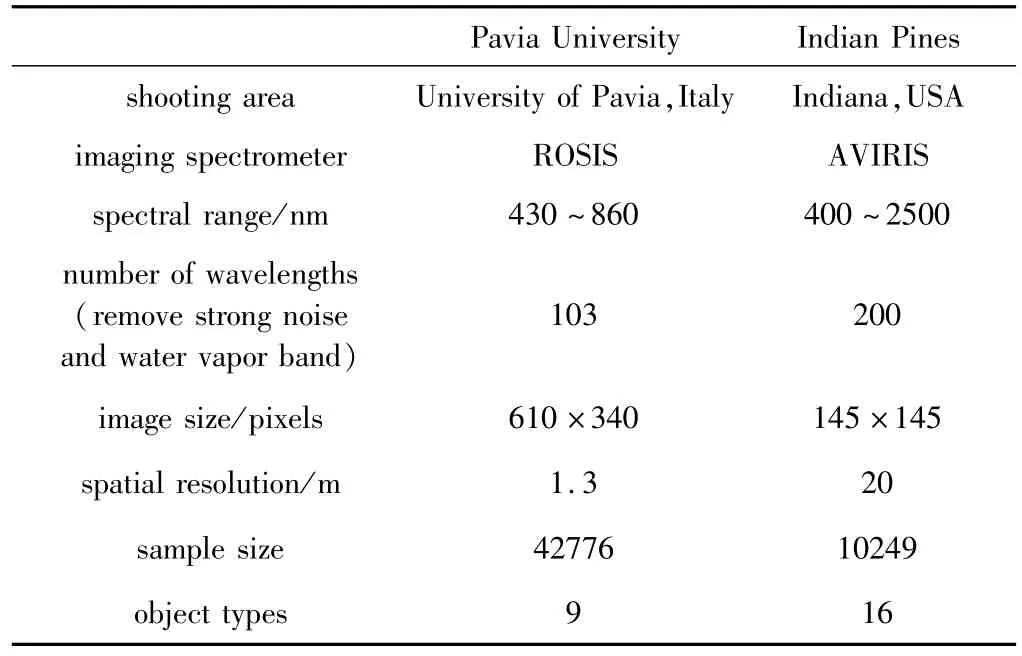
Table 1 Hyperspectral image data set

2.2 实验环境及参量设置

实验的硬件平台是一台个人计算机，配置为Intel（R）Core（TM）i7-8750H CPU＠ 2.20GHz 2.21GHz，8G运行内存，NVIDIA GeForce GTX 1060显卡。软件平台均采用Windows 10系统下的Python 3.6.0和Py-Torch 0.4.0。

使用随机梯度下降优化器进行网络训练，初始学习率为0.001，动量为0.9，学习率更新采用自适应调整策略。由于训练集较小，所以模型的单位样本数量取为16，丢弃率设为0.5，网络训练正反流程数设为150。在数据准备阶段，对数据样本进行随机水平或垂直翻转并添加噪声，降低过拟合概率，并对每类样本随机打乱，确保数据随机分布。实验数据的训练集和验证集分配比例为4∶6。

3 实验结果分析

在3-D-CRNN模型中，训练样本大小为n×n×B，B为高光谱图像波段数，空间维大小为n。若n过小，空谱特征中包含的空间信息量不足，会影响分类效果；若n过大，局部空间区域中不属于同一类别的像元数目可能会增多，对分类产生消极影响［20］。为了确定训练样本中最合适的空间维大小，分别选择大小为5×5×B，7×7×B，9×9×B，11×11×B，13×13×B，15×15×B，17×17×B的像素块作为训练样本对3-D-CRNN网络进行训练，不同大小的训练样本对应的总体分类精度和训练时间如图4所示。可以看出，在Pavia University数据上，随着像素块大小的增加，总体分类精度先上升后下降，n＝11时精度最高；训练时间也不断增长，并且增长幅度逐渐增大。在Indian Pines数据上也表现出相同的变化情况，当n＝15时，总体分类精度最高。因此无论是从分类精度方面，还是从训练时间上考虑，都应该针对不同特点的数据选择合适的输入像素块大小。同时，对比图4a和图4b可以发现，由于Pavia University数据的空间分辨率比Indian Pines数据要高，混合像元较少，所以前者的分类精度普遍高于后者。

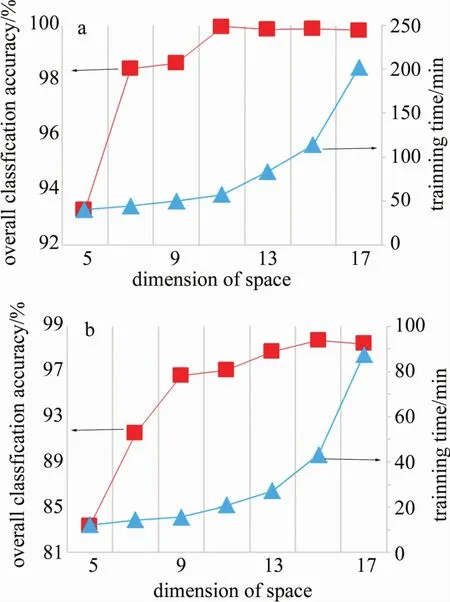
Fig.4 Overall classification accuracy and training time corresponding to different training samples in two data setsa—Pavia University data se—Indian Pines data set

将本文中提出的3-D-CRNN模型分别与近几年来高光谱图像分类文献中的 CNN方法［8，10-11］进行比较以评价模型性能。单目3维深度卷积神经网络［10］（monocular 3-D deep CNN，M3D-DCNN）与 3-DCNN［11］同时利用了高光谱图像中的空间信息与光谱信息；1-D-CNN［8］仅利用高光谱图像中的光谱信息进行分类。同时，为了进一步证明使用BiRNN提取光谱特征的优越性，本文中参考MOU等人［14］设计的RNNGRU模型（门控循环单元（gate recurrent unit，GRU））中的网络设计与参量设置，使用 BiRNN模块构建RNN-BiRNN模型对高光谱图像进行分类。并与原文献中的RNN-GRU模型进行比较。

为了更好地对比分类效果，所有模型中训练集与验证集分配比例和正反流程数均与本文中模型相同，权重初始化、学习率以及优化器的选择等条件则与原文献相同。以上模型在两个数据集上的分类精度如表2、表3所示。

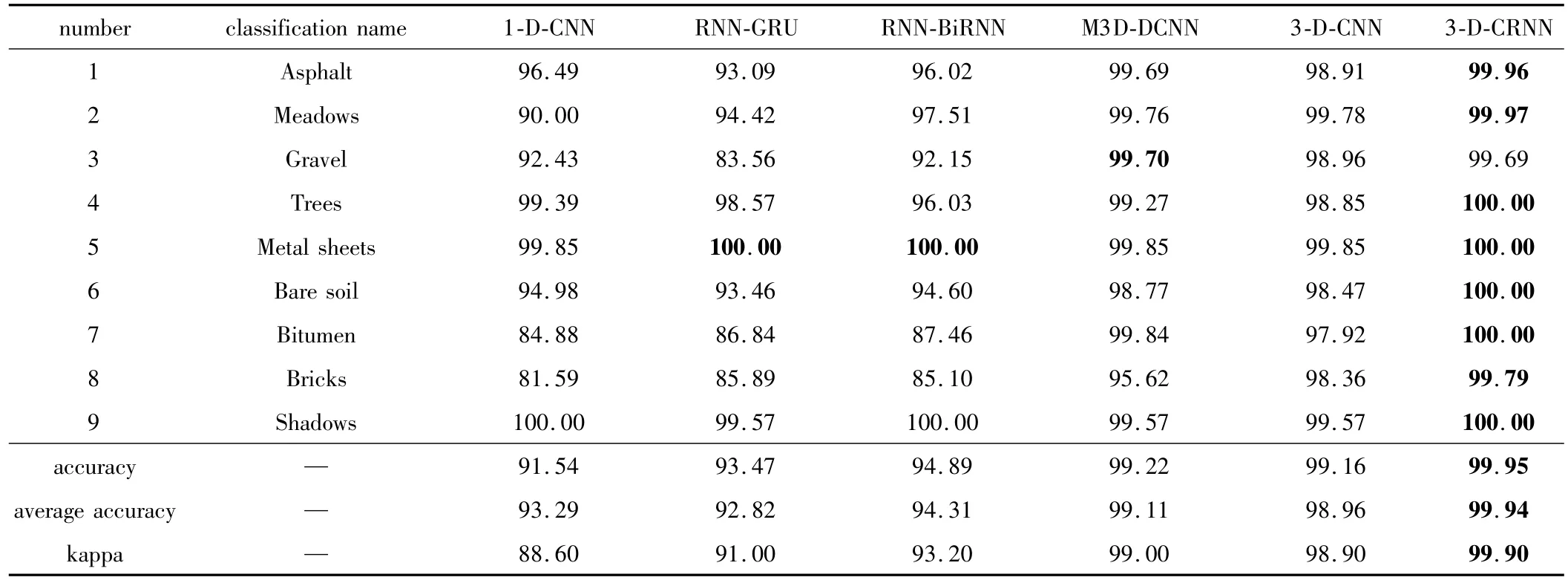
Table 2 Classification accuracy of different methods on Pavia University data／%

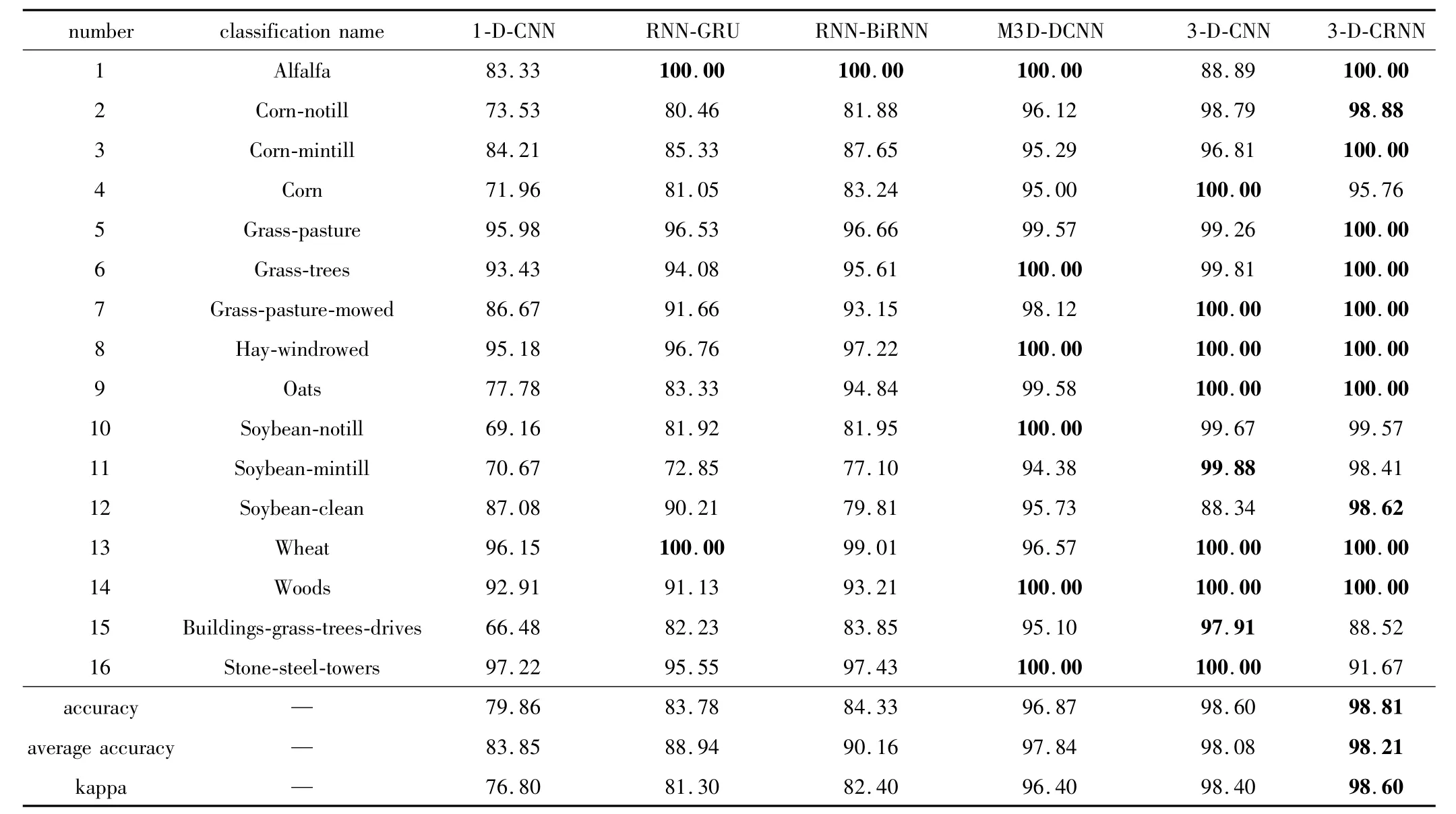
Table 3 Classification accuracy of different methods on Indian Pines data／%

对比表2、表3可知：（1）将仅利用光谱信息的方法（1-D-CNN，RNN-GRU，RNN-BiRNN）与同时考虑空间光谱信息的方法（M3D-DCNN，3-D-CNN，3-DCRNN）进行对比，可以发现同时考虑空间与光谱信息的方法能够有效提高分类精度；（2）使用同样的方法进行分类时，在Pavia University数据集上的分类精度要优于Indian Pines数据集，这也与上面得出的结论相同，即空间分辨率越高，混合像元的情况也越少，分类精度也就越高；（3）对比RNN-GRU与RNN-BiRNN两种方法，可以发现RNN-BiRNN方法在两种数据集上的分类精度与kappa系数均高于RNN-GRU，这说明RNN-BiRNN在提取光谱特征方面要优于RNN-GRU，间接上也证明了3-D-CRNN模型设计的合理性；（4）对比M3D-DCNN，3-D-CNN和3-D-CRNN 3种方法，在Pavia University和 Indian Pines数据集上，3-D-CRNN在分类精度与kappa系数高均于其它两种方法，总体分类精度分别达到了98.81%和99.95%，实际的分类效果图与真实地物分布也十分接近；但是在Indian Pines数据集上，本文中的方法对第15、第16类地物的分类精度与其它两种方法相比相差较大，说明对于3-D-CRNN难以对复杂地物组成的类别进行精确分类。

图5、图6是不同模型在两个数据集上的分类结果图。从图中可以发现，对比3-D-CNN和3-D-CRNN两种方法的分类结果图可以发现，尽管两者分类精度相差不大，但是相比于3-D-CRNN，3-D-CNN方法的实际分类效果与真实地物分布相差较大，对小目标的识别能力较弱。可见，分类精度并不一定能够代表实际的分类效果。

Fig.5 Classification result graph of different methods on Pavia University dataa—true color imag—feature label imag—1-D-CN—RNN-GR—RNN-BiRN—M3D-DCN—3-D-CNN h—3-D-CRNN

Fig.6 Classification results graphs for different methods on Indian Pines dataa—true color imag—feature label imag—1-D-CN—RNN-GR—RNN-BiRN—M3D-DCN—3-D-CNN h—3-D-CRNN

4 结 论

设计了一种基于3维卷积递归神经网络的高光谱图像分类方法。该方法针对高光谱图像中光谱信息与空间信息的特性，使用3-D-CNN与BiRNN作为基础结构，分步提取高光谱图像的空谱联合特征，能够充分提取数据中的语义信息，提取到的特征也更具辨别性。除此之外，对比分析了不同大小的训练样本对分类精度的影响，针对不同特点的高光谱图像数据选择各自最合适大小的训练样本。在Pavia University和Indian Pines两个数据上的分类实验结果表明，本文中提出的方法能够有效提升分类精度，在真实图像上也能达到较好的分类效果。

高光谱图像中包含丰富的光谱信息与空间信息，从特征提取的角度来看，如何发挥两类信息各自的优势，提高深度学习模型在提取特征方面的质量和效率是下一步研究的重点，尤其是探索RNN在这一方面的应用。另外，现有的评价高光谱图像分类效果的标准过于单一，在分类实验中，较高的分类精度并一定代表实际的分类效果一样好，如何探索出更加全面、更能代表实际分类效果的评价标准也是人们需要关注的方向。