内外圈装配过盈量对圆柱滚子轴承力学性能的影响
2020-07-08粟爽格
粟爽格, 安 琦
(华东理工大学机械与动力工程学院,上海 200237)
圆柱滚子轴承是应用最广的滚动轴承类型之一。使用圆柱滚子轴承时,内圈和轴以及外圈和轴承座孔之间采用的是紧配合安装,在接触面上会产生较大的压紧力,使轴承内圈膨胀、外圈压缩变形,势必会对轴承的力学性能产生影响,迄今对此鲜有有效的计算方法。
Palmgren[1]研究了轴承在径向、轴向和力矩载荷作用下的变形与滚动体载荷分布,建立了线弹性接触问题中载荷与变形公式,即Palmgren 公式,该公式在工程实践中得到广泛应用。Houpert[2]研究了滚子与内外滚道接触区域的变形,并结合相关参数进行曲线拟合,建立了考虑滚子直径与内外圈厚度影响的滚子与内外滚道接触变形计算公式。Chen等[3]通过离散法将接触面离散,研究了滚道有限接触长度的力学性能,计算了圆柱滚子轴承的接触应力和径向刚度。Peng 等[4]建立了考虑滚子误差影响的圆柱滚子轴承力学模型,研究了滚子误差对滚子与内外滚道的接触应力以及轴承内圈轴心轨迹的影响。甄妮等[5]建立了考虑滚珠尺寸误差时,滚珠螺旋的受力和寿命计算模型。李肖杰等[6]建立了圆柱滚子轴承和轴的过盈配合模型,研究了轴承形状误差与过盈量等因素对轴承内圈滚道径向变形的影响。蔄靖宇等[7]通过对油套管锥螺纹与接箍端面间径向过盈配合的分析,研究了初始密封面间隙、表面粗糙度和拧紧力矩对油套管螺纹端面密封性能的影响。Kim 等[8]基于系统动力学方法,建立了考虑轴承装配公差与热变形等因素情况下的主轴轴承综合预测模型。郭铁能等[9]建立了考虑了子内圈离心膨胀和热位移的轴承过盈配合模型,结合Harries 轴承动力学模型,进行了轴承配合过盈量对主轴动力学特性影响的分析。王秋志等[10]采用有限元方法分析了圆柱滚子轴承在无误差时的基础应力分布,并且探讨了轴承存在游隙、滚子直径等制造误差和内外圈相对偏转等装配误差时轴承接触应力的分布规律和最大接触应力的变化趋势。Fred等[11]研究了在轴承内圈常见干涉配合情况下,环向应力对角接触球轴承和深沟球轴承的滚动疲劳寿命的影响。王保民等[12]基于Hertz 弹性接触理论,建立了角接触球轴承的力学方程,采用Newton-Raphson 迭代法进行求解,分析了预紧力对角接触球轴承疲劳寿命的影响。
综上所述,目前虽然有人对滚动轴承装配问题开展了研究,但研究过程大量使用简化和近似方法,所建立的力学模型缺乏精确性,还有一些研究采用现有的有限元软件进行分析。因此,目前该方向的研究尚不够深入,也没有形成可以对由于装配所引起的轴承应力和变形进行精确计算的力学模型。本文以圆柱滚子轴承为研究对象,通过对其装配过程的力学分析,应用有关弹性力学理论,构建了能够在考虑轴承内外圈配合精度的条件下、对其内外圈装配面的挤压应力和变形进行计算的力学模型,进而研究轴承内外圈装配过盈量对其力学性能的影响规律。
1 力学分析及建模
1.1 不考虑装配变形时的力学性能计算方法
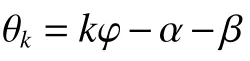
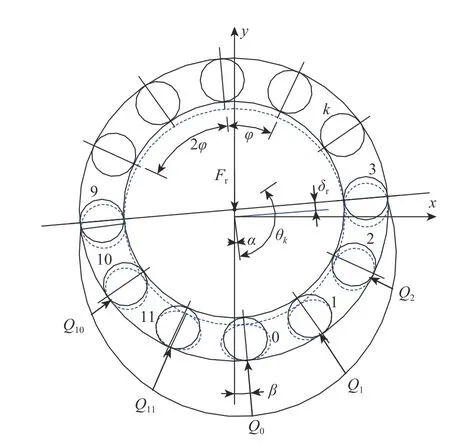
图1 轴承载荷分布Fig. 1 Bearing load distribution
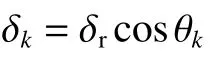

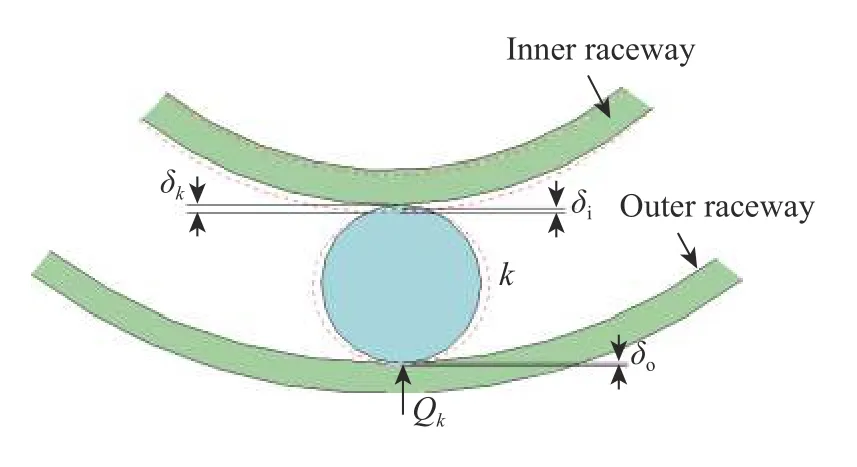
图2 滚子与内外滚道接触Fig. 2 Roller contact with the inner and outer raceways


根据上述理论即可通过编程迭代求得各滚子的受力。
1.2 考虑内外圈装配变形的力学分析及建模
1.2.1 轴承内外圈装配变形分析 滚动轴承在装配时,内圈与轴以及外圈与轴承座的配合都是紧配合,会存在一定的过盈量,导致内圈产生径向膨胀,外圈产生压缩变形。这种内外圈的变形将会影响每个滚子的实际受力。
在进行力学分析时,首先提出以下假设:
(1)滚子与内外圈的接触变形在弹性范围内;
(2)装配引起的变形仅表现为轴承内外圈直径的变化,其内外圈滚道的几何形状保持不变;
(3)装配变形后,轴承内外圈材料的力学性能不变。
轴承内圈与轴、外圈与轴承座在安装时处于过渡配合,甚至过盈配合状态,符合厚壁圆筒理论的应用条件。文献[13-14]也曾采用厚壁圆筒假设对轴承的装配问题进行过研究。本文采用厚壁圆筒理论对轴承内外圈由于装配应力产生的弹性变形进行计算。图3(a)所示的厚壁圆筒过盈套装在一个圆柱上,图3(b)所示的厚壁圆筒过盈套装在一个半无限体上。

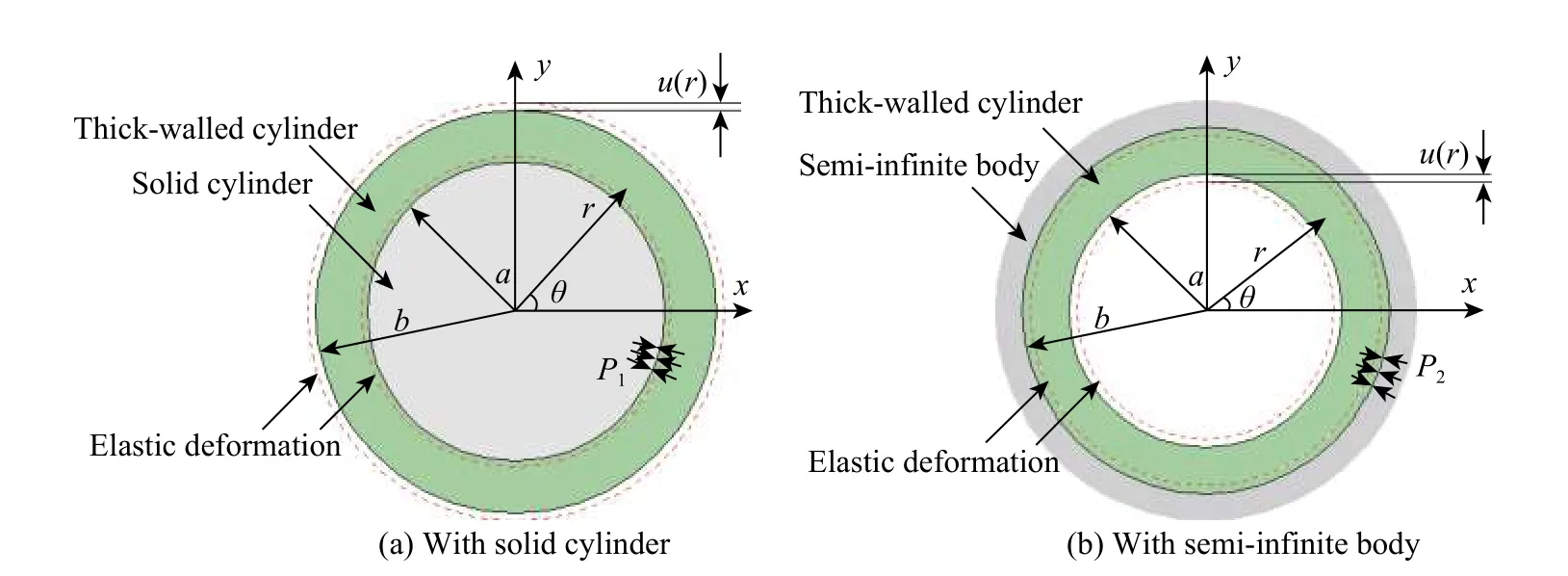
图3 厚壁圆筒示意图Fig. 3 Schematic diagrams of thick-walled cylinder
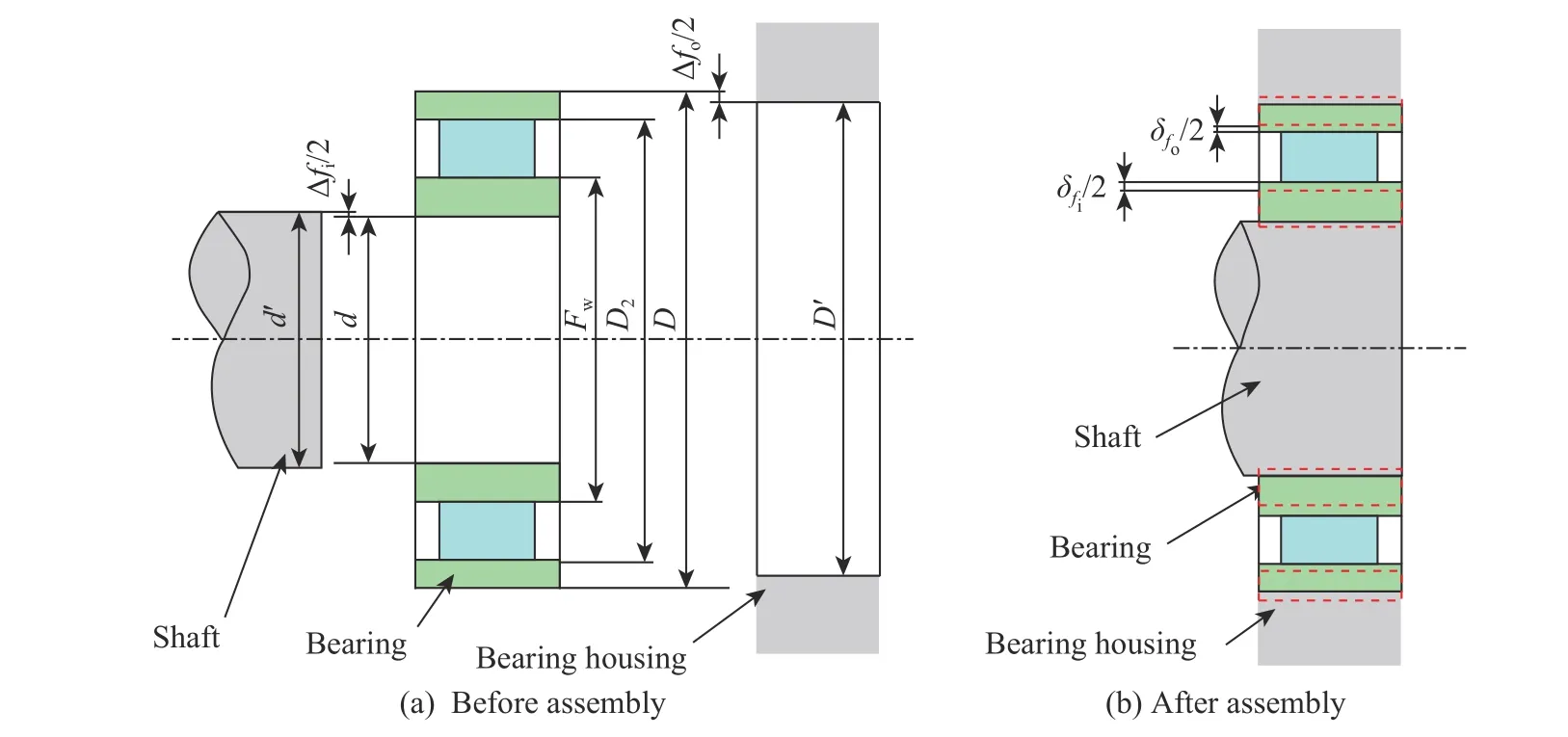
图4 轴承过盈装配示意图Fig. 4 Schematic diagrams of bearing interference assembly


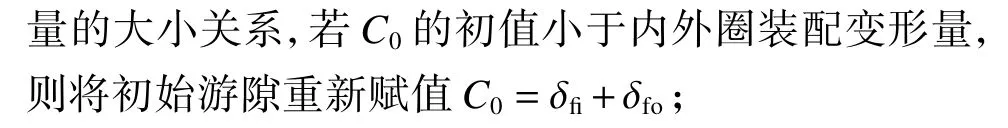

图5 轴承装配变形示意图Fig. 5 Schematic diagrams of the deformation of bearing assembly

2 算例研究

2.1 不考虑装配变形时的计算结果
图7 所示为不考虑装配影响且游隙为0 时,滚子与内外滚道接触的最大接触应力图以及圆柱滚子轴承内圈的轴心轨迹图。滚子与内外圈接触的接触应力均呈抛物线的规律变化且数值相同(图7(a));轴承内圈中心的轴心轨迹呈近似椭圆的规律变化(图7(b));内外圈相对转动一周时,轴心按照相同的近似椭圆的轨迹运动Z(滚子数)圈(图7(c))。
2.2 考虑装配变形时的计算结果

为了研究过盈量的影响,本文分别在游隙为0、9 μm 时,计算了不同的装配(过盈量)下每一个滚子的受力变化情况,结果如图10 和图11 所示。由图可以看出,随着过盈量的增大,滚子接触应力的范围增大,轴承的承载区增大。当过盈量较小时,滚子接触应力以抛物线规律变化,接触应力的峰值随过盈量的增大逐渐减小;但当过盈量增大到一定程度时,滚子将在整个圆周上都承受应力,并且最大接触应力也会产生明显的增加。
3 结 论
(1)以圆柱滚子轴承为研究对象,通过力学分析,结合厚壁圆筒理论,构建了能够在考虑轴承装配过盈量条件下对圆柱滚子轴承滚子与内外滚道接触应力和轴心轨迹进行计算的方法,实现了在考虑内外圈装配过盈量条件下,对每一个滚子的应力进行定量计算。

图6 计算流程图Fig. 6 Calculation flow chart

表1 轴和轴承座的结构和材料参数Table 1 Structure and material parameters of the shaft and bearing housing

表2 NU306E 圆柱滚子轴承的结构和材料参数Table 2 Structure and material parameters of NU306E cylindrical roller bearing
(2)采用本文所建立的算法,以圆柱滚子轴承NU306E 为算例,研究了轴承内外圈装配过盈量对滚子受力的影响规律。研究表明,不考虑装配过盈量影响时,轴心的位移近似为椭圆,滚子与内外滚道的接触应力均呈抛物线变化且每个滚子的最大接触应力值相同。当保持轴承装配过盈量不变时,随着初始游隙的增大,滚子接触应力的范围逐渐减小,接触应力的最大值逐渐增大;当初始游隙保持不变时,随着过盈量的增大,滚子接触应力的范围逐渐增大,滚子接触应力的最大值逐渐减小,过盈量增大到一定程度时,滚子在整个圆周上都受力,且滚子接触应力的最大值显著增大。
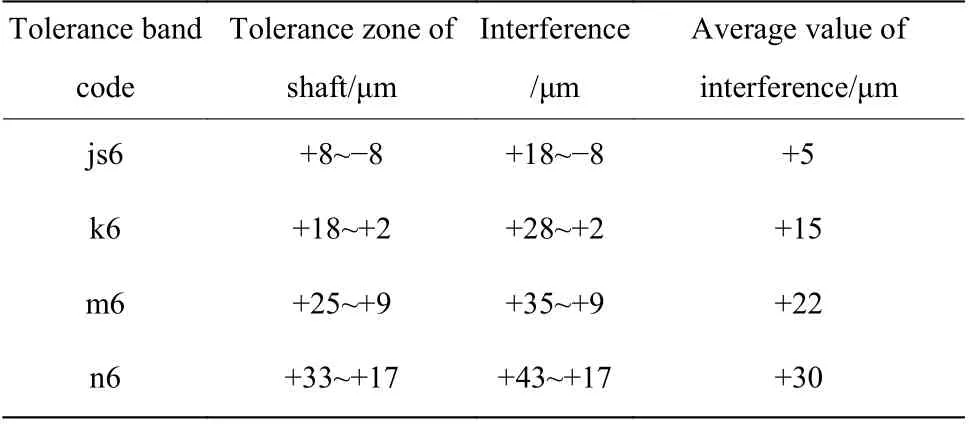
表3 轴承与轴的配合参数Table 3 Matching parameters of the bearing and the shaft

表4 轴承与轴承座的配合参数Table 4 Matching parameters of the bearing and the bearing housing
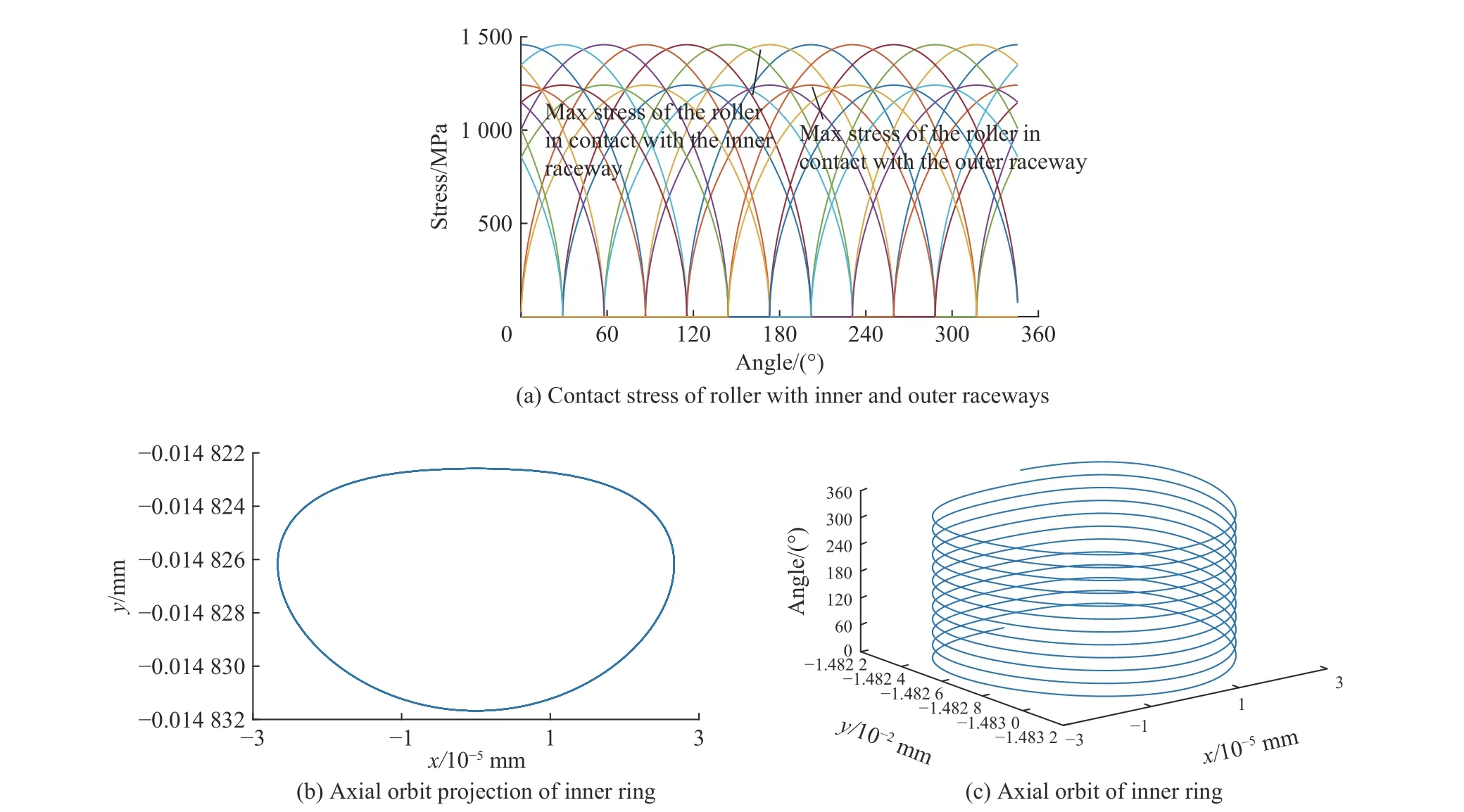
图7 不考虑装配和游隙时滚子的接触应力与轴心轨迹Fig. 7 Contact stress of roller and axial orbit without assembly and clearance
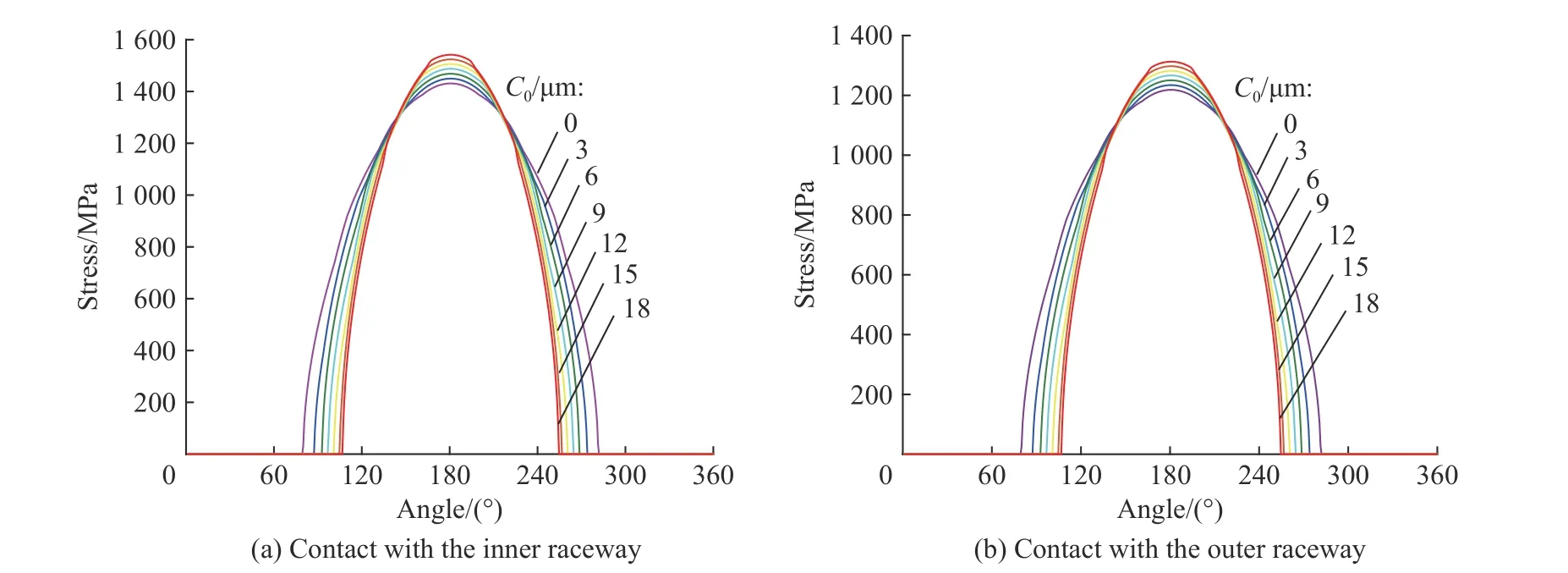
图8 装配公差为js6/K7 时游隙对接触应力的影响Fig. 8 Influences of clearance on contact stress when assembly tolerance is js6/K7

图9 装配公差为m6/JS7 时游隙对接触应力的影响Fig. 9 Influences of clearance on contact stress when assembly tolerance is m6/JS7
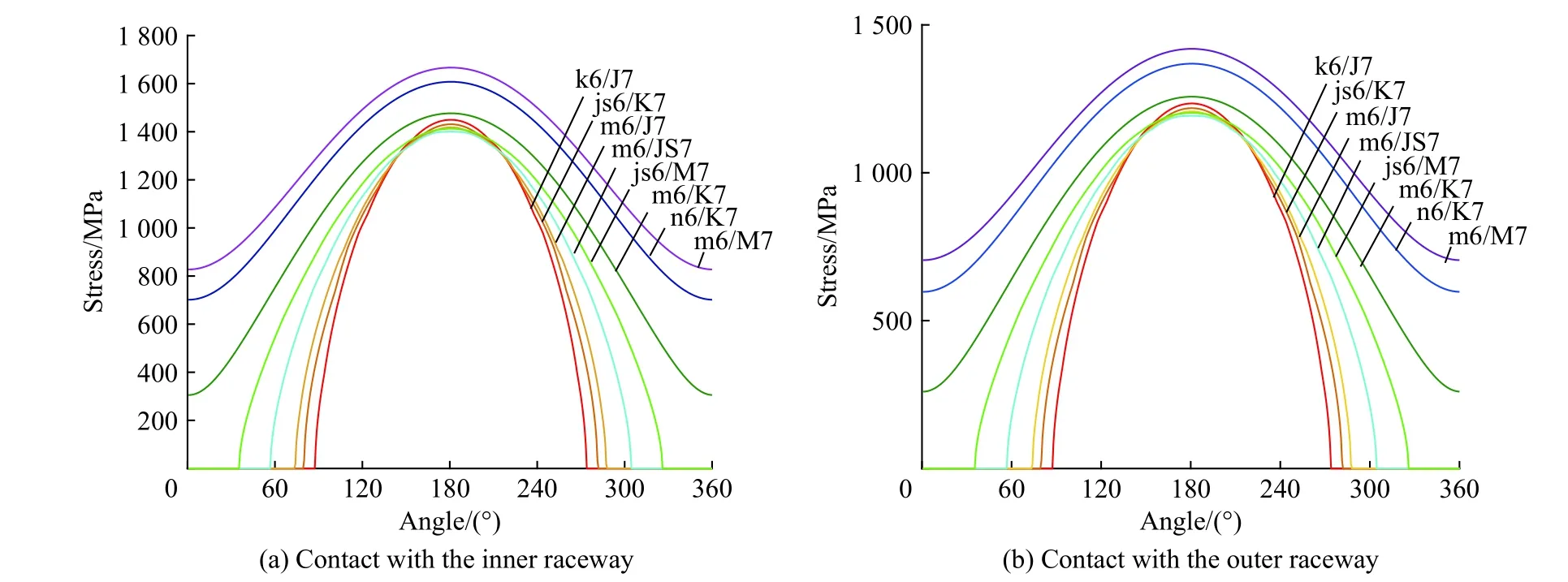
图10 游隙为0 μm 时过盈量对接触应力的影响Fig. 10 Influences of interference on contact stress when clearance is 0 μm
图11 游隙为9 μm 时过盈量对接触应力的影响Fig. 11 Influences of interference on contact stress when clearance is 9 μm
