循环流化床锅炉循环流率在线测量方法研究

刘贤东，吴玉新，张 扬，周 帅，杨海瑞，张 海，吕俊复，张 凯

(1. 清华大学 能源与动力工程系 热科学与动力工程教育部重点实验室，北京 100084；2.太原锅炉集团有限公司，山西 太原 030023)

0 引 言

循环流化床(circulating fluidized bed，CFB)锅炉燃烧技术一种高效低污染的燃煤技术，近些年来发展迅猛[1-4]。目前我国在建以及投运的CFB锅炉累计4 000余台，总装机容量也超过1亿kW[5]。循环流率(Gs，kg/(m2·s))是循环流化床设计与运行的重要参数，定义为CFB炉膛中单位截面内循环灰的质量通量。不同Gs值对应于不同流动状态，只有当炉膛内Gs超过饱和携带率时，炉膛内才能达到快速流态化状态[6]，进而获得较好的燃烧状态和传热能力[7]。新近研究[8]表明，如果炉膛内流态设计合理，CFB锅炉可在不使用选择性催化还原、选择性非催化还原等烟气脱硝技术条件下，达到原始NOx排放低于50 mg/Nm3的超低排放水平。循环流率Gs是流态的表征变量，Gs的实时在线监控对CFB锅炉流态优化与调整，乃至CFB锅炉整体性能提升具有重要意义。

虽然Gs备受关注，但目前尚无成熟的可应用于实际锅炉中的Gs在线监测技术[9]。部分学者在实验室开发了一些测量CFB的Gs值方法，但大多受限于锅炉内高温环境和强烈的颗粒磨损而不能直接应用于真实CFB锅炉的在线实时测量。Burkell等[10]总结了CFB循环流率测量中常用的5种方法：孔板流量计、量热法、蝶阀法、下降时间法和冲击式流量计法。对于孔板流量计而言，低流率时示数太小难以检测，高流率时波动太大，且对流动的干扰破坏比较严重。蝶阀法常用于冷态试验，但高温时该方法会破坏锅炉正常循环且难以对物料堆积速率进行观测[11]。量热法测量精度受限于传热系数估计的准确性，会为锅炉带来额外热损失[12]。下降时间法是通过测量示踪颗粒的下降速度来估算床料速度，但高温下难以对示踪颗粒进行测量[13]。冲击式流量计法是将冲击片放入立管中，并通过悬臂梁的结构将颗粒冲击信号转化为受力信号后进行测量。该方法已在冷态试验台上得到应用[14]，该方法的机械测量特性使其有望推广到高温测量。

此外，一些学者提出其他方法。Davies等[15]对声学方法测量固体循环流率进行总结，但这些方法均无法耐受高温环境。Medrano等[16]采用颗粒提取、粒子图像测速(particle image velocimetry，PIV)及数字图像分析(digital image analysis，DIA)、压降法3种方法测量循环流率，但颗粒取样法会破坏锅炉正常运行、PIV/DIA方法需要透明壁面用于观测。压降法是将提升管中稀相区压降与循环流率关联，但该关联公式参数与锅炉设计有关，只能对同一台锅炉进行定性估计，不具有可推广性。

总之，目前尚未有能够成熟应用于工业CFB锅炉中的循环流率测量方法。理想测量方法应具有能在线测量、对流场影响小、能耐受高温等特点，而通过对现有方法的比较与分析，冲击式流量计法有潜力满足以上需求。本文基于冲击法的原理，提出了一种CFB锅炉Gs在线测量方法，并开发出了原理样机在实际CFB锅炉上进行工业试验，验证了其可行性。本文的研究成果是该方法的初步探索，为Gs测量技术的进一步开发提供了理论指导。

1 CFB锅炉循环流率Gs的冲击式测量原理

流体绕流掠过物体时，会对物体产生一定的作用力，作用力大小与流体掠过物体的速度有关。冲击式流量计就是利用这种原理实现对循环流率的测量。冲击式流量计测量示意如图1(a)所示。该流量计的原理性核心部件有靶片、靶杆和固定端3部分。靶片即为放入流场中的物体，可为圆盘、圆柱、圆球状；固定端与外壁面相连且保持稳定，不随流速变化而发生位移；靶杆是一根金属细长杆，将靶片和固定端相连，在靶杆靠近固定端的一侧安装应变传感器，用来测量靶杆当地的应变。测量时，此装置应安装在分离器下方立管密相区中靠上的位置。靶杆穿过壁面和保温层，将靶片放置在立管下方密相区中(图1(b))。锅炉运行时，立管密相区内气固两相流可视为拟流体[17]，处在单向黏性流动状态[18]。此密相区靠下的部分受到返料阀结构和返料风的影响，横截面速度分布较为复杂。而此密相区靠上的部分处在近似最小流态化状态[19]。除去壁面附近边界层内固体颗粒流速较慢外，其余部分流速分布均匀，且流速较小(量级O(0.1)，m/s)，若获得了该截面上某个点的流速，则可视为平均速度并以此计算得到立管整个横截面的质量流速，进而推出CFB锅炉炉膛内的Gs值。基于上述分析，本文提出Gs测量方法。

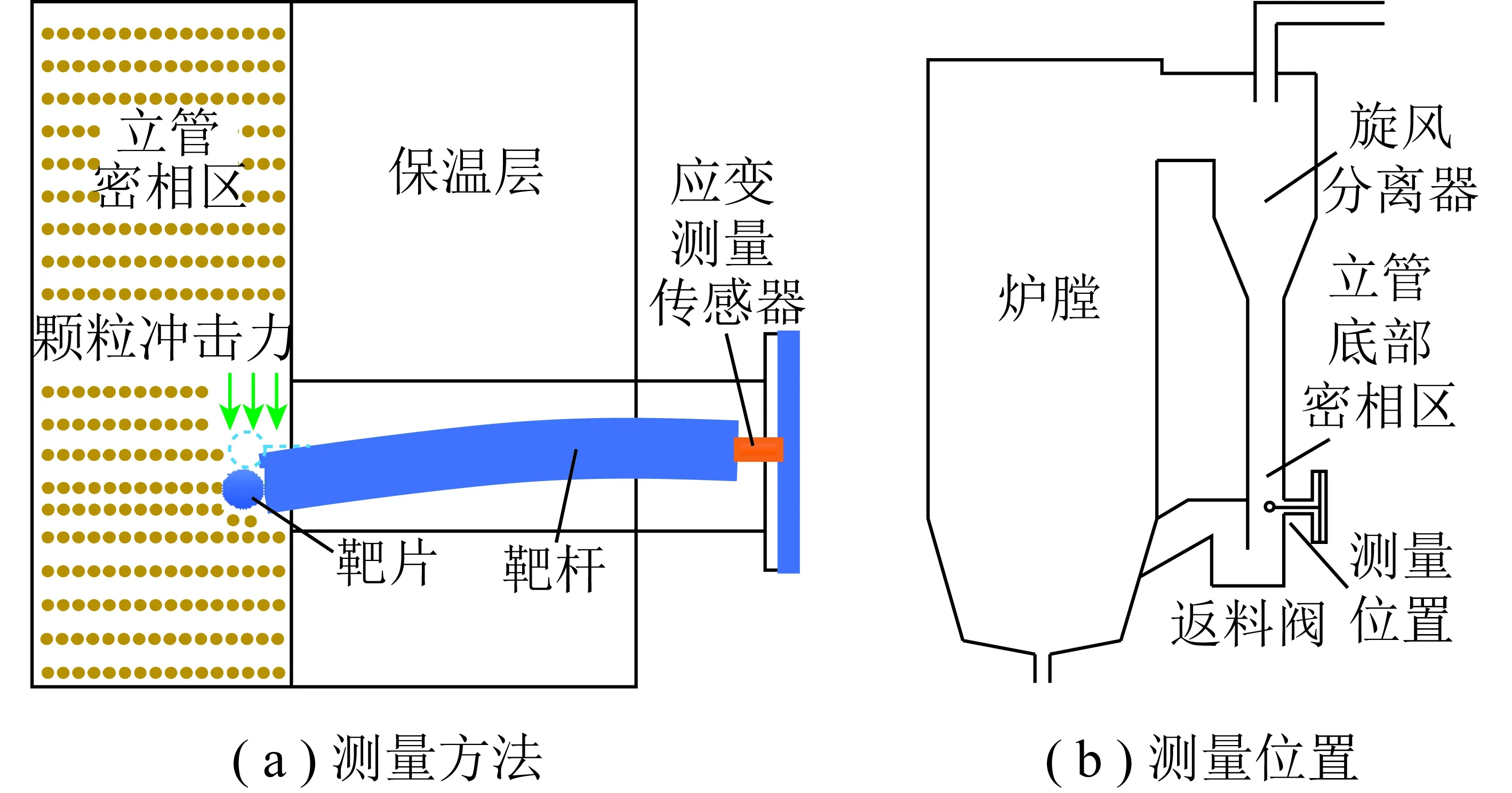
图1 冲击式流量计测量原理Fig.1 Measurement principle of impact flowmeter

立管密相区内颗粒向下流动并冲击靶片，该冲击力可根据流体理论与冲击速度、冲击投影面积相关联(式(1))[20]。

(1)

其中，F为颗粒对靶片冲击力，N；CD为气固绕流阻力系数；ρs为立管底部密相气固两相流表观密度(固体颗粒主导)，kg/m3；v为冲击速度，m/s；At为靶片在受力方向的投影面积，m2，由靶片结构及布置方向决定。立管中的固体颗粒质量流率可表示为

f=ρsv

(2)

式中，f为立管内物料颗粒向下运动的质量通量，kg/(m2·s)。

该冲击式流量计整体呈悬臂梁结构，故施加在靶片上的颗粒冲击力F与靶片本身重力(mg)的合力会造成靶杆弯曲，产生形变，被安装在靶杆根部的应变传感器感知，进而根据应变大小、靶杆几何结构和材料性质计算出冲击力大小(式(3))[21]。

(F+mg)L=Wzσ=WzEε

(3)

其中，L为靶片至靶杆根部应变传感器间距，m；Wz为靶杆根部截面抗弯截面系数，m3，由靶杆几何结构决定；σ为靶杆在应变传感器布置位置处所受应力，Pa；E为靶杆材料的弹性模量，Pa；ε为传感器所测应变值。基于式(3)，可根据传感器所测应变值得到颗粒冲击力F大小，即为式(1)中气固绕流阻力。

锅炉处在稳态运行时，锅炉内的物料近似符合连续性方程(式(4))为

GsAr=fAs

(4)

式中，Ar、As分别为炉膛(提升管)和立管的横截面面积，m2。

联立式(1)～(4)可以得到Gs值。确定气固绕流阻力系数CD是准确获得Gs值的关键。本文通过实验室直接测量的方法确定CD值和靶片的受力情况，进而使用CD值开展该方法在实际CFB锅炉上的应用研究。

2 试验研究方法装置

本文试验研究分2个层次：一是在开展实验室规模的研究工作，确定气固流动的绕流阻力系数CD；二是开展工程试验应用，确定该方法的可行性。

2.1 气固流动绕流阻力研究

阻力系数CD与气固绕流雷诺数、靶片形态有关，其影响因素较为复杂，故本文通过试验进行标定。根据式(1)测量原理，密度ρs表征气固两相流表观密度，考虑到立管密相区内气固流态为最小流化状态[19]，该密度值可对循环灰取样后测量得到。

阻力系数测量试验装置如图2所示。考虑到直接采用气固两相流冲击靶片较难实现，因此试验中转换研究对象，将固体颗粒流化至最小流化状态，控制冲击式流量计以不同速度冲击“静止”颗粒并测得其受力F(图2(a))。由式(1)计算得到不同冲击速度下的气固绕流阻力系数。试验所用物料为石英砂，密度约为2 600 kg/m3。对物料进行窄筛分(图2(b))，其平均粒径为187.23 μm。实际锅炉运行过程中循环灰密度约为2 800 kg/m3，粒径为80～200 μm，冷态试验与实际锅炉中物料具有一致性，与实际锅炉中循环灰粒径相近。装置中料层厚度为300 mm，试验过程中将靶片完全没入料层中，并控制靶片以不同速度冲击流化后的颗粒。根据以往运行经验，立管内气固流动速度在0.1～0.2 m/s，试验中将覆盖该速度范围。实际锅炉运行时靶杆为水平放置且靶片受竖直冲击力，而本试验中靶杆为竖直放置且靶片并受水平冲击力，因此需要考虑二者不同对试验结果的影响。靶杆水平放置时，计算靶片受力时需要额外考虑靶片重力和气固两相流浮力带来的影响，但靶片重力在实际计算中将予以修正(式(3))，而气固两相流浮力Fb可根据式(5)计算。

Fb=ρsVg

(5)

式中，V为靶片体积，m3；g为重力加速度，kg/m3。

计算得到浮力Fb仅为颗粒冲击力F的2%左右，实际计算中可忽略。因此，修正重力后的实验室测量结果可以应用于实际工业过程中的测量。

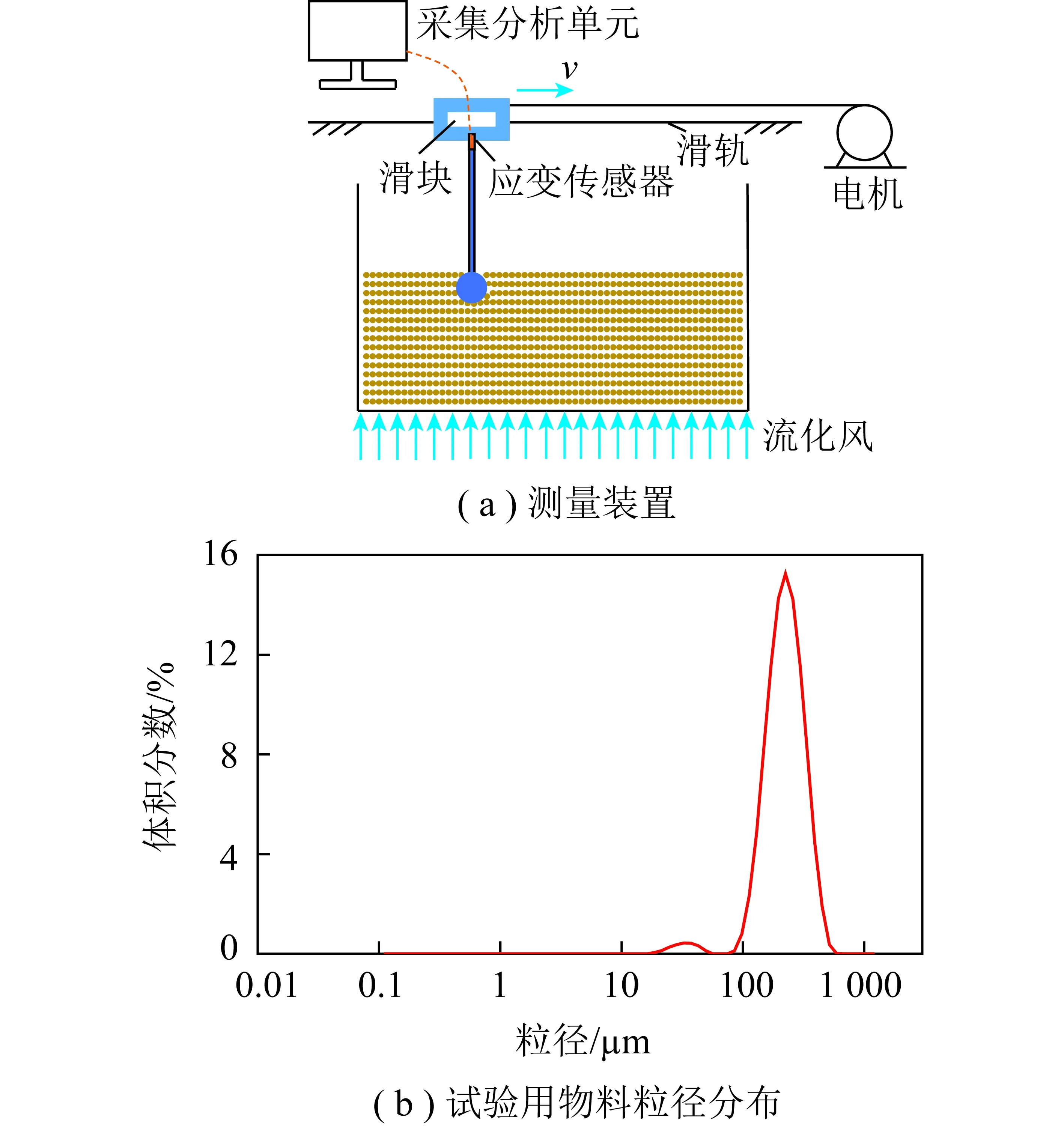
图2 气固两相流绕流阻力测量系统Fig.2 Gas-solid flow resistance measurement system

2.2 Gs在线测试方法在实际CFB锅炉中的试验研究

在线Gs测试系统如图3所示。整个系统分为冲击式Gs传感系统、送风系统和电控系统(图3(a))。冲击式Gs传感系统能够将靶片位置的f值转化为电压信号；送风系统为测量装置提供仪表风；控制电控系统能够进行信号处理，输出Gs数据，同时对数据采集过程、送风阀门等进行控制。

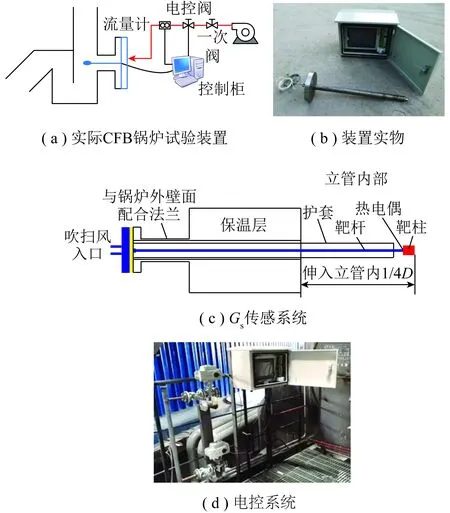
图3 Gs在线测试系统Fig.3 Gs in-situ measurement system

Gs传感系统设备安装位置选择立管底部密相区上部。实际使用过程中，考虑到颗粒冲击力的测量通过靶杆弯曲实现，因此需要为靶杆安装护套，护套为圆筒形，正好包裹住靶杆。护套仅使柱状靶片暴露于颗粒冲击下，提高测量精度。同时向护套内空隙处以流量0.5～1.0 Nm3/h送入仪表风，风量选取的原则是既能够对靶杆进行有效冷却，又防止高温物料沿靶杆反窜以保证靶杆的弯曲空间，同时防止气流量过大对靶片附近的气固流动特征产生影响。仪表风从锅炉压缩空气母管引出，通过电控阀门调节流量后送入循环流率测量装置内。在测量位置处提前在保温层内开孔，并在外壁面焊好配合法兰。靶片伸入立管内1/4D深度(D为立管直径)，以避开流动边界层。此外，在靶柱内侧安装热电偶测量靶柱处温度。

为实现高温下测量需求，该样机全部采用2520钢加工制作。应变传感器采用BHB120-4AA250型中温应变片，耐温250 ℃。该装置长度为600 mm，其中伸入立管内150 mm。利用前文所测阻力系数预估颗粒冲击力，以此作为靶片尺寸设计依据。其几何结构采用圆柱形式，尺寸为φ25 mm×30 mm。该靶片尺寸下，靶片投影面积与立管横截面投影面积之比为0.28%，故可认为该装置的放置不会对立管内气固流场造成影响。由于密相区内会随机产生一些气泡对传感器读数产生干扰，控制系统采取了滤波处理，去掉测量曲线上的毛刺。

测量方法的优势在于将感受器和传感器分开：靶片作为感受器布置于立管内，接收颗粒冲击信号，该信号通过机械方式传递给位于靶杆根部的应变传感器。该测量形式使相对脆弱的传感器远离立管高温区，且信号的机械传递方式也易于在高温下实现。该方法能够解决实际炉内高温、磨损等问题，也能实现实际锅炉的在线测量。

3 结果与讨论

3.1 气固绕流流动阻力测量

气固两相流绕流阻力F和阻力系数CD测量试验结果如图4所示。试验所测冲击速度为0.12～0.22 m/s，基本涵盖了立管内物料流速波动范围。试验中气固流态接近最小流化状态。随着速度v的增加，靶球的受力F也单调增加。根据式(1)计算得到的阻力系数CD在测试范围内随着v的增加而减小。文献[22]研究表明CD与雷诺数和表观黏度有关，而气固两相“拟流体”存在显著的“剪切变稀”现象，即表观黏度随剪切率的增加而减小。这与图4的测量现象一致。试验表明该气固两相流中绕流阻力系数较大，为后续装置设计提供了数据参考。

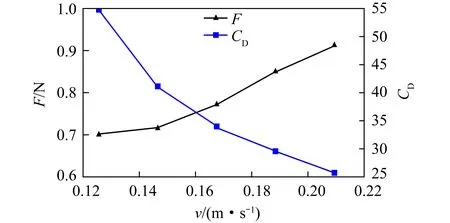
图4 气固两相流绕流阻力系数测量结果Fig.4 Measurement results of resistance coefficient of gas-solid flow

3.2 实际锅炉中Gs在线测量

样机在某116 MWth循环流化床锅炉进行试验，考虑到立管密相区处于正压，因此本装置安装在起炉前进行，锅炉运行后保持装置密封。本文选取了该锅炉起炉后60 h内数据开展分析，该段时间内锅炉运行参数与装置测量应变值如图5所示。初始时炉膛截面风速vr和炉膛稀相区压差Δp不为0，这是由于压火期间一次风全关，而二次风关小。但二次风布置位置较高，起不到流化作用，因而此时实际循环流率为0。在起炉阶段，一次风迅速全开，因而炉膛截面风速上升，锅炉负荷随之上升。由于系统惯性较大，稀相区压差缓慢上升。在停炉阶段应变测量信号不变，这是由于装置所测信号为靶杆弯曲应变，停炉时靶杆会随机停留在某一弯曲状态，因此此时虽然测量信号值不为0，但系统识别一段时间内信号值无变化，即判定此时处于停炉状态，循环流率为0。而起炉时存在一个明显的脉冲信号，且该脉冲信号缓慢减小至稳定后继续增长。这是由于刚起炉阶段立管内堆积物料从静止开始运动，转变初始时有较大的冲击力，导致了明显的脉冲信号。由于停炉时物料堆积于立管内，因而在刚起炉时立管物料流率f较大，且物料流出值大于炉膛物料返回值。

随着立管内堆积物料逐渐流入炉膛，装置所测立管物料流率逐渐减小，这与图6规律一致。而随着炉膛内风速增加且开始投煤，炉膛返回立管的物料量增加，导致立管内物料流率又开始上升。同时，炉膛内截面风速较短时间内即达到设定值并基本稳定，但装置测量信号值上升速度较慢。这是因为：一方面，截面风速达到设定值后，通过持续投煤炉膛内Gs才能开始上升；另一方面，由于系统惯性，炉膛内Gs与立管内物料流率f缓慢达到平衡。锅炉运行一段时间后，降低二次风风量并降低负荷，此时Gs下降，但由于系统状态改变不大，因而系统延迟较小，立管响应较快，而装置测量信号也捕捉到此时物料流率的瞬时变化。

图5 60 h内锅炉运行参数与应变信号值的变化Fig.5 Change of boiler operating parameter and measured strain signal in 60 hours

图6 起炉阶段测量信号的变化Fig.6 Change of strain signal in the boiler start-up process

根据前文所述测量原理可计算出该段时间内循环流率Gs实时变化值，如图7所示，该Gs值在量级上与锅炉定态设计相符[23]。目前尚未有成熟的工业循环流率测量方法，实际锅炉中常用炉膛截面风速vr与稀相区压差Δp对循环流率进行估算。炉膛截面风速vr与固体颗粒终端速度正相关，而炉膛上部稀相区压差可认为近似等于气固两相流重力压降。

Δp=ρrgΔh

(6)

其中，Δp为炉膛上部稀相区压差，Pa；ρr为炉膛气固两相流密度，kg/m3；Δh为炉膛中部压力测量点至炉膛顶部高度，m。考虑到炉膛出口压力近似为大气压，因此认为炉膛中部压力测量点所测差压即为炉膛上部稀相区压差。

由式(6)可知，炉膛稀相区压差Δp与炉膛内气固两相流密度正相关，因此可以用Δp·vr估算炉膛Gs值。

图7 Gs随时间变化Fig.7 Change of Gs with time

考虑到刚起炉阶段立管与炉膛内尚未达到流动平衡，因此选取流动稳定后24 h内运行数据(包含降负荷过程)并研究该时间段内Δp·vr与相对测量应变值间对应关系，如图8所示。Δp·vr与所测应变信号有较好的单调对应关系，进一步证明了本测量方法的可行性。

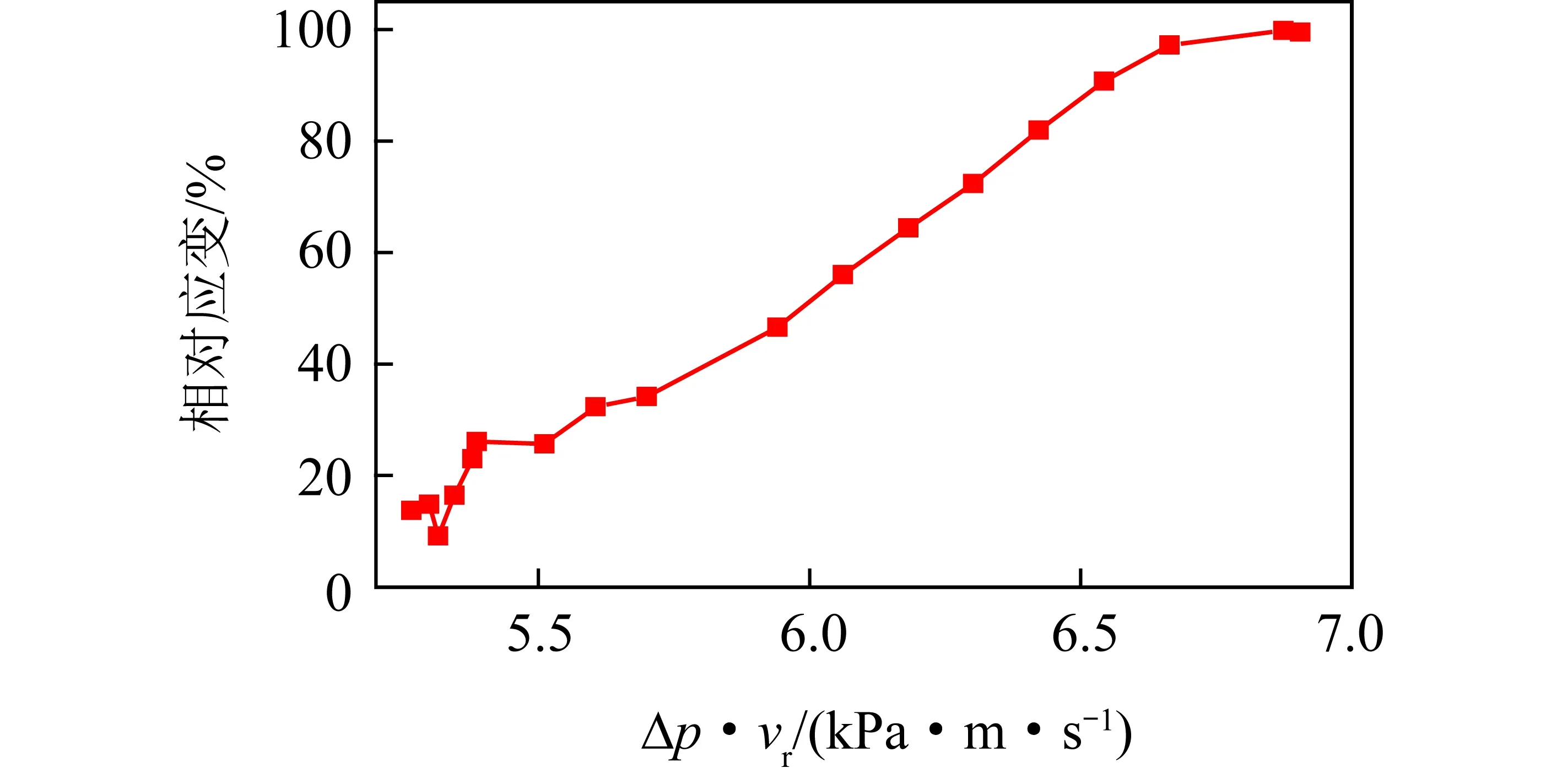
图8 Δp·vr与测量过程内相对应变对应关系Fig.8 Relationship between Δp·vr and relative strain

由前文分析可知，该新型冲击式循环流率测量方法能较好地捕捉锅炉起停炉、降负荷等过程中的循环流率变化趋势。对测量结果进行量级分析且利用Δp·vr估算并校核Gs的测量结果，证明了该测量方法的可行性。但目前仍缺乏精确测量循环流率方法，因此本装置测量数据暂时无法精确标定。后续工作中将进一步分析冲击式流量计测量过程中测量应变信号与循环流率的转换关系，进一步提高该测量方法的精度。

4 结 论

1)本文提出了一种循环流率的冲击式在线测量方法，该方法可在实际循环流化床锅炉高温环境中运行，能实现在线实时测量且不会对锅炉运行造成干扰。建立了该冲击式流量计的理论模型，利用冷态试验完善模型并在热态锅炉中进行测试。通过实验室冷态试验测量得到了不同冲击速度下的气固两相流绕流阻力F和阻力系数CD，为后续装置设计提供了数据参考。

2)基于该方法开发了Gs在线测量装置样机并在某116 MWth循环流化床锅炉中进行了热态测试，结果表明该方法能够快速及时地捕捉到起炉、停炉、变负荷等过程中Gs变化情况。

3)在热态测试中，根据量级分析，利用Δp·vr估算Gs并标定装置，证明了本测量装置的测量准确性。目前仍缺乏精确的循环流率测量方法，因此暂无法对测量信号进行精准标定。在后续工作将进一步分析装置测量中物理过程并开发标定方法。