斜拉索-磁流变阻尼器非脆弱减振控制器研究

2020-07-07冯志敏时云飞刘小锋段玉贺

农业机械学报 2020年5期

冯志敏时云飞张刚刘小锋段玉贺

(1.宁波大学海运学院，宁波315211;2.南京莱斯电子设备有限公司，南京210014)

0 引言

由车辆行驶、风雨等未知外力引起的有害振动已成为影响斜拉索桥梁安全性的重要因素。作为桥梁的主要受力构件，斜拉索极易在未知载荷作用下产生振动。减小和抑制斜拉索振动对于提高桥梁结构稳定性和安全性具有重要的工程意义［1］。

磁流变阻尼器是一种新型的智能阻尼器［2］，具有响应时间快、阻尼力可调范围大等特点，广泛应用于农用车辆、航空航天等减振控制中。斜拉索减振控制研究也逐渐集中到磁流变阻尼器半主动控制上。OU 等［3］将LQR 控制算法用于斜拉索-磁流变阻尼器控制中，提出一种半主动控制算法，并仿真验证该方法的有效性;禹见达等［4］利用位移反馈对Bang-Bang 控制算法进行改进，证明该算法对斜拉索减振有良好效果;樊晓平等［5］基于奇摄动理论，设计了抑制斜拉索振动的半主动自适应控制方法，并利用数值案例验证此算法的合理性;HEO 等［6］将鲁棒控制中的Lyapunov 法和截断最优相结合，对斜拉索振动进行控制，具有较高的可靠性。

鲁棒控制主要以被控对象和外界未知扰动不确定性为研究目标，结合相应性能指标，以获得闭环系统稳定的控制器。而非脆弱鲁棒控制不仅要考虑被控对象和未知扰动的不确定性，同时还要考虑控制器在工程调试过程中其增益参数发生的摄动状况。实际上，斜拉索减振控制器的增益参数不可能准确实现，并且在外界干扰下也可能发生改变。因此，极易降低控制器闭环系统的动态稳定性能，表现为控制器的脆弱性［7］。在传统减振控制器研究中，YEGANEHFALLAH 等［8］考虑到斜拉索系统动态参数的不确定性，提出一种解决此问题的鲁棒控制器设计方法;段玉贺等［9］为了降低振幅和振速，分别在斜拉索-磁流变阻尼器减振控制算法中引入区域极点和协方差性能指标约束的鲁棒控制理论，设计出减振效果良好的控制器。但上述研究未考虑斜拉索-磁流变阻尼器的外部扰动和减振控制器参数增益不确定性，目前将鲁棒控制中多性能指标约束［10］和非脆弱控制［11］相结合的减振控制研究成果尚不多见。

为减少斜拉索减振控制器参数摄动和外部扰动对系统性能的影响，本文提出一种多性能指标约束的非脆弱减振控制器设计方法。运用非脆弱控制和鲁棒控制中的多性能约束方法，以抑制振荡幅值和时间为目标，给出该减振控制器设计形式及求解方法，并与常规减振控制器、H∞减振控制器的减振效果进行分析对比。

1 系统模型及求解分析

1.1 系统模型建立

斜拉索-磁流变阻尼器动力学模型如图1 所示。

图1 斜拉索-磁流变阻尼器动力学模型示意图Fig.1 Schematic of dynamic model of stay cable-magnetorheological damper

斜拉索在风雨振主发生面存在极小垂度(考虑材质、安装等因素)。假设静平衡状态下斜拉索长度为L，与水平面夹角为θ，振动时斜拉索曲线为y(x，t)，静平衡下索曲线为y0(x)、索力变化量为ΔS;外部激励载荷f(t)垂直作用于斜拉索，且在二维X、Y 面内存在fx、fy;两侧磁流变阻尼器对称安装在距锚固端xd处，轴向阻尼力为fd(t)，与水平面夹角为α 且与斜拉索索长方向垂直。

结合Hamilton 原理可得斜拉索-磁流变阻尼器系统动力学方程［12］为

其中

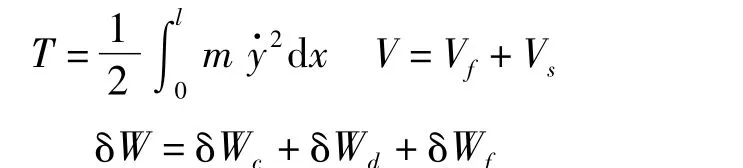
式中 T——系统动能

Vf——弯曲应变能

Vs——拉伸应变能

δWc——系统阻尼做功

δWd——阻尼器做功

δWf——外力做功

m——斜拉索单位长度质量

V——弯曲与拉伸应变能总和

δW——系统阻尼、阻尼器及外力做功总和

由于斜拉索抗弯刚度和斜拉索振动时的索力增量较小，可忽略不计，即EI≈0，E 为斜拉索弹性模量，I 为惯性矩，ΔS≈0 得n 组方程［13］为

式中 c0——斜拉索单位长度阻尼系数

S0——初始索力

qi——广义位移坐标

φi——i 阶振型函数

φid——阻尼力作用下的i 阶振型函数

φj——j 阶振型函数

令u(t)= -fd(t)，得其矩阵形式为

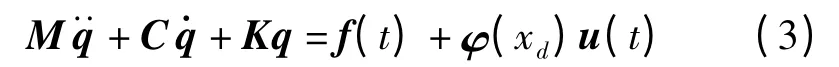
式中 M——质量矩阵 K——刚度矩阵

C——阻尼矩阵

φ(xd)——振型函数向量在坐标xd处的向量

u(t)——斜拉索所受阻尼力

1.2 求解及系统分析

1.2.1 切比雪夫级数的方程求解

M、K、C 中矩阵元素mij、kij、cij的计算十分复杂，为简化求解过程，采用切比雪夫级数计算方法，并以正弦函数表示该振型函数。斜拉索-磁流变阻尼器的振型函数可表示为［9］

其中

式中 fi——i 次切比雪夫级数系数

Ti(x)——i 次切比雪夫多项式

斜拉索采用磁流变阻尼器控制，其振动形态发生很大变化，也增加了求解过程复杂性。为提高振动时收敛速度，可用“0”阶振型表示磁流变阻尼器作用下静力变形，即

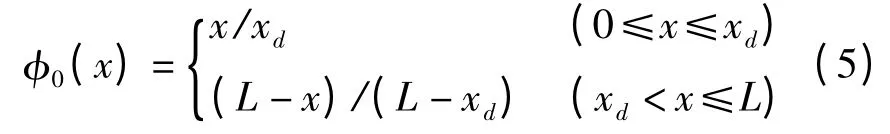
则斜拉索振动状态为

1.2.2 系统状态空间方程表达

式中 zq(t)——y 向广义坐标状态变量

A——系统矩阵

B——控制矩阵

D——扰动矩阵

同时，φi(x)需满足索的几何边界条件φi(0)=φi(1)=0，φd=φ(xd)，φ0=φ(x0)。对此，引入状态矩阵与矩阵不确定性项［9］，式(7)改写为

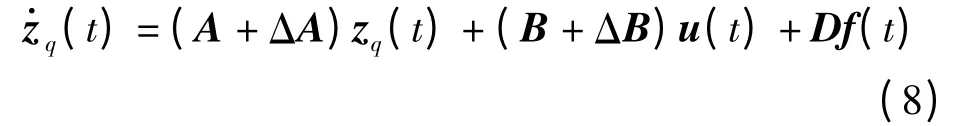
其中

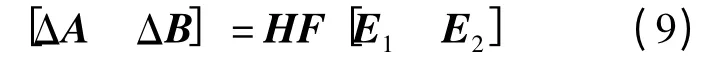
式中 ΔA——系统矩阵中未知实矩阵

ΔB——控制矩阵中未知实矩阵

F——不确定矩阵，∈Rij且满足FFT＜I

E1、E2——系统模型中不确定性结构矩阵

H——有LEBESUGE 可测元的未知矩阵

为解决斜拉索-磁流变阻尼器状态空间式(8)中减振控制器参数摄动问题，选用非脆弱状态反馈控制，即

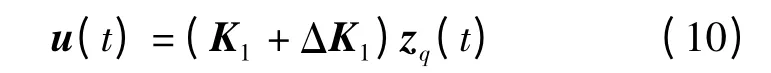
式中 K1——控制增益，∈Rm×n

ΔK1——控制器参数的增益摄动，∈Rm×n

为构造控制器增益摄动，选择加法摄动方式，其表达形式为

即斜拉索-磁流变阻尼器系统式(8)在非脆弱状态反馈控制式(10)作用下，得到系统状态方程

其中

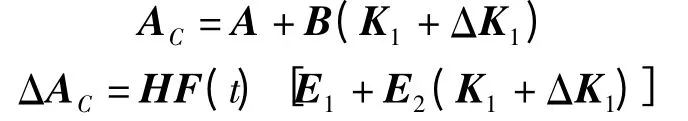
式中 WK(t)——外部激励载荷f(x)的函数［14］

基于此，设计一种多性能指标约束下的非脆弱减振控制器式(10)，其闭环系统的极点能够配置在以(-q，0)为圆心、半径为r 的圆盘区域F(-q，r)内，且满足0 ＜r ＜q，以保证减振控制快速性与稳定性;同时，为解决减振控制系统外界干扰及增益摄动问题，引入非脆弱控制、H∞性能指标约束、协方差性能指标约束，用以减少斜拉索的振幅与振速，且使振幅、振速稳态协方差矩阵X 有较小上界。若斜拉索-磁流变阻尼器减振控制系统稳定，则稳态协方差可定义为

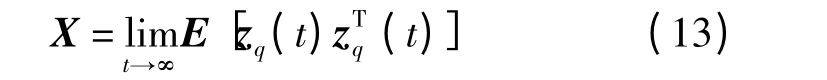
式中 X——半正定矩阵

且满足

结合引理，用以设计多性能指标约束的非脆弱减振控制器

引理1［15］:给定矩阵A，其所有特征值均在圆盘F(-q，r)中的充要条件是存在适维对称正定矩阵X ＞0，使得

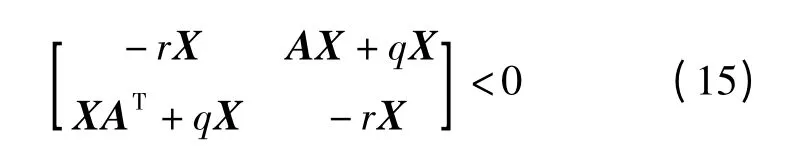
引理2［16］:给定适维矩阵Q、H、E，对任意满足FFT≤I 的矩阵F 存在

当且仅当存在正实数ε 使得

2 减振控制器设计

2.1 常规减振控制器

定理1:对随机载荷f(t)激励下的减振控制系统式(12)，不考虑控制器摄动，能使得控制器u(t)=K1zq(t)闭环系统极点配置在圆盘区域F(-q，r)内，且振幅、振速稳态协方差矩阵X 有上界的充要条件是以下矩阵不等式组有可行解［18］。

显然，式(19)为保证闭环系统极点配置到圆盘F(-q，r)区域内，使得减振控制具有快速性与稳定性;式(19)保证了振幅与振速方差矩阵有上界，满足:X ＜Q。式(20)要求矩阵Q 为正定矩阵。

为便于求解式(18)～(20)矩阵不等式方程，利用矩阵变换和引理将其转换为下LMIs 形式。

定理2:减振控制器u(t)=K1zq(t)在随机载荷f(t)的激励下，存在反馈控制增益阵K1，使得减振控制系统极点配置在圆盘区域F(-q，r)内且振幅、振速稳态协方差矩阵X 有上界的充要条件是:存在正实数变量εi(i=1，2，3)和矩阵变量Q、S，使LMIs有可行解，即

证明:定义控制增益K1=SQ-1，应用引理1 ～3，并参照文献［19］，可知结论成立。

2.2 H∞减振控制器

定理3:减振控制器u(t)=K1zq(t)在随机载荷f(t)激励下，减振控制器极点能够配置在圆盘区域F(-q，r)内，系统抗干扰能力‖H(S)‖∞＜γ，且振幅、振速稳态协方差矩阵X 有上界的充要条件是存在可配置正定矩阵Q 和反馈增益K1同时满足［20］

式(24)～(27)分别表示闭环系统极点配置到圆盘F(-q，r)区域内，以保证减振控制具有快速性与稳定性;系统抑制外界干扰指标‖H(S)‖∞＜γ;以及斜拉索的振幅与振速稳态状态协方差阵有上界且X ＜Q。

利用矩阵变换和引理将其转换为下LMIs 等价形式。

定理4:减振控制器u(t)=K1zq(t)在随机载荷f(t)的激励下，存在反馈控制增益阵K1，使得减振控制系统极点配置在圆盘区域F(-q，r)内，系统抑制外界干扰指标‖H(S)‖∞＜γ，且振幅、振速稳态协方差矩阵X 有上界的充要条件是:存在正实数变量εi(i=1，2，3，4，5)、γ 和矩阵变量Q、S，使线性LMIs 有可行解，即

证明:略。

2.3 非脆弱减振控制器

定理5:减振控制闭环系统式(12)在随机载荷f(t)的激励下，控制器参数具有一定的摄动范围，闭环极点配置在圆盘区域F(-q，r)内，且振幅、振速稳态协方差矩阵X 有上界，同时，能够抑制系统外界干扰指标‖H(S)‖∞＜γ 的条件为存在可配置正定矩阵Q 和非脆弱减振控制增益，同时满足［21］

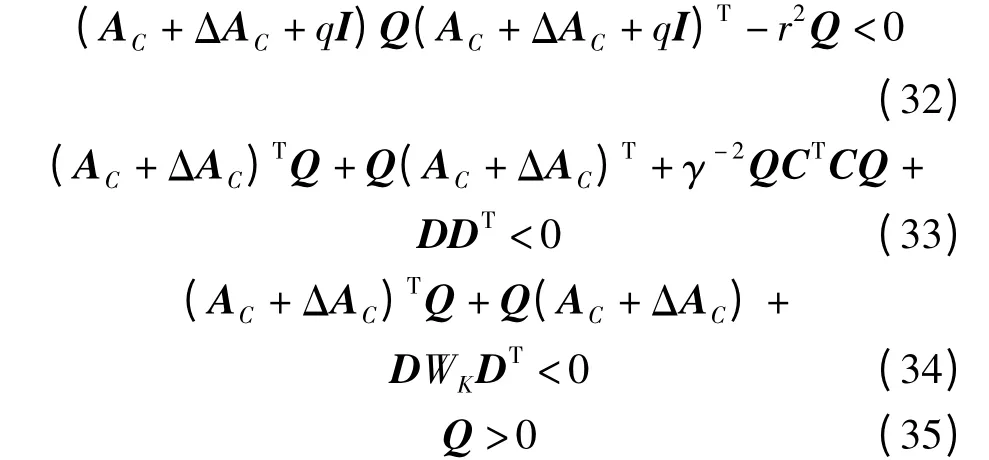
式(32)～(35)分别表示必存在正定矩阵Q 和非脆弱减振控制器反馈增益=K1+ΔK1，使减振控制系统中的实常数方阵A 的所有特征值均具有负实部，且可配置到圆盘区域F(-q，r)内，以保证减振控制具有一定的快速性与稳定性;同时，为抑制外界干扰和斜拉索的振幅、振速，其对应的闭环系统满足‖H(S)‖∞＜γ，振幅、振速稳态状态协方差矩阵X和正定矩阵Q 之间的关系也必满足X ＜Q。

为便于求解，利用矩阵变换和引理将上述矩阵不等式转换为下LMIs 等价形式。

定理6:若斜拉索-磁流变阻尼器减振控制器式(10)中含有加性不确定性式(11)，则闭环系统式(12)极点配置于圆盘区域F(q，r)内且满足振幅、振速稳态协方差矩阵X 有上界，同时，能够抑制系统外界干扰指标‖H(S)‖∞＜γ 的充要条件为:存在正实数变量εi(i =1，2，…，7)、γ 和矩阵变量Q、S，使得LMIs 有可行解，即

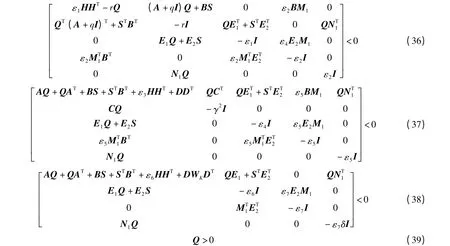
式中，S=K1Q，则在含有加性不确定摄动系统式(11)中，其名义控制增益为K1=SQ-1。

证明:根据引理1、引理2，表征快速性与稳定性圆盘极点约束性能指标式(32)等价为

由引理(2)可得

令S=K1Q，根据引理3 可证得与不等式(32)等价条件式(36)。此外，为抑制外界对减振控制系统干扰，引入H∞性能指标约束式(33)，并结合引理1 ～3，可证得等价条件式(37)。同理可证斜拉索振幅、振速稳态协方差约束式(34)等价于式(38)。

若要进一步优化减振控制器增益及抑制扰动的H∞性能指标γ，需结合凸优化方法，以解决系统H∞性能指标γ、圆盘极点可配置、振幅和振速稳态协方差性能指标约束下的极小值问题。

2.4 凸优化问题求解

假设在非脆弱控制下能同时满足H∞性能指标约束、圆盘极点性能指标约束和方差性能指标约束，由定理6 可知，式(36)～(39)必有可行解，其不仅使H∞性能指标γ 较小，且其稳态状态方差性能指标的上界与极点性能指标有相容的较小上界［22］，即

令(QL，SL，ε1L，ε2L，…，ε7L，γ2L)为上述极值问题的相应极小值，若给定方差上界σ2＞diag(QL)，则式(36)～(39)必有可行解。于是，在给定H∞性能指标γ、极点配置性能指标和方差上界性能指标σ2＞diag(QL)时，则定理7 成立。

定理7:若减振控制器闭环系统式(12)极点可配置，取H∞性能指标γ、圆盘极点性能指标以及振速、振幅稳态协方差性能指标，则满足σ2＞diag(QL)的方差上界指标σ2与区域极点指标F(- q，r)相容，即

3 仿真实例

3.1 系统状态空间方程矩阵参数

以浙江省某跨海大桥C22(长索)和C13(短索)斜拉索为实例验证。磁流变阻尼器安装方式如图1所示。斜拉索与MR-60 型磁流变阻尼器相互垂直于连接处，且对称安装在距离桥面高1.8 m 位置。

MR-60 型磁流变阻尼器最大工作电流为2 A，最大阻尼力为8 kN，部分工况参数［23］如表1 所示。

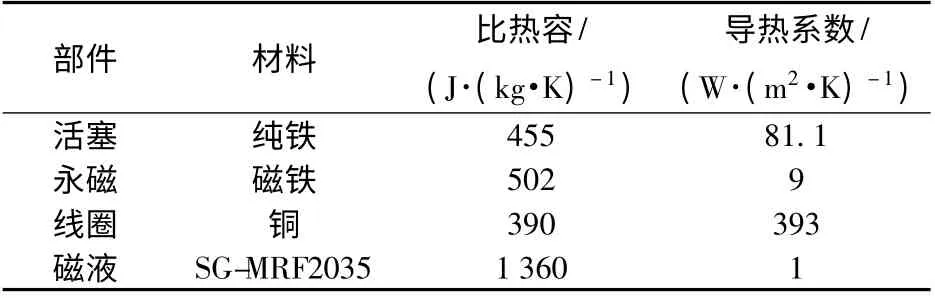
表1 MR-60 型磁流变阻尼器工况参数Tab.1 Working parameters of MR-60 magnetorheological damper

斜拉索材料选用镀锌钢丝，其弹性模量为200 GPa，C22 和C13 斜拉索基本参数如表2、3 所示。

表2 C22 斜拉索基本参数Tab.2 Basic parameters of C22 stay cable

表3 C13 斜拉索基本参数Tab.3 Basic parameters of C13 stay cable

结合式(8)，取形函数数目n =2［9］，可计算得C22 和C13 号斜拉索参数矩阵M、K、C 和A、B、D及WK为

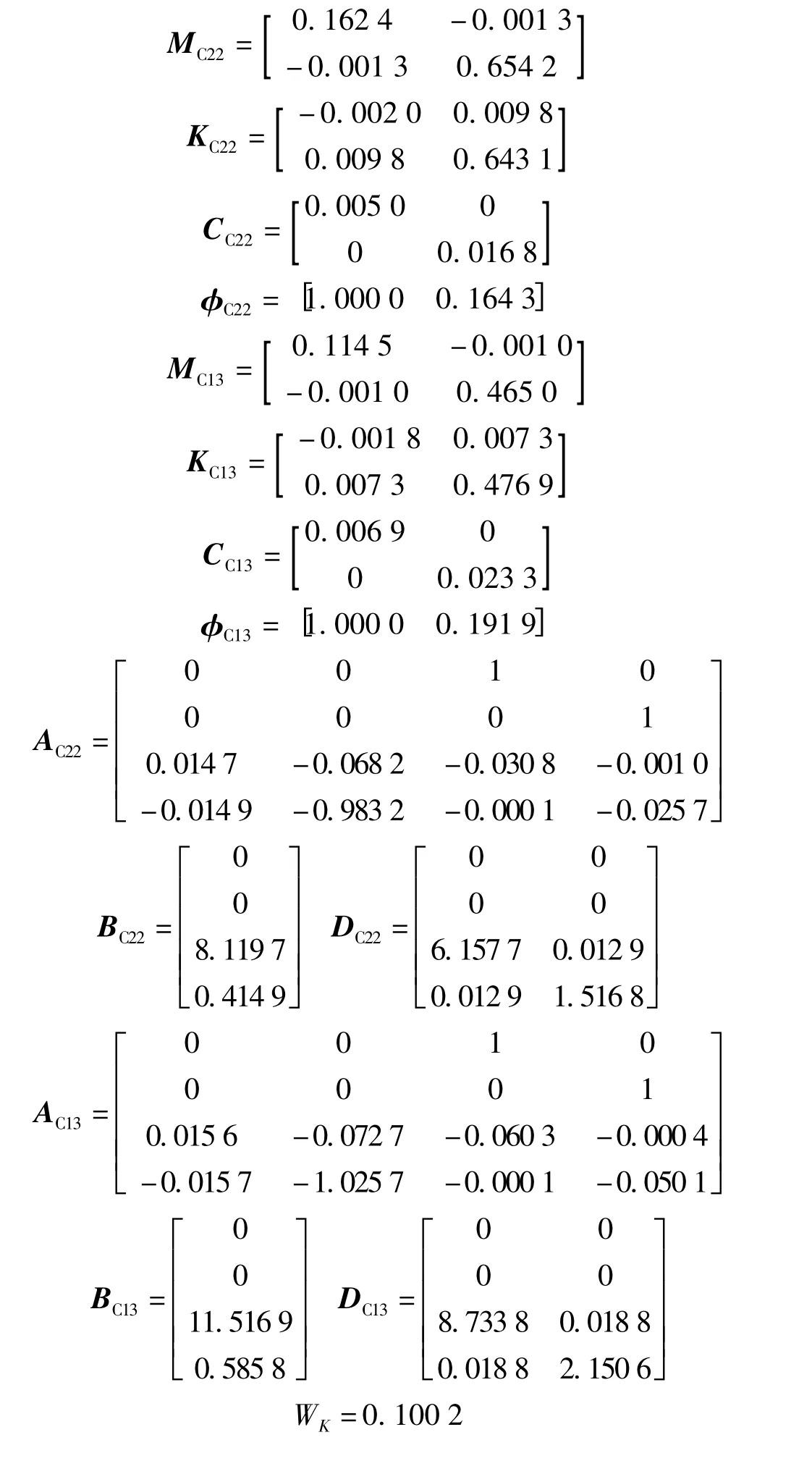
3.2 系统不确定参数及控制器增益摄动不确定性参数

考虑到实际的工程环境、斜拉索模型的非线性和增益摄动范围等因素，引入5%不确定性误差作为模型输入矩阵和控制器参数摄动误差，则

由于非脆弱减振控制器增益K*1在实际执行时为［24-25］

其中

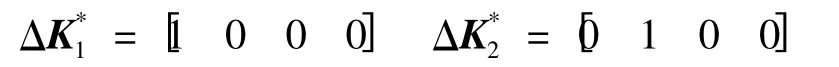
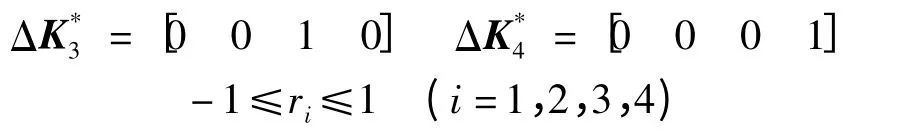
则可定义矩阵

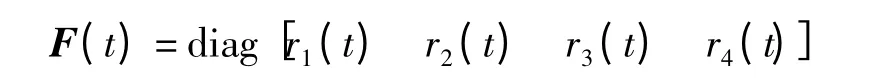
同时，考虑到5%输入误差，则取

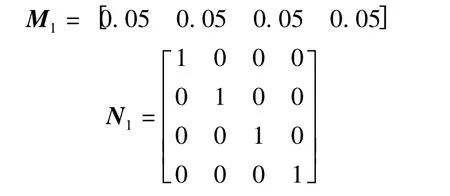
利用Matlab 并结合定理2、定理4、定理6、定理7可得C22、C13 号斜拉索相应控制器增益及抗扰指标γ。

常规减振控制器增益为:K1C22=［-0.431 6 0.026 5 -0.500 9 -0.068 0］;K1C13=［-0.328 9 0.011 4 -0.360 5 -0.040 7］。

H∞减振控制器增益及抗扰指标γ 为:K2C22=［-0.417 5 0.007 8 -0.495 2 -0.051 4］;K2C13=［-0.348 1 0.001 4 -0.366 7 -0.033 0］;γC22min=2.121 4、γC13min=2.143 1，取H∞性能指标γC22=γC13=3。

非脆弱减振控制器增益及抗扰指标为:K3C22=［-0.512 5 -0.905 9 -0.566 4 1.151 1］;K3C13=［-0.387 3 -0.560 3 -0.410 4 0.673 9］;γC22min=1.251 9;γC13min=1.716 9，取H∞性能指标γC22=γC13=2。

非脆弱减振控制器控制下的极点与常规减振控制器、H∞减振控制器控制下的极点能够配置在同一圆盘F(-2，1)内，得到极点分布图如图2、3 所示。

图2 C22 号斜拉索3 种不同减振控制系统闭环极点分布图Fig.2 Closed-loop pole distribution of three different vibration damping control systems for C22 stay cable

图3 C13 号斜拉索3 种不同减振控制系统闭环极点分布图Fig.3 Closed-loop pole distribution of three different vibration damping control systems for C13 stay cable

以不同均值高斯白噪声(WK=0.100 2、2WK=0.200 4)分别表示不同随机载荷扰动，通过Simulink仿真计算，获得3 种不同减振控制器在不同随机扰动、不同振动状态下的零输入响应曲线，如图4、5所示。

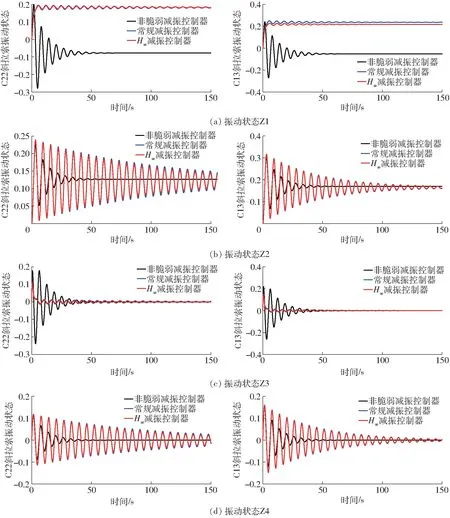
图4 随机扰动为0.100 2 时C22 号与C13 号斜拉索不同状态零响应输入曲线Fig.4 Zero response input curves of C22 and C13 stay cables with random disturbances at 0.100 2

由图4、5 可知，常规减振控制器指仅含极点配置性能指标约束、稳态协方差性能指标约束的闭环控制系统;H∞减振控制器指同时拥有H∞性能指标约束、极点配置性能指标约束、稳态协方差性能指标约束的闭环控制系统;非脆弱减振控制器指闭环系统不仅满足H∞性能指标约束、极点配置性能指标约束、稳态协方差性能指标约束，且求取的反馈控制矩阵K1在一定的摄动范围内仍能使减振控制器闭环系统保持稳定。此外，Z1、Z2 表示系统在减振控制器作用下振动幅值的响应状态;Z3、Z4 表示系统在减振控制器作用下振动速度的响应状态。

3.3 仿真分析比较

通过对比H∞减振控制器及非脆弱减振控制器抗扰性能指标值γ 可知，非脆弱减振控制器闭环系统拥有较小的抗扰指标值。同时，由图2、3 分析可知，在非脆弱控制及多性能指标约束作用下(H∞性能指标约束、圆盘极点约束、稳态协方差性能指标约束)，非脆弱减振控制器闭环系统的极点与常规减振控制器闭环系统的极点、H∞减振控制器闭环系统的极点能配置在同一圆盘F(-2，1)内，使得系统的稳定性得以保证。

此外，由图4、5 知，在WK及2WK2 种强度的随机载荷扰动下，C22 号与C13 号斜拉索在H∞减振控制器控制下的不同振动状态比常规减振控制器控制下的振动幅值和振动速度的收敛时间有所降低，但减少量不太明显，且收敛时间均在150 s 后;而在非脆弱减振控制器控制下的不同振动状态的振动幅值和振动速度在70 ～80 s 内已收敛。同时，在WK=0.100 2 和2WK=0.200 4 随载荷扰动下，C22 号索振幅降低57.805%，收敛时间缩短56.705%;C13号索振幅降低74.395%，收敛时间缩短77.845%。