模拟翼型热敏介质空化流的湍流模型修正与应用
2020-07-07张德胜万福来李俊峰施卫东
张德胜 冯 健 万福来 李俊峰 施卫东
(1.江苏大学流体机械工程技术研究中心,镇江212013;2.南通大学机械工程学院,南通226019)
0 引言
空化是一种复杂的两相流动现象[1-3],普遍存在于多种流体机械中,例如水轮机、透平机、螺旋桨等。当流体机械内部的局部流体压力低于相应温度下的饱和蒸汽压时,就会产生空化。空化会造成较大的振动和噪声,损坏过流部件,加剧轴承的磨损,影响流体机械的使用寿命。
湍流模型在空化问题的研究中起着重要作用。目前,基于雷诺时均方程的模拟方法被广泛应用于空化数值模拟中。文献[4]采用SST k-ω 湍流模型进行数值模拟,并结合实验分析了高速诱导轮离心泵内的空化特性。文献[5]采用RNG k-ε 湍流模型分析了不同空化数下翼型的云状空化脱落特性。近年来,随着计算流体力学的快速发展,一些学者采用大涡模拟(Large eddy simulation,LES)研究瞬态流动特性[6-8],大涡模拟可以直接模拟大尺度湍流流动,利用次网格尺度模型模拟小尺度湍流流动对大尺度湍流流动的影响,在实际工程中得到一定应用。目前,有关湍流模型对空化流模拟影响的研究主要以常温水为工作介质,常温水的饱和蒸汽压强随温度变化梯度较小,其空化过程可视为等温过程,而高温水、液化天然气、液氢等介质的饱和蒸汽压强对温度变化敏感,属于热敏介质,其空化过程不可视为等温过程。一些学者着重分析了空化模型对热敏介质空化流的影响[9-10],而针对湍流模型对热敏介质空化流模拟影响的研究较少。
本文结合FBM 模型和DCM 模型,对现有3 种湍流模型(k-ε、RNG k-ε 和SST k-ω)进行修正,并对不同温度水绕NACA0015 翼型进行空化模拟,结合实验对比验证修正模型的数值模拟精度。
1 控制方程与数值方法
1.1 基本方程
本文采用均质平衡流模型模拟气液两相空化流动,该模型将气液混合物的密度看成均匀单一的密度,并且混合物具有相同的流速和压力。基本控制方程包括连续性方程、动量方程和能量方程,依次表示为

其中

式中 ρm——混合介质密度,kg/m3
ρl——液相密度,kg/m3
ρv——气相密度,kg/m3
u——速度,m/s
αv——气相体积分数
p——压力,Pa
μ——混合介质层流粘度,Pa·s
μt——混合介质湍流粘度,Pa·s
h——焓,J
L——液体的气化潜热,kJ/kg
fv——气相质量分数
PrL——层流普朗特数
Prt——湍流普朗特数
t——时间,s
δij——克罗内克函数
下角标i、j、k 表示坐标方向。
1.2 湍流模型
湍流模型可以分成两方程模型、一方程模型和零方程模型。本文主要针对两方程模型中的3 种湍流模型(k-ε、RNG k-ε 和SST k-ω)进行修正和对比分析。
1.2.1 k-ε 湍流模型
Launder 和Spalding 在1972 年提出了k-ε 湍流模型,需要求解两个附加方程,通过求解湍动能和湍动能耗散率来求解湍流粘度,以此得到湍流应力。
湍动能k 方程为

式中 σk——湍动能的湍流普朗特数Gk——湍流动能
湍动能耗散率ε 方程为

式中 σε——耗散率的湍流普朗特数经验系数Cε1、Cε2分别取1.44 和1.92。
湍流粘度μt方程为

式中 Cμ——经验系数
1.2.2 RNG k-ε 湍流模型
RNG k-ε 湍流模型[11]考虑了平均流动中的旋转流动情况,在湍动能耗散率ε 方程中添加一项,反映了时均应变率Eij。
湍动能k 方程为

式中 αk——经验系数,取1.393
μeff——有效粘度,Pa·s
湍动能耗散率ε 方程为

其中
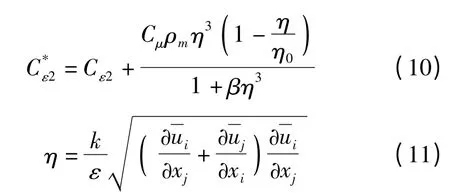
式中 αε——经验系数
经验系数分别为:αε=1.393,Cε1=1.42,Cε2=1.68,Cμ=0.084 5,η0=4.38,β=0.012。
1.2.3 SST k-ω 湍流模型
SST k-ω 湍流模型[12]结合k-ω 模型和k-ε 模型,近壁面处采用k-ω 模型计算低雷诺数问题,在远壁处采用k-ε 模型计算。
湍动能k 方程为

式中 Pk——湍流生成速率
β′——经验系数,取0.09
湍流频率ω 方程为

涡流粘度νt方程为

式中 S——固定应变率估计值
F1、F2——混合函数
经验系数分别为:α1= 0.3,α = 5/9,σω2=1/0.856。
1.3 湍流模型修正
文献[13]考虑气液两相混合密度的可压缩性对湍流粘度的影响,提出采用DCM 模型修正湍流粘度,公式为

其中

根据文献[13],n 取10。
文献[14]提出一种FBM 模型,保证运输方程不变的情况下,在湍流粘度中引入一个滤波函数fFBM,公式为

其中

式中 C3——经验系数,取1.0
Δ——滤波尺寸,其值取决于网格尺寸
结合滤波器模型与密度修正模型对湍流粘度进行修正[15],公式为

其中


式中,χ 指函数符号,根据文献[15],经验系数C1、C2、C3、C4分别取4、0.2、0.6、0.2。
1.4 Merkle 空化模型
Merkle 空化模型[16]推导了气液混合物中的相间传质方程。气相体积分数输运方程和蒸发凝结源相表达式为

其中
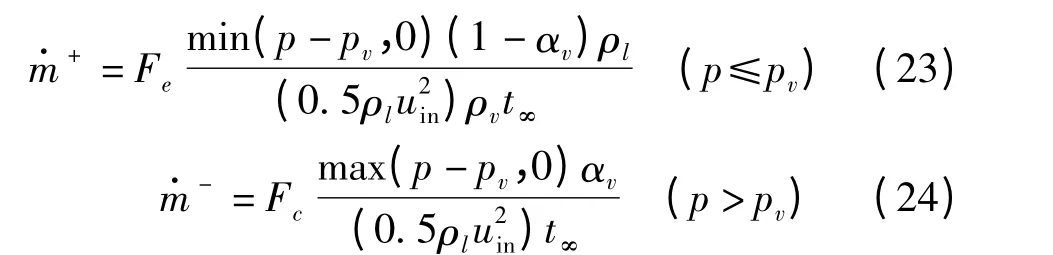
式
中 Fe、Fc——蒸发、凝结系数,取1、80 u
in——进口速度,m/s
t∞——特征时间,s
pv——饱和压力,Pa
1.5 数值设置与验证
文献[17]对不同温度水绕NACA0015 翼型进行了系统的空化实验研究,分析了热力学效应对空化性能的影响。实验用的NACA0015 翼型结构如图1 所示。实验段进出口各设有3 个测压孔,翼型吸力面设有10 个测压孔,压力面设有2 个测压孔。
考虑到流动的充分发展以及稳定性,对计算域适当延伸,进口与出口分别延伸至2 倍与4 倍翼型弦长,翼型攻角为5°,三维模型如图2 所示。

图1 结构示意图Fig.1 Schematic of test section

图2 NACA0015 翼型三维模型Fig.2 3D model of NACA0015 hydrofoil
边界条件设置与实验对应:进口设置为速度入口,出口设置为压力出口,壁面设置为无滑移边界。不同温度水下的进出口参数值如表1 所示。
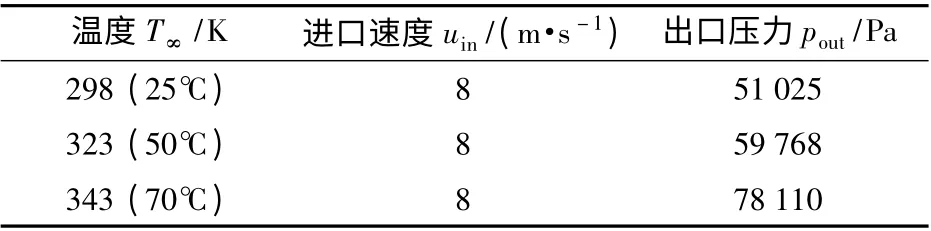
表1 边界条件Tab.1 Boundary conditions
本文采用ICEMCFD 软件对NACA0015 翼型划分六面体结构网格,计算域网格如图3 所示。翼型边界层网格质量对数值计算精度有较大影响,通常采用y+来验证网格质量是否达到计算精度要求。大多数学者采用的y+范围为60 以下,此范围内得到的结果与实验值较为吻合[18-19]。为提高翼型网格质量,对翼型前缘采用C 型网格划分,并对翼型前缘和尾缘部分进行网格加密,如图4 所示。调整后的翼型上、下表面y+分布如图5 所示,其中Lc为翼型长度百分比。采用3 组不同加密程度的网格,在定常无空化工况下,以25℃水为介质,进行绕NACA0015 翼型数值计算。运用无量纲压力系数Cp与实验结果[17]对比,公式为

图3 NACA0015 翼型网格Fig.3 Mesh of NACA0015 hydrofoil

图4 前缘和尾缘网格分布Fig.4 Mesh distribution of leading edge and trailing edge

图5 NACA0015 翼型y +分布Fig.5 Distribution of NACA0015 hydrofoil

计算结果如图6 所示,3 组网格节点数分别为114 万(方案1)、285 万(方案2)和456 万(方案3)。计算结果表明3 组方案的模拟压力系数与实验值吻合度较高,结合网格实用性与计算成本,选取方案2作为本文的研究方案。
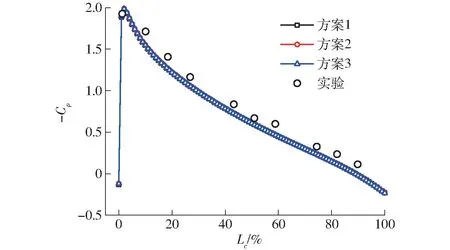
图6 网格无关性验证Fig.6 Verification of mesh independence
2 结果与讨论
2.1 25℃时湍流模型
采用3 种湍流模型以及修正后的湍流模型,进行常温下绕NACA0015 翼型的非空化单相数值模拟,得到翼型吸力面的压力系数分布,如图7(图中FBDCM 表示修正模型)所示。结果表明,采用修正前后的湍流模型得到的计算结果相差不大,均与实验值比较接近,验证了网格和湍流模型的适用性。

图7 25℃时非空化工况下NACA0015 翼型表面压力系数分布Fig.7 Pressure coefficient distribution of NACA0015 hydrofoil on non-cavitation at 25℃
采用3 种湍流模型以及修正后的湍流模型,在常温下,绕NACA0015 翼型进行空化气液两相数值模拟,图8 给出了翼型吸力面的压力系数分布。结果表明,修正前3 种湍流模型的计算结果与实验值在翼型长度前30%的低压区存在一定误差,压力开始恢复的起点均早于实验结果,在空化核心区域,模拟压力系数与实验压力系数存在误差。在翼型长度后70%段,RNG k-ε 与SST k-ω 湍流模型的计算结果更接近实验值,k-ε 模型的模拟结果与实验结果相差较大;修正后的RNG k-ε 模型与修正后的SST k-ω 模型的计算结果得到明显的改善,压力恢复起始点与实验值较为接近,而修正后的k-ε 模型模拟结果与修正前相比误差明显减小,修正效果较为明显。这是因为两方程湍流模型模拟空化流动时,计算的气液混合区的湍流粘度过大,造成过高的能量耗散,影响空化模拟的准确性,而FBDCM 模型通过分域函数结合FBM 模型和DCM 模型,在不同的区域采用不同的方式修正湍流粘度,提高了空化模拟的准确性。

图8 25℃时空化工况下NACA0015 翼型表面压力系数分布Fig.8 Pressure coefficient distribution of NACA0015 hydrofoil on cavitation at 25℃
图9 给出了常温下3 种湍流模型修正前后模拟得到的翼型表面蒸汽体积分数分布。可以看出,k-ε模型在空穴尾部的闭合区域出现较大尺度涡,空化核心区域发展过程较长,而RNG k-ε 与SST k-ω 模型在空化核心区域发展过程较短。3 种湍流模型在修正前与实验结果均存在一定误差,其中k-ε 模型的模拟结果误差最大。修正后的k-ε 模型消除了kε 模型空穴尾部闭合区域的涡,但空化核心区域长度较修正前明显减小。修正的RNG k-ε 模型与修正的SST k-ω 模型计算得到的空化核心区域较修正前明显扩大,与实验结果更接近,但空化核心区域蒸汽体积分数增大,空化程度更严重。原因为k-ε 模型中引入的耗散率ε 方程是由经验方法得到的,不是由推导所得,并且采用的3 种湍流模型中只有k-ε模型没有考虑应变率的影响,不能反映时均应变率,导致在空穴尾部区域具有较大的压力梯度与大曲率流动的情况下,k-ε 模型的模拟精度较差。采用FBDCM 模型修正各湍流模型后,降低了空穴区域的湍流粘度,减少了能量耗散,空化流场得到发展。
2.2 50℃时湍流模型
根据上述讨论,修正的RNG k-ε 模型与修正的SST k-ω 模型具有较好的适用性,故本节主要采用修正后的RNG k-ε 模型与修正后的SST k-ω 模型对NACA0015 翼型以50℃水为介质进行空化数值模拟分析。
图10 给出了修正的RNG k-ε 模型与修正的SST k-ω 模型模拟所得的NACA0015 翼型吸力面的压力分布。结果表明,在空化核心区域,两种模型计算得到的压力均低于实验值,空化现象较实验结果更为严重。修正的SST k-ω 模型的计算结果与实验结果较符合,但压力恢复阶段的梯度与实验结果相比较大。

图9 25℃时NACA0015 翼型表面蒸汽体积分数分布Fig.9 Vapor volume fraction distributions on surface of NACA0015 hydrofoil
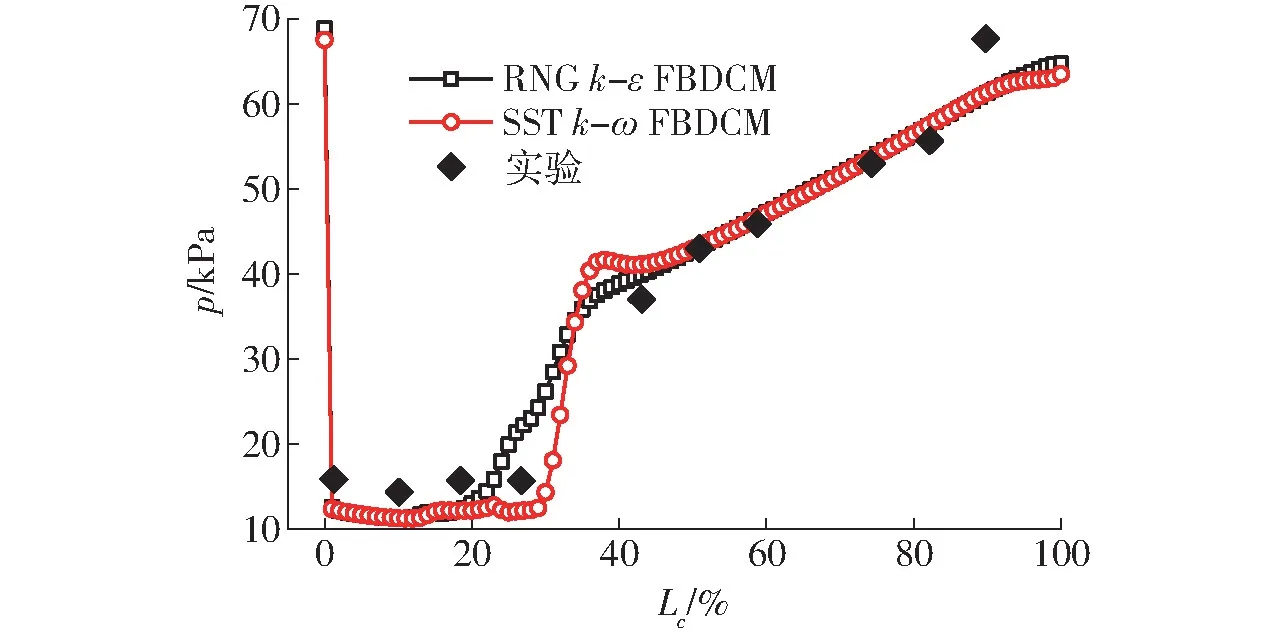
图10 50℃时翼型表面压力分布Fig.10 Pressure distribution of hydrofoil at 50℃
图11 为50℃时修正的RNG k-ε 模型与修正的SST k-ω 模型得到的翼型表面相间质量传输速率分布,其中蒸发过程为正值,凝结过程为负值。结果表明,修正的SST k-ω 凝结速率明显大于修正的RNG k-ε 凝结速率,但修正的SST k-ω 凝结区域明显小于修正的RNG k-ε 凝结区域。此外,与修正的SST k-ω模型相比,修正的RNG k-ε 模型凝结起始点位置更靠近翼型头部。在50℃时,两种模型的模拟结果与实验结果均有一定误差。
2.3 70℃时湍流模型
图12 为70℃时修正的RNG k-ε 模型与修正的SST k-ω 模型模拟得到的NACA0015 翼型吸力面压力系数分布图。结果表明,两种湍流模型计算得到的空化核心区域范围均比实验结果大,但修正的RNG k-ε 模型模拟得到的空泡生成和溃灭趋势与实验结果较为一致,修正的SST k-ω 模型空化发展过程较长,在压力恢复阶段梯度较大。
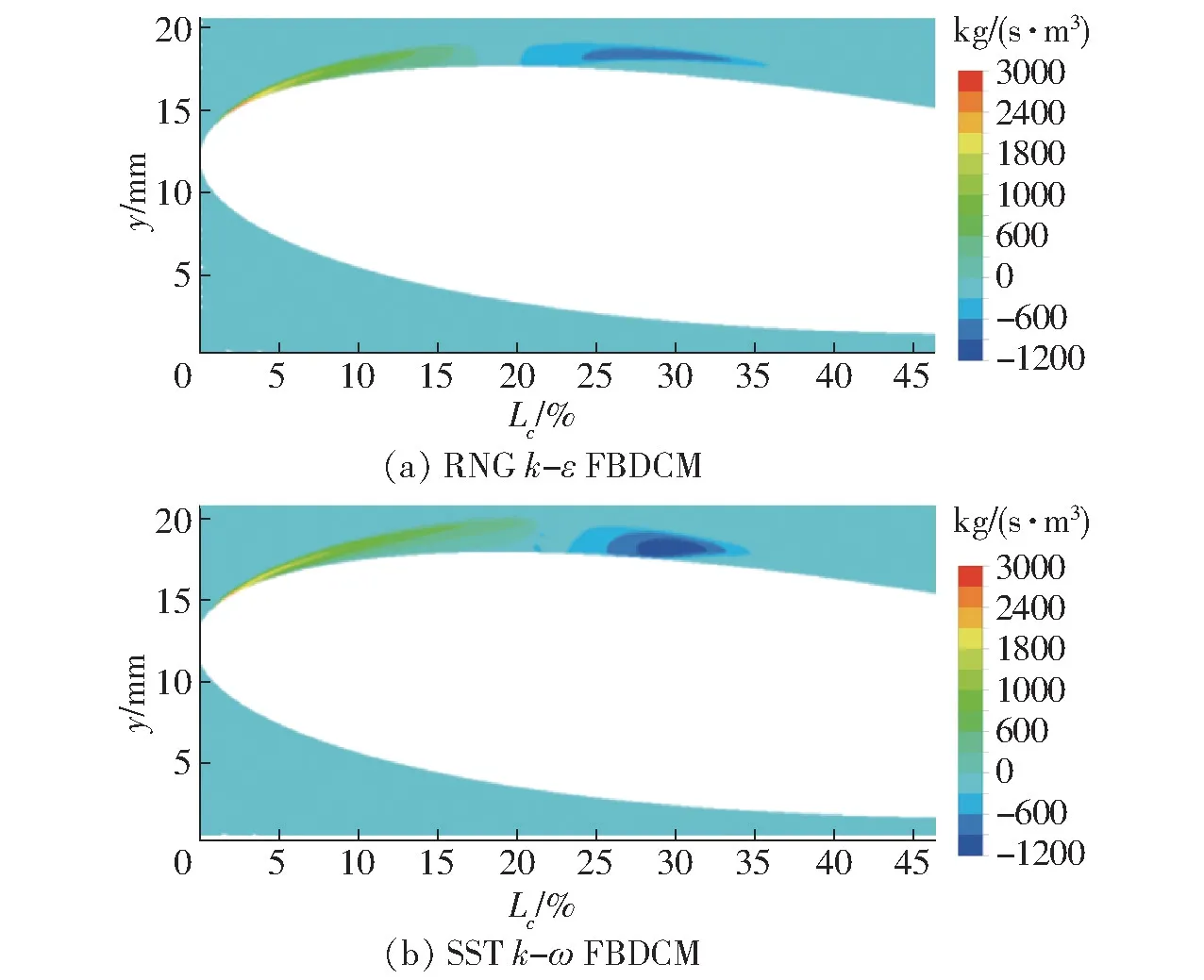
图11 NACA0015 翼型表面相间质量传输速率分布Fig.11 Bulk interphase mass transfer rate distributions on surface of NACA0015 hydrofoil
图13 给出了70℃时修正的RNG k-ε 模型与修正的SST k-ω 模型模拟得到的NACA0015 翼型表面湍动能分布情况。结果表明,修正的SST k-ω 模型计算所得湍动能明显大于修正的RNG k-ε 模型计算所得湍动能,近壁处流动较为紊乱,并且空化更加严重,与实验所得结果相差较大。
2.4 修正的RNG k-ε 模型
为了分析不同水温下的翼型空化特性,定义了无量纲空化数

图12 70℃时翼型表面压力系数分布Fig.12 Pressure coefficient distribution of hydrofoil at 70℃

式中 pin——进口压力
图14 为在相同空化数(σ=1.5),不同水温下,由修正的RNG k-ε 模型计算得到的翼型表面蒸汽体积分数分布图。结果表明:随着温度的升高,蒸汽体积分数减小,空化强度下降,空穴面积减小,空穴尾端闭合区域的逆压梯度减小,气液界面变得模糊[20-23]。由于温度的升高,水蒸气含量降低,气液混合区密度增大,气液界面密度梯度增大,导致气液界面模糊[24-26],说明随着温度的升高,水的热力学效应抑制空化的效果更加明显,空化强度相对减弱,这与实验观察到的规律相一致。

图13 NACA0015 翼型表面湍动能分布Fig.13 Turbulence kinetic energy distribution on surface of NACA0015 hydrofoil

图14 NACA0015 翼型表面蒸汽体积分数分布Fig.14 Vapor volume fraction distributions on surface of NACA0015 hydrofoil
3 结论
(1)3 种方案的计算结果均与实验结果吻合较好,同时验证了网格的无关性。在常温非空化条件下,修正前后3 种湍流模型的计算结果与实验结果一致。
(2)25℃时,修正的k-ε 模型对湍流尺度具有明显的修正效果,空泡尾部闭合区域的涡被消除,修正的RNG k-ε 模型与修正的SST k-ω 模型的模拟结果在空化区域与实验结果较为接近。50℃时,在蒸发过程中由修正的RNG k-ε 模型计算得到的蒸发区域较小,而在凝结过程中由修正的SST k-ω 模型计算得到的凝结速率较大。70℃时,修正的SST k-ω模型在近壁处的湍动能明显大于修正的RNG k-ε模型的结果,空化程度更严重,与实验结果相差较大。
(3)在不同温度、相同空化数下,修正的RNG k-ε模型揭示了NACA0015 翼型空化情况随温度的变化规律,并且与实验观察结果相一致,验证了修正的RNG k-ε 模型准确性。
(4)对3 种温度下湍流模型修正前后的结果进行了综合分析,并与实验结果进行了比较。结果表明,修正的RNG k-ε 模型对于热敏介质的气液两相流模拟具有较好的适用性。
