基于PROSAIL 模型偏差补偿的水稻叶绿素含量遥感估测

刘 潭 许童羽 于丰华 袁青云 郭忠辉 王永刚

(1.沈阳农业大学信息与电气工程学院，沈阳110866;2.辽宁省农业信息化工程技术研究中心，沈阳110866)

0 引言

水稻是我国主要粮食作物之一，水稻叶绿素含量是衡量其长势的重要指标，实现水稻叶绿素含量的精准估测对其长势监测、施肥施药调控及田间的精准管理具有重要意义。近年来，高光谱遥感技术为实现作物叶绿素等含量监测提供了一种有效的手段［1-2］。

目前，基于高光谱信息估测水稻等作物叶绿素含量的方法主要包括两类:一类是利用光谱波段组合生成的各种光谱指数，如比值指数(RVI)、三角植被指数(TVI)、土壤调整植被指数(SAVI)、绿波段归一化植被指数等［3］，这些指数与叶绿素含量之间有较好的相关性。另一类是利用光谱特征变量，如利用归一化光谱的反射峰与吸收谷等特征变量，或利用基于导数光谱的特征变量来度量叶绿素的变化。

在水稻等作物叶绿素含量反演建模方面，已有模型大多基于自变量与因变量之间为线性关系的假设［4］，如一元线性、多元线性模型等。数据的线性特征可以通过数学转换来实现，但是那些具有复杂非线性特征的数据却难以通过数学转换来实现。因此，基于机器学习的非线性建模方法逐渐被应用到估测叶绿素含量上。

文献［5 -8］中模型均属于数据模型，此类模型通常结构简单、分析方便。数据模型通常是在特定的空间和时间下确定的，且随着观测集合信息等变化而变化，限制了其应用范围。为了提高模型的普适性［9］，一些学者致力于机理模型的研究。如LI等［10-11］结合农学知识，将PROSAIL 模型应用于作物监测中，证明其在预测叶绿素含量等参数上的优势。SUN 等［12］利用PROSPECT 模型反演估测作物叶片叶绿素状况。杨曦光等［13］和董晶晶等［14］利用辐射传输模型模拟植被冠层光谱反射率，通过分析模拟数据的叶绿素含量以及冠层光谱之间的关系，构建了估测植被叶片及冠层水平叶绿素含量的光谱指数模型。这些研究表明，机理模型物理意义明确，且反演过程较为稳定，适应性较好。由于作物叶绿素含量与其影响因素之间的关系复杂，相应的参数和变量较多，且地表环境系统包含众多不确定性因素，故机理建模只能在一定假设和简化下进行，导致不可避免地存在模型偏差［15］。

目前，针对整个生育期内动态监测水稻长势的研究较少，现有方法估测叶绿素含量通常基于某一特定生育期，不能覆盖整个或多个水稻生育期［16］。水稻长势直接影响水稻产量，因此，选择合适的建模方法，建立多个生育期内的水稻叶绿素含量估测模型，实时监测水稻长势，对农业生产及决策具有重要指导意义。

综合以上数据模型和机理模型的优点，在关键生育期内，将数据模型和机理模型相结合，本文提出一种水稻叶绿素含量估测的混合建模方法。利用PROSAIL 辐射传输模型模拟冠层光谱，建立查找表，初步反演水稻叶绿素含量，并采用LSSVM 方法建立数据补偿模型，弥补PROSAIL 机理建模存在的偏差，为利用高光谱信息估测水稻叶绿素含量提供新的研究思路和方法。

1 材料与方法

1.1 研究区概况

试验于2017 年5—10 月在辽宁省沈阳市沈阳农业大学道南试验田(41°49'N，123°33'E，平均海拔65 m)开展。该地区属于北温带半湿润大陆性气候，四季分明，降水集中，日照充足。试验地区年平均气温6.2 ～9.7℃，雨水主要集中在7、8 月，全年降水量为600 ～800 mm，粮食作物以东北粳稻为主。供试品种为沈稻47，进行小区栽培试验，种植18 个小区，单个试验小区面积为40 m2(5 m×8 m)。水稻插秧时间为5 月27 日，株距10 cm，设置4 个氮素水平:0、225、450、675 kg/hm2，每个水平设置3 个重复。在施肥过程中，氮肥分3 次施入，分别为基肥50%、分蘖肥20%、穗肥30%。另外，施用过磷酸钙510 kg/hm2作为基肥，硫酸钾150 kg/hm2作为穗肥。

1.2 数据采集

1.2.1 冠层光谱测定及数据处理

光谱测量采用美国ASD 公司的Analytical Spectral Devices 光谱仪，在水稻生长的分蘖期(6 月5 日)、拔节孕穗期(7 月5 日)、抽穗灌浆期(8 月8日)和成熟期(9 月18 日)，选择天气晴朗、无云、无风的气象条件下进行，并于10:00—14:00 测量水稻冠层光谱反射率。测量时，传感器探头向下，与水稻冠层顶端垂直距离约为1 m。在每个试验小区中心点附近选4 个不同位置，记录冠层光谱信息，将4 次测量结果的平均值作为该采样点的光谱反射值。并将相应的采样样本装入密封袋带回实验室进行叶绿素提取。为保证结果的准确性，每次测量都及时进行白板校正。为尽量消除光谱噪声，将400 nm以下噪声影响较大波段、1 000 nm 以上因水分吸收导致光谱不连续波段截去，因此本研究采用常用波段为400 ～1 000 nm，并将选取波段进行5 点平滑处理及归一化处理。

1.2.2 水稻叶绿素含量测定

采用Spectrum752 型紫外可见分光光度计测定叶绿素含量。将丙酮、无水乙醇、蒸馏水按体积比9∶9∶2配成混合溶液，选择若干水稻不同部位的完全展开叶片，剪碎后相互混合均匀，称取0.4 g 加入200 mL 混合溶液浸泡，待叶片完全变白后测定663、645 nm 波长处的光密度，测量3 次取平均值，根据光密度计算叶绿素质量浓度，计算式为

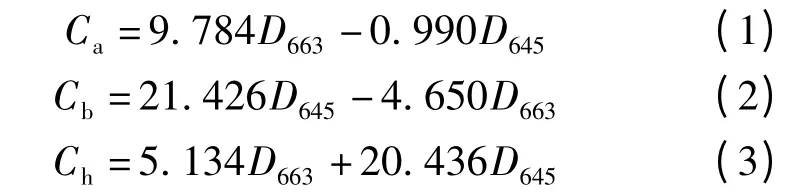
式中 Ca、Cb——叶绿素a 和叶绿素b 质量浓度，mg/L

Ch——叶绿素总质量浓度，mg/L

D663、D645——波长663、645 nm 处光密度，%

为了与PROSAIL 模型反演输出的叶绿素浓度保持一致，获得叶绿素浓度后需换算成单位面积内叶绿素含量Cab［17］。

1.3 PROSAIL 模型及其敏感性分析

PROSAIL 模型是通过耦合PROSPECT 叶片辐射传输模型［18］和SAILH 冠层结构模型［19］得到的整体模型。PROSPECT 模型输入参数主要包括叶片结构参数、叶绿素含量、干物质含量和等效水厚度，其中结构参数可为一个假设参数，本文根据实测数据拟合取1.31。SAILH 模型输入参数包括叶片光谱信息、叶面积指数、平均叶倾角、热点参数、土壤亮度参数、漫反射系数、观测天顶角、太阳天顶角、观测相对方位角。其中叶片光谱信息(反射率、透射率)采用PROSPECT 模型模拟的输出结果，其他参数可根据光谱获取时的实际观测信息确定，则影响冠层光谱的变动参数为叶绿素含量、干物质含量、等效水厚度、叶面积指数。

PROSAIL 模型敏感性分析是为了分析评价各参数对模型的影响程度，从而确定出模型参数影响的光谱波段的敏感范围，它是利用PROSAIL 模型初步反演水稻叶绿素含量的基础。本研究采用一种改进Sobol 全局敏感性分析方法［20］分析PROSAIL 模型中叶绿素含量、等效水厚度、干物质含量参数变化以及参数之间相互作用对模拟水稻冠层光谱信息的影响。该方法是一种基于方差的全局敏感性分析算法，设非线性模型输入参数为xi，则模型总体方差为

式中 Vi——参数xi变化单独引起的方差

Vij——参数xi、xj间相互作用的方差

Vij…k——参数xi、xj、…、xk相互作用的方差

则参数xi的一、二阶敏感度及总敏感度为

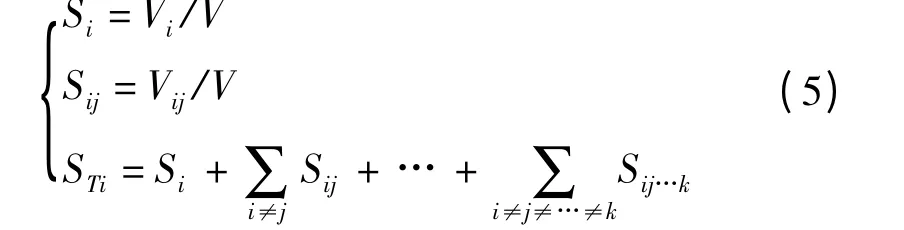
式中 Si——xi的一阶敏感度

Sij——xi的二阶敏感度

Sij…k——xi的多阶敏感度

STi——xi的总敏感度

采用蒙特卡罗方法估计可得到参数的总敏感度。在计算过程中，对STi进行归一化处理，进而评价模型中各参数的总敏感度。

1.4 混合建模方法

1.4.1 模型结构

基于PROSAIL 模型和LSSVM 软测量模型各自的优势，提出将两种模型相结合的混合建模方法，以实现对水稻叶绿素含量的精准估测，提高模型的普适性。水稻叶绿素含量整体估测流程如图1 所示。

混合建模方法首先利用PROSAIL 辐射传输机理模型模拟冠层光谱，建立查找表，并将采集的冠层光谱反射率与查找表中模拟冠层光谱反射率比较，通过代价函数确定最优解，初步反演水稻叶绿素含量，然后采用LSSVM 建立误差模型，弥补PROSAIL模型产生的偏差，最终由机理模型与LSSVM 误差模型相结合对水稻叶绿素含量进行估测。该模型的预测输出C 为

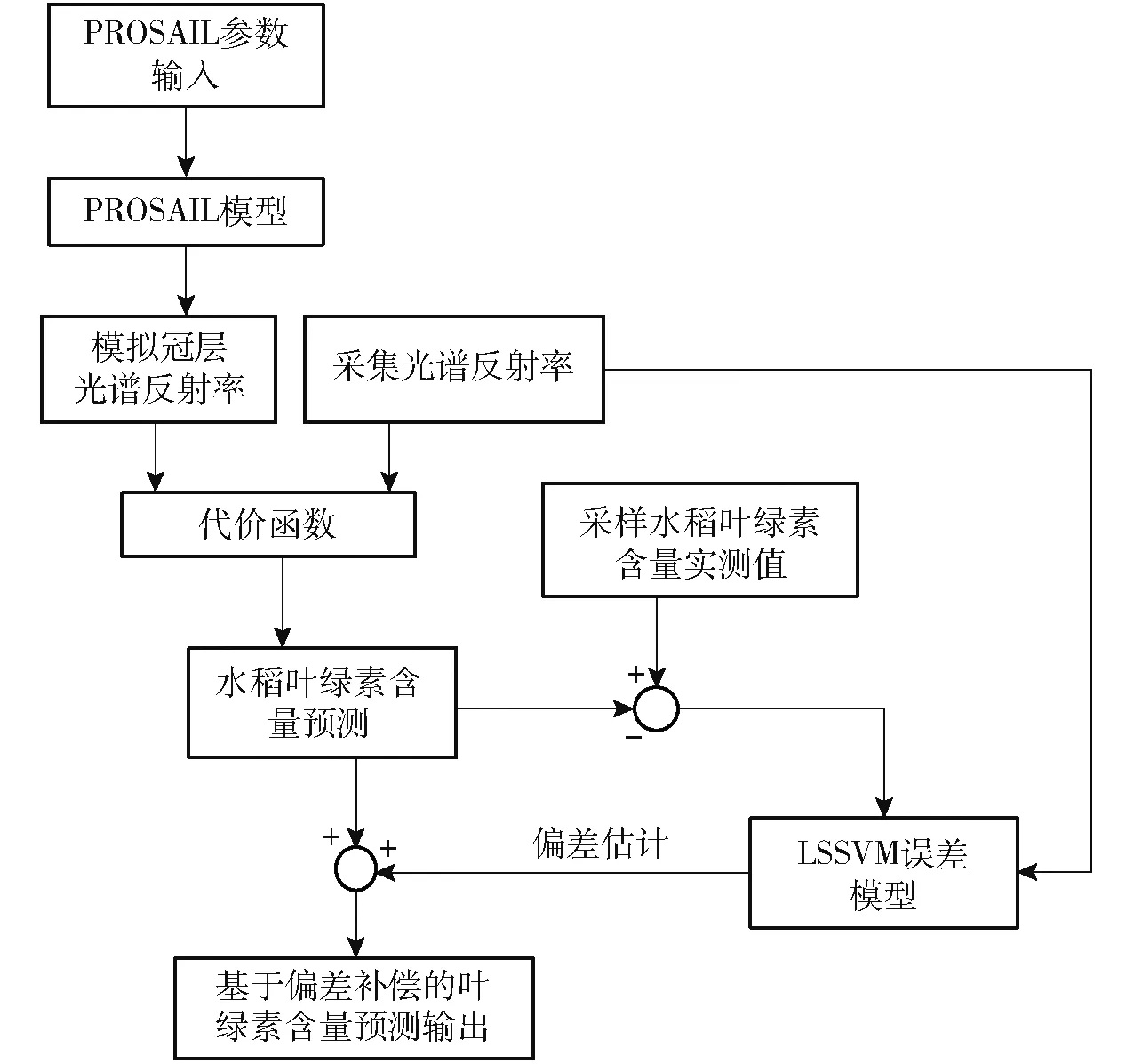
图1 基于混合模型的水稻叶绿素含量估测流程图Fig.1 Flow chart of rice chlorophyll content estimation based on hybrid model

式中 C——基于PROSAIL 模型的叶绿素含量预测值

输出C 的目的是进一步提高叶绿素含量估测精度。

1.4.2 回归LSSVM 误差模型

LSSVM 算法是由SUYKENS 等［21］提出的一种改进SVM 算法。该算法将SVM 的求解从二次规划问题转化为线性方程组，降低了运算的复杂度，提高了求解效率，可以很好地用于函数回归问题。

本文采用LSSVM 算法构建误差模型，选取{xi，ei}为样本集，其中xi=(X，C)，X 为PROSAIL 模型输入光谱变量，ei=CActual-C，其中CActual为水稻叶绿素实测值，i=1，2，…，L，L 为样本数。

LSSVM 的优化问题描述为

式中 w——权值向量 ζi——误差

γ——正则化参数

b——偏差 φ——特征映射

J——LSSVM 的目标函数

〈·〉——内积运算

为求解优化问题，引入Lagrange 函数

式中 αi——拉格朗日乘子

α——拉格朗月乘子向量

令式(8)偏导数为0，消去w 和ζi，则

其中

式中 e——偏差矩阵 Ω——核矩阵

Z——n 维单位矩阵求解上述矩阵可得到相应α 和b 的值，从而得到水稻叶绿素含量误差估计函数为

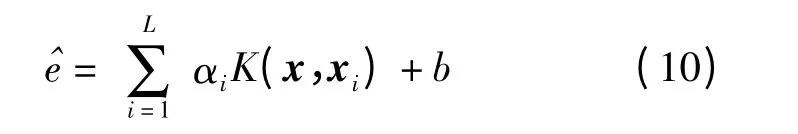
其中

式中 σ——核函数参数

1.5 统计分析

在模型性能评价方面，本文选取决定系数R2和均方根误差RMSE (单位:mg/dm2)作为模型拟合度和反演精度的评价指标，衡量拟合模型的效果［22］。其中R2越接近1，表明预测值与实测值之间的相关性越高;R2越接近0，表明预测值与实测值之间的相关程度越弱。RMSE 越小，表明模型精度越高。

2 结果与分析

2.1 模型敏感性分析与查找表建立

本文主要分析PROSAIL 模型中叶绿素参数的变化对水稻冠层光谱信息的影响。PROSAIL 模型输入参数设置如表1 所示。

表1 PROSAIL 模型输入参数设置Tab.1 PROSAIL model input parameters setting

采用改进Sobol 方法对PROSAIL 模型进行全局敏感性分析(图2)发现，叶绿素含量主要影响430 ～760 nm 波段的冠层反射率，而对900 nm 以上波长的冠层反射率影响很小。在900 nm 以下波段，水分含量的变化对冠层光谱信息影响不大，光谱反射率的影响主要集中在950 nm 以上波长。叶面积指数和干物质含量的变化在400 ～1 000 nm 光谱范围内均存在敏感性，且700 nm 以上波长对干物质含量敏感性显著增加。

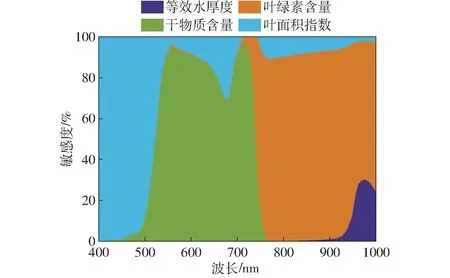
图2 PROSAIL 模型各参数敏感度分析Fig.2 Total sensitivity analysis of PROSAIL parameters

根据参数敏感性分析结果得到各参数的敏感波段，可用于构建水稻叶绿素含量的估测模型。根据光谱采集过程的实际情况，得到查找表的各输入参数及变化范围如表2 所示。

将各参数的不同组合代入PROSAIL 模型进行冠层反射率模拟，建立水稻叶绿素含量的查找表，并在敏感波段范围内，将实测冠层光谱反射率与查找表中反射率比较，采用文献［23］中最小二乘法构建代价函数，初步反演叶绿素含量。

表2 PROSAIL 模型查找表输入参数范围Tab.2 Input parameters range in PROSAIL modelfor lookup table

2.2 不同光谱指数的叶绿素含量相关性与模型构建

将光谱反射率转换为不同植被指数，并选取与叶绿素关系较为紧密的13 种植被指数［8］。为了检测本文方法的性能，首先分别采用各植被指数进行线性、指数、乘幂和对数等统计模型的模拟，建立基于植被指数的单因子预测模型(Single factor estimation model，SFEM)，不同光谱指数与水稻叶绿素含量的相关性如表3 所示。

表3 基于植被指数的水稻叶绿素含量最佳估测模型R2Tab.3 R2 of optimal estimation models based on vegetation index for chlorophyll content in rice

由表3 可以看出，基于光谱指数GNDVI、RSI 和(SDr- SDb)/(SDr+ SDb)的乘幂关系统计模型及MCARI 指数关系统计模型与水稻叶绿素含量相关性较高，决定系数分别为0.625 6、0.620 3、0.647 1和0.631 9，模 型 分 别 记 为SFEMGNDVI、SFEMRSI、SFEMSDr-SDb、SFEMMCARI。另外，本文结合这4 种植被指数作为多因子输入，水稻叶绿素含量为输出，构建多因子预测模型(Multi-factor estimation model，MFEM)，包括构建LSSVM 误差模型，补偿PROSAIL模型输出与实测值之间的偏差，混合模型标记为MFEMPROSAIL-LSSVM。同时单独采用PROSAIL 模型建立查找表反演叶绿素，标记为MFEMPROSAIL。为进一步比较模型之间性能，还分别采用PLS、LSSVM 和BP 神经网络建立基于植被指数组合的多因子预测模型，模型分别记为MFEMPLS、MFEMLSSVM、MFEMBP。其中，LSSVM 模型中惩罚因子γ 与核函数参数σ 采用具有全局搜索性能的改进粒子群算法［34］进行寻优。BP 神经网络模型采用3 层结构，网络模型对不同隐含层结点数进行训练以确定最佳隐含层结点数m，迭代次数为1 500，学习目标为0.001，学习率为0.01。利用采集的几个关键生育期共400 组训练样本数据对模型进行训练，得到最优模型如表4 所示。

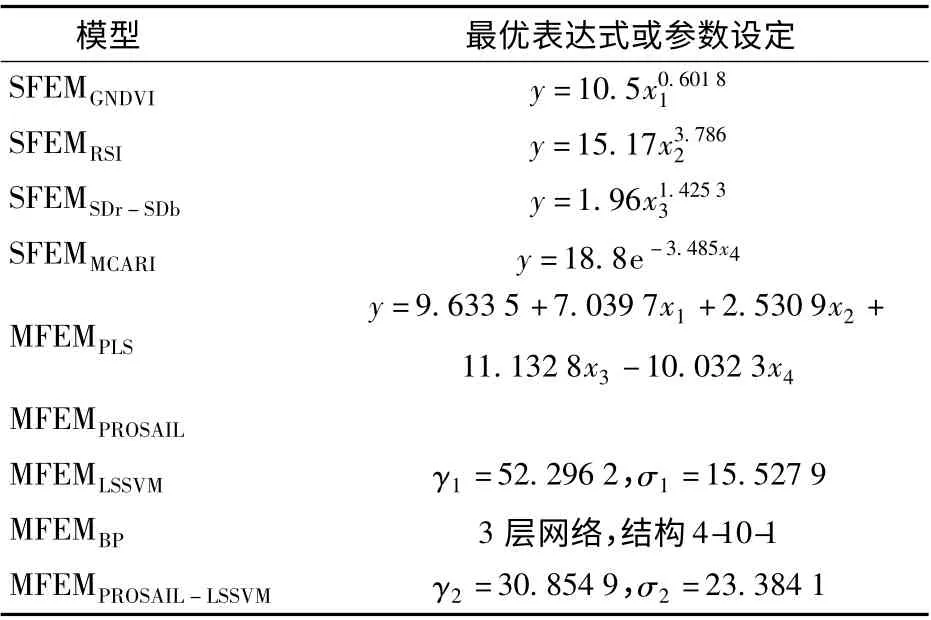
表4 水稻叶绿素含量最优估测模型Tab.4 Each optimal estimation model for chlorophyllcontent in rice

2.3 模型检验分析

在采集到的检验样本中，随机抽取115 个检验样本，采用表4 建立的最佳模型对样本数据进行验证，相应的预测模型建模精度和检验精度如表5 所示，各模型对水稻叶绿素估测值和实测值的散点图如图3 所示。

表5 预测模型的建模及检验精度Tab.5 Calibration and validation result of estimation model

由图3 可以看出，不同单因子预测模型所得的预测值分布状态较为相近，不存在较大的区别，其中SFEMSDr-SDb分布相对紧密一些。虽然单因子预测模型具有一定预测精度，但沿直线y=x 分布较为分散，表明估测值与实测值之间存在一定偏差。

图3 不同模型的叶绿素含量实测值与估测值比较Fig.3 Comparison of measured and estimated values of chlorophyll content for different models

结合4 种植被指数为输入的多因子预测模型MFEMPLS、MFEMLSSVM、MFEMPROSAIL-LSSVM、MFEMBP对水稻叶绿素含量的估测，与单因子最优预测模型SFEMGNDVI、SFEMRSI、SFEMSDr-SDb、SFEMMCARI相比，分布更为紧密，尤其是本文提出的MFEMPROSAIL-LSSVM模型，其预测结果沿直线y =x 的分布状态较优，相比单因子预测模型，有更少的预测值偏离直线y =x，同时也在不同程度上优于MFEMPLS、MFEMLSSVM、MFEMBP模型，显示了优异的预测效果，能够有效减小不同生育期的差异对该模型的影响。

从表5 可以看出，基于多因子输入的预测模型整体上要比单因子预测模型具有更小的RMSE，由于单因子预测模型使用光谱信息有限，一些干扰无法有效排除，因而误差往往较大。而多因子预测模型同时使用了多个光谱指数作为自变量，更大程度利用有效信息，因此可以提高模型精度。同时多因子预测模型可减少因同谱异物及同物异谱等原因形成 的 偏 差。 可 以 看 出， 本 文 提 出 的MFEMPROSAIL-LSSVM多因子预测模型无论对于建模集还是检验集，都得到了最小的RMSE 指标。另外，对于建模集，MFEMPROSAIL-LSSVM模型和基于LSSVM 的多因子预测模型具有较高的决定系数，分别为0.740 6 和0.739 3，高于其他预测模型。对比MFEMLSSVM模型，虽然本文建立的模型在决定系数指标方面没有较大优势，但在检验集中，MFEMPROSAIL-LSSVM模型提供了最高的决定系数，不仅高于单因子预测模型，也在一定程度上优于其他多因子预测模型，表明提出的方法其估测值与实测值之间具有更好的相关性。表6 列出了不同模型估测叶绿素的统计特征。

表6 不同模型估测水稻叶绿素含量的统计特征Tab.6 Statistical characteristics of different models in estimating chlorophyll content in rice μg/cm2

由表6 可以看出，SFEMRSI模型对水稻叶绿素估测的平均值低于实测平均值，SFEMMCARI和SFEMGNDVI模型估测的平均值高于实测平均值，且SFEMGNDVI模型的估测值分布较为集中，SFEMMCARI模型的估测值分布较为分散，对于较大值和较小值分别有过高估测和过低估测的倾向，而MFEMPROSAIL-LSSVM、MFEMLSSVM、MFEMBP模型对叶绿素的估测值与实测值较为接近，尤其MFEMPROSAIL-LSSVM和MFEMLSSVM多因子预测模型估测叶绿素最大、最小值、均值和标准差都比较接近实测值。

3 讨论

在东北水稻叶绿素含量估测方面，本文选择相关性较高光谱指数GNDVI、RSI、(SDr-SDb)/(SDr+SDb)和MCARI 作为水稻几个关键生育期叶绿素动态变化的输入因子，并分别构建基于植被指数的单因子预测模型及多因子预测模型，都在一定程度上获得了较为满意的精度。相对利用全部光谱信息建模，基于光谱指数建立的模型较为简单，尽管仅使用了几个光谱波段，但数据利用率较高，精度也较高。通过特征波段组成光谱指数，可剔除不相关变量，进而得到性能较好的估测模型。

通过本文仿真对比研究发现，在建立的多个模型中，多因子预测模型整体上优于单因子预测模型，可能因为单因子预测模型建立时，参与建模的光谱信息过少而导致模型稳定性不够，且容易受到背景信息的干扰而降低模型精度。水稻等作物叶绿素含量的差异体现在光谱的多个波段上，而其他波段构建的光谱指数对叶绿素的影响往往不可忽视。因此，文中多因子预测模型具有较好的估测效果。另外，在多因子预测模型中，基于PROSAIL 模型偏差补偿的混合模型，其预测值与实测值之间具有更好的拟合性(R2=0.740 6，RMSE 为0.985 2 mg/dm2)。可见，在相同波段或植被指数输入条件时，对模型偏差有效补偿可进一步提升模型估测性能。

在对水稻叶绿素含量预测时，采用一年或两年数据构建水稻叶绿素含量预测模型往往存在一定不足，但本文可为下一步开展长时间序列的基于高光谱数据的水稻叶绿素含量估测奠定基础。此外，水稻等作物叶绿素含量估测目前还没有统一的标准模型，虽然本文构建了水稻在4 个关键生育期内的整体动态混合模型，但最佳的叶绿素预测模型也会因生育期、品种、长势等不同而受影响。由于受到天气、技术、设备等多方面影响，未能获取更多生育期(如孕穗期、开花期、灌浆早期、灌浆末期)的数据信息，本文所得的最优模型在一定程度上也会受限于本次测量结果。因此，在多个不同水稻品种、不同关键生育期及不同年份水稻样本上继续测试，积累更多的试验数据，进而将本研究更好地应用于水稻全生育期及其它品种以进一步提升预测模型的稳定性及普适性，是今后需着重探讨研究的一个问题。

4 结束语

利用PROSAIL 辐射传输机理模型结合LSSVM误差模型，筛选出4 种与叶绿素相关性较高的植被指数GNDVI、MCARI、RSI 和(SDr-SDb)/(SDr+SDb)作为输入，建立4 个关键生育期内的整体多因子预测混合模型，用来估测水稻叶绿素含量，并与其他预测模型进行了比较。结果表明，相比单因子输入的预测模型，本文建立的MFEMPROSAIL-LSSVM模型具有较低的估测误差和较高的估测精度;与MFEMPROSAIL模型及其他多因子预测模型MFEMPLS、MFEMLSSVM、MFEMBP相比，MFEMPROSAIL-LSSVM模型具有更高的估测精度和良好的鲁棒性。另外，与单纯数据驱动模型相比，本文方法不仅具有较高估测精度，而且具有更为严格的理论基础和较明确的物理意义。本文建模方法可为利用高光谱信息反演水稻叶绿素含量提供新的研究思路，为水稻叶绿素含量的动态监测提供了模型依据。