基于可压缩模型的排气歧管流场分析
2020-07-07李泽宇
李泽宇
中国第一汽车股份有限公司天津技术开发分公司,天津300462)
0 引言
目前,为应对排放和油耗法规日益严格的要求,汽油机正向小排量、涡轮化的方向发展。排气歧管是发动机排气系统的重要部件之一,设计中应关注其内部流场状态,重点关注氧传感器位置的合理性、催化器载体入口速度均匀性以及整体压降性能,前两者影响排放性能,而排气压降则与油耗性能密切相关[1]。
CFD(Computational Fluid Dynamics,计算流体动力学),原理是将现实中连续的流体域离散化后通过数值计算的方法求解流动的微分方程。相比试验方法,成本更低,周期更短。采用CFD方法可以在前期高效地指导排气歧管零部件的流场设计,但为了保证其计算结果准确性,需要选择正确的计算模型和方法,本文作者讨论了流体可压缩性模型对于排气歧管流场的计算准确性影响,并对指导设计的判断依据进行了探讨。
1 计算模型
计算模型为图1所示的某2.0T发动机的集成式排气歧管。目前先进的发动机采用集成式排气歧管的设计,可以更有效地利用排气能量进行涡轮增压并能提高暖机速度[2]。计算模型包括各气缸排气口、两个氧传感器、TWC(三元催化器)和GPF(颗粒捕捉器),模型保留了涡轮增压的流道,但不对内部的涡轮扇叶进行计算。计算模型通过抽取几何数据气流流动的内表面获得。文中算例采用成熟的商业CFD软件STAR-CCM+进行流动求解,STAR-CCM+同时还具备强大的前处理和网格生成、检查功能,对于质量较好不需要进行几何清理的排气歧管模型,完全可以使用该软件完成从前处理、计算求解到后处理的全部工作。

图1 排气歧管模型
2 CFD计算流程
2.1 网格生成
利用STAR-CCM+软件强大的网格处理功能,将数据导入后即可生成三角形的面网格。检查面网格符合软件计算要求后,采用多面体网格方案对计算的流体域进行离散,经验证网格大小设置为2 mm可以比较准确地反映几何特征,并在此基础上生成2层共0.8 mm厚的边界层网格,以提高近壁面流场计算的准确性,入口和出口设置拉伸网格以稳定流动,提高计算收敛性。TWC和GPF部分单独处理为Trim网格,网格大小同样为2 mm,与主流区域保持一致。最终体网格数量为150万左右,符合工程计算能力的同时,也能保证计算精度。
2.2 求解模型
根据排气歧管内部流场的关注内容,采用稳态计算方法可以定量地评价其性能,湍流模型采用适用范围较广的Realizableκ-Epsilon模型,使用二阶求解精度进行计算[3]。
在流体力学中,一般认为马赫数Ma>0.3时需要考虑流体的可压缩性[4]。排气歧管中排气温度较高且存在变化,粗略估计其Ma一般在0.3左右,分别采用可压缩模型和不可压缩模型计算验证其对于结果的影响,采用不可压缩模型时使用分离隐式求解器计算,而采用可压缩模型时使用耦合隐式求解器获得更稳定的收敛。
2.3 边界条件
分别计算4个工况,对应1~4缸各排气口分别打开、其他排气口关闭的状态。采用质量流量定义入口,计算全功率点的工况,流量定为730 kg/h,排气温度1 123 K,不可压缩模型中气体密度根据排气温度定为0.315 kg/m3,动力黏度4.55×10-5Pa·s;可压缩模型中排气密度随计算温度变化,动力黏度根据萨特兰定律确定。对于TWC和GPF,采用多孔介质进行模拟,根据试验测定结果设置其惯性阻力系数和黏性阻力系数。
2.4 收敛准则
计算的收敛性判断通常根据残差值确定,一般要求小于10-3,但STAR-CCM+软件的残差统计特点导致某些残差值经常不能降低到该水平。因此一般认为计算的最后500步中,如果监测的物理量都收敛到了计算需求的精度,且残差已经稳定,则认为计算已经收敛。在该案例中,不论是可压缩计算方法还是不可压缩计算方法,在5 000步时计算都已经收敛。
3 计算结果
3.1 排气歧管内流场基本参数对比
管路内流场计算一般都会关注整体压降以及管路内部的速度分布,可以表示计算结果的总体特征,并验证计算的合理性。
3.1.1 压降计算结果对比
压降是排气歧管设计中的一项重要指标,因为排气歧管的压降损失是排气损失的重要组成部分,进而对发动机热效率和油耗性能产生影响。在实际计算中压降通常也作为判断是否达到收敛要求的依据。可压缩模型与不可压缩模型的整体压降对比如表1所示。
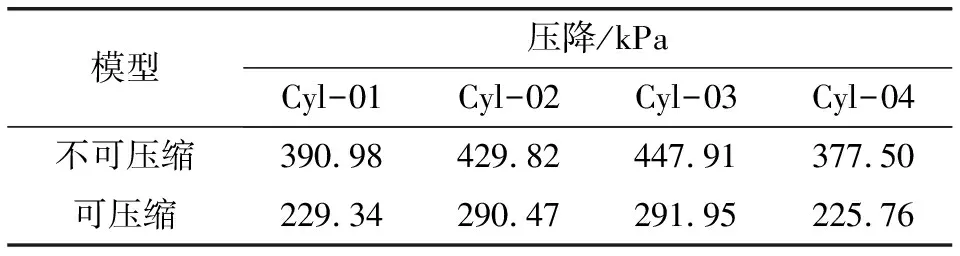
表1 计算结果-压降对比
从表1可以看出:采用可压缩方法进行计算时,整体压降相对于不可压缩方法都显著下降,但各工况的相对偏差趋势一致。造成这种现象的原因将在下一小节讨论。
3.1.2 流场密度对比
可压缩计算模型最重要的特点是采用了理想气体模型并加入能量方程,使得密度随计算进行求解,对于预测Ma大于0.3的流动更加准确。以气缸1排气工况为例,图2显示了流场内部截面上的密度变化,可以看出流场出口处密度趋于0.32 kg/m3左右,与不可压缩模型的计算设置较为接近,但在涡轮通道的位置,密度变化的范围很大。图3则是可压缩模型的Ma分布云图,出口处的Ma已经超过0.3,而涡轮通道内Ma更高。综上所述,当计算带有涡轮通道的集成式排气歧管时,采用可压缩算法是十分必要的。
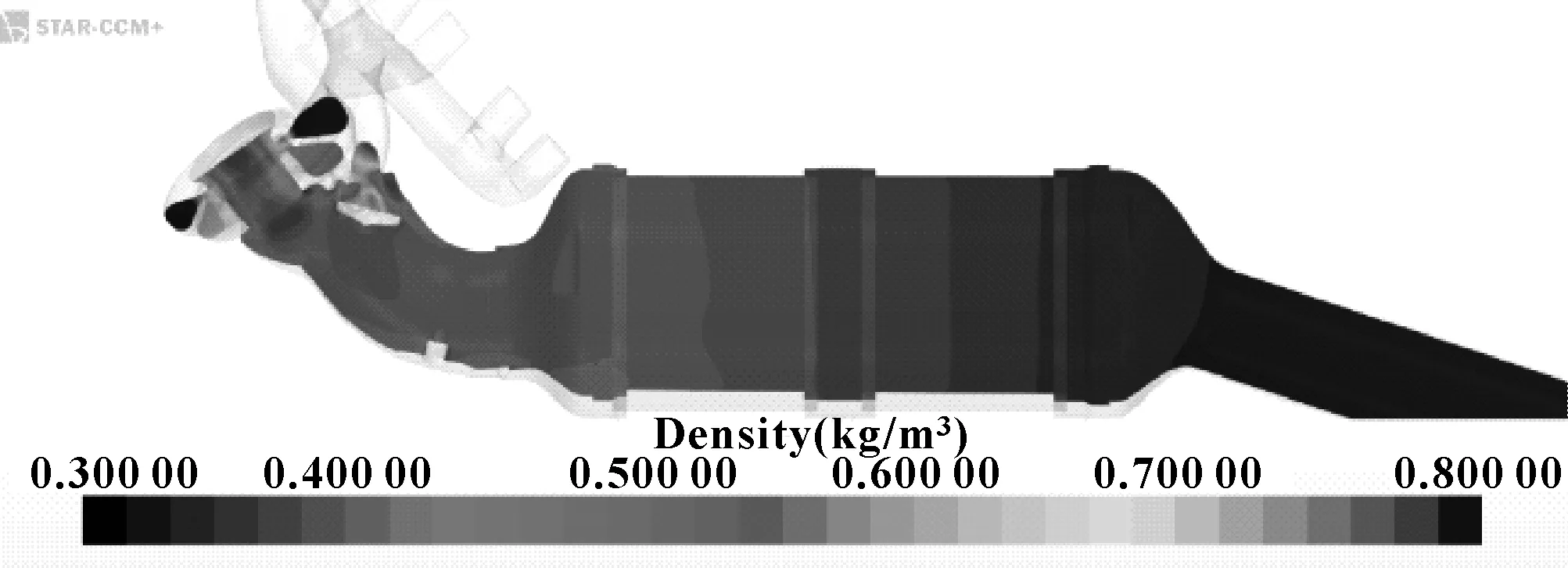
图2 可压缩计算模型内部密度云图

图3 可压缩计算模型内部Ma云图
3.1.3 流场速度对比
速度是流场的重要标量之一,可以反映模型计算结果的特点。仍然以气缸1排气工况为例,通过如图4所示的截面速度对比可以看出,速度分布最明显的差异也集中在涡轮通道部分,同时也会影响到下游的多孔介质区域,对出口附近流场影响不大。
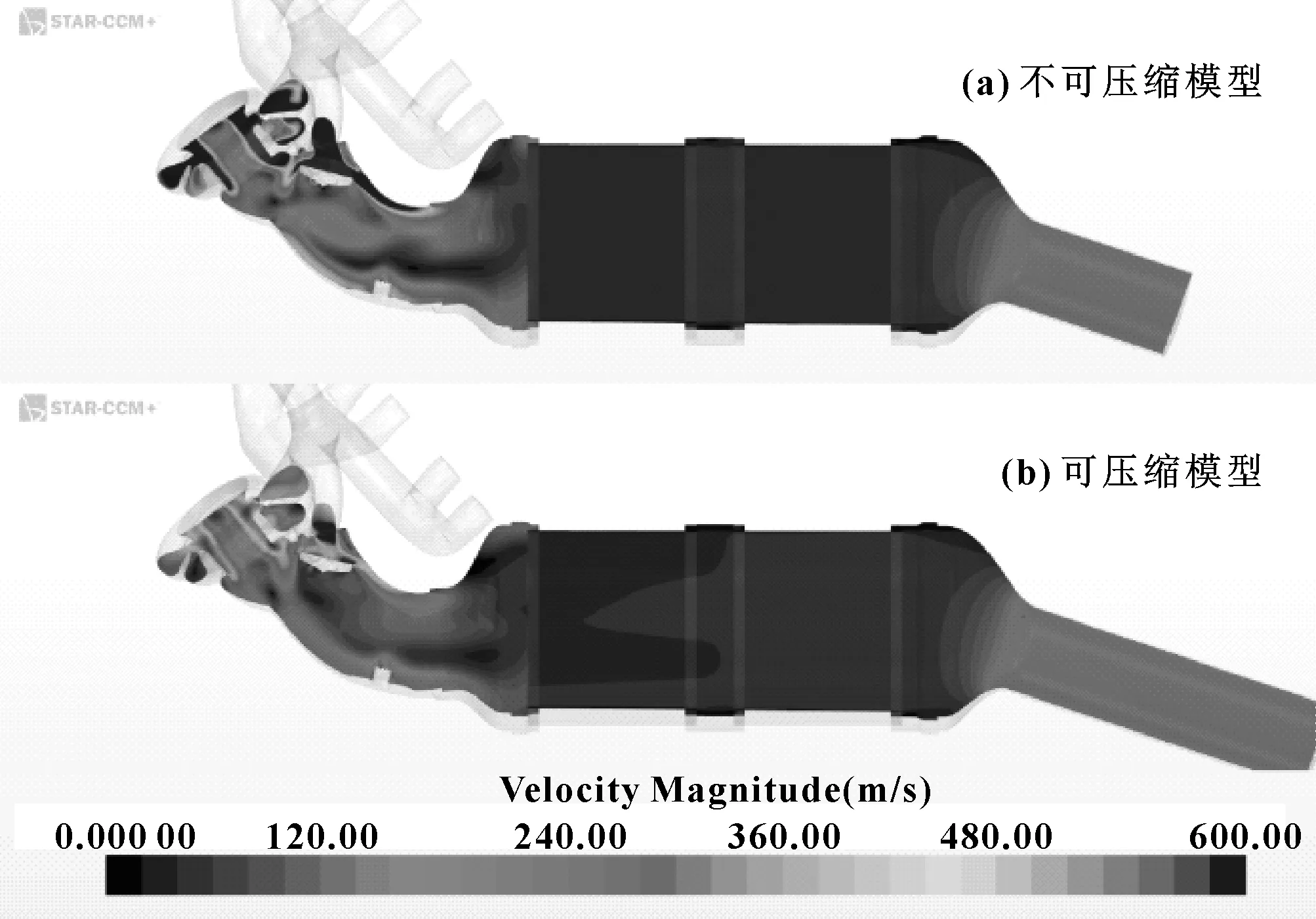
图4 流场内部截面速度分布对比
3.2 排气歧管设计性能指标对比
排气歧管设计时需要考虑氧传感器位置合理性以及催化器载体入口的均匀性,一般采取定量与定性结合的方法进行分析。
3.2.1 氧传感器位置合理性分析
氧传感器位置的合理性主要通过其表面最大速度判断,有学者采用氧传感器表面速度大于100 m/s即为合格的标准[5],文中则采用速度比vratio=vsensor/vsurface作为标准,其中,vsensor为氧传感器表面最大速度,vsurface为氧传感器附近截面平均速度。采用这样的标准是因为排量较大时,速度绝对值并不能真实体现氧传感器位置合理性。图5和图6分别是氧传感器1、2表面与其所在截面的速度云图。

图5 氧传感器1及所在截面速度云图
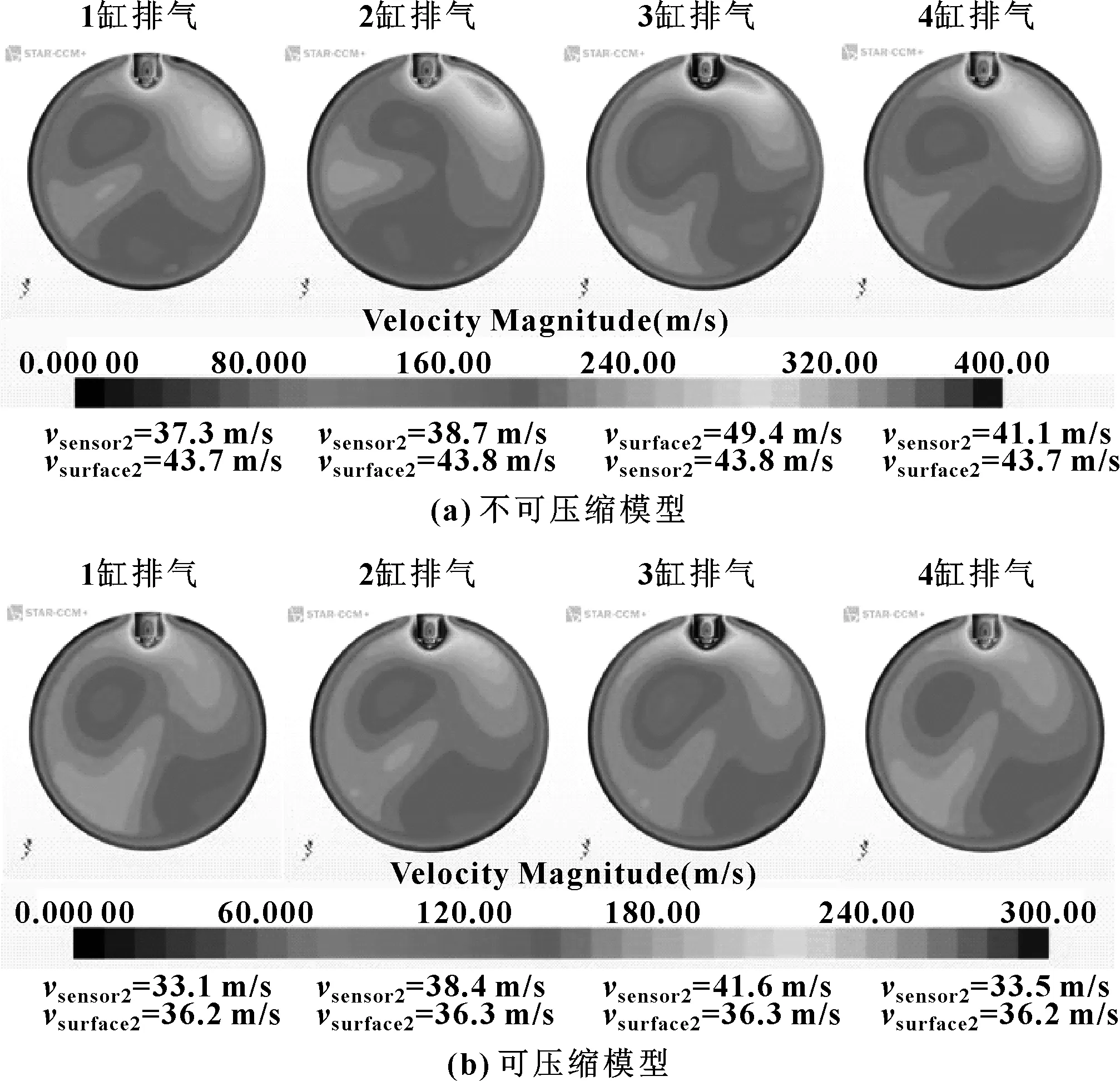
图6 氧传感器2及所在截面速度云图
对比速度云图可以看出,模型可压缩性对计算的影响主要体现在氧传感器1部分。这是因为氧传感器1更加靠近涡轮通道,气流速度快,受影响更大,氧传感器2位于TWC之后,气流经过后速度变慢,流场也更加均匀。表2和表3分别是氧传感器1和2的速度比率,可以看出对于氧传感器1,可压缩模型的计算结果相对偏小,达标风险大,而对于氧传感器2,速度比率结果反而相对偏大。如果氧传感器1采用氧传感器表面速度大于100 m/s的判定标准,可以轻易达标,但经计算发现可压缩模型下气缸1、3、4的速度比率都不足0.8,说明排气歧管设计尚有优化空间,氧传感器2在两种计算模型下都能比较轻易地达标。因此设计中应重点考虑位于流场速度较快、稳定性较差区域的氧传感器布置位置。
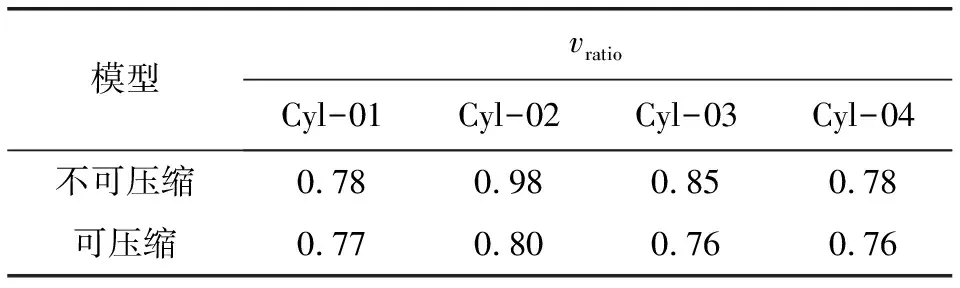
表2 氧传感器1速度比率

表3 氧传感器2速度比率
3.2.2 催化器载体入口速度均匀性分析
催化器入口的速度均匀性对于提升催化器的反应效率和耐用性都有很大影响。可定义催化器入口速度分布均匀性系数UI=1-ΣAi|ui-uaverage|/2ΣAiui, 其中:ui是各单元点速度,uaverage是入口平均速度,Ai是催化器入口速度分布的面积。表4和表5分别是TWC和GPF的入口速度均匀性系数计算结果。

表4 TWC载体入口UI计算结果
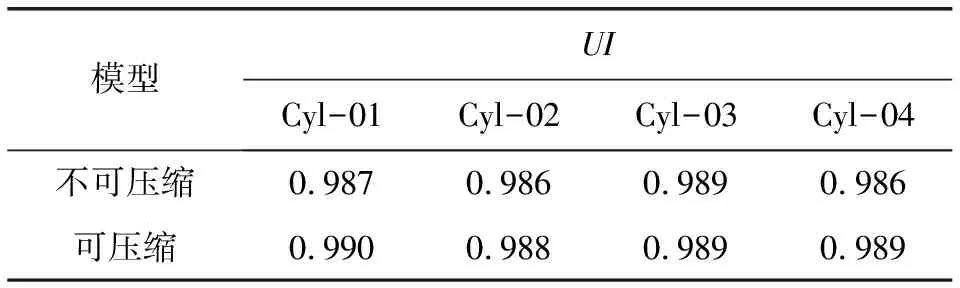
表5 GPF载体入口UI计算结果
图7和图8分别是TWC和GPF入口速度云图,靠近涡轮通道的TWC入口速度分布差异明显。采用可压缩模型计算时速度均匀性更易达标,这可能主要是因为可压缩模型的整体流速较小,流场更均匀。而位于TWC之后的GPF入口,因经过催化器后流速较慢,两种计算方法的分布特点类似,计算结果也较为相似。
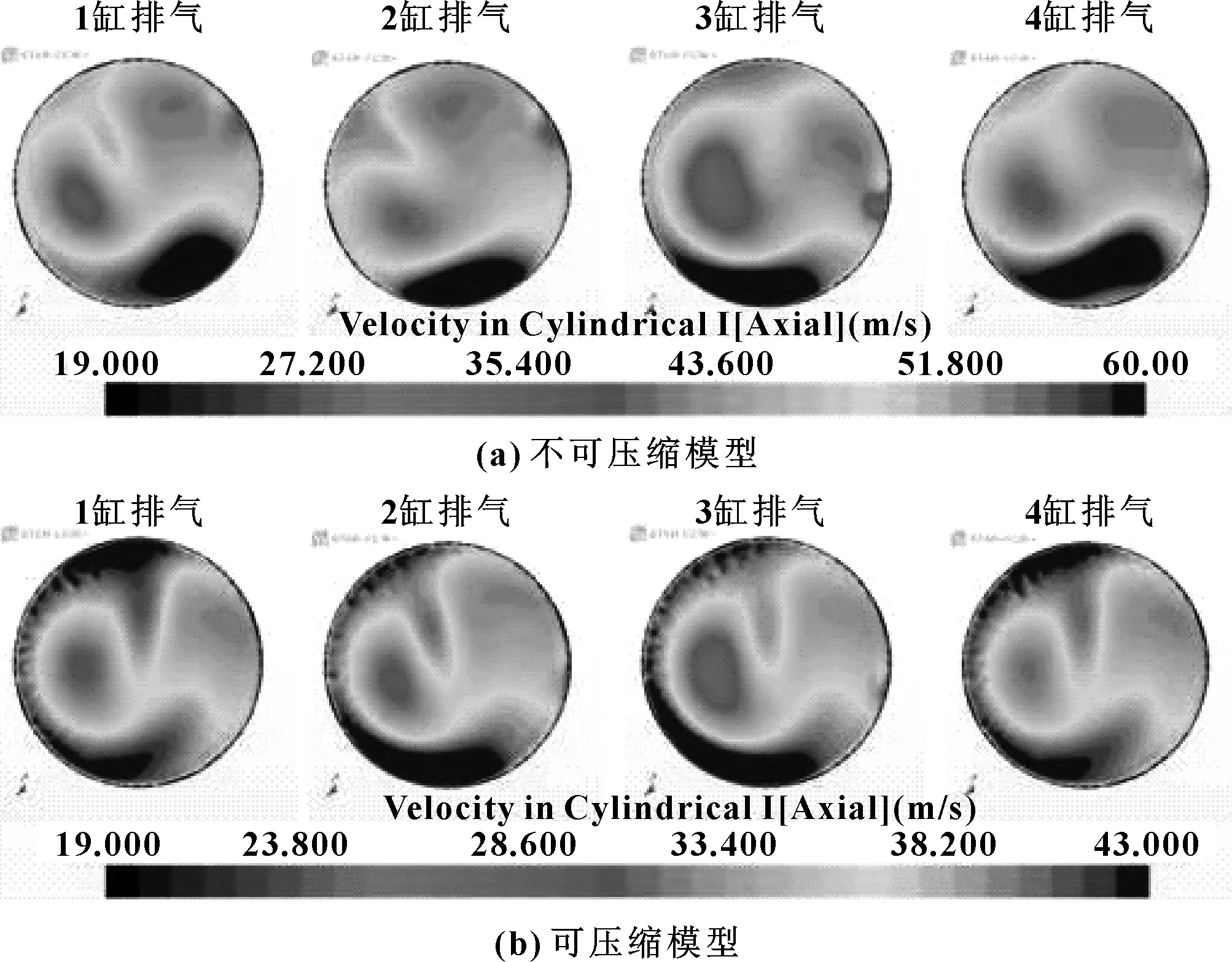
图7 TWC入口速度云图

图8 GPF入口速度云图
4 结论
通过对带涡轮增压通道的排气歧管计算,讨论了可压缩模型对于计算结果的影响,结论如下:
(1)具有涡轮结构的集成式排气歧管局部流速很快,体现较强的可压缩性,不可压缩模型对局部密度估计过小,造成速度偏大,压损也相应偏大很多,流场分布差异明显,应采用可压缩模型进行计算;
(2)可压缩模型会使氧传感器评价指标变差,且对于大排量的排气歧管考虑氧传感器表面最大速度与当地速度之比,比单独考虑氧传感器表面最大速度更为合理;
(3)可压缩模型对于催化器入口速度均匀性的计算结果要好于不可压缩模型,且对于紧耦合布置的第二级催化器或颗粒捕捉器,可压缩模型对计算结果的影响较小。
