三角网格模型骨架提取算法
2020-07-06王洪申张家振张小鹏
王洪申 张家振 张小鹏

摘 要:骨架图能够直观表达三维模型几何形状,很好地反映模型的拓扑特征,在工业机器人抓取、特征识别等领域有着广泛的应用。针对三角网格表达的工业零件给出一种骨架提取算法,该算法采用Reeb图对三角网格进行骨架的抽取运算。首先读取三角网格文件,并对复杂的三角网格进行简化处理,然后遍历所有的三角网格,采用Dijkstra算法抽取基本点集,根据定义的连续函数计算每个顶点的函数值,最后根据函数值得出模型的基本骨架。实验表明,该算法具有良好的计算效果和效率,提取出的骨架图较好地保存了三维模型拓扑结构和姿态,可作为后续研究三维模型搜索的特征描述符。
关键词:骨架图;三角网格;三维模型;拓扑结构;Reeb图
中图分类号:G633.6 文献标识码:A
文章编号:1003—6199(2020)02—0145—05
Abstract:The skeleton diagram can visually express the geometry of the 3D model and reflect the topological features of the model well. It has a wide range of applications in the fields of industrial robot capture and feature recognition. A skeleton extraction algorithm is proposed for the industrial parts expressed by the triangle mesh. The algorithm uses the Reeb diagram to extract the skeleton from the triangular mesh. First read the triangle mesh file,and simplify the complex triangle mesh,then traverse all the triangle meshes,extract the basic point set by Dijkstra algorithm,calculate the function value of each vertex according to the defined continuous function,and finally The function deserves the basic skeleton of the model. Experiments show that the proposed algorithm has good computational efficiency and efficiency. The extracted skeleton map preserves the topology and pose of the 3D model,and can be used as a feature descriptor for the subsequent research of 3D model search.
Key words:skeleton diagram;triangular mesh;3D model;topology;Reeb diagram
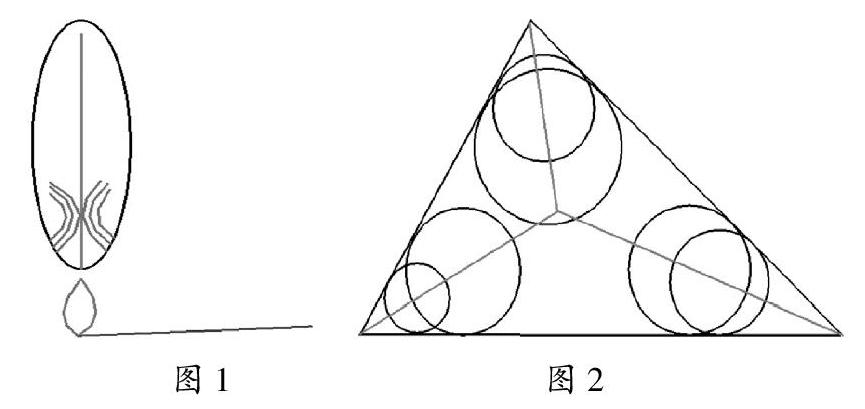
随着计算机图形学的发展,对三维模型的研究日益深入,骨架作为形状表示的一种有效形式,在三维模型的各个研究领域被运用。骨架的狭义定义最初由Blum[1]提出,当时他称骨架为“中轴”(Medial Axis)[2]。骨架的经典定义有两种[3]:一种是烧草模型,如图1所示,从模型表面开始点火,火焰从物体边界上的两点同时向内部推进,轨迹随时间形成等距的同心圆,同心圆的相遇点所构成的集合即为骨架;另外一种是更直观的定义,即最大圆盘模型。如图2所示,骨架点是所有最大圆盘的圆心集合,最大圆盘即是完全包含在物体内部且至少与物体边界相切于两点的圆。骨架上的每一个点都是这些内切圆的圆心,这些圆沿着骨架分布正好填充物体的内部。由于模型的骨架很好地保留了模型的拓扑形态及其连接特性,所以经常被用于模型渲染、模型表面重建、碰撞检测、模型检索等应用中,在工业零件的视觉识别领域也有广泛的用途。
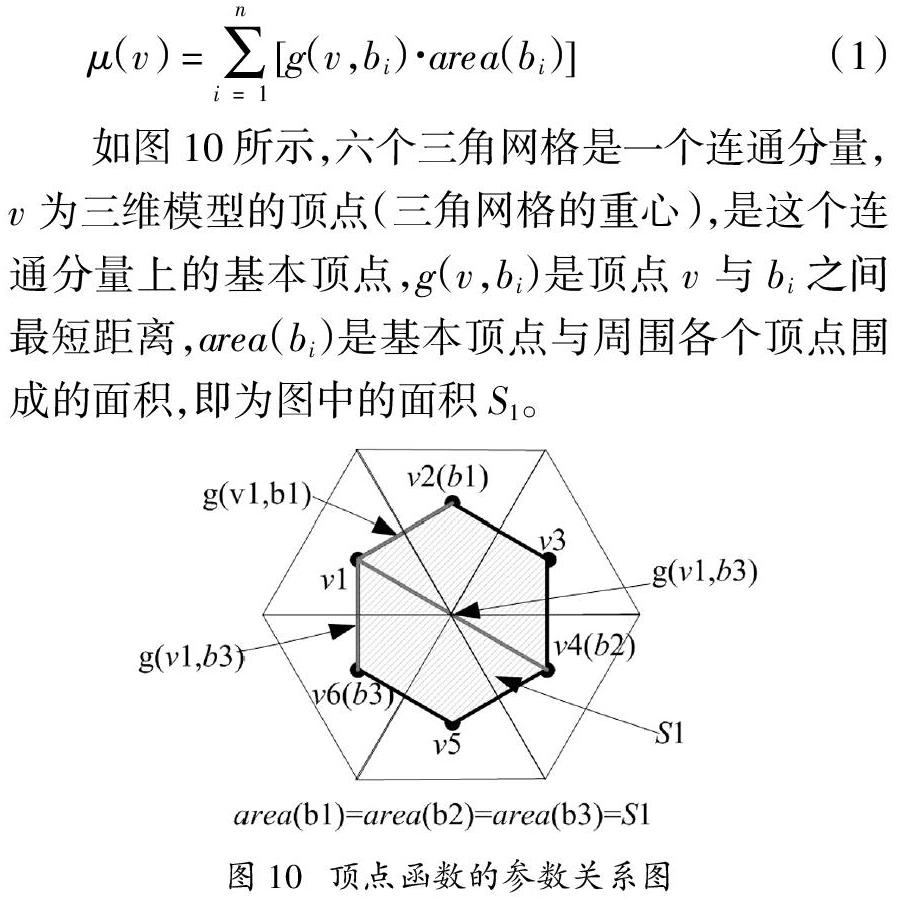
针对三维模型,骨架的提取方法主要有如下几种:(1)基于拓扑细化技术[3]。该类算法主要用于体表示的模型上,通过不断地进行体元素的削减来实现骨架的抽取,所以整个过程比较耗时,效率不高;(2)基于距離矩阵的方法[4]。它一般也是针对体表示的模型,通过计算每个体元素的距离来求取模型的脊点;(3)基于二维图像领域的Voronoi图技术。有学者将二维领域的Voronoi图技术引入到三维模型的骨架提取中来,Dey等人提出过一种利用Voronoi图直接近似中轴的算法[2];(4)烧草模型法。正如上面的烧草模型所述,在模型的一端点火,模型两侧同时燃烧,火焰相聚处形成连贯的烧痕,这就是模型骨架的相似轨迹,但是这种方法理论性强,实际操作起来却十分复杂;(5)基于Reeb图的思想。如图3所示,该算法首先在模型上定义一个连续函数,计算每个顶点的函数值,将相同函数值的顶点聚合成一个顶点,连接各个聚合后的顶点,形成骨架图。其中最著名的是Hilaga等人提出的多分辨率Reeb图 (Multiresolutional Reeb Graph,简称MRG) 算法[5],它可以表示不同分辨率级别的3D形状的骨架和拓扑结构。图3表示了不同分辨率的Reeb图,在模型上定义一个连续函数U,通过三种不同分辨率来计算Reeb图,由图可见,函数区间分割的层次越多,所得的Reeb图越精确。
另外,国内外的其他学者也对物体的骨架提取技术进行了一些研究。意大利学者Jacopo Aleotti[6]通过摄像机观测三维物体,将三维物体拓扑分解成若干部分,从而实现骨架的提取;葡萄牙学者Diego R. Faria[7]提出了两种模型拓扑分离方法:基于物体主轴的分离方法和基于高斯混合模型的分离方法,结果发现后者运算效率低,花费时间长,采用基于主轴的分离方法效果要好;国内学者宫法明[8]提出了基于特征点求解的骨架提取算法,能够快速的提取出模型骨架,但对于复杂的模型还存在过多的问题。
提出了针对三角网格模型的骨架提取算法,首先对复杂的三角网络进行简化处理,然后遍历所有的三角形,采用Dijkstra算法抽取基本点集,根据定义的Morse函数计算每个顶点的函数值,最后根据函数值得出模型的基本骨架。算法的程序流程图如下所示:
1 读入模型文件
STL文件是在计算机图形应用系统中用于表示三维网格模型的一种文件格式[9]。三维模型采用STL文件格式进行表达。
以vs2010为平台,运用VTK开源软件包面向对象原理设计和实现算法。VTK自身提供了一种进行网格读取的方法,它是将一个模型三角网格的所有顶点坐标以及它们的索引号直接在程序中表达出来,然后通过循环遍历读取每一个网格及顶点。这种方法具有局限性,只适用于三角网格所有顶点坐标以及每个点的索引号已知的情况下,模型三角网格的读取。而大量的三维模型网格复杂,无法得到模型三角网格所有顶点以及索引号,这时就需要利用程序读取模型的网格信息。
旨在设计出一种针对任意模型,可以读取三角网格信息的算法,这样可以处理的模型范围广泛,也能精简程序的长度,以长方体为例进行说明。
长方体有8个顶点,6个面,对应的STL文件中有8个顶点和12个三角形网格。图5是一个长方体的三角网格模型,每个面被分成了两个三角网格。取其中一个三角网格进行分析,它包含了3个顶点,每个顶点对应着一个索引号。所以,如果想要完全表达这个长方体,分为两个步骤:1.从某一个顶点开始遍历所有的顶点,给出顶点的三维坐标,并将索引号与每个顶点相对应;2.从某一个三角网格开始遍历所有的三角网格,并给出每一个网格顶点的索引号。
根据以上的分析,可以列出求解各个顶点三维坐标的程序:
如图6所示,其中i代表第i个顶点,N代表总顶点数,Pi[3]代表第i个顶点的三维坐标,而vId代表该顶点对应的索引号。三维STL文件导入后,由第一个顶点开始遍历,遍历每个顶点时,输出顶点的三维坐标,然后将每个顶点的索引号与坐标相对应,直到遍历完所有的顶点。
同样的思路,也可以列出求解网格数据的程序流程图,如图7所示。
在图7中,j代表第j个网格,M代表总网格数目,k代表第j个网格的第k个顶点。GetCellPoints()将每个三角网格的顶点提取出来,然后根据提取出来的顶点进行二次遍历。GetId(k)将第k个顶点的索引号提取出来。依次循环遍历,直到遍历完所有的网格。
用上述方法提取出长方体每个索引号对应的顶点坐标,如表1所示。(P—顶点索引号)
上述长方体共有12个三角网格,每个网格对应三个顶点,每个三角网格对应三个顶点的索引号如表2所示。(M—三角网格序号)
这样,就将长方体模型的几何特性完全表达了出来,为后续研究提供了前提。
2 三维模型网格的简化
导入网格文件后,为了便于后续处理,需要先对三维模型进行简化,采用OpenGL中使用层次细节(level of details,缩写LOD)方法来实现[10]。
LOD方法运用最多的有两种算法,分别是压缩三角形算法和折叠三角形算法[11]。对于第一种算法,是将要简化的三角形网格的三个顶点压缩至一个点,实现网格的简化。如图8所示,△M1M2M3是要压缩的三角形,将三角形的三条边设为0,则△M1M2M3就变成了点M。
对于第二种算法,基本思路是将两个三角形的共线端的两顶点重合,使两个三角形折叠,从而达到简化三角形网格的效果。如图9所示,要简化△N1M1M2和 △N2M1M2,将顶点M1和M2重合至顶点M,则边L1、L2、L3和L4也重合至边L。
对比两种算法,折叠三角形算法可以同时简化两个三角形,运用此方法,迭代简单,运行速度快,采用这种算法进行复杂模型的简化。
本算法在OpenGL平台上实现,基本数据结构由Vertex,Triangle,Process三个结构体组成,如下所示:
struct Vertex
{
GLfloat k[]=new GLfloat[3]; //顶点的三维坐标
GLint vId; //顶点的索引号
}
struct Triangle
{
Glint tId; //三角网格的索引号
Bool t_flag; //标识该三角网格是否被刪除
GLTVector3 t_normal; //三角网格法向量
}
struct Process
{
GLint process[]=new GLint[4]; //顺序存储了一次简化操作中除去的点、三角网格的索引号
