基于代理模型的固体动力杀伤器气动外形优化研究

龙永松 王伟 刘玉祥

摘   要：分析了固体动力杀伤器的气动外形设计参数。通过进化神经网络构建气动外形参数与气动特性之间的代理模型，然后确定了气动外形优化方法，并完成了算例验证。结果表明：通过代理模型开展固体动力杀伤器气动外形优化是可行的，能够大大缩短杀伤器气动外形优化周期。

关键词：固体动力杀伤器;气动外形优化;代理模型

中图分类号：V423.9                                          文献标识码：A

文章编号：1003—6199（2020）02—0042—04

Abstract：The aerodynamic shape design parameters of solid kinetic killer（SKK） are analyzed firstly，and the surrogate model between aerodynamic shape parameters and aerodynamic characteristics is constructed by evolutionary neural network. Then，the aerodynamic shape optimization method is determined and verified by an example. The results show that it is feasible to optimize the aerodynamic shape of the SKK by surrogate model，and it can greatly shorten the optimization cycle of the aerodynamic shape of the SKK.

Key words：solid kinetic killer;aerodynamic shape optimization;surrogate model

固体动力杀伤器（以下简称“杀伤器”）工作在高度20 km以上，甚至大气层外，跨越了连续流、过渡滑移流、稀薄大气以及大气层外的空间，飞行空域跨度大。飞行速度从超声速到高超声速，速域跨度也比较大。另外，杀伤器还通常采用直接力控制，存在复杂的侧向喷流气动干扰等问题。因此，杀伤器气动外形设计过程中工作量大，周期长，传统的气动建模方式难以适应快速设计的需要，需要引入新的建模手段或设计方法，达到快速、精确设计的目的。

采用代理模型是目前解决以上难题的有效方法之一[1]。代理模型是指通过数学手段构造的工作量小、计算结果与试验结果近似的数学模型，可以代替试验模型用于优化设计[2]。相较于数值计算和地面试验，代理模型在保证较高模型精度的同时，还具有计算量小、求解迅速、不依赖硬件设施等一系列优点。国内外对代理模型的研究从20世纪90年代，研究人员对代理模型构建技术的研究热情一直以来处于持续升温的过程，特别是近10年来，代理模型在航空、汽车、船舶等行业的结构设计、流体分析以及多学科设计优化等方面得到广泛的应用和深入的发展[2-9]。

1   气动外形设计参数

固体动力杀伤器（以下简称“杀伤器”）的气动外形主要为锥-柱-群和多锥等形式，通常采用姿控和轨控直接力对其姿态进行控制。它的气动外形可采用6个参数进行描述（图1），包括锥段1扩张角δn，锥段1直径d，锥段2扩张角δb，锥段3扩张角δt，全彈长度L，全弹最大直径D。

在δn、d、L、D不等于0前提下，根据δb、δt取值的不同，杀伤器外形可描述为以下几种形式：

a）当δb=0、δt≠0时，外形为锥-柱-裙布局;

b）当δb=0、δt=0时，外形为锥柱布局;

c）当δb=δt≠0时，外形为双锥布局;

d）当δb ≠ 0，δt ≠ 0，且δb ≠ δt时，外形为三锥布局。

杀伤器气动设计目的是确定气动外形参数，获得气动特性矩阵C（cx1，cy1，cz1，xcp，mx1，my1，mz1），具体定义见表1。

2   代理模型构建

代理模型的构建可以采用线性插值、克里金插值、神经网络等。考虑到样本的数量和对精度的要求，本文以进化神经网络构建杀伤器气动外形参数与气动特性数据之间的代理模型。

进化神经网络[10]（evolutionary neural networks，ENN）是基于进化计算和神经网络两大智能分支，将二者有机融合在一起产生的一种全新神经网络模型，克服了神经网络容易不收敛和进化算法进化时间长的不同缺点。进化神经网络的进化策略主要分为两种：进化规划与遗传算法。考虑到遗传算法的简便有效，进化策略选定为遗传算法。另外，根据进化神经网络的三个等级，进化神经网络模型的发展呈现以下四个不同的类型：连接权值进化的进化神经网络;网络结构进化的进化神经网络;结构和权值同时进化的进化神经网络;学习规则进化的进化神经网络。主要从连接权重进化的角度对进化算将网络进行训练。

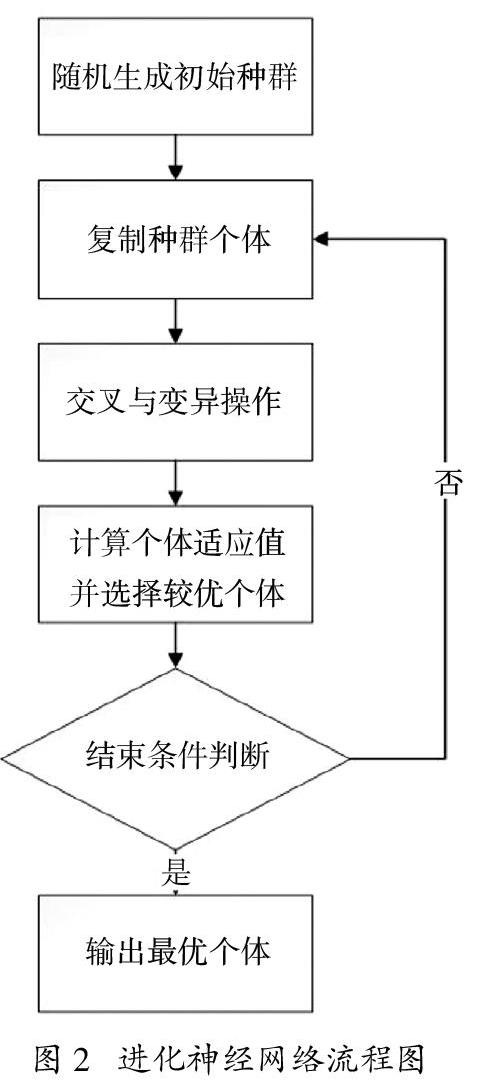
进化神经网络具体操作流程图如图2，首先随机生成初始种群，初始种群的每个个体都是一个待优化的神经网络。通过复制、交叉与变异的遗传操作，由父代生成子代，计算父代与子代的个体适应值，选择两代个体中的较优个体，生成新一代种群。对新种群进行判断，判断迭代次数是否满足要求或个体适应值是否满足要求值。

进化神经网络构建代理模型的步骤如下：

第一步、设定算法基础参数

设定迭代代数为100，在100代后结束迭代过程。交叉概率设定为0.4，变异概率设定为0.2。

第二步、设定神经网络模型

设定神经网络的输入层为六个节点，分别对应六个气动外形数据，（锥角一，锥角二，锥角三，直径一，全弹长，全弹最大直径）。设定神经网络只有一层隐含层，根据上文所述，设定隐含层节点数为17。输出层为4个节点，分别对应四个气动特性。

第三步、建立适应度函数

适应度函数分为两部分：模型误差和设计经验。以仿真数据库中的仿真数据作为输入，通过算法模型得到预测输出，比较预测输出与实际输出之间的误差，即模型误差。生成两组对比样本，其中一组样本包涵有设计经验，通过对比的方式，得到被测试模型是否含有设计经验。

第四步、生成初始种群

随机生成（0，1）范围内的初始个体，每个个体是一个单行170列的矩阵，矩阵元素对应了神经网络的连接权值。

第五步、完成遗传操作

在构建代理模型的基础上，利用20个气动外形方案的20组气动特性数据对代理模型进行了训练，得到高精度的代理模型。

3   气动外形优化方法

杀伤器气动外形设计的目标可以描述为：

●   静稳定裕度随飞行马赫数变化范围

●   满足约束条件的情况下，有效容积越大越好（越大越好，作为目标函数）

●   阻力系数越小越好

●   法向力系数越大越好

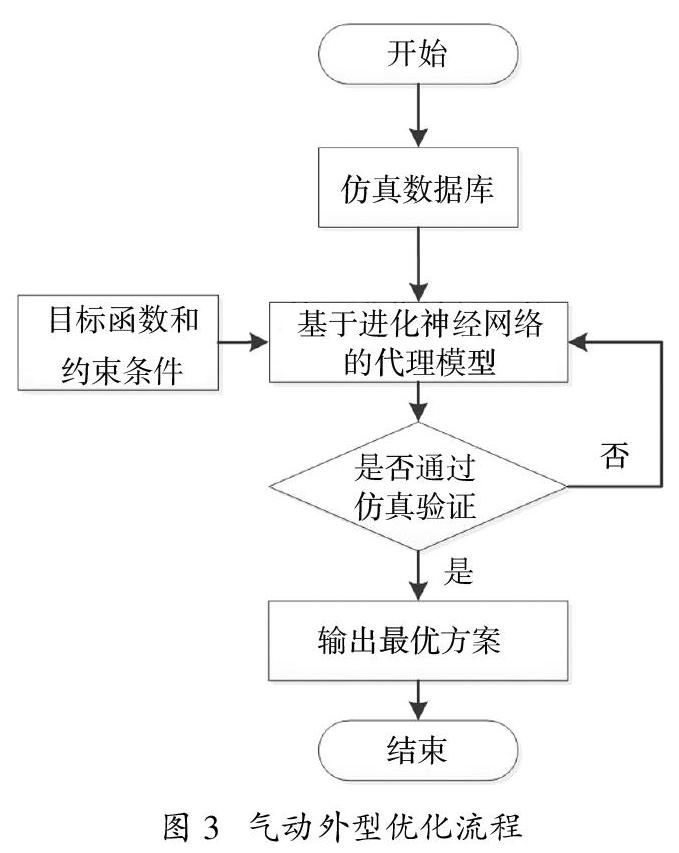
在杀伤器气动外形设计时，将目标函数和约束条件输入代理模型，不断进化学习、迭代，最终得到最优方案，优化过程如图3所示。

a）优化参数集

优化参数集主要是杀伤器的外形参数，如表2所示。

b）目标函数

将容积作为目标函数，容积的数学表达式为：

其中H表示锥段2的长度，表达式为：

其中d为锥段1直径，D为全弹最长直径。

c）约束函数

将杀伤器总体设计中的限制条件，作为进化算法中的约束函数，如表3所示。当设计结果的气动特性不满足约束条件时，认为该方案不可行;当气动特性满足约束条件时，则认为该方案可行。

其中xcp，表示压心系数，xcg表示质心系数。

4   算例及分析

a）问题描述

选取锥-柱-裙布局外形作为优化对象（锥段2扩张角δb=0），在给定杀伤器最大直径D和长度L的情况下，问题可描述为，Max V容积≥200 000 mm3：

b）计算结果

利用20个气动外形方案的气动数据，对代理模型进行了训练，获得高精度的代理模型，然后对杀伤器气动外形进行了优化，得到如表4所示的最优解及表5所示的优化结果。可看出，通过构建代理模型，利用进化算法可以得到满足设计目标的结果，且优化花费的时间控制在1小时以内，由此可看出，采用代理模型方法，能有效的提高设计效率，缩短杀伤器气动外形设计的时间。

5   结   论

利用气动外形参数与气动特性数据之间的映射规律，通过进化神经网络构建代理模型，对杀伤器的气动外形进行优化。通过算例分析可知，利用代理模型进行气动外形优化是可行的，而且优化计算时间短，能够大大缩短杀伤器设计周期。

参考文献

[1]    SIMPSON T W，BOOKER A J，GHOSH D，et al. Approximation methods in multidisciplinary analysis and optimization：a panel discussion[J].  Structural & Multidisciplinary Optimization，2004，27（5）：302-313.

[2]   TANG X，ZHOU J. Dynamic personalized recommendation on sparse data [J].  IEEE Transactions on Knowledge & Data Engineering，2013，25（12）：2895-2899.

[3]   VENTER G，HAFTKA R，JAMES S J. Construction of response surfaces for design optimization applications [R]. AIAA-96-4040.

[4]    ROUX W J，STANDER N，HAFTKA R T. Response surface approximations for structural optimization [J].  International Journal for Numerical Methods in Engineering，2015，42（3）：517-534.

[5]    KEULEN F V，VERVENNE K. Gradient-enhanced response surface building [J].  Structural & Multidisciplinary Optimization，2004，27（5）：337-351.

[6]    SIMPSON T W，BOOKER A J，GHOSH D，et al. Approximation methods in multidisciplinary analysis and optimization：a panel discussion[J].  Structural & Multidisciplinary Optimization，2004，27（5）：302-313.

[7]    ZHOU Z，ONG Y S，NAIR P B，et al. combining global and local surrogate models to accelerate evolutionary optimization [J].  IEEE Transactions on Systems Man & Cybernetics Part C，2006，37（1）：66-76.

[8]    QIAN Z，SEEPERSAD C C，JOSEPH V R，et al. Building surrogate models based on detailed and approximate simulations[J].  Journal of Mechanical Design，2012，128（4）：963-972.

[9]    BUCHE D，SCHRAUDOLPH N N，KOUMOUTSAKOS P. Accelerating evolutionary algorithms with Gaussian process fitness function models [J].  IEEE Transactions on Systems Man & Cybernetics Part C，2005，35（2）：183-194.

[10]  GUAN Shou-ping，呂欣. 基于过程神经网络的稀疏数据过程建模方法[J]. 系统仿真学报，2008，（11）：2893-2896.