不同ISB处理策略对PPP影响的研究
2022-05-31陈辉
陈辉
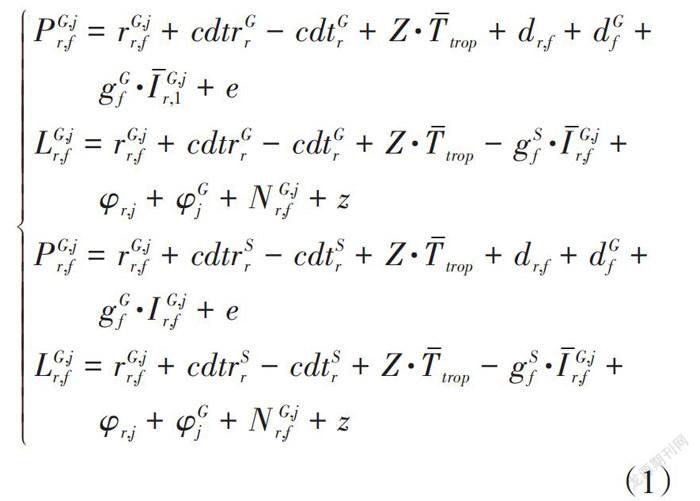
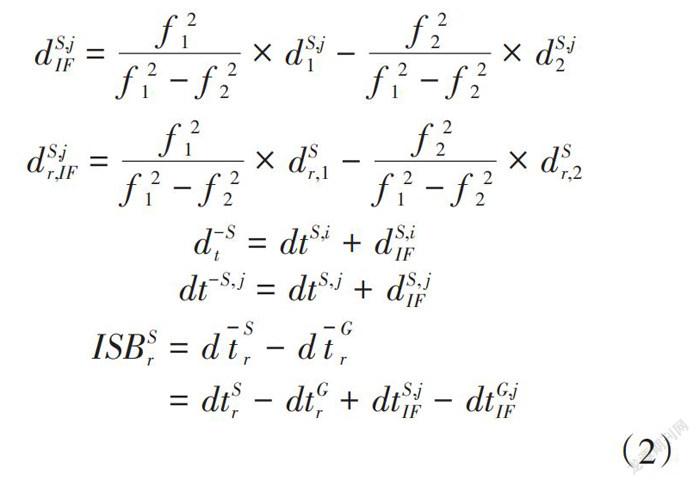
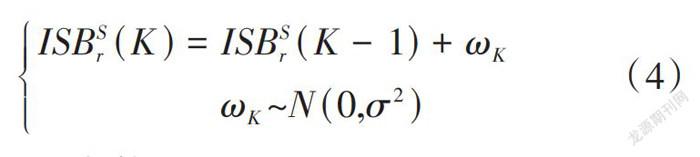
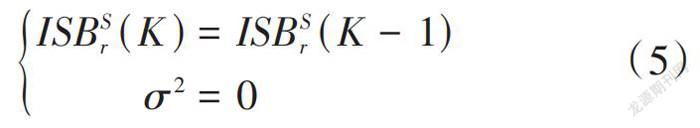
摘 要:多系统组合精密单点定位(Precise Point Positioning,PPP)中系统间偏差(Inter-System Bias,ISB)是必须要考虑的问题。对ISB可以通过参数估计进行消除,由于参数估计有多种策略,所以本研究利用MGEX观测站的精密产品,采用不同的估计策略对“GPS+BDS”“GPS+Galileo”组合进行动态、静态解算分析PPP性能,并分析ISB的单天特性。试验表明,采用随机游走和时间常数策略估计获得的ISB稳定性最优,而采用白噪声估计得到的ISB具有较大的波动。对于多系统PPP解算而言,无论是动态还是静态,ISB采用随机游走和白噪声策略可以获得较高的稳定性并减少收敛时间,而采用时间常数进行ISB估计效果较差。
关键词:多系统精密单点定位;系统间偏差特性;参数估计
中图分类号:P207.2 文献标志码:A 文章编号:1003-5168(2022)9-0028-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2022.09.005
The Impact of Different ISB Processing Strategies on PPP
CHEN Hui
(School of Spatial Information and Geomatics and Mapping Engineering,Anhui University of Science and Technology,Huainan 232001,China)
Abstract:Inter-System Bias (ISB) in The Multi-System Precise Point Positioning (PPP) is a problem that must be considered.For ISBs can be eliminated by parameter estimation,since there are multiple strategies for parameter estimation,this paper uses the precision products of MGEX observatories to use different estimation strategies to analyze the dynamic and static solution of GPS+BDS,GPS+Galileo combinations to analyze PPP performance,and analyze the single-day characteristics of ISBs.Experimental results show that the ISB stability obtained by random walking and time constant strategy estimation is optimal,while the ISB obtained by white noise estimation has large fluctuations.For multisystem PPP solutions,whether dynamic or static,using random walk and white noise strategy can obtain high stability and reduce the convergence time, while using time constant for ISB estimation is less effective.
Keywords: Precision Point Positioning; Inter-System Bias; parameter estimation
0 引言
随着BDS卫星系统的快速发展,多系统GNSS并存与发展的局面逐渐形成,多系统卫星组合逐渐成为新的发展趋势[1-2]。与单系统相比,多系统PPP可以增强卫星可用性、优化卫星空间结构、缩短收敛时间,且有利于提升定位精度[3]。但在多系统组合应用过程中,由于各系统的时间基准、坐标系统不同以及硬件延遲、信号解码等方面的差异产生系统间偏差(Inter System Bias,ISB)[4]。近年来,有大量的学者对ISB进行了研究。Tegedor等[5]通过对GPS、BDS、Galileo的ISB进行系统分析,发现ISB与接收机有关。Li等[6]使用常数对ISB进行估计,并进行多系统PPP的比较分析。Li等[7]和Bakker等[8]使用随机游走和白噪声对ISB进行估计。Li等[9]利用GPS/GLONASS组合,使用随机游走和白噪声模型对ISB进行估计。
随着北斗卫星的升空组网,以及多频数据的播发,这为多系统GNSS带来了新的挑战,研究多系统条件下合理估计ISB至关重要。本研究采用全球分布的10个MGEX测站提供的数据,并结合精密星历和钟差产品,采用白噪声、随机游走过程和时间常量3种参数估计法对ISB进行估计提取。从坐标收敛时间和三维定位精度两个方面来分析不同ISB处理策略对多系统GNSS非差非组合PPP定位的影响。
1 基于ISB的非组合PPP函数模型
非组合PPP以伪距和载波观测值为原始观测值,其观测方程如式(1)。
[PG,jr,f=rG,jr,f+cdtrGr-cdtGr+Z·Ttrop+dr,f+dGf+ gGf·IG,jr,1+eLG,jr,f=rG,jr,f+cdtrGr-cdtGr+Z·Ttrop-gSf·IG,jr,f+ φr,j+φGj+NG,jr,f+zPG,jr,f=rG,jr,f+cdtrSr-cdtSr+Z·Ttrop+dr,f+dGf+ gGf·IG,jr,f+eLG,jr,f=rG,jr,f+cdtrSr-cdtSr+Z·Ttrop-gSf·IG,jr,f+ φr,j+φGj+NG,jr,f+z]
(1)
式中,[P]和[L]表示卫星伪距和载波观测值;上标G表示GPS系统;[S]表示其他卫星系统([S=R,E,C]);[j]表示卫星PRN;下标[r]表示接收机;[f]表示卫星频率数;[r]表示卫星至测站空间几何距离;[cdtr]表示接收机钟差;[cdt]表示卫星钟差;[dr,f]和[dGf]分别表示接收机和卫星伪距硬件延迟;[φr,j]和[φGj]分别表示接收机和卫星载波硬件延迟;[Z]表示对流层延迟映射函数;[T]表示对流层延迟;[I]表示电离层延迟;[g]表示与信号频率有关的系数;[e]和[z]分别表示未校准模型化误差。
式(1)可以具体表达为式(2)。
[dS,jIF=f21f21-f22×dS,j1-f22f21-f22×dS,j2]
[dS,jr,IF=f21f21-f22×dSr,1-f22f21-f22×dSr,2]
[d-St=dtS,i+dS,iIF]
[dt-S, j=dtS, j+dS, jIF]
[ISBSr=dtSr-dtGr=dtSr-dtGr+dtS,jIF-dtG,jIF]
(2)
式中,[dSr,IF]和[dS,jIF]表示消电离层组合的接收机和卫星钟差;[dtSr]和[dtS,j]表示吸收消电离层延迟后的接收机和卫星钟差;[ISBSr]表示组合中的系统间偏差。
假设测站在某历元时刻可以接收到m颗卫星,则GPS/BDS/Galileo卫星非组合PPP的观测方程中待估参数为式(3)。
[X={x,y,z,cdtr,ISBSr,T,I,N}] (3)
式中,[ISBSr={ISBCr,ISBEr}]。
2 ISB处理策略
卡尔曼滤波对PPP中的待估参数通常使用随机模型进行估计得出结果,随机模型根据原理不同可分为随机游走、时间常数、白噪声。
2.1 随机游走
在使用随机游走进行ISB估计时,可认为当前历元估值和前一历元具有相关性,考虑到ISB随时间的变化,认为ISB随时间变化的部分[ωK]服从方差[σ2]的正态分布,方差设置为1 mm2。具体表达为式(4)。
[ISBSr(K)=ISBSr(K-1)+ωKωK~N(0,σ2)] (4)
2.2 时间常数
在ISB使用时间常数进行估计时,通常不考虑ISB随时间的变化,设置[ωK=0],表达公式为式(5)。
[ISBSr(K)=ISBSr(K-1)σ2=0] (5)
2.3 白噪声
在使用白噪声进行ISB估计时,通常认为各历元间的ISB没有相关性,所以当每个历元的参数进行滤波状态更新时都赋予一个先验方差,表达式为式(6)。
[ISBSr(K)=N(0,σ2)] (6)
3 试验分析
为了系统地分析不同的ISB估计策略对PPP的影响,本研究选取MGEX的10个观测站在2020年3月1日的观测数据。结合WHU发布的精密钟差轨道产品,同时以sinex文件为参考坐标真值。分别使用随机游走、参数估计和白噪声三种策略对PPP进行解算,评估动态和静态条件下的性能表现。
本研究分别进行静态、动态PPP两种试验,并从三维定位精度和收敛时间两方面进行分析,并定义E、N、U三方向的定位偏差优于1 dm,同时只有在连续20个历元的偏差都满足限制要求时,才认为当前的滤波收敛[10]。
3.1 静态PPP分析
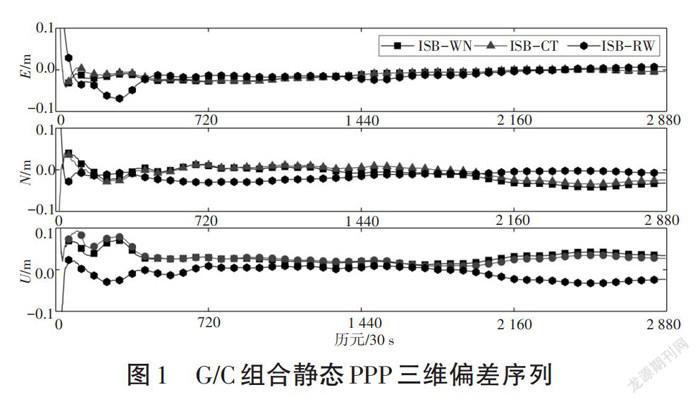
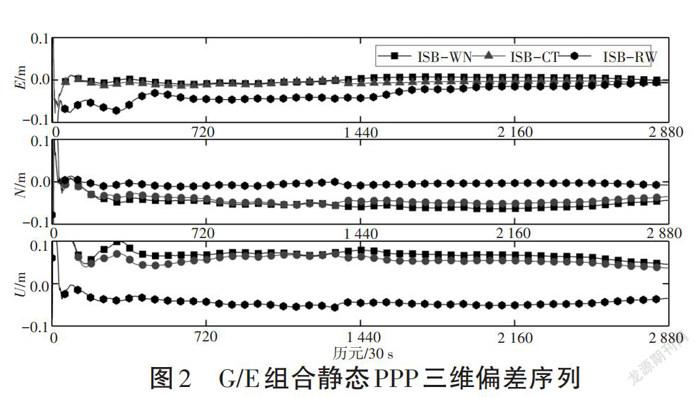
在静态PPP分析中,以FFMJ站为例,统计“GPS+BDS”“GPS+Galileo”组合的北、东、天三维方向的偏差序列,结果见图1、图2。
从图1可以看出,G/C组合在E和N方向上使用白噪声和时间常数得到的解算精度非常接近,基本处于重合状态,而随机游走策略解算效果则优于另外两种。至于G/E组合(见图2)可以發现采用随机游走估计策略计算得到的时间序列最为平滑,然后依次是白噪声、时间常数,这表明在静态PPP时,ISB参数估计可以优先选择ISB-RW和ISB-WN两种策略。因为和ISB-CT相比,另外两种模型可以很快稳定收敛,同时收敛之后波动较小,稳定性较高。
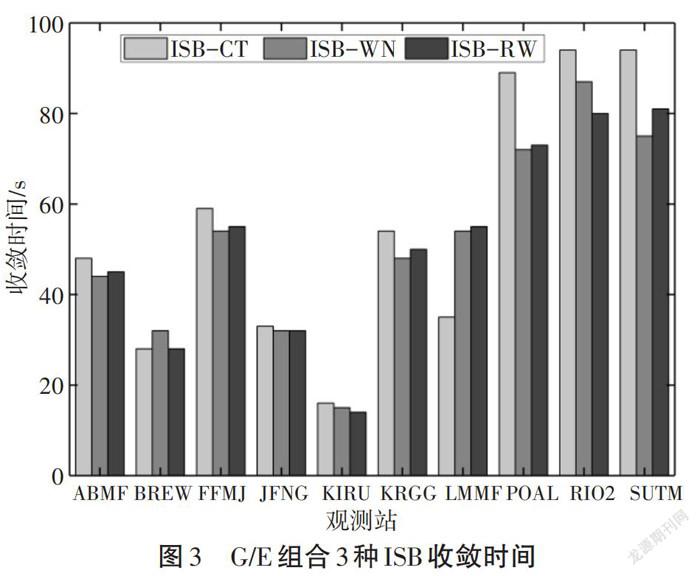
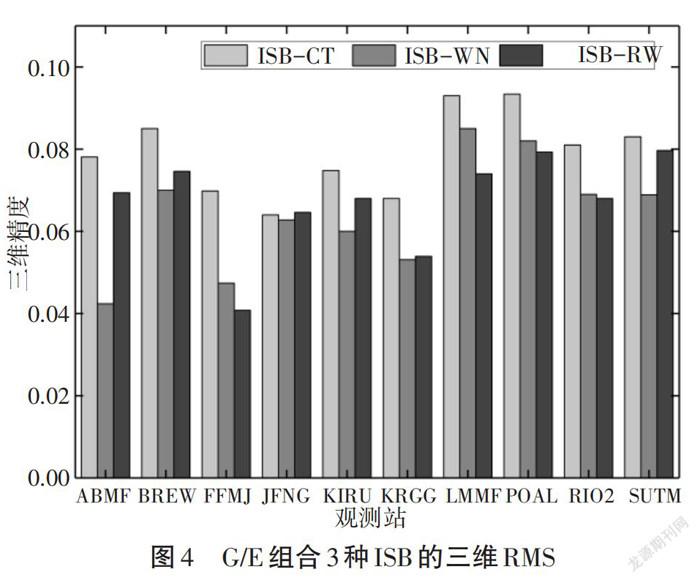
图3和图4分别为G/E组合卫星静态PPP采用三种策略后的收敛时间和三维收敛精度。可以看出除去某些测站外,整体上采用时间常数估计达到收敛的时间较长,且收敛后的三维精度和另外两种策略相比较差。
3.2 动态PPP分析
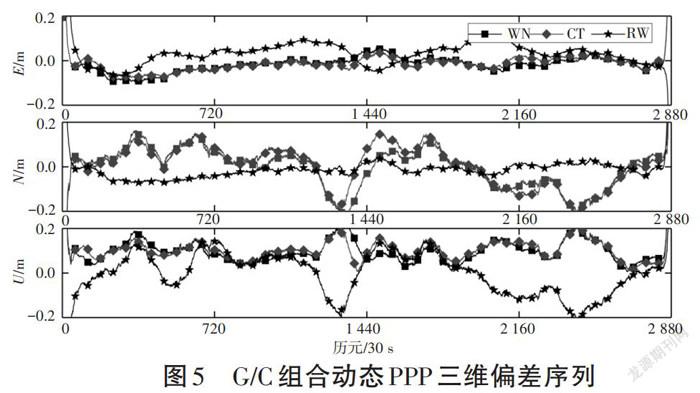
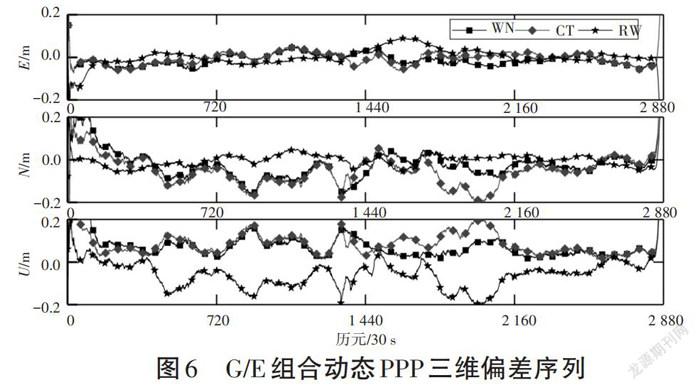
图5和图6分别为动态PPP模式下FFMJ站“GPS+BDS”“GPS+Galileo”组合下的E、N、U偏差时间序列。
从图5和图6中可以发现,动态情况下取得的效果与静态条件下类似。随机游走策略的方向精度稳定性较高,具有明显效果。以N方向和U方向偏差为例,发现使用时间常数估计得到结果波动较大,表明采用此种方法效果不太理想。
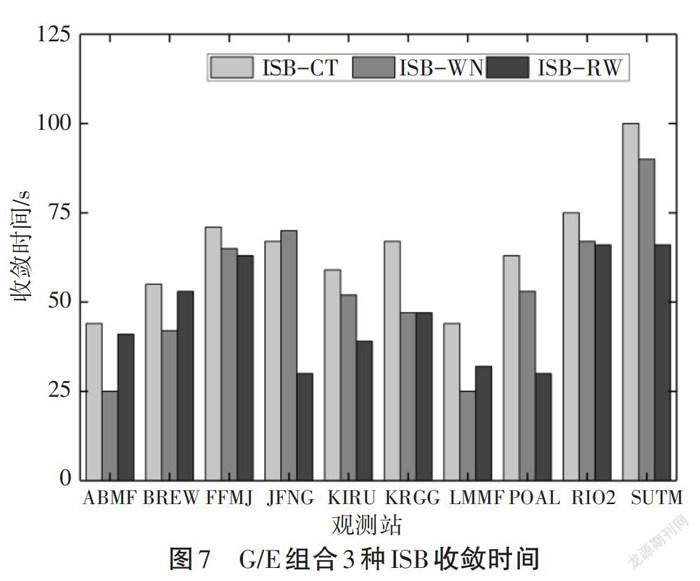
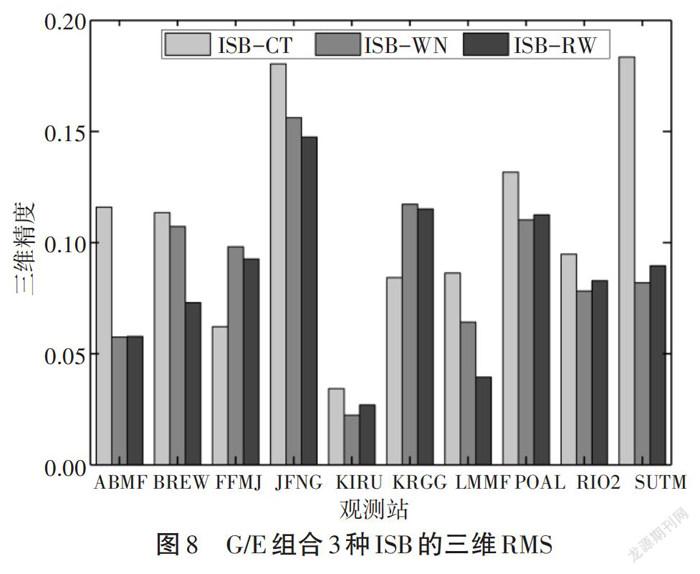
图7和图8分别为G/E卫星组合动态PPP采用三种策略后的收敛时间和三维收敛精度。可以看出除SUTM和BREW等观测站外采用随机游走和白噪声策略的收敛时间和三维精度基本一致。而采用时间常数得到的结果差于另外两种。
4 结语
本研究选取MGEX网中10个观测站的卫星数据,结合WHU发布的精密轨道和钟差产品,使用不同ISB估计策略在“GPS+BDS”“GPS+Galileo”组合条件下进行静态和动态模式的PPP解算。
试验表明,在多系统组合条件下,静态PPP采用随机游走和白噪声这两种策略的精度与时间相近,有些观测站的卫星数据采用随机游走策略优于白噪声。在动态PPP条件下,随机游走策略效果明显最好,采用白噪声策略定位精度略差于随机游走。同时,可以发现与静态PPP一样,时间常数策略取得的效果最差。所以在多系统组合PPP中,可以考虑采用随机游走模型进行ISB的估计。
参考文献:
[1] YANG Y,TANG J,MONTENBRUCK O.Chinese navigation satellite systems[J].Springer International Publishing,2017:273-304.
[2] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010(1):1-6.
[3] 张小红,胡家欢,任晓东.PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J].测绘学报,2020(9):1084-1100.
[4] 王含宇,宋淑丽,周伟莉,等.GNSS偏差及其研究进展[J].天文学进展,2021(1):49-62.
[5] TEGEDOR J,ØVSTEDAL O,VIGEN E. Precise orbit determination and point positioning using GPS, Glonass, Galileo and BeiDou[J].Journal of Geodetic Science,2014.
[6] LI X,GE M,DAI X,et al.Accuracy and reliability of multi-GNSS real-time precise positioning:GPS,GLONASS,BeiDou,and Galileo[J].Journal of Geodesy,2015(6): 607-635.
[7] LI P,ZHANG X.Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning[J].GPS solutions,2014(3): 461-471.
[8] BAKKER P F,TIBERIUS C C J M.Real-time multi-GNSS single-frequency precise point positioning[J].GPS Solutions,2017(4): 1791-1803.
[9] LI P,ZHANG X.Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning[J].GPS solutions,2014(3):461-471.
[10] 慕仁海,黨亚民,许长辉.BDS-3新频点单点定位研究[J].测绘通报,2021(3):12-17.
