一类两性分枝过程条件均值增长率的极限性质∗

宋明珠, 邵 静

(铜陵学院数学与计算机学院，安徽 铜陵 244061)

1 引言

为了描述两性生物繁衍的过程，Daley 在1968 年建立了两性分枝过程的数学模型[1]，引起数学家和生物学家广泛的关注和深入的研究，获得了许多有价值的结果[2-4].事实上，两性生物在繁衍的过程中受众多因素的影响，如：自然环境、社会环境、当前人口数和人口迁移等等.因此，为了更准确地刻画两性生物繁衍的过程，前人建立了一系列比较复杂的模型，如变化环境中的两性分枝过程[5-7]、生物人口可迁移的两性分枝过程[8]、繁衍人口数与当前人口数有关的两性分枝过程[2]以及繁衍数受控制函数控制的两性分枝过程[9-11]，等等.

目前大多数随机环境中的两性分枝过程只研究了概率母函数之间的关系和过程必然灭绝和非必然灭绝的条件.而本文研究的是随机环境中配对依赖人口数两性分枝过程的条件均值增长率的极限性质.本文先给出每个配对单元平均增长率的定义，得到配对单元平均增长率的极限值；再研究条件均值增长率的上、下界，获得了过程条件均值增长率的极限性质，进而推进了前人的研究.

设N 表示非负整数集，N+表示正整数集，(Ω,F,P)是一概率空间，(Θ,B)为任意可测空间.= {ξn: n ∈ N}是定义于(Ω,F,P)上、取值于(Θ,B)的随机序列，{(fξn,i,mξn,i), i ∈N+}是给定环境ξn下取值于N2的独立同分布二维随机变量序列.配对函数Lk(x,y)是定义在N+×N ×N 上、取值于N 的函数，并约定

Lk(0,y)=Lk(x,0)=Lk(0,0)=0.

定义1称序列{Zn,n ≥0}是随机环境中配对依赖人口数的两性分枝过程，若其满足下列条件：

1) Z0=N0, N0是正整数；

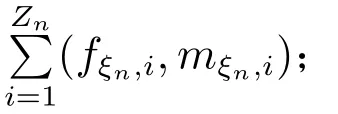
3) Zn+1=LZn(Fn+1,Mn+1)；

其中fξn,i和mξn,i分别表示第n 代第i 个配对单元在环境ξn下生成的雌性和雄性个体数，Fn+1和Mn+1分别表示第n 代所有的雌性和雄性个体总数.

注1易证{Zn,n ≥0}和{(Fn+1,Mn+1), n ≥0}是随机环境中的马氏链.

定义2称随机环境中配对依赖人口数的两性分枝过程{Zn,n ≥0}是上可加的，如果配对函数L·(·,·)是上可加的，即配对函数满足以下两个条件：

(A1) 对固定的k ∈N, Lk(·,·)是上可加的，即

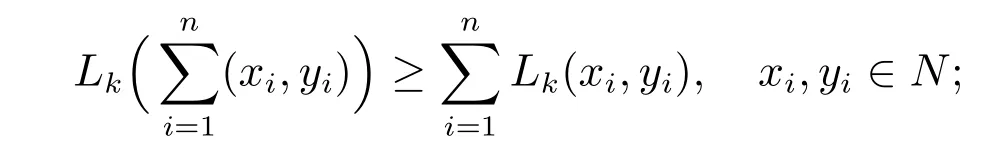
(A2) 对固定的x,y ∈R+, L·(x,y)是上可加的，即

Lj+k(x,y)≥Lk(x,y)+Lj(x,y), j,k ∈N+.

注2k 对配对单元在一起繁衍的后代数，肯定比每个配对单元独自配对繁衍的后代数多，因此配对函数的上可加性符合两性生物繁衍的实际情况.

由注1 可知：对任意的k ∈N+, n ∈N, E(Zn+1|Zn= k, −→ξ )只与k, ξn有关，故有以下定义.

2 配对单元平均增长率的极限性质

定理1

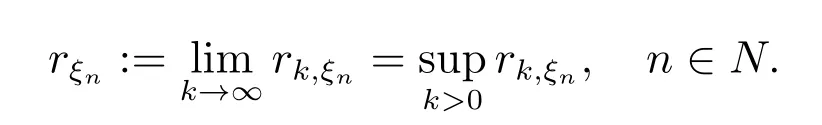
证明 由rk,ξn的定义、L·(·,·)的上可加性以及{(fξn,i,mξn,i),i ≥1}在ξn下是独立同分布的，有

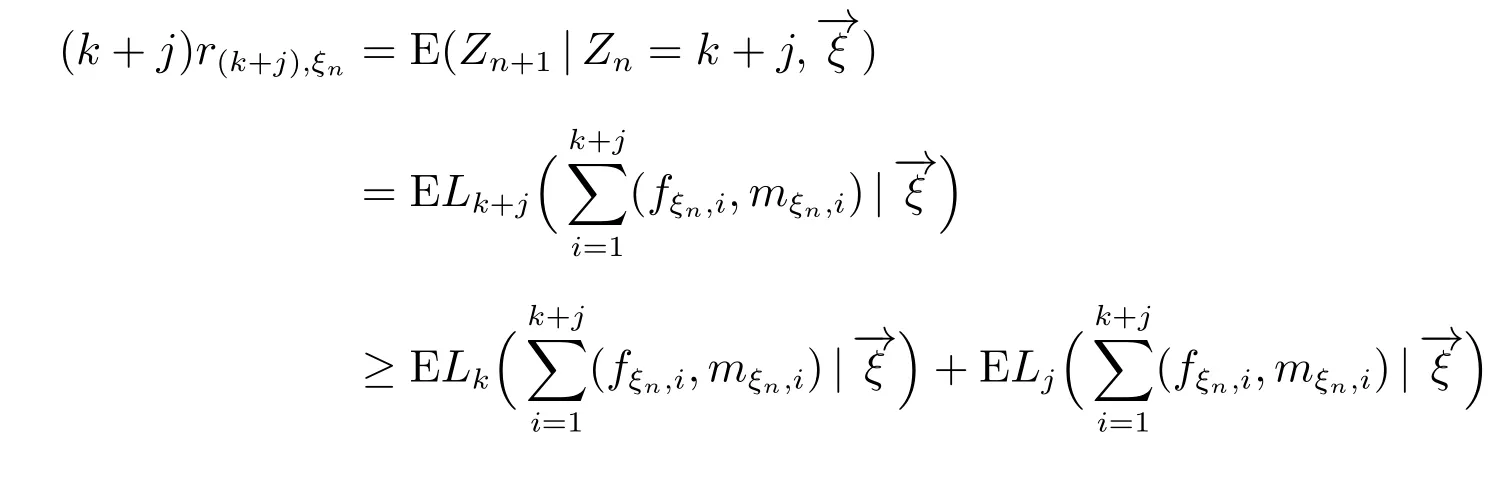
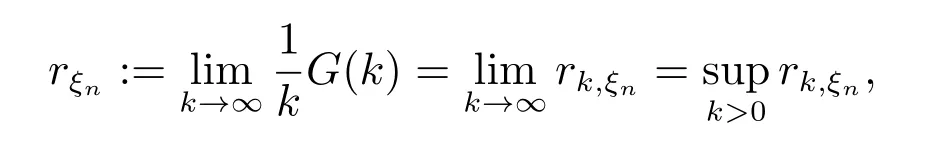
定理1得证.

定理2

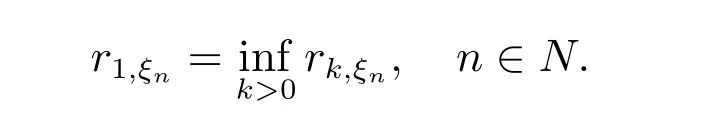
证明 由rk,ξn的定义、L·(·,·)上可加性知，对任意的k ∈N+，有

所以

推论1

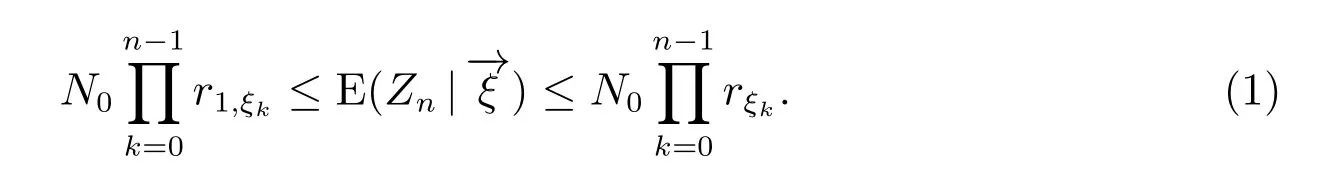
证明 因为

所以，由定理1 和定理2 知

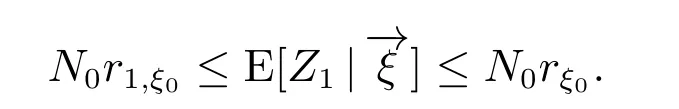
对任意的n ≥2，我们有

同理可得

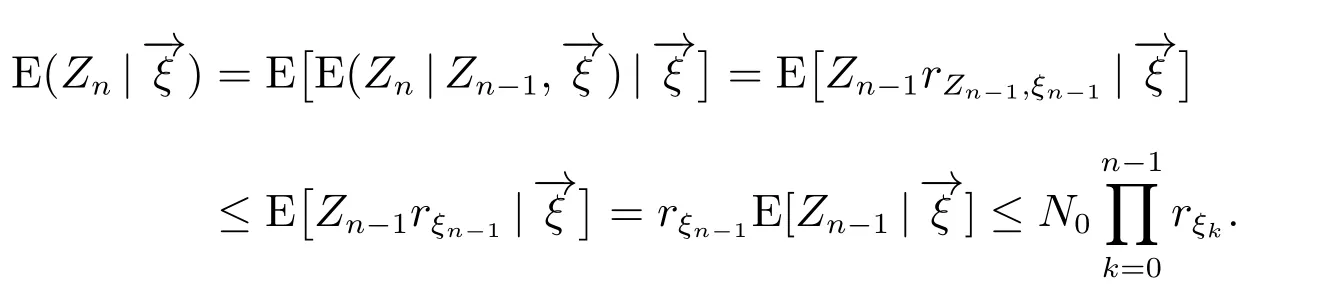
推论1得证.

注3由上述过程知，r1,ξn, rξn是配对单元平均增长率rk,ξn的下、上界，虽然我们没有给出过程{Zn,n ≥0}条件均值E(Zn|−→ξ )的具体数学表达式，但由推论1 可知，

令

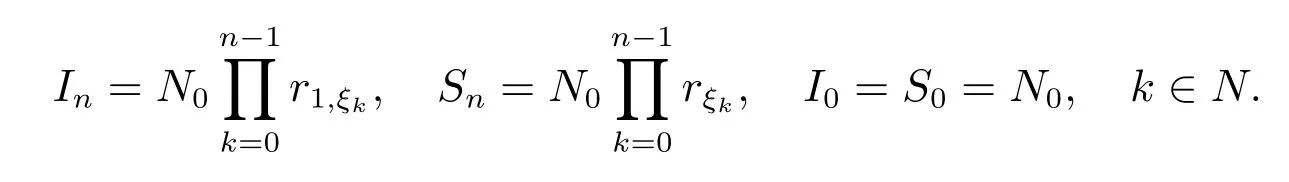
定义序列如下

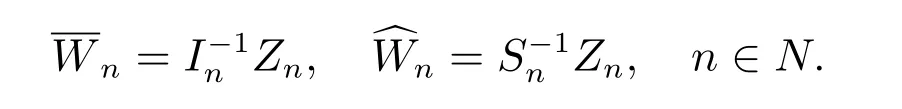
引理1[4]对固定的n ∈N，若{rk,ξn,k ≥1}是非降序列，则存在定义在正实数的非降函数序列fξn(·)，使fξn(k)≤rk,ξn, k ≥1，且f∗ξn(x):=xfξn(x)是凸函数.

注4当x ≥1 时，令

因r[x],ξn是非降序列，易证

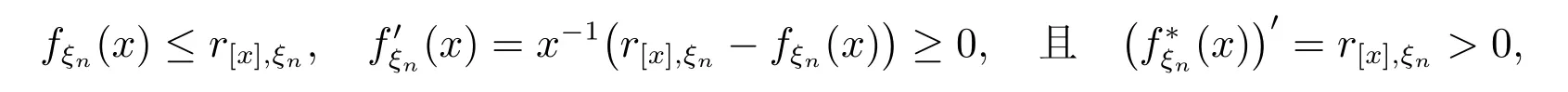
即引理1 得证.下文中涉及的fξn(·)就是引理1 所提及的fξn(·).

定理3设

证明 因为{Zn,n ≥0}是随机环境中的马氏链，由n的定义知

由定理2可知rZn,ξn≥r1,ξn，故E(Wn+1|Fn(−→ξ )) ≥Wn, a.s.，即{Wn,n ≥0}是关

于{Fn(ξ ),n ≥0}的非负下鞅.由推论1 知

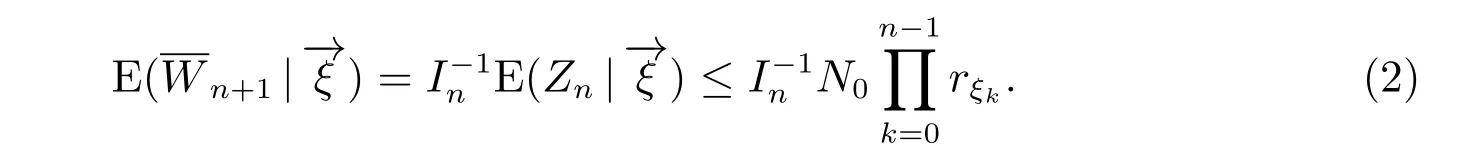
由题设

知

对(2)式两边取期望得

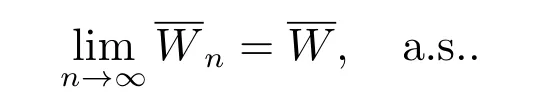
注5从定理3 可知，若

则

由Fotou 引理可得

这表示随着繁衍代数的增加，配对单元平均增长率rk,ξn的下、上界相互逼近，从而使各代的条件均值E(Zn|)增长率相互接近.

定理4序列{n,n ≥0}L1-收敛于非负、有限随机变量W 的充分必要条件是-收敛于一个非负、有限随机变量.则由定理3 的证明过程知，{n,n ≥0}是关于{Fn(),n ∈N}的非负下鞅，所以由题设可得

证明 若

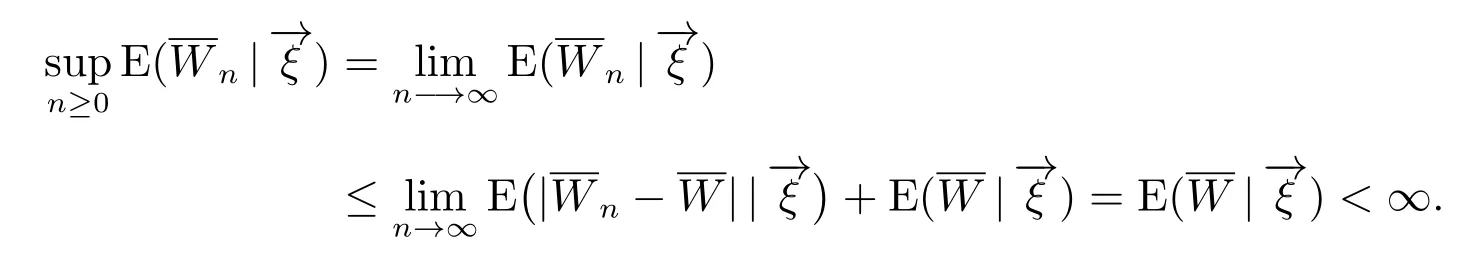
对任意的n ∈N，由引理1 和Jensen 不等式得

由上式递推可得

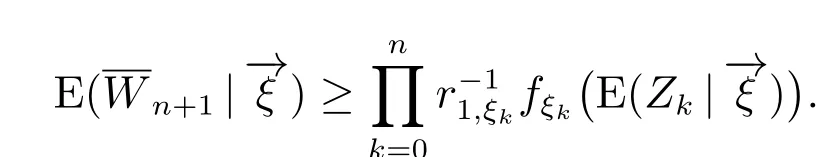
因此

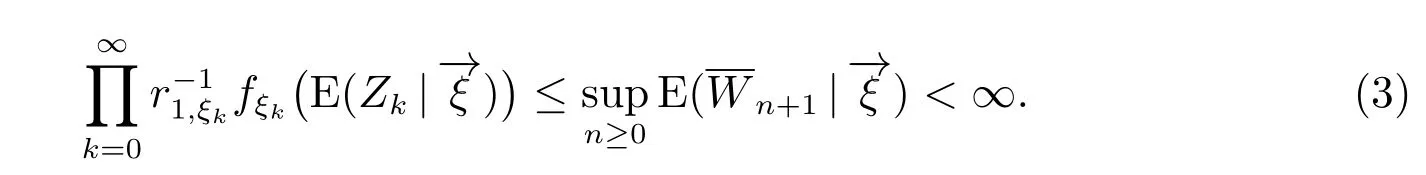
注意到r1,ξk≤rξk，由(3)得

所以

由(3)和(4)可得

即

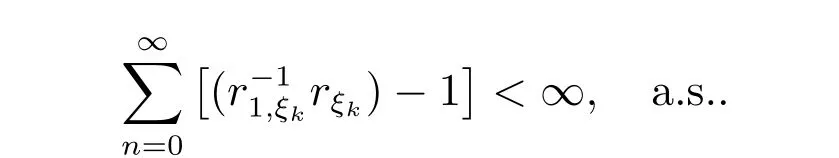
另一方面，若

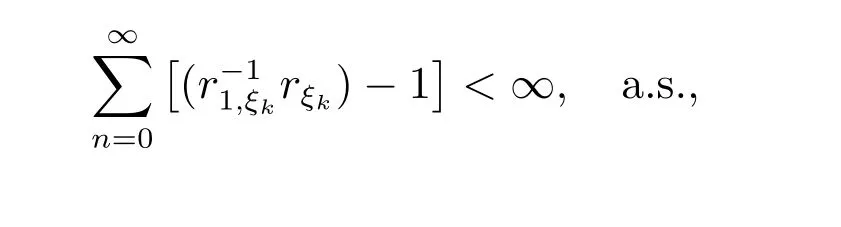
则

所以

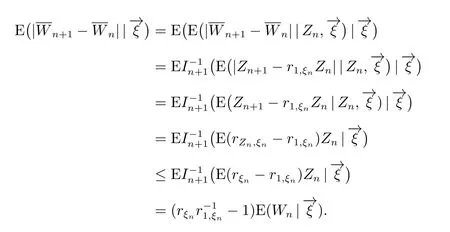
因为

所以

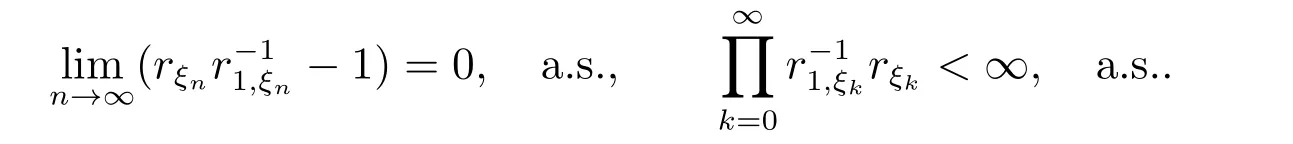
由(1)可得

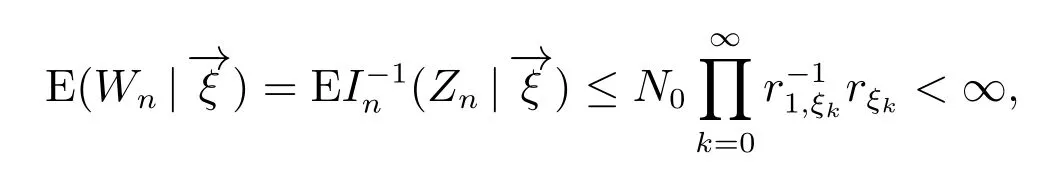
从而

由Fotou 引理得

定理5存在一个有限、非负随机变量，使

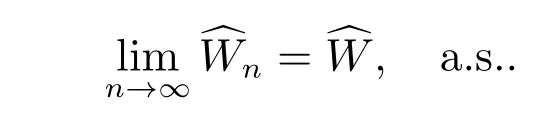
由定理1 可知rZn,ξn≤rξn，所以E(n+1|Fn())≤n，即{n,n ≥0}是关于{Fn(),n ∈N}的上鞅，又因为

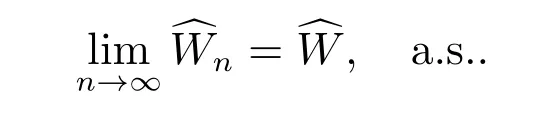
令

则

注6对任意n ∈N，序列{σk,ξn,k ∈N+}有上界.由L·(·,·)的上可加性得

因为

即σξn是序列{σk,ξn,k ∈N+}的一个上界.

定理6若

且独立随机级数的收敛性可以通过Kolmogorov 三级数定理来判定，则存在一正、有限的随机变量^W，使

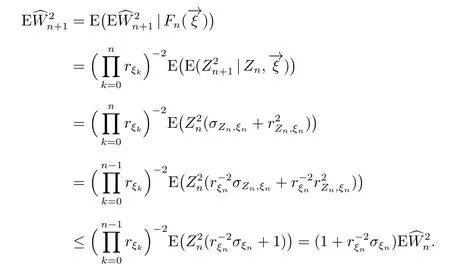
由上式递推得

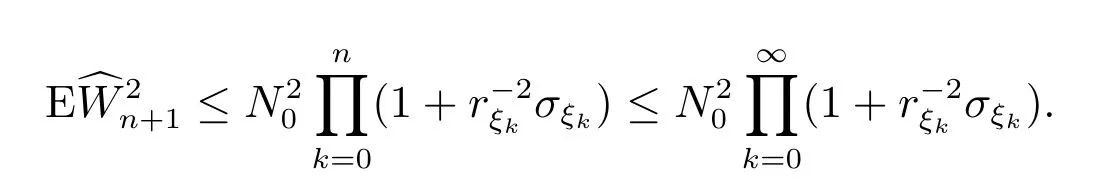
因已知

所以

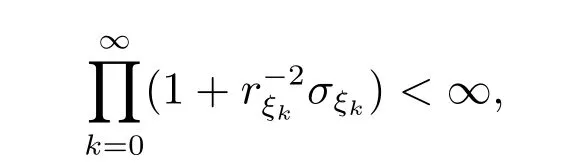
由引理1 可知

由上式递推得

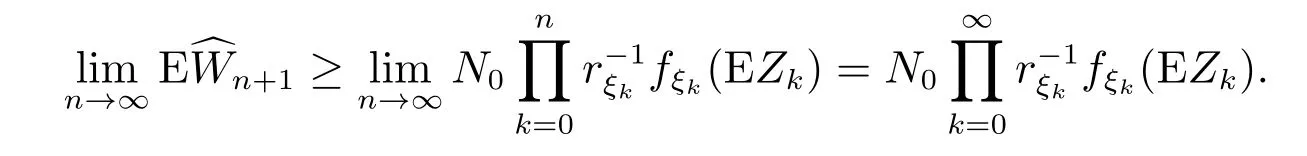
已知

所以

即

定理6得证.