差分进化算法在数字PID参数整定中的应用

2020-07-06孟亚男

吉林化工学院学报 2020年5期

孟亚男,冯兼

(吉林化工学院信息与控制工程学院，吉林吉林 132022)

在工业过程控制中，PID控制策略应用十分广泛，它关系到控制系统性能的优劣[1].而PID控制系统最核心的部分，就是其控制参数.自PID算法问世以来，最普遍的问题就是如何优化整定其控制参数.根据发展阶段可以划分为常规整定和智能整定两大方法，在工业生产中常用的有经验法(试凑法)、衰减曲线法和响应曲线法.在实际生产中，大多数都是根据经验来进行整定.这难免会费时费力，造成一定程度上的浪费，降低生产效率.针对上述问题，介绍一种利用差分进化算法优化整定PID控制参数的方法，仿真结果表明，该方法提高了参数的整定速度和准确度，基本达到了控制的要求.

1 数字式PID控制原理

数字PID是利用计算机软件程序来模拟PID控制算法，数字控制属于采样控制，需要对连续型PID算法做离散化处理.理论上满足采样周期足够短，则离散型控制算法便可以近似处理为连续型控制算法，使控制过程更加灵活实用.经离散化处理后，连续型PID算法各部分可分别用式(1)、(2)、(3)近似替代.

t≈kT，

(1)

(2)

(3)

则离散PID表达可写成式(4)形式：

(4)

数字PID主要分为增量式算法和位置式算法，理论上二者是相同的，但当进行数字量化处理后，二者的实现过程会有所差异.以增量式为例，虽然可以降低误动作的影响，但由于模型的限制，可能会引起较为严重的方法误差，积累到一定程度时会使系统输出严重偏离期望值.综合考虑，本文选用位置型PID算法，方框图如图1所示.

图1 位置式PID控制系统方框图

2 差分进化算法

2.1 基本原理

差分进化算法(DE)属于全局优化算法范畴，其进化流程与遗传算法相似，都是以种群进化为基础的并行搜索算法[2]，图2为DE算法基本流程图[3].一般需要先给定初始种群，计算群体个体适应度，进行初始化操作，再利用变异、交叉和选择等方式不断迭代更新种群，淘汰劣质个体，保留优质个体，有利于逼近全局最优解.

差分进化算法结构简单且易于实现，特别在复杂系统的参数优化问题上，DE算法的表现尤为突出，已经在工业控制等诸多领域得到了应用，实际效果较为满意.

图2 差分进化算法基本流程图

2.2 参数设置

DE算法参数较少，易于理解与实现，主要包括种群规模M、变异算子F和交叉算子CR.变异算子F控制个体向量的扰动程度，决定全局寻优的能力，一般为F=0.3～0.6；交叉算子CR反映了个体间信息交换的程度，一般为CR=0.6～0.9；种群规模M控制种群的多样性和收敛速率，一般为M=20～50.三个主要的参数没有固定取值，各个参数的选择要根据算法的优化目标适当选择[3].

3 基于差分进化算法的PID整定

3.1 目标函数的选取

将“快速—无超调”的性能指标作为系统优化整定的目标，在许多参数优化的系统中，性能指标函数一般都是以系统的e(t)为泛函的积分形式所建立的[4].根据所要达到的性能指标，选择合适的目标函数尤为重要.参考了IAE准则，选用式(5)作为性能指标.

(5)

上式中，以误差绝对值随时间的积分为基础，同时又引入了系统输入的平方项，由于要求所优化整定的系统无超调，采用惩罚功能，即当r(t)-y(t)=e(t)<0时进行优化，将超调量作为最优控制指标的一项，则式(5)可改写为式(6)[5-7].

(6)

式中，e(t)为系统误差；u(t)为控制器输出；w1、w2和w3为权值.

3.2 Matlab实现差分进化算法PID整定

基于以上原理，利用Matlab编写M函数文件进行实验.被控对象的选择如式(7)所示，令系统采样时间Ts=0.001 s，将式(7)转化成式(8)的差分方程形式；考虑到“快速—无超调”的控制要求，采用PID控制方案[8]，输入阶跃响应yd=1，群体规模M=50，令F=1.7，CR=0.8.预先设置Kp∈[0,10]，Ki∈[0,1]，Kd∈[0,2]，有利于全局最优解的搜寻，降低盲目性，w1=0.999，w2=0.001，w3=10.取进化代数G为50.

(7)

y(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_61+num(3)*u_62，

(8)

vi,G+1=ab,G+F·(ar1,G-ar2,G)，

(9)

变异算子的程序实现：从种群中随机取个体ar1,G、ar2,G和ar3,G，且b≠r1≠r2≠r3，以任意整数ri表示个体序号；则变异过程可写成式(9)形式.最优个体用ab,G表示，产生的新个体用vi,G+1表示.则Matlab程序实现如下：

for i=1:N

a=ai(i,:);

n1=1;n2=1;n3=1;n4=1;

while(n1==n2||n1==n3||n2==n3||n1==i||n2==i||n3==i||n4==i ||n1==n4||n2==n4||n3==n4 )

n1=ceil(size * rand(1))；n2=ceil(size * rand(1));

n3=ceil(size * rand(1))；n4=ceil(size * rand(1));

end

v(i,:)=BestS+F*(ai(n1,:)-ai(n2,:));

(10)

交叉算子的程序实现：交叉操作是为了维持群体的多样性，有利于最优解的搜索.具体操作参考式(10)，式中rand∈[0,1]，则Matlab程序实现如下：

for j=1:1:CL

tempr=rand(1);

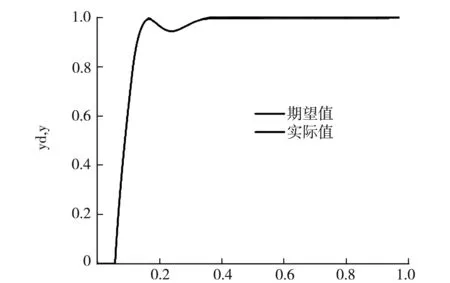
if(tempr

u(i,j)=v(i,j);

else

u(i,j)=ai(i,j);

end

(11)

选择算子的程序实现：根据式(11)可知，分别将ui,G和ai,G代入适应度函数求取适应值进行比较，保留较小的个体[9-11]，则Matlab程序实现如下：

if(Model_1(u(i,:),BsJ)

ai(i,:)=u(i,:);

end

3.3 仿真结果

经过差分进化算法优化整定后，得到实验结果Kp=1.298 2，Ki=0.251 5，Kd=0.052 0，性能指标J=99.897 6，并在Simulink环境搭建控制器模型进行仿真，图3为DE算法整定后的PID响应曲线，其上升时间约为0.35 s，调节时间约为0.486 s；图4和图5分别为性能指标函数J和控制参数的优化趋势曲线，从曲线可以得知，在进化代数为15之后趋于平稳；图6为Simulink仿真曲线，未经优化整定的曲线具有较大超调，约为11.72%，上升时间约为0.228 s，系统余差约为0.031.从仿真曲线中可以看出，采用差分进化算法进行参数整定，系统的各项性能指标较好，且基本达到了“快速—无超调”的目标，仿真结果较为理想.