结构加权相关自适应子空间聚类

李 丹

西安电子科技大学 数学与统计学院，西安 710126

1 引言

随着科学技术的快速发展，大规模高维数据在社会、经济、工程等领域越来越普遍。大规模高维数据不仅增加了数据存储的需求，也使得数据分析更加复杂。子空间聚类[1]的目的是将来自不同子空间的高维数据分割到本质上所属的低维子空间，从而揭示高维数据的低维结构，是处理高维数据强有力的工具。目前，基于谱聚类的子空间聚类方法是聚类分析的研究热点。例如，稀疏子空间聚类（Sparse Subspace Clustering，SSC）[2]、基于低秩表示的子空间聚类（Low-Rank Representation，LRR）[3]、最小二乘子空间聚类（Least Squares Regression，LSR）[4]、光滑表示子空间聚类（Smooth Representation，SMR）[5]、相关自适应子空间聚类（Correlation Adaptive Subspace Segmentation，CA-SS）[6]，还有图像分割的改进稀疏子空间聚类方法[7]、基于加权稀疏子空间聚类多特征融合图像分割[8]、基于相关自适应加权回归的图像分割（Correlation Adaptive Weighted Regression，CAWR）[9]以及基于L0 约束的稀疏子空间聚类[10]，上述这些方法分两步解决子空间聚类问题，首先，从数据中学习自表示矩阵，并用自表示矩阵构造相似度矩阵，第二步利用谱聚类算法获得聚类结果。这种方法虽然取得了较好的聚类结果，但是没有考虑数据相似性度和分割之间的关系。

Li 等[11]提出的结构稀疏子空间聚类（Structured Sparse Subspace Clustering，SSSC）将上述两步合为一步，利用相似度和分割之间的依赖关系，同时得到相似度矩阵和聚类结果。SSSC模型的聚类性能优于上述的两步法，但是SSSC只考虑了标签的一致性，忽略了数据相似度的一致性。

为了解决上述问题，同时获得优化的相似度矩阵和聚类结果，本文引入数据点的相关系数对表示系数施加显式惩罚，当数据相关性较弱时，对表示系数用1-范数正则，使得不相关数据分离；当数据高度相关时，对表示系数用2-范数正则，使得相关数据聚集，保证了系数矩阵的稀疏性和一致性；同时引入子空间的结构范数，充分利用了相似度矩阵和分割的依赖关系，将子空间表示形式表述为结构加权相关自适应子空间聚类（SWCASC）问题。实验结果表明，在常用数据集上，提出的方法优于其他的子空间聚类方法。

2 相关工作

定义1（子空间聚类）给定一组数，记作X=(x1,x2,…,xN)∈Rd×N，设这组数据属于k个线性子空间的并。子空间聚类是指将这组数据分割成不同的类，在理想情况下，每一类对应一个子空间。

在子空间聚类方法中，假设每个数据点均可以用同一子空间的其他数据点线性表示，即X=XZ，其中Z=[z1,z2,…,zN]∈RN×N是X的自表示系数矩阵。考虑到实际数据可能有噪声或者干扰，通常将数据表示为X=XZ+E，其中E表示噪声或者干扰。

为了得到有利于揭示数据子空间属性的自表示，已有方法对自表示矩阵采用不同的约束。稀疏子空间聚类（SSC）采用1-范数以获得每个数据点xi的稀疏表示，模型如下：

其中第一项称为数据拟合项，用于度量表示误差或干扰；第二项称为正则项，用于约束自表示矩阵的结构；λ>0 是调节参数，平衡两项的作用。当子空间独立且数据无噪声干扰时，稀疏表示具有块对角结构。然而，如果来自同一子空间的数据高度相关，稀疏表示会随机选择少量相关数据，而忽略其他相关数据。因此，SSC 不能将高度相关数据很好地分组。LRR 采用核范数惩罚表示系数，模型如下：

当数据是无噪声且子空间独立时，LRR也能保证自表示矩阵具有块对角结构，但是实际数据通常有噪声或干扰，此时LRR通常将相关数据分组在一起，但无法将不相关数据分离。LSR用F-范数来惩罚表示系数，模型如下：

LSR 和LRR 一样，将高度相关的数据分组在一起，但也缺乏稀疏性。

多特征融合加权稀疏子空间聚类用高斯函数定义相似度，对表示系数采用加权1-范数，模型如下：

该模型使相似的数据尽可能参与到数据的自表示中，从而改善稀疏表示过稀疏并且不稳定的局限性。但是高斯权依赖于参数σ，从而影响模型性能。

WCAR采用加权的1-范数和2-范数惩罚表示系数，模型如下：

上述聚类方法都分两步，首先学习自表示矩阵，并由此计算相似度矩阵；然后利用谱聚类算法获得聚类结果。但这些方法没有充分利用相似度和数据类别之间的关系。Li和Vidal提出了结构稀疏子空间聚类（SSSC），充分利用了相似度和数据类别之间的关系，其模型如下：

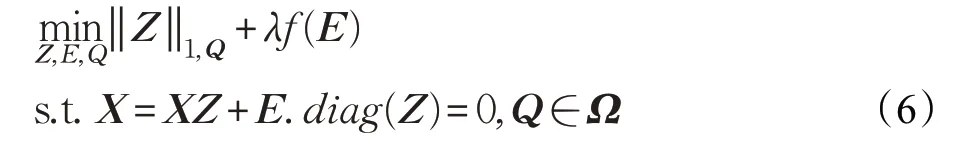
3 结构加权相关自适应子空间聚类（SWCASC）

为了使相似度同时具有稀疏性和一致性，并考虑相似度和分割之间的依赖关系。本文依据数据点的相关性，对表示系数矩阵采用不同约束作为正则项，同时利用相似度与分割之间的关系，对表示系数矩阵采用结构范数，提出了一个新的子空间表示优化模型，称为结构加权相关自适应子空间聚类模型。

其次，为了充分利用数据相似度与分割的依赖关系，本文通过最小化惩罚系数矩阵和分割矩阵，在求解过程中交替迭代求解Z和Q，同时得到学习系数矩阵和相似度矩阵。有效的结合了数据相似度和聚类结果，使得表示系数矩阵和分割矩阵变的一致。

3.1 SWCASC模型

假设数据被2-范数标准化，W⊂ΡN×N是数据点的相关系数矩阵，其中测量数据点xi和xj之间的相关性，称为相关系数。提出的结构加权相关自适应子空间聚类模型如下：

其中，第一项是数据拟合项，第二项和第三项是正则项，分别为加权的显式相关系数惩罚1-范数和2-范数。第四项是结构范数，α>0,β>0 是调节参数。运算符⊙代表Hadamarrd乘积（即对应元素的乘积）。11T是所有元素都是1 的矩阵。一方面，当给定Q时，若wij较大即接近1 时，该模型用2-范数使xi和xj分为一类，当wij较小即接近0 时，该模型用1-范数的稀疏性使xi和xj分到不同类，确保了数据相似度的一致性和稀疏性。另一方面，当给定Z时，若zij≠0 或xi和xj在同一子空间，模型迫使q(1)=q(j)，使得数据有相同标签。该模型可以看做结构化加权的1-范数和2-范数自适应插值，具有自适应性。模型联合标签和相似度矩阵，确保了相似度矩阵的一致性和稀疏性，以及标签的一致性。

对于数据点x，问题（6）可以表述为：

其中，c=(c1,c2,…,cN)T是x的表示系数。

3.2 模型的求解

模型是非凸优化问题，不能直接进行求解。为了得到最优解，交替迭代求解模型。将上述问题分为两个子问题求解：

（1）给定Q，用交替方向乘子法求解Z；

（2）给定Z，用谱聚类方法求解Q。

3.2.1表示系数矩阵Z的求解

为了书写方便，令B=11T-W，问题（7）重写为：

模型（9）等价于：

式（9）的增广拉格朗日[12]函数为：

更新Z，固定S,J：

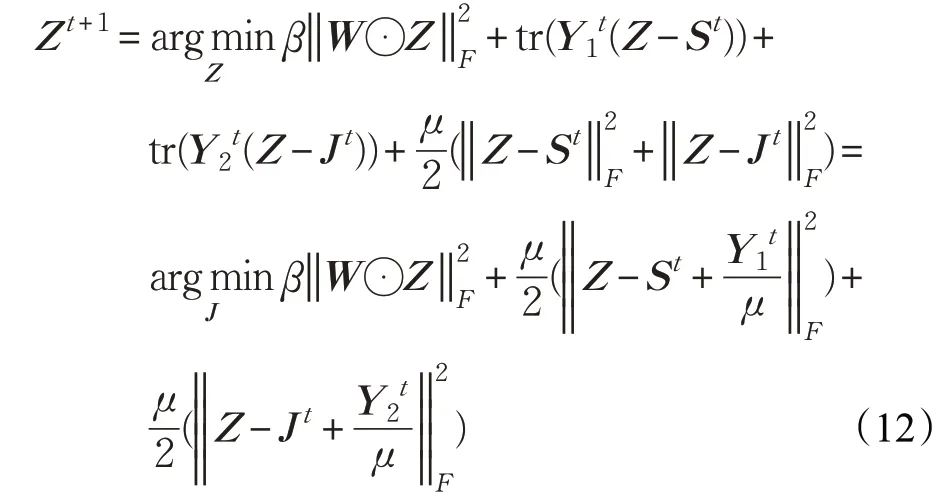
由上式可知Z有解析解：

更新J，固定Z,S：

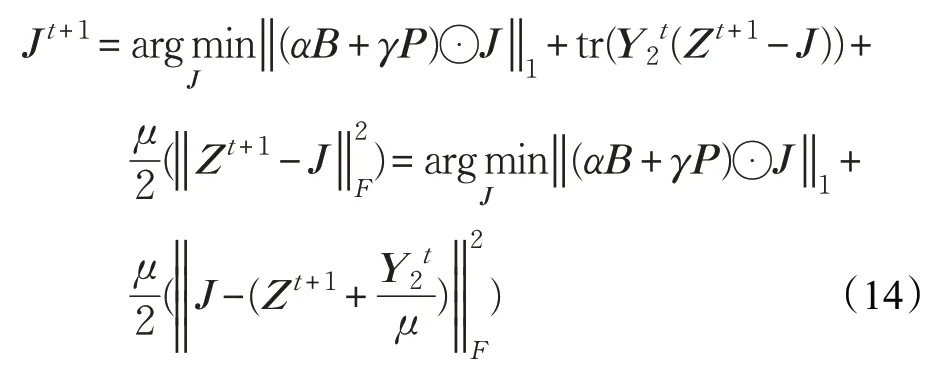
J可以通过软阈值算子得到：

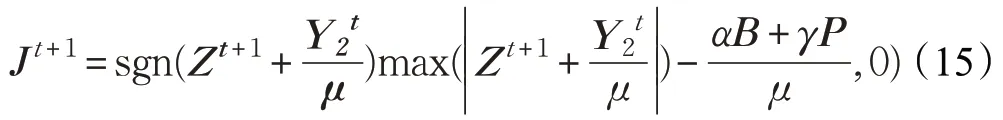
更新S，固定Z,J：

式（15）为凸优化问题，可以通过直接求导得到S的解：

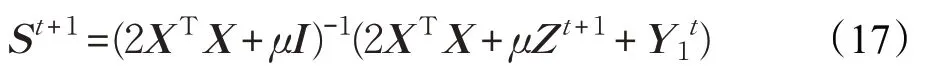
详细求解Z的步骤如下。

算法1 用ADMM解问题（6）

输入：数据矩阵X，模型参数α,β,γ。

初始条件：

输出：最优系数矩阵Z。

循环执行以下步骤：

1.固定其他，用式(13)更新Z；

2.固定其他，用式(15)更新J；

3.固定其他，用式(17)更新S；

4.更新拉格朗日乘子Y1,Y2,：

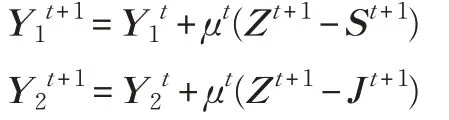
5.更新参数μ，μt+1=min(μmax,ρμt)。

6.迭代终止条件

7.t=t+1

结束

3.2.2 矩阵Q的求解

给定Q，问题（6）转化成以下形式：

因为：

因此上式变为：

由于式（19）非凸，因此松弛为：

最后，使用谱聚类算法将数据分组。

算法2 概述了SWCASC 模型的求解过程。子问题（1）求解过程是特征选择的过程，得到的系数矩阵Z作为特征向量进行聚类；子问题（2）是凸松弛问题，求解过程是谱聚类的过程。虽然上述两个子问题在理论上不能保证收敛，但是在实验中，当选取合适的参数时，算法收敛。

算法2 SWCASC模型求解

输入：数据矩阵X，参数α,β,γ。

输出：Q。

初始条件：P0=0

循环执行以下操作：

1.当给定Q时，通过算法1求解式（7）得到Z；

2.当给定Z时，通过谱聚类求解式（18）得到Q；

4 实验结果

本章展示了SWCASC模型在一些常用数据库上的聚类性能，包括Extended YaleB数据库[14]、MINIST数据库[15]、COIL20数据库[16]。将所提出的算法与现有的SSC、LRR、LSR、CASS、SSSC 方法进行比较，通过聚类精度acc=Nacc/Ntotal来评价所有方法的聚类性能。其中Nacc表示分类正确的数据样本的个数，Ntotal表示数据样本的总个数。图1给出了3个数据集的实验样本图。

在实验中，为了公平起见，上述所有方法的参数都选取聚类效果最好的那个值。并且每个数据库都进行20次实验，结果取平均值。SWCASC模型中有3个参数α、β、γ。在参数调整过程中，先给参数选取一定的范围，然后手动调整参数进行实验，观测聚类精度比较好的参数范围并记录下来。然后，固定两个参数调整第三个参数，使聚类效果达到最好，记录对应的参数值。以此类推，得到所有最优参数值。当γ=0.5 时，图2 显示了在Extended YaleB 数据集的前10 类上聚类精度随参数α和β的变化图。由于可看出当α=0.01,β=0.1 时，聚类精度最高。

图1 实验样本图

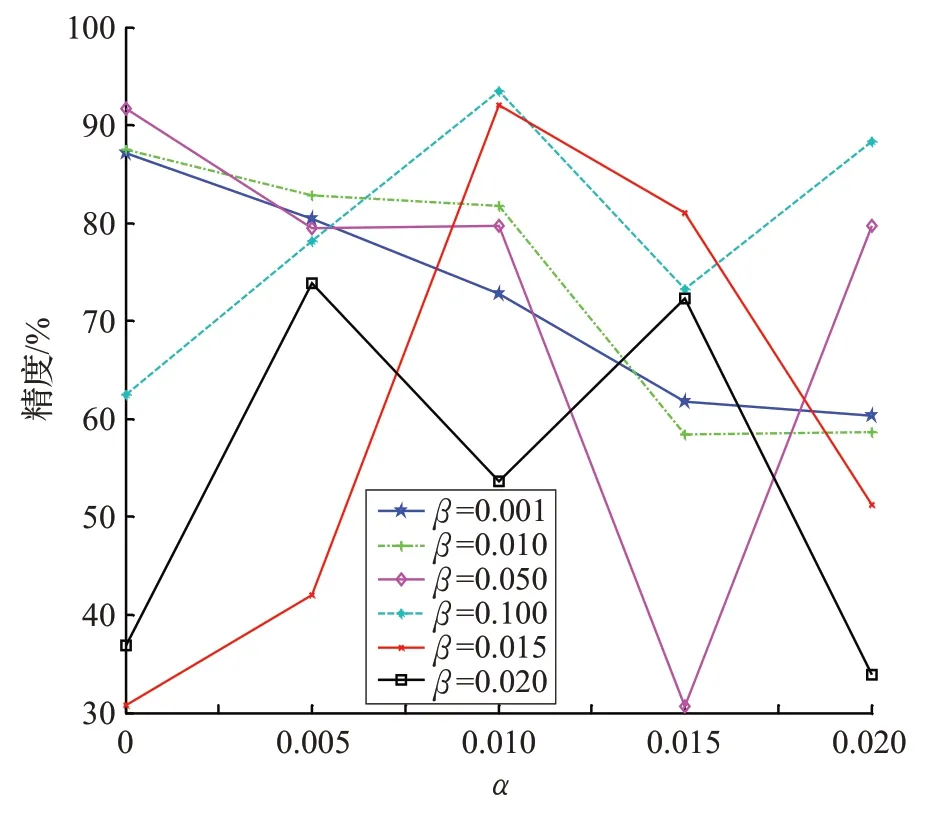
图2 在前10类上聚类精度随参数α 和β 的变化图

4.1 Extended Yale B数据集

Extended Yale B 是一个人脸数据集，由38 个在不同姿势和光照下的2 414 张正面人脸图像组成，每个人大约有64张正面人脸图像，每张图像有192×168个像素点。对于子空间聚类任务，每个对象对应一个子空间，每个子空间有64 个数据点。通过对该数据库的5 个、8个和10个人面部图像进行聚类，构建了3个子空间聚类任务。大量实验表明，当α=0.01,β=0.1,γ=0.5 时，聚类效果最好。

表1 给出在不同类别下，各种方法在Extended Yale B 数据集上的聚类精度的平均值、中值和标准差；图2 在Extended YaleB 数据集前10 类上聚类精度随参数α和β的变化图。

表1 Extended Yale B数据集的聚类精度 %

从表1 中可看出SWCASC 模型的平均聚类精度最高，表明SWCASC 模型比其他方法更好。为了更直观地比较各方法在Extended Yale B数据集上的聚类性能，图3 给出了各种方法在5 类、8 类和10 类上的聚类精曲线图。从图3 中可看出SWCASC 方法的聚类精度明显高度其他方法，而且随着类别的增加，其他方法的聚类精度下降很快，而SWCASC方法下降较为缓慢。

图3 各方法聚类精度随Extended YaleB数目增多的变化图

4.2 MINIST数据集

MINIST 是包含数字 0～9 的 10 类手写数字数据集，每个图像有28×28个像素，重新排列成784维向量，图1（b）给出了实验样本图。在实验中，选择数据库前50个样本进行实验然后投影成60 维向量，分析了分割精度。当α=0.1,β=10,γ=0.5 时，本文的方法聚类精度达到78.1%，明显高于其他方法的性能。表2 给出了各方法的聚类精度。

表2 MINIST数据集的聚类精度 %

4.3 COIL20数据集

COIL20 数据集由20 个物体在不同角度下的1 440张灰度图像构成，图1（c）给出了COIL20 数据集的部分样本图。实验中为了减少计算代价，每图伸缩为32×32后向量化为2 014 维向量，并用主成分分析（PCA）[16]降到60维。同时实验时只采用每个物体的前50张作为样本。大量实验结果表明，当α=0.01,β=0.1,γ=0.6 时，SWCASC聚类效果最好。表3给出了各方法在COIL20数据集上的聚类精度，由表可知，本文方法明显优于其他方法。

表3 COIL20数据集的聚类精度 %

5 结论

本文用数据点的相关系数对表示系数施加显式惩罚，采有1-范数和2-范数自适应加权，同时利用相似度与分割之间的关系，对表示系数矩阵采用结构范数，将子空间表示形式表述为结构加权相关自适应子空间聚类（SWCASC）问题。这种方法充分考虑了不相关数据的良好子空间选择能力和高度相关数据的分组能力，同时利用数据相似度与分割的依赖关系，使相似度矩阵同时具有类间稀疏性和类内一致性。实验结果表明，在常用数据集上，本文提出的方法优于其他的子空间聚类算法。