融合粒子滤波与蓝牙地标矫正的定位算法
2020-07-06郑晨辉张雨婷
郑晨辉,陈 璟 ,2,张雨婷,薛 伟
1.江南大学 物联网工程学院,江苏 无锡 214122
2.江南大学 物联网技术应用教育部工程研究中心,江苏 无锡 214122
1 引言
随着智能移动设备的普及,人们对于定位精度的要求也越来越高。在室外,GPS 可以获取精确的位置信息,但在室内,由于信号的遮挡,GPS 无法进行精确定位,所以在室内获取高精度定位结果具有很大的研究价值。
常见的室内定位技术有很多,但各自有缺陷,如红外技术[1],此方法定位效果好,但设备昂贵,且容易受到环境的影响。射频技术(RFID)[2],需要在定位空间中布置大量设备。WiFi[3]是室内定位中常用的方法,但是WiFi存在信号强度波动性大和功率高等特点,因此定位精度不高且耗能大。近几年,智能手机得到长足发展,内部传感器种类也越来越丰富,移动端的室内定位技术越来越受关注,常见的有利用传感器数据[4]结合PDR进行位置估计。PDR需要得到行人的初始位置,进而利用方向数据和步长数据进行迭代计算,得出用户的运动轨迹。由此可知,这种定位方法受信号传播的影响不大,对比之前的方法,PDR算法更具普适性,低成本,低复杂度等特点。
在PDR算法方面,文献[5]的研究内容有计步算法、运动步长估计[6]和运动方向估计[7]。文献[8]中结合陀螺仪和磁场传感器提出了基于智能手机的行人航位推算算法。由于它们均使用智能手机中的传感器来实现定位,且手机内置方向传感器的数据容易产生方向偏差,加之PDR 算法容易产生漂移误差等问题,一些研究团队将室内特殊区域[9](如拐角等地)设置为地标,但在真实场景中的定位精度一般只是房间级(5 m 左右)。Li等[9]利用iBeacon 所在位置设定为地标,通过iBeacon 地标来矫正路径,但常常出现过分矫正的情况。
基于以上PDR 容易产生方向误差的问题,本文在粒子滤波算法[10]中为方向属性添加方向角偏差。同时,利用iBeacon 作为地标(landmark),对产生的漂移误差进行矫正,若地标有反复矫正的现象产生,本文利用RSS(Received Signal Strength)设定进出地标矫正的阈值,使iBeacon地标能有效的矫正漂移误差。
2 总体框架
算法的整体框架如图1 所示,在定位前,本文进行数据采集与步长步数的测量,然后进入融合算法定位模块,该模块分为两个部分:(1)基于粒子滤波的定位算法,该阶段粒子滤波算法中的粒子加入方向角偏差弥补了PDR算法中容易产生方向误差的问题。在粒子滤波定位算法中,经历粒子初始化与预测,方向误差校正两个过程,从而对行人的位置进行估计。(2)条件地标矫正算法,为了能够控制行人航位推算中的漂移误差,在该阶段,本文利用iBeacon 作为地标对行人位置进一步矫正,并根据蓝牙信号强度添加进出地标的条件,防止地标过度矫正,最终配合融合算法持续估计行人位置。
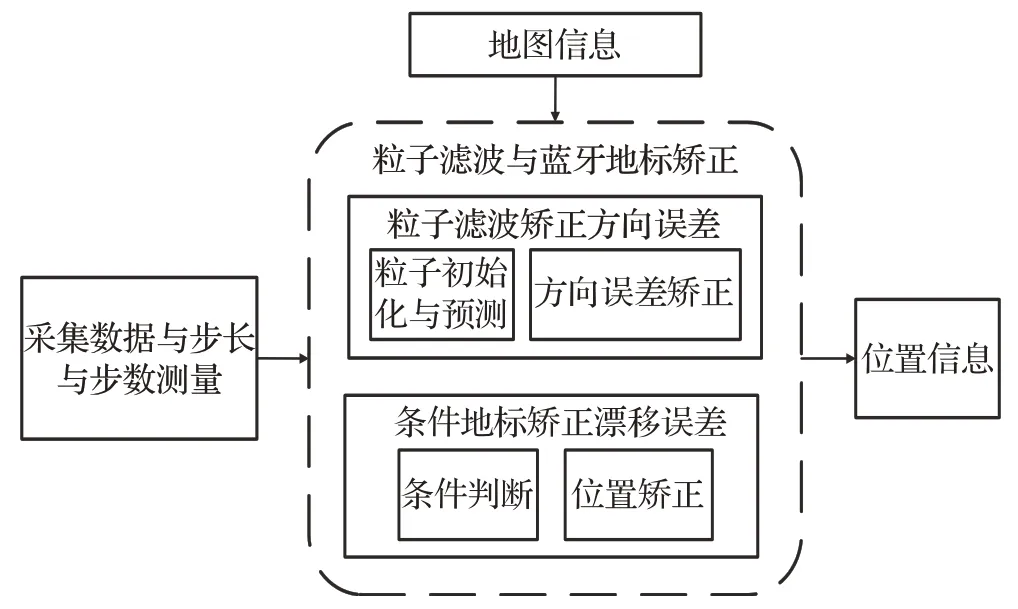
图1 算法的整体框架图
3 定位预备工作
智能手机内置传感器精度不高,采集到的数据带有大量噪声,本文在采集数据后,对蓝牙数据与加速度数据进行卡尔曼滤波[11]处理,如图2所示,经过处理过后的数据有效的抑制了噪声并且波形得到了平滑,既保留了原始的信号特征,又减少了信号的剧烈波动。

图2 经过卡尔曼滤波后的加速度与蓝牙数据
经过处理后的加速度数据被用来估计步数与步长,本文利用差分有限状态机[12](Finite-State Machine,FSM)估计步数,利用斯立卡特步长估计法[13]估计步长。
4 基于粒子滤波的方向校正
在本文的粒子滤波算法中,每个粒子将获得方向属性并添加方向角偏差,获取初始位置后进行粒子初始化,利用PDR 算法模型对每个粒子进行传播估计。在方向矫正阶段,首先结合室内地图数据进行权重更新,根据粒子的数量进行重采样,在重采样的过程中方向角偏差会被留存下来,对方向进行矫正,最后根据粒子状态和归一化结果进行位置估计,算法流程如图3所示。
4.1 粒子的初始化与粒子预测
在初始化模块中,首先在已知起始位置处产生粒子,并将粒子的权重设置为(N为粒子总数),同时获取运动方向,其中i表示粒子的编号,t表示时刻。

图3 粒子滤波算法流程图
在粒子的状态转移阶段,结合PDR 算法可以得到基本的状态转移方程如公式(1),其中L为行人步长,若检测到计步,每个粒子的状态发生改变且的状态都是根据该粒子的上一个状态而改变的。

4.2 方向误差矫正
方向矫正分为权重更新和重采样两个阶段,在粒子权重更新阶段,本文结合室内地图数据进行粒子的权重更新。如果粒子运动状态超出可活动范围(即粒子撞墙),粒子的权重将被置零。

置零代表着粒子已经消亡,此时粒子数量会有一定的减少,所以在权重更新后要对粒子的权重进行归一化处理,以便计算出用户位置。归一化处理如公式(3):

粒子撞墙消失会使粒子数量减少,影响定位精度和状态估计,因此该算法进入粒子重采样阶段。根据目前存在的粒子来生成新的有效粒子,所以当的值小于粒子总数的三分之二[14]时需要进行粒子重采样,如公式(4):

重采样阶段的主要目的是对粒子的方向属性进行计算,方向属性的表达如公式(5)所示,其中为粒子的方向属性,θt为传感器数据,θbias为实际方向与传感器方向之间的偏差,为服从零均值分布的高斯噪声。在粒子初始化过程中θbias为零,在重采样之后存留下来的粒子方向噪声会积累下来更新θbias。
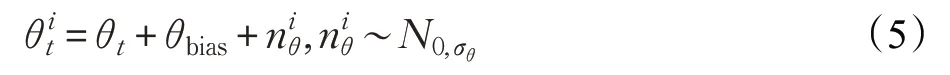
因此在每次重采样的时候都会把存活粒子中的方向噪声误差均值,保存到重采样后粒子的固定方向角偏差θbias上。其更新方程如公式(6)所示,其中,Ns表示存活的粒子数,ηθ是增益系数。一般情况下,因为方向上的噪声补偿是服从零均值的高斯分布,所以θbias的值会接近于零。如果运动方向与传感器方向产生一定角度误差时,方向噪声接近角度偏差的粒子会继续留存下来,其他粒子相继超出活动范围导致粒子消失,此时θbias的值将不会接近零。

经过以上两个阶段后,结合所有粒子状态和归一化结果可以计算出当前目标的位置信息,如公式(7):

从图4中可以看出,在粒子初始化阶段添加高斯噪声粒子间会产生一定的差异性,并且随着行人的不停运动,粒子发生了扩散,所以结合室内地图数据可以得到比较准确的方向。

图4 粒子滤波方向矫正示意图
由图5 可以看出当粒子数量大于300 时,定位误差和定位成功率趋于平稳,若粒子数量小于100时定位误差大且定位成功率较低,因此本文结合算法运行时间与定位误差将粒子数量设置为300。

图5 粒子数量对粒子滤波定位效果的影响
5 条件地标矫正
虽然粒子滤波对用户行走方向进行了矫正,但是在位置估计的时候依然会产生漂移误差,所以本文利用地标对行人位置进行矫正,地标一般在室内作为辅助定位的工具。矫正过程为(如图6所示):当行人走到地标区域时,该地标将会纠正之前一段路的累积误差。不过在实际情况中,蓝牙信号的波动导致对于识别范围没有一个清晰的界限,因此会出现还未到地标中心点或者已经离开地标中心点,地标将强制矫正的情况,从而产生一定的矫正误差,因此本文进一步利用iBeacon 的RSS 设定进出地标的条件,使iBeacon地标进行合理的矫正。
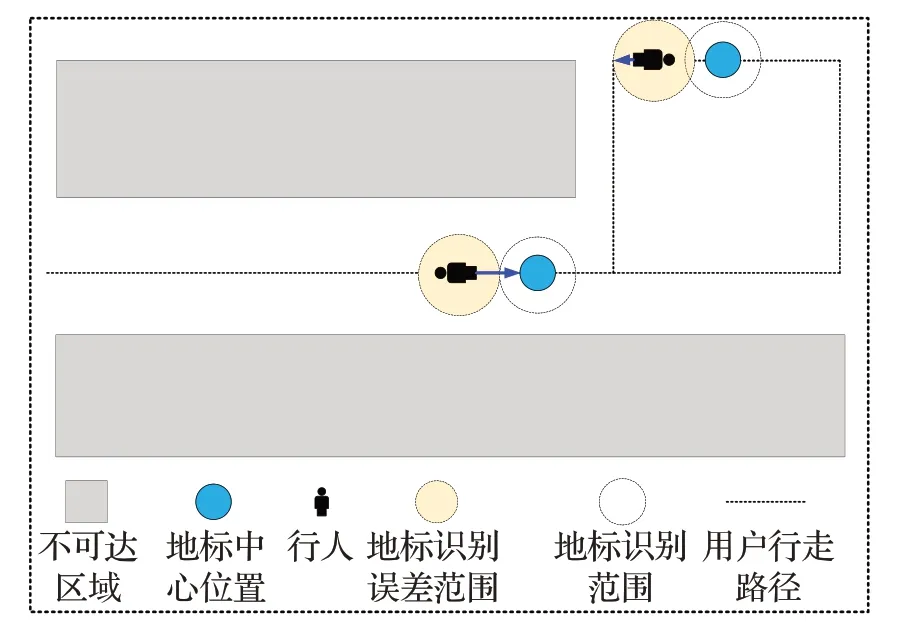
图6 地标矫正示意图
条件地标矫正的过程为:先对蓝牙信号进行卡尔曼滤波,通过多项式回归模型拟合出信号强度与用户之间的距离关系,从而设定出合理的进出地标的信号阈值,最后对行人位置进行矫正,流程框图如图7所示。
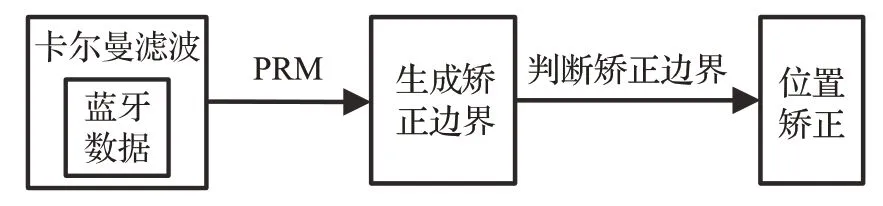
图7 条件地标矫正流程图
5.1 矫正条件生成
本文利用多项式回归模型[15](PRM)计算出矫正的恰当条件。对于信号传播模型而言,由于在室内环境中,蓝牙信号易受到遮挡,多径效应等的影响,因此信号传播模型不适合来估计信号与距离的关系。PRM模型将RSS 和距离的关系假设为一个n阶多项式,通过采集和训练蓝牙数据拟合出多项式参数,PRM 模型如公式(8):

其中ci是n阶多项式的系数,RSSi是蓝牙信号强度,dPRM表示对应的估计距离。此时多项式模型拟合误差平方和如公式(9):

其中M表示采样点个数,dj表示第j个采样点与iBeacon设备之间的真实际距离,表示第j个采样点处的RSS。本文利用最小二乘法求最优解,即求E的最小值,所以对公式(9)求偏导,如公式(10):

公式(10)可以简化成:

其中A矩阵内的元素为:(i的取值为 1 到n,B、C矩阵同理),B矩阵内的元素为:C矩阵内的元素为:ci,利用公式(11)求得多项式系数矩阵C,经过以上步骤可以得出多项式回归模型公式(12),另外,本文使用的iBeacon 都是统一品牌统一参数,所以仅需要一个PRM模型。

如图8 所示是使用多项式回归模型拟合出了RSS与距离间的关系图经过PRM 模型计算,将RSS 值转换成距离,得到iBeacon 的矫正条件:进入矫正范围的信号强度值−52 dBm,离开矫正范围的信号强度值−64 dBm。所以当用户走到iBeacon 附近时,蓝牙信号进入矫正范围之后,开始位置矫正,离开矫正范围时停止矫正。

图8 RSS与距离的关系图
5.2 位置矫正过程
输入数据为蓝牙数据(bluetooth)和方向传感器数据(orientation),输出数据为矫正后的位置。首先,算法遍历数据获取用户当前在哪一区域,即查找状态为IN的对应地标。若用户接收到来自对应iBeacon的RSS值小于−64 dBm,则表示用户已经离开矫正区域;若搜索到 iBeacon 的 RSS 值大于−52 dBm 且 iBeacon 的状态为OUT,此时进行位置矫正,修改对应iBeacon 的状态为IN,随即计算行人位置。如果用户此时继续在地标区域内,并不会触发该算法去矫正,而使用粒子滤波算法继续为用户提供位置估计,算法中进入地标区域的触发条件是RSS 大于−52 dBm。判断用户离开当前iBeacon的信号范围要选一个较小的RSS 值(本文选取的是−64 dBm),若RSS值较大,则导致该算法会频繁触发地标矫正,引起矫正误差,该算法的伪代码如下。
伪代码:条件地标矫正算法

6. iBeacon_in=which iBeacon state is IN
7. if state of iBeacon_in is IN and RSS of iBeacon<−64:
8. change the stateofiBeacon_in= OUT
9. iBeacon_max = which iBeacon has max RSS
10. if iBeacon_max is OUT and max RSS of iBeacon>−52:
11. distance=map max RSS of iBeacon to distance
12.X=iBeacon_max_postion_x-distance*sin(orientation)
13.Y=iBeacon_max_postion_y-distance*cos(orientation)
14. change the stateofiBeacon_max=IN
15. return positionX,Y
16. End Loop
由图9(a)可以看出,利用普通的地标矫正,会使位置结果聚集在地标附近,由于重复矫正所致;而从图9(b)可以看出,加入条件地标后的位置结果则不存在重复矫正的问题。
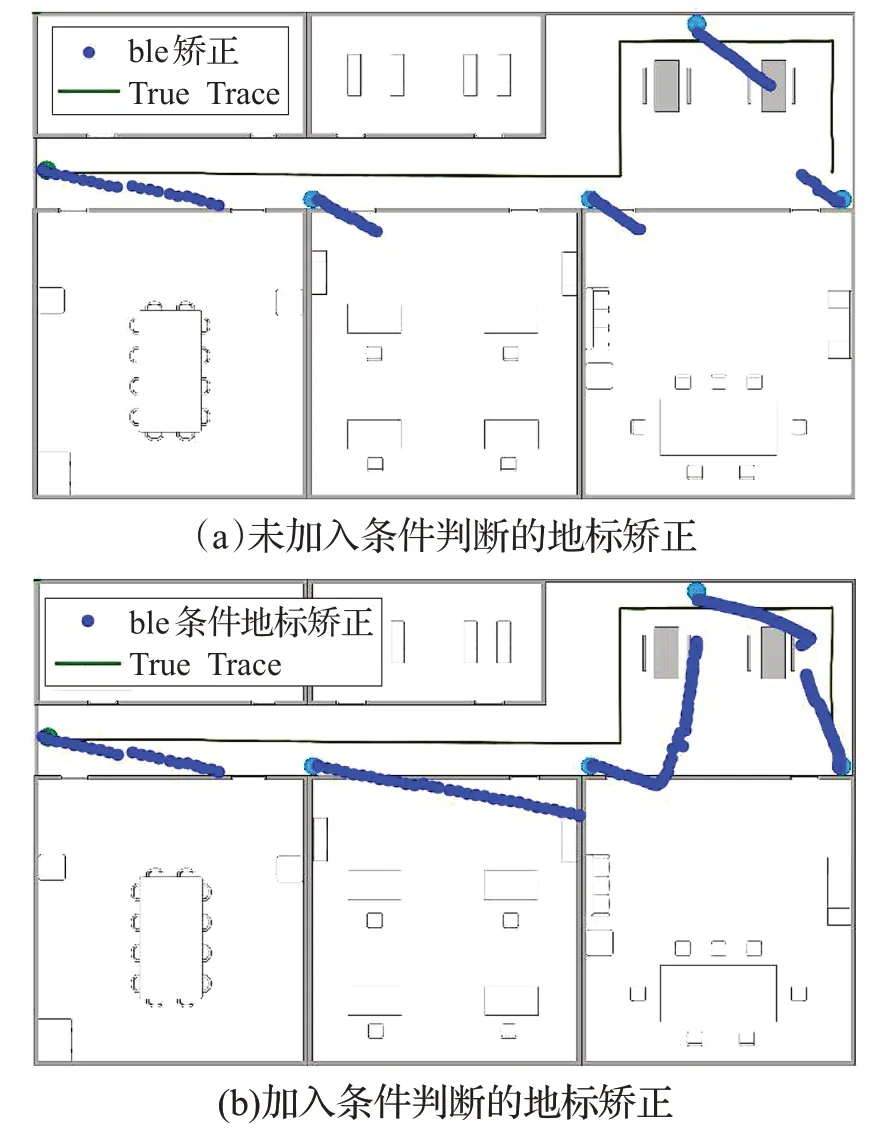
图9 普通地标矫正与条件地标矫正对比图
6 实验分析
6.1 实验环境及结果
本文的实验环境是学院B座的走道内,如图10(a),走道宽2.4 m(走道加休息区宽6.4 m),长30 m。绿色点为起点和终点,行走路线由西向东顺时针行走,最后回到起点,墙壁上的蓝色圆点是iBeacon设备的位置,为了不影响每个地标点的矫正,本文每10 m 布置1 个iBeacon 设备,在休息区的iBeacon 则布置到窗台中间,并将iBeacon 的发射频率设置为100 ms,发射功率设置为0 dBm。采集数据的设备是Vivox9plus手机。
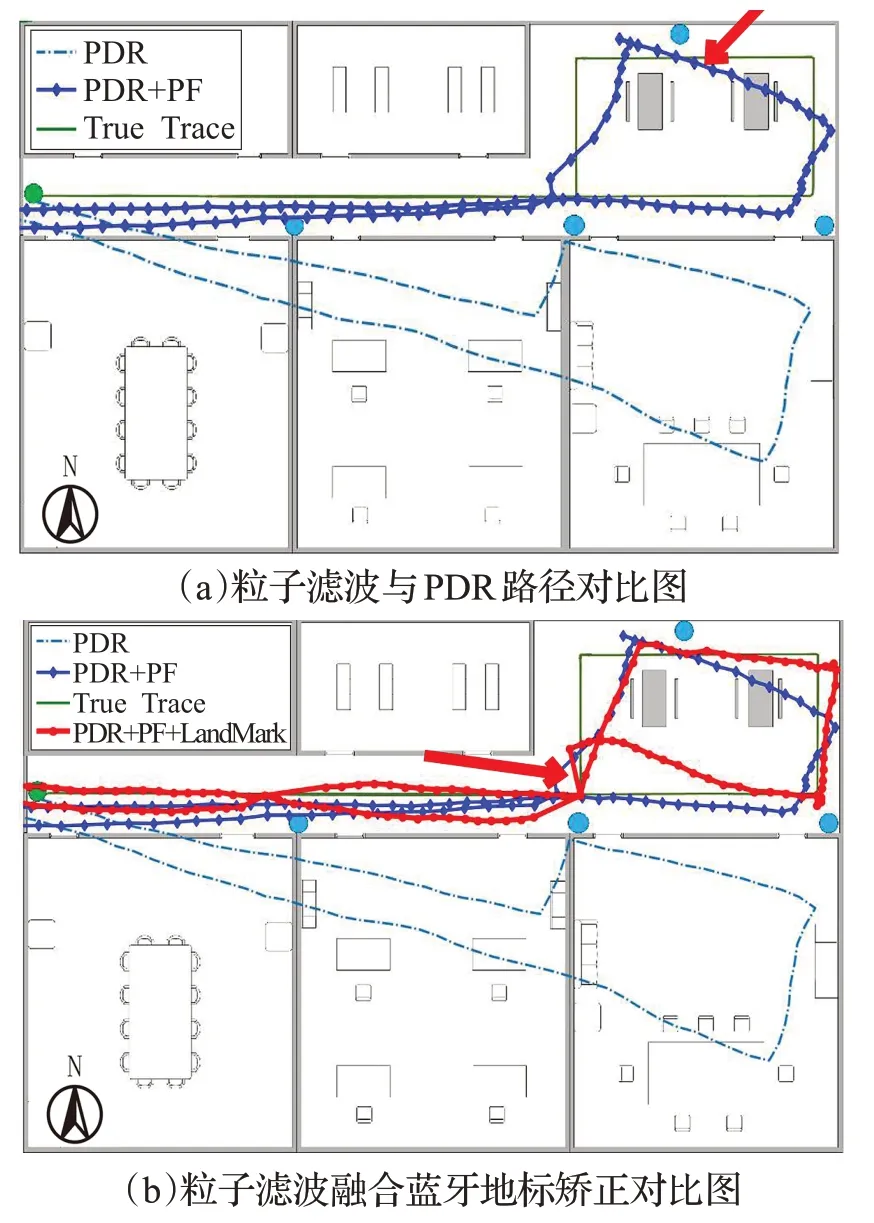
图10 实验环境及结果
由图10(a)可以看出,由于PDR算法在估计路径的时候无法及时矫正自身的方向误差,导致方向角误差越来越大,最后与真实路径相差甚远。因此,在粒子滤波算法中设置了方向角偏差,矫正了方向误差,由图10(a)中PDR+PF 路径可知,经过粒子滤波处理后的估计路径有了很大的改善,方向误差有了很好控制,但是在图10(a)中红色箭头处却有路径漂移,本文通过引入条件地标来进一步矫正行人位置。加入条件地标矫正后的估计路径得到了进一步的改善,如图10(b)中PDR+PF+LandMark路径所示,需要说明的是,条件地标矫正类似于信号的“拖拽”,所以形成了一个“拖拽轨迹”,将路径拉回到正常范围内,如图10(b)红色箭头处所示。
6.2 误差分析
由图11 可以看出,条件地标矫正可以在粒子滤波算法的基础上更有效地控制误差,粒子滤波与条件地标的融合算法的平均误差达到了1.05 m(如表1所示),且相对于PDR算法误差收敛更快,效果更好。
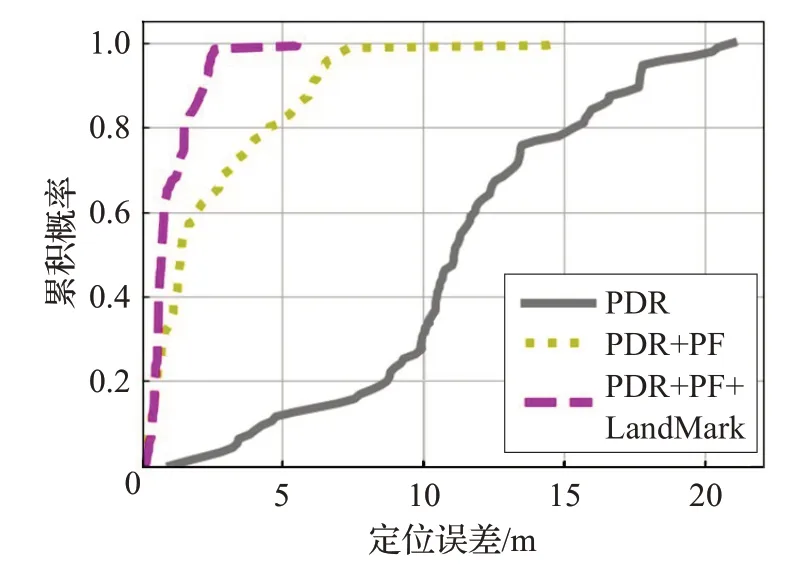
图11 三种算法的定位精度

表1 三种算法的定位误差m
7 结论及展望
本文使用粒子滤波算法对PDR算法中方向误差的矫正有较好的表现,同时,加入条件地标后一定程度上消除了行人路径的漂移误差,并且使地标矫正有了一定的合理性。通过实验分析,融合粒子滤波与条件地标矫正的平均定位误差达到1.05 m。
此外,本文使用的外部设备较少,iBeacon轻量方便价格低廉,智能手机普及率高。在未来的工作当中,本文将普适性进一步扩大,并将重点转移到多个房间穿梭,进出门的状态判断,尝试结合本文算法来估计上下楼的轨迹。
