流量控制继电反馈参数自整定研究
2020-07-06殷华文
殷华文
(南阳理工学院智能制造学院,河南 南阳 473004)
0 引言
Astrom和Hagglund在1984年提出基于继电反馈控制的比例积分微分(proportion integration differentiation,PID)参数整定方法[1]。基于继电反馈的PID参数整定过程完全在闭环条件下完成,对扰动不灵敏。另外,由于振荡幅度可控,因此其可广泛应用于大多数工业过程[2]。继电反馈PID参数自整定策略是在闭环控制方式下完成的,通过合理选择继电参数,过程被控参数能被保持在设定点附近[3]。
基于继电反馈测试的自整定PID控制策略一经提出,立即得到了广泛的关注。 通过一个标准继电反馈单元,就可以获取被控过程在临界频率点处的频率响应特性。但在控制器设计时,往往还需要了解其他一些频率点处的过程特性。为此,需要对标准继电反馈特性进行改进,例如在标准继电反馈环节后面串联一个积分或者微分环节,被控对象的相位被人为地超前或滞后了-0.5π;或者直接串联一个时滞环节,通过调整纯滞后时间来改变临界频率点。另一类改进的继电反馈方案是采用带有滞环的继电反馈[4-5]。本课题就采用这种反馈方法。
流量是典型的过程对象,具有惯性小、非线性的特点。如何在工作点附近产生稳定的振荡、提取振荡信息,则非常值得研究。本课题针对实际的流量对象,设计继电反馈参数自整定算法,实现对象的振荡和信息辨识;得到PID控制参数,实现对流量的控制。
1 流量控制回路设计
本课题以管道流量为被控变量,在继电反馈下观测流量的极限环振荡,并用Ziegler-Nichols公式计算控制器参数;参数整定完毕后,再投入PID控制。流量管道内径20 mm,供水压力50 kPa,调节阀为直行程电动调节阀,等百分比流量特性,流量变送器量程为0~1 200 L/h。控制系统中,控制器有两种模式可以选择,可根据开关的位置来确定控制器的工作状态。管道流量控制系统如图1所示。
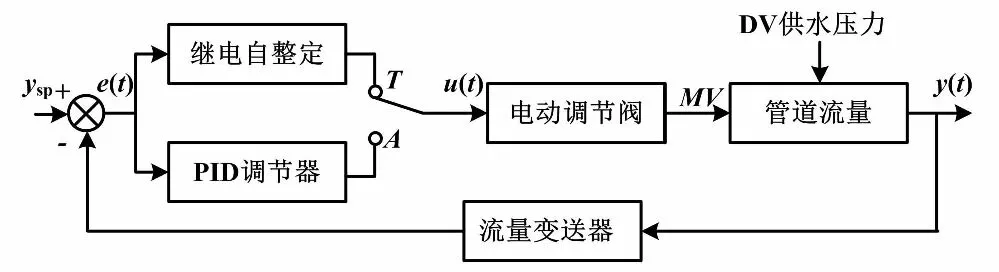
图1 管道流量控制系统框图
2 继电反馈的理论基础及参数整定思想
2.1 标准继电反馈
在控制系统中有两种状态:继电反馈控制状态和PID控制状态。在继电反馈控制状态下,利用继电控制的非线性特性使过程响应,出现极限环振荡测试系统的振荡频率和幅值,进而获得系统的频域信息或近似的模型结构;然后,由获得的系统信息根据选定的控制策略,求得控制器参数。在PID控制状态下,利用求得的控制器参数来运行系统。
在继电反馈控制下,被控对象只要具有至少-π的相位滞后,就可产生临界振荡。这样就可获得临界信息,然后应用Ziegler-Nichols公式确定PID参数[2]。
2.2 带滞环的继电反馈
为防止由于噪声产生的颤动,继电器应有滞环,同时反馈系统应使极限环振荡保持在规定的范围内。极限环法必须提供的唯一先验知识是继电器特性幅值d的初始值。继电器滞环的宽度h由测量噪声确定[6]。假设此时的临界增益为Ku,临界振荡周期为Tu。它们的计算如式(1)和式(2)[2]所示。
(1)
(2)
2.3 如何让广义对象振荡
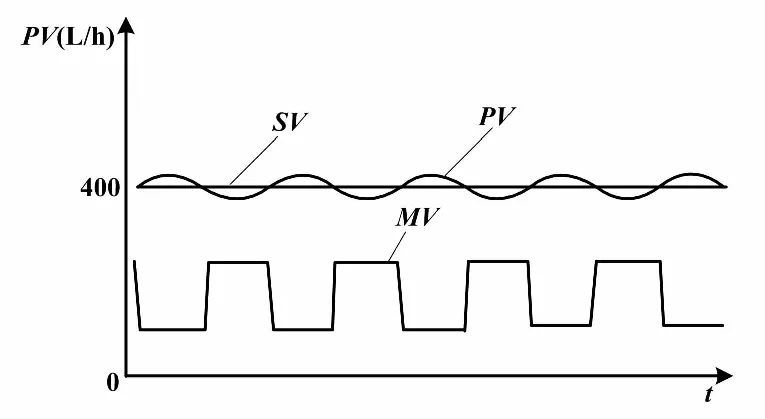
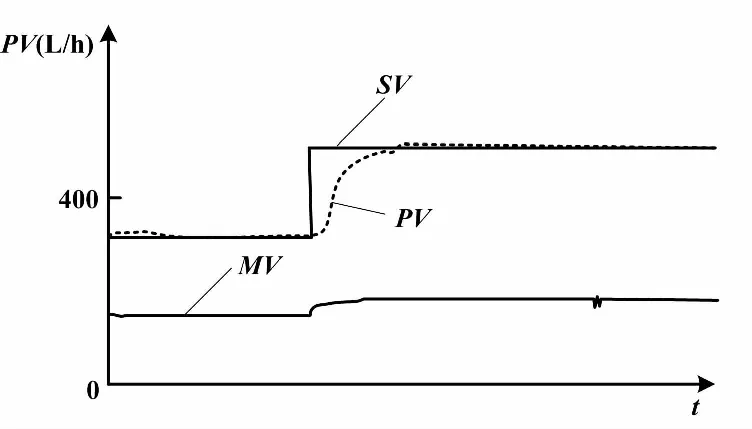
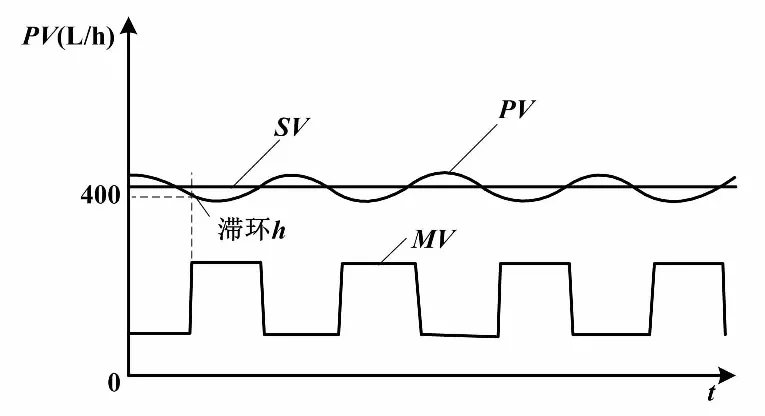
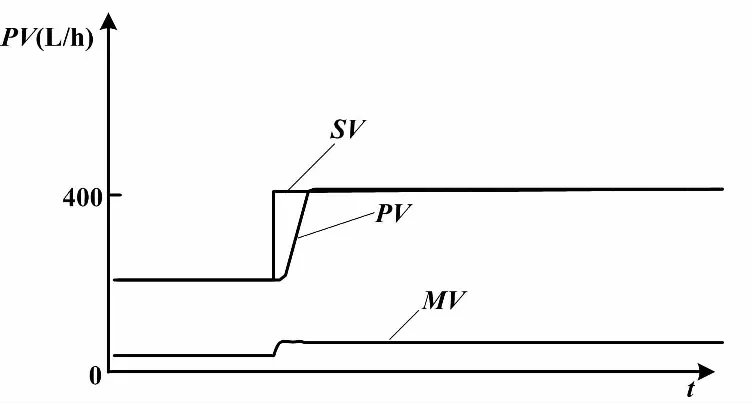
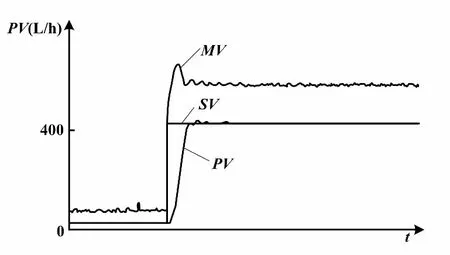
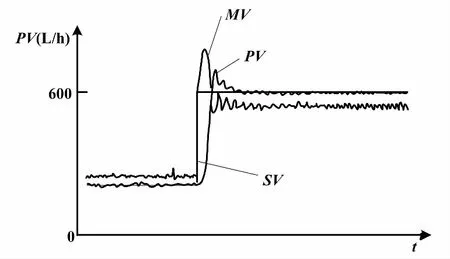
当继电环节对广义对象输出激励u=d时,被控变量(PV)开始增加。当PV>设定值(SV)时,继电环节的输出立刻翻转到相反的方向,u=-d。在u=-d激励下,输出PV开始减小。当PV 带有滞环的继电环节,因为存在滞环宽度h,所以当PV>SV且偏差绝对值大于h时,继电输出才会翻转变化。这使得继电环节的切换要延迟一段时间。临界振荡周期也会因此多出一段时间。振荡曲线的振幅a随之增加,临界增益则相应减小。带滞环的继电反馈振荡曲线原理如图2所示。 图2 带滞环的继电反馈振荡曲线原理图 图2中:d为继电输出高度;a为振荡的幅值;h为滞环宽度。 测出继电振荡周期Tu,根据式(1)可以反求出极限频率ωu。ωu反映了对象惯性的大小。测出振荡幅值a,根据式(2)可以计算出临界增益Ku。Ku可看作继电环节在传输幅度为a的正弦信号时的等价控制器增益。 Astrom的继电反馈试验是在继电环节输出u0=0的基础上,叠加一个幅度为±d的继电输出。但是对于实际执行机构来说,没有负位置,PID调节器输出为单极性0~100%。这样,继电输出应该在一个大于0的基值u0上叠加±d的继电输出,并且0 设继电特性输入一个正弦信号e(t)=asin(wt),则继电特性的输出u(t)是一个同相位、同频率、幅值为d的方波信号。将该方波信号作傅里叶级数展开,于是周期信号u(t)具有如下形式[7]: (3) 继电输出矩形波脉冲按照傅里叶级数分解,将会有许多谐波分量。基波是广义对象的固有频率波。继电输出脉冲的各个谐波分量经过广义对象后,就像经过一个选频器一样,只有和广义对象固有频率相应的谐波分量得以通过,而其他的谐波分量都将被衰减,最后就只剩下基波信号在系统内流动[8]。由于非线性环节无法用传递函数准确表达,所以用它传递的基波分量的幅相频率特性来描述。这就是描述函数[9]。广义对象既包括过程对象,又包括执行器和传感变送器。显然,广义对象的惯性有大有小。小惯性对象由于时间常数小,容易产生振荡;大惯性对象振荡起来比较困难。同样地,继电环节用在不同的广义对象的描述函数是不一样的。 继电反馈试验存在的误差主要是由两方面原因产生的。一方面是对继电非线性环节的近似估计,另一方面是被控对象的非线性。继电输出的方波可以近似为傅里叶变换的主谐波,并据此计算出相应的极限增益。被控对象的非线性会导致系统产生正负半周期的不对称振荡。对于不对称的振荡,振荡的幅值a可以取为振荡的平均值,从而减小误差,如式(4)所示[3]。 (4) 式中:amax和amin分别为振荡曲线的波峰值和波谷值。 即使出现了不对称振荡,由此求得的Ku和ωu仍然比较可靠。 采用阶跃响应法测试流量对象的数学模型。测试对象是除调节器外所有环节,因此测试所得的是管道流量对象的广义数学模型。考虑电动调节阀动作滞后因素,将管道流量对象近似为一阶惯性加纯滞后环节。对象数学模型可以选定为如下形式: (5) 调节阀开度从20%阶跃到40%时,测得T=3.89 s、τ=5.37 s、K=0.463。调节阀开度从40%阶跃到60%时,测得T=4.35 s、τ=5.45 s、K=0.59。调节阀开度从60%阶跃到80%时,测得T=4.11 s、τ=6.23 s、K=0.93。调节阀开度从80%阶跃到100%时,测得T=5.02 s、τ=5.23 s、K=2.33。 由以上数据可知,对应于调节阀不同的开度,放大增益K的差别很大。这是由于广义对象中存在着严重非线性。由于调节阀对象特性为对数特性,随着开度的变大,流量变化加快,放大增益K也变大。所以,流量对象为小惯性、非线性对象。 继电自整定控制器的主要任务是对继电反馈振荡曲线幅值a和周期Tu进行在线识别。在测得a后,可以求出临界增益Ku。最后,根据Ziegler-Nichols公式得到PID控制器的参数。计算临界增益Ku时要对变量参数作归一化处理,如式(6)所示。 (6) 式中:umax和umin分别为控制器输出的上限和下限;ymax和ymin分别为管道流量工作量程的上限和下限。 本设计中,继电输出为0~100%,流量的工作量程为0~1 200 L/h。 有了Ku和Tu后,就可以根据Ziegler-Nichols公式计算PID参数:P=0.6Ku,I=0.5Tu,D=0.12Tu。如果是改进型Ziegler-Nichols公式,则适度超调P参数为P=0.33Ku。 首先确定继电输出中心点u0和继电幅度d,然后启动参数自整定,并自动记录程序运行时间Tx。为了减少噪声,对测量值作数字滤波。 寻找工艺点:由于对象的非线性,所以继电振荡应在工艺工作点附近进行。使调节器处于继电自整定工作状态,并输出某一幅值u0。此幅值能使系统工艺参数达到工作点附近。在本课题的试验中,u0=60%。流量从0开始上升,当Tx累计到大约100 s时,流量在400 L/h附近稳定。将此时的流量值作为工艺流量,即流量设定值SV。 对象起振:当流量在工艺点达到稳定后,开始进行继电控制。如果PV>SV,u=55%,如果PV 振荡信息提取:设置变量C,用来记录实时流量PV曲线穿越设定流量SV线的次数。这样,C为半个振荡周期的个数。设置变量PVlast为上一次流量采样值。当PVlast 当C=9时,振荡曲线进入第五个周期,振荡曲线已比较稳定,记录此时时间T1。此时开始提取振荡信息。在流量上升过程中,通过递推比较找到流量波峰值amax。当C=10时,仍为第五个周期,记录此时时间T2。在流量下降过程中,通过递推比较找到流量波谷值amin。当C=11时,此时第五个周期结束,即将进入第六个周期,记录此时时间T3。按式(4)计算振荡幅值α。这样对于输出正负半周不对称的波形,计算结果仍较为可靠。根据T1、T2和T3,求取临界周期Tu,如式(7)所示。 Tu=(T2-T1)+ (T3-T2) (7) PID参数计算:根据Ziegler-Nichols公式或修正的Ziegler-Nichols公式计算PID控制器参数,并将自整定开关复位,结束继电反馈自整定过程,系统进入PID调节状态。 PID控制程序放在定时中断服务程序中,中断间隔500 ms,使PID按照一定的周期进行运算、输出。PID控制算式为改进型位置式PID算式,如式(8)所示。 (8) 式中:u(k)为对应执行机构的实际位置;y(k)和y(k-1)分别为本次和上次流量测量值。 PID算法采用的主要思想如下:梯形积分、微分先行[2]、偏差不灵敏区、积分保持等。为了实现从继电反馈振荡状态到PID调节状态的无扰动切换,需要把当前的继电反馈输出直接赋值给PID运算的积分初值。 采用理想继电反馈,继电输出u0=60%,继电幅度d=5%,滞环宽度h=0。按下“自整定”按钮,经过两个振荡周期就可以得到稳定的振荡波形。流量对象在理想继电反馈下的闭环响应曲线如图3所示。 图3 流量对象在理想继电反馈下的闭环响应曲线 由图3可知:振荡曲线波峰值为431.30 L/h,波谷值376.70 L/h,振幅a=27.3 L/h,临界增益为Ku=2.8,振荡周期Tu=14.00 s。振荡周期反映了对象惯性的大小,它将直接影响PID参数的计算。 由改进型Ziegler-Nichols公式整定适度超调下PID控制器参数为P=0.924、I=7.0 s、D=1.68 s。采用这一组参数对流量进行控制,适度超调下流量响应曲线如图4所示。 图4 适度超调下流量响应曲线 由监控曲线可知,自整定得到的PID参数控制效果比较满意。适度超调规则PID调节下,系统超调量为1%,稳态误差小于0.5%。 采用带滞环继电反馈,调节器继电输出u0=60%、d=5%、h=10 L/h。按下“自整定”按钮,其他步骤与理想继电整定试验相同,得到的流量对象在滞环继电反馈下的闭环响应曲线如图5所示。 图5 流量对象在滞环继电反馈下的闭环响应曲线 图5与图3相比,滞环继电的输入与输出不是相差180°,而是大于180°。这是因为流量曲线穿越稳态流量线时,继电输出不是立刻切换到相反方向,而是在稳态流量上下10 L/h的死区内继电输出不改变方向,大于滞环宽度时继电输出才切换到相反方向。滞环继电对存在强噪声的场合特别适用,可以避免执行机构在稳态值附近频繁切换。 由原始Ziegler-Nichols公式整定得到控制器参数P=1.515、I=8.001 s、D=1.920 s。滞环继电参数整定下,流量PID调节响应曲线如图6所示。 图6 滞环继电参数整定下流量PID调节响应曲线 由图6可知,系统有微量超调,但调节时间缩短。与理想继电相比,加入滞环后:振荡曲线临界周期Tu变大,由14 s变为16 s;临界增益Ku变小,由2.8变为2.525。但PID调节超调量变小,稳定性变好。 在流量控制系统中,设定值的调整是经常发生的。由于流量是小惯性对象,容易产生振荡,所以对微分比较敏感。因此,要求微分项对设定值的调整不起作用,以避免控制器输出大的跳变。这就需要在PID算法中加入微分先行运算。 使用带滞环继电反馈整定的PID参数,分别用标准PID和微分先行PID进行控制。图7是标准PID控制的响应曲线,图8是微分先行PID控制的响应曲线。 图7 标准PID算法响应曲线 图8 微分先行PID算法响应曲线 图7中,设定值阶跃变化时,调节器输出出现大的跳变。图8与图7相比,调节器输出跳变没有那么剧烈,反映了微分先行PID算法的优点。 前面的继电反馈振荡试验是在u0=60%,流量为400 L/h附近进行的。由于对象的非线性,因此整定出来的控制器参数在流量为400 L/h附近时控制效果较好,而在其他流量设定值时将不再是“最佳的”。一般用“鲁棒性”来描述控制器参数对对象特性变化的敏感性。使用图8参数,当设定值为600 L/h时的控制曲线如图9所示。图9与图8相比,系统超调量变大,稳态误差变大,控制效果变差。这是因为在高流量时,调节阀开度增大,增益Ku变大,控制通道放大增益也变大。在相同的PID参数调节下,系统呈现欠阻尼状态,所以超调量变大,稳定性变差。 设定值为600 L/h流量响应曲线如图9所示。 图9 设定值为600 L/h流量响应曲线 本课题对流量对象进行继电反馈振荡试验,通过对振荡曲线的在线自动辨识,实现PID控制器的参数自整定。由于对象的非线性,在不同的流量设定值下,参数鲁棒性较差,所以继电反馈振荡应在工艺点附近进行。继电反馈中心点u0的选择应能使对象工作在工艺点附近。由于对象惯性小,容易实现继电振荡,大部分情况下都能一次整定成功,所以带滞环的继电反馈参数整定结合微分先行PID算法适用于流量对象的控制。继电幅值d应选5%~10%,而滞环宽度h应大于流量信号的毛刺;在计算临界增益Ku时,须对变量参数作归一化处理。本课题研究的流量对象为小惯性对象。对于惯性大小不同的各种对象,如何实现继电幅值和滞环大小的自动寻找仍需作进一步研究。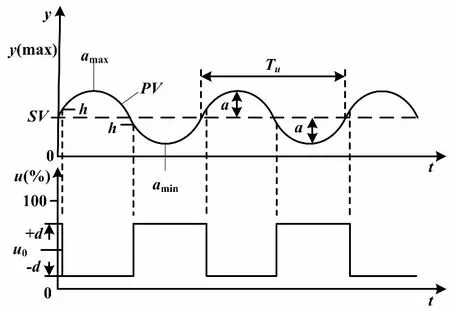
2.4 继电反馈振荡的物理意义
2.5 继电反馈试验误差分析
3 流量对象数学模型的测试
4 继电反馈自整定算法设计
5 继电反馈振荡方法设计
6 PID控制程序设计
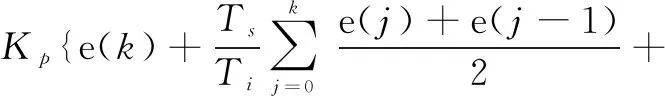
7 理想继电反馈参数整定试验
8 带滞环继电反馈参数整定试验
9 微分先行PID控制试验

10 控制参数鲁棒性分析
11 结论
