异形筒段吊具的设计与优化
2020-07-06
山西航天清华装备有限责任公司 山西长治 046000
1 设计背景
在航天产品总装生产线上,常常需要借助吊具来满足装配需求。对于形状规则的产品,吊具设计相对简单,有时采用车间吊带即可实现起吊。而对于异形筒段或者其它形状复杂的产品,设计一种专用的吊具显得尤为重要。
笔者以某型号产品异形筒段为适用对象,设计了一种新型吊具,并借助有限元分析软件,研究吊梁在最大起吊载荷下的结构强度和刚度,对吊梁进行拓扑优化,得到优化后的吊具结构。
2 吊具结构
应用Unigraphics软件建立了所设计的异形筒段吊具的三维模型,如图1所示。这一吊具主要由主吊梁、前吊梁、后吊梁、起吊组件、销轴、吊带、卸扣等组成。主吊梁和前、后吊梁之间采用螺栓连接,可以实现快速拆装,满足运输要求。吊装时,上端吊带直接与吊车吊钩连接,下端吊带通过起吊组件连接至异形筒段吊点上。
主吊梁由方钢管和起吊板焊接而成,并在方钢管两端焊接有法兰板,用于与前、后吊梁法兰板连接。在起吊板左右两侧各设计有四个直径为30 mm的孔,用于吊装时调节质心。
后吊梁主要由圆钢管折弯而成,且在折弯处焊接有斜圆钢管提高刚性。在圆钢管中部焊接有连接轴、法兰板,用于与主吊梁连接。后吊梁左右两腿底部焊接有堵板,堵板上开槽,并加工销孔安装销轴,通过吊带、起吊组件等与异形筒段吊点实现连接。前吊梁结构与后吊梁相似,为了使吊具自身质心和起吊时整体质心相重合,将后吊梁中的圆钢管换为圆钢,其余结构均相同。

图1 异形筒段吊具三维模型
吊梁作为整套吊具的关键部件,其结构直接关系到起吊安全和使用寿命,因此,有必要对吊梁进行有限元分析和优化设计。
3 有限元分析
为了验证异形筒段吊具的安全可靠性,笔者对吊具吊梁的受力情况进行有限元分析。将吊梁的三维模型导入ANSYS Workbench软件,对其进行网格划分,施加载荷和边界条件,最终得到有限元分析结果。
吊梁所用材料为Q345钢,屈服极限为345 MPa。主吊梁中方钢管尺寸为80 mm×80 mm×6 mm,前吊梁中圆钢直径为80 mm,斜圆钢直径为60 mm,后吊梁中圆钢管尺寸为φ80 mm×6 mm,斜圆钢管尺寸为φ60 mm×4 mm。吊梁总质量为407.2 kg。
主吊梁受力分析如图2所示。由于吊梁额定起吊质量为900 kg,因此Fz为9 000 N。前吊梁距离起吊点340 mm,后吊梁距离起吊点820 mm。Fq为前吊梁受力,Fh为后吊梁受力。起吊点即为异形筒段与吊梁的合质心位置。

图2 主吊梁受力分析
根据力矩平衡原理[1],有:
Fh×1 160=Fz×340
(1)
又有:
Fz=Fq+Fh
(2)
由此可得Fq为6 362 N,Fh为2 638 N。
可见,对于前吊梁而言,其受到竖直向上的合力为6 362 N,单侧受力为3 181 N;对于后吊梁而言,其受到竖直向上的合力为2 638 N,单侧受力为1 319 N。
由于异形筒段吊点的位置不同,实际使用时,前吊梁和后吊梁下端销轴的受力情况也不一样。吊梁力学三角形如图3所示。Fy1为前吊梁下端销轴处所受竖直方向的分力,Fx1为前吊梁下端销轴处所受水平方向的分力,F1为前吊梁下端销轴处所受合力,由此可知,前吊梁单侧销轴所受合力为3 290 N。Fy2为后吊梁下端销轴处所受竖直方向的分力,Fx2为后吊梁下端销轴处所受水平方向的分力,F2为后吊梁下端销轴处所受合力。由此可知,后吊梁单侧销轴所受合力为1 428 N。

图3 吊梁力学三角形
采用网格自动划分法,对吊梁模型进行网格划分[2-5]。吊梁网格划分结果如图4所示,节点数为141 154,单元数为77 892。

图4 吊梁网格划分结果
通过对吊梁施加相应的载荷和约束条件,求解得到吊梁的最大应力值为139.42 MPa,如图5所示,吊梁的最大变形量为4.36 mm,如图6所示。吊梁选用材料为Q345钢,屈服极限为345 MPa,安全因数为2.48,安全因数大,存在优化的空间。
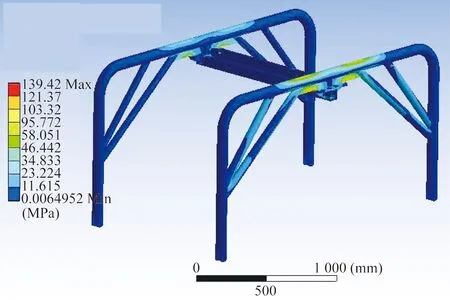
图5 吊梁应力云图

图6 吊梁变形云图
4 拓扑优化
为实现异形筒段吊具的轻量化设计,选择采用拓扑优化技术[6],对异形筒段吊具吊梁进行优化,既要使吊梁的整体结构强度满足要求,又要减轻质量。
进入ANSYS Workbench软件Shape Optimization模块进行优化设计,将轻量化目标设置为40%,得到吊梁的拓扑优化结果,如图7所示。
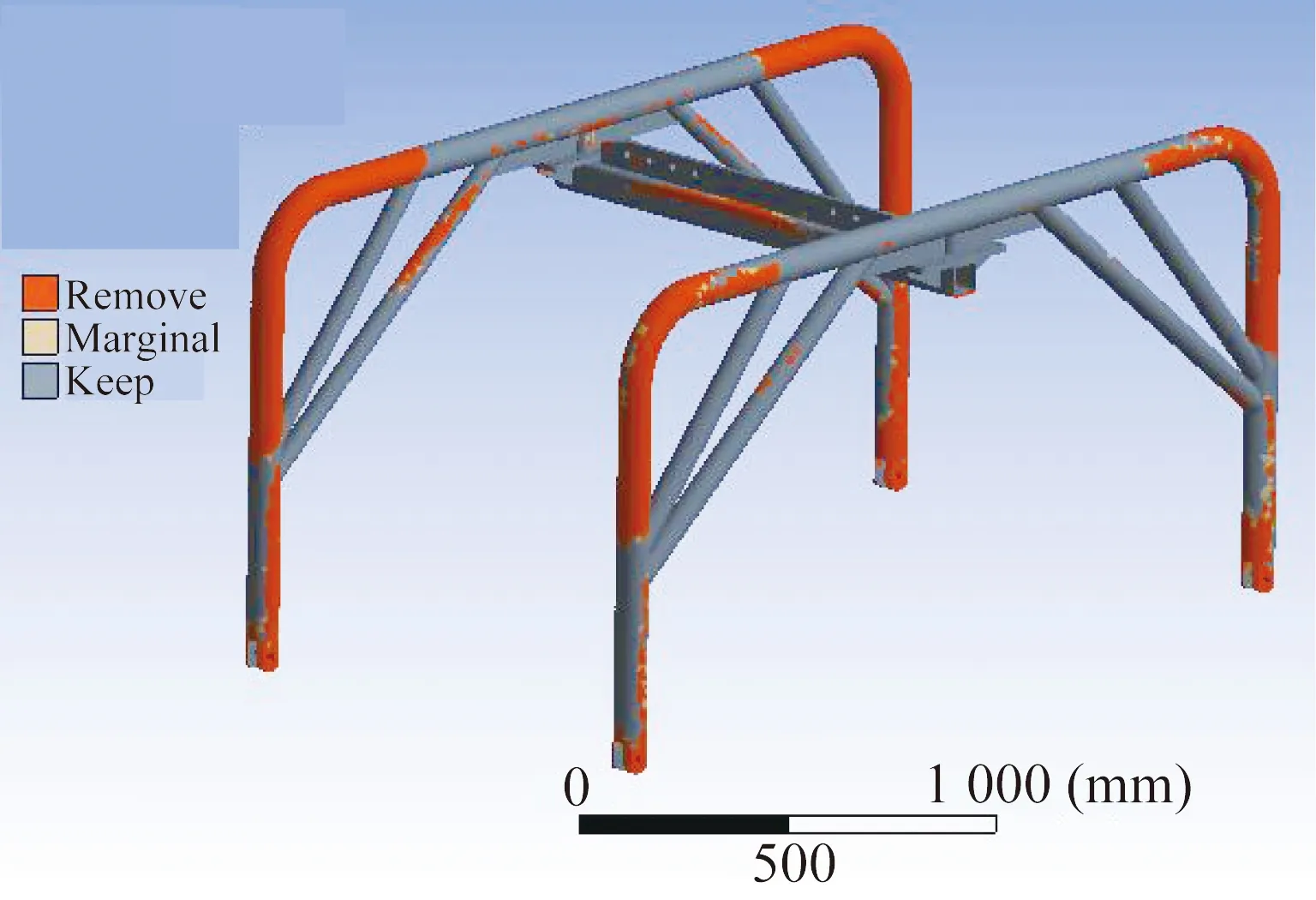
图7 吊梁拓扑优化结果
图7中,灰色区域为保留区域,红色区域为去除区域。可以看出,前、后吊梁的去除区域要远大于主吊梁的去除区域。因此,考虑将前、后吊梁所用材料的尺寸缩小,为实现整体比例协调,同时将主吊梁所用材料的尺寸也适当缩小。
依据优化结果,对吊梁三维模型进行修改。优化后吊梁模型如图8所示。优化后,主吊梁中方钢管尺寸为70 mm×70 mm×6 mm,前吊梁中圆钢直径为60 mm,斜圆钢直径为50 mm,后吊梁中圆钢管尺寸为φ60 mm×6 mm,斜圆钢管尺寸为φ50 mm×4 mm。此时,吊梁质量为238.3 kg。

图8 优化后吊梁模型
对优化后的吊梁模型进行网格划分,节点数为148 183,单元数为76 494,施加同样的载荷和边界条件后,再次进行有限元分析。优化后吊梁应力云图如图9所示,最大应力值为247.26 MPa。优化后变形云图如图10所示,最大变形量为11.9 mm。优化后安全因数为1.4,满足使用要求。
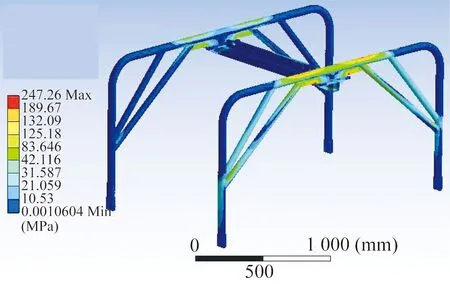
图9 优化后吊梁应力云图
5 结束语
笔者设计了一种易拆装、使用方便的异形筒段吊具,借助有限元分析软件,研究吊具吊梁在最大起吊载荷下的结构强度和刚度。为实现轻量化设计,对吊梁进行了拓扑优化,最终得到优化后的吊具结构。

图10 优化后吊梁变形云图
经分析,优化后的异形筒段吊具体积减小,质量减轻,结构强度依然满足使用要求。最终优化得到的异形筒段吊具,不仅外观美观,而且降低了生产成本[7-10],满足精益生产要求,符合未来吊具设计的发展趋势。
