一种优化的风格化边缘的生成方法

解婉誉，杨 明，李庆芹，徐 丹

(1.昆明冶金高等专科学校 a.人力资源处；b.通识与素质教育学院，云南 昆明 650033;2.云南财经大学信息学院，云南 昆明 650221；3. 云南大学信息学院，云南 昆明 650091)

0 引 言

非真实感绘制(Non-Photorealistic Rendering，NPR)[1]技术是计算机图形学领域正在蓬勃兴起的研究热点，目前在漫画[2]、水墨画[3]、铅笔画[4]、剪纸[5]等数字模拟方面均取得了丰硕的成果。非真实感绘制经常涉及到对边缘的模拟，常用的边缘提取方法有Sobel算子[6]、Canny算子[7]、风格化边缘[8]等。其中，风格化边缘效果最好，能够生成噪声较少、连续平滑的边缘，常用于各种非真实感绘制边缘的模拟。这些边缘提取方法都是对真实边缘的提取，不具备抽象化特征，因此，它们模拟不出具有刻制效果的边缘。

为了解决这一难题，本文提出了一种优化的风格化边缘的生成方法：它是对风格化边缘进行抽象化，具体是对边缘切线流ETF的平滑模型作出相应的改进，生成一种抽象线性风格的风格化边缘，此边缘能用于刻制边缘的模拟。

1 理论模型优化

1.1 风格化边缘的生成方法

风格化边缘的生成过程为：如图1所示，1)对源图像每个像素点进行Sobel算子边缘检测，得到每个像素点的边缘梯度向量；2)将梯度向量逆时针旋转90°，得到初始边缘向量，由所有像素点的初始边缘向量构成初始的边缘向量流场，这种流场的向量方向参差不齐，需要进行平滑处理；3)对初始边缘向量流使用迭代的ETF平滑模型平滑流场向量方向，即将每次平滑后的结果作为输入的流场进行下一次的平滑操作，多次平滑后得到平滑的边缘向量流场；4)结合源图像的灰度图和平滑后的边缘向量流场，使用迭代的各向异性的高斯函数差分DOG(Difference of Gaussian)[8]滤波器并二值化，最终得到风格化边缘。

本文对ETF的平滑模型作出了改进，促使了一种抽象风格的风格化边缘的生成。

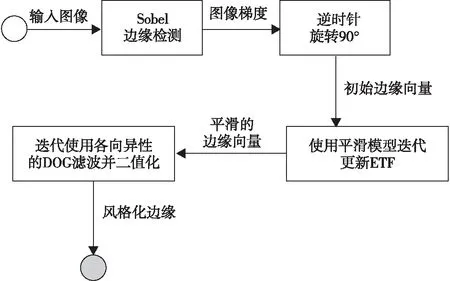
图1 风格化边缘的生成过程Fig.1 The generation process of stylized edges

1.2 优化的ETF平滑模型

1.2.1 原有的ETF平滑模型

公式(1)是原有的ETF平滑模型[8]：

(1)

其中，N(x)为当前中心像素x的邻域像素y所构成的集合；M是向量归一化因子；ei(z)代表像素点z当前的归一化切线向量；ei+1(z)表示像素点z平滑后的归一化切线向量；i为平滑次数。

W是单调递增的模值权重函数，如公式(2)所示：

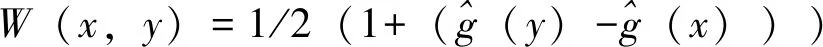
(2)

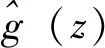
S(x,y)是邻域像素点边缘矢量的调向函数，它的定义是：

(3)

1.2.2 本文优化的ETF平滑模型

本文改进的ETF平滑模型在平滑次数较大时，能够生成具有局部线性特征的强边线性流，改进的模型如式(4)所示：

(4)

其中，ei(z)为像素点z当前的切线向量，并且不进行归一化处理；ei+1(z)是像素点z平滑后的切线向量，也不进行归一化。

W(x,y)=g(y)

(5)

其中，g(z)为像素点z不归一化的梯度模值，始终等于切向量模值。除此之外，本论文把M设为较大的常数，例如100。

新平滑模型的改进之处：

1)初始的边缘向量场与平滑后的边向量均不作归一化处理，简化步骤。

3)g(y)如果设置为定值即y点初始的梯度值，则新模型的平滑结果与原模型相同。为了生成更抽象化的效果，本文把g(y)的值跟随平滑后的边向量模值变化，以打破原有流场的形状，产生抽象的线性强边流场。另外，M设为较大常数，能够放大较大的边向量、缩小较小的边向量。因为在平滑公式(4)中，

例如：M=100，则公式为:

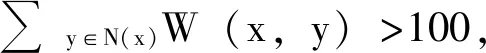
4)在迭代平滑过程中，新平滑模型每次平滑后的权重会变化，强边的权重值相对会越变越大，使平滑结果更大程度地趋向于强边方向，多次平滑将会把强边周围的方向均同化为强边方向，会失去原有的细节方向。而原模型的权重始终是由原图像边的强度决定，是定值，平滑后方向变化不大。

1.3 优化的风格化边缘

由风格化边缘生成的过程可以看出，经过优化的ETF平滑模型生成的抽象边缘流场，局部线性特征也会被由此生成的风格化边缘所继承，呈现出同样的强边线性特征，从而生成抽象风格的风格化边缘。

2 实验验证

2.1 优化的ETF模型实验结果

本文对优化的ETF模型用实验的方式验证理论的正确性。

验证中用到的线积分卷积 (Line Integral Convolution，简称LIC)[9]技术，是一种矢量场可视化技术，能够把流场可视化，用纹理的方式显示流场的形状(图2)。本文将使用线积分卷积技术验证优化的ETF平滑模型生成流场的抽象线性特征。

实验平台：visual studio 2008 ，编程语言：C++/C。

优化的ETF平滑模型的实验核心代码为：

for(int n=0;n

{

for(int i=0;i

{for(int j=0;j

{ if(i>0&&i0&&j

{

l0 = sqrt(vx0[i][j]*vx0[i][j]+vy0[i][j]*vy0[i][j]);

l1 = sqrt(vx0[i-1][j-1]*vx0[i-1][j-1]+vy0[i-1][j-1]*vy0[i-1][j-1]);

l2 = sqrt(vx0[i-1][j]*vx0[i-1][j]+vy0[i-1][j]*vy0[i-1][j]);

l3 = sqrt(vx0[i-1][j+1]*vx0[i-1][j+1]+vy0[i-1][j+1]*vy0[i-1][j+1]);

l4 = sqrt(vx0[i][j+1]*vx0[i][j+1]+vy0[i][j+1]*vy0[i][j+1]);

l5 = sqrt(vx0[i+1][j+1]*vx0[i+1][j+1]+vy0[i+1][j+1]*vy0[i+1][j+1]);

l6 = sqrt(vx0[i+1][j]*vx0[i+1][j]+vy0[i+1][j]*vy0[i+1][j]);

l7 = sqrt(vx0[i+1][j-1]*vx0[i+1][j-1]+vy0[i+1][j-1]*vy0[i+1][j-1]);

l8 = sqrt(vx0[i][j-1]*vx0[i][j-1]+vy0[i][j-1]*vy0[i][j-1]);//切向量模值就是梯度模值

if(vx0[i][j]*vx0[i-1][j-1]+vy0[i][j]*vy0[i-1][j-1]>0)

{ s1=1;}

else{s1=-1;}

if(vx0[i][j]*vx0[i-1][j]+vy0[i][j]*vy0[i-1][j]>0)

{ s2=1;}

else{s2=-1;}

if(vx0[i][j]*vx0[i-1][j+1]+vy0[i][j]*vy0[i-1][j+1]>0)

{ s3=1;}

else{s3=-1;}

if(vx0[i][j]*vx0[i][j+1]+vy0[i][j]*vy0[i][j+1]>0)

{ s4=1;}

else{s4=-1;}

if(vx0[i][j]*vx0[i+1][j+1]+vy0[i][j]*vy0[i+1][j+1]>0)

{ s5=1;}

else{s5=-1;}

if(vx0[i][j]*vx0[i+1][j]+vy0[i][j]*vy0[i+1][j]>0)

{ s6=1;}

else{s6=-1;}

if(vx0[i][j]*vx0[i+1][j-1]+vy0[i][j]*vy0[i+1][j-1]>0)

{ s7=1;}

else{s7=-1;}

if(vx0[i][j]*vx0[i][j-1]+vy0[i][j]*vy0[i][j-1]>0)

{ s8=1;}

else{s8=-1;}

M=100;

vx2[i][j]=(s1*vx0[i-1][j-1]*l1+s2*vx0[i-1][j]*l2+s3*vx0[i-1][j+1]*l3+s4*vx0[i][j+1]*l4+s5*vx0[i+1][j+1]*l5+s6*vx0[i+1][j]*l6+s7*vx0[i+1][j-1]*l7+s8*vx0[i][j-1]*l8)/M;

vy2[i][j]=(s1*vy0[i-1][j-1]*l1+s2*vy0[i-1][j]*l2+s3*vy0[i-1][j+1]*l3+s4*vy0[i][j+1]*l4+s5*vy0[i+1][j+1]*l5+s6*vy0[i+1][j]*l6+s7*vy0[i+1][j-1]*l7+s8*vy0[i][j-1]*l8)/M; }

}

}

for(int i=0;i

{for(int j=0;j

{ vx0[i][j] = vx2[i][j];

vy0[i][j] = vy2[i][j];}}

}

实验结果:如图3所示：(a)是源图像;(b)是一般的ETF模型所生成的流场的LIC结果图;(c)是优化的ETF模型所生成的抽象流场的LIC结果图。从实验结果对比中可以看出，(c)的流场具有局部线性特征，例如胡须、毛发表现出比较凸显的平直特性，这些特性说明了优化的ETF模型是能够生成抽象线性的流场。

图2 LIC方法Fig.2 LIC method

图3 传统的ETF与本论文优化的ETF的LIC对比实验图Fig.3 LIC comparison between the traditional ETF and the optimized ETF in this paper

2.2 优化的风格化边缘的实验结果

风格化边缘的实验核心代码为：

for (s = -T; s <= T; s++) {

x = d_x + vn0 * s;

y = d_y - vn1 * s;

if (x > (double)width1-1 || x < 0.0 || y > (double)height1-1 || y < 0.0)

continue;

x1 = round(x);if (x1 < 0) x1 = 0; if (x1 >width1-1) x1 = width1-1;

y1 = round(y);if (y1 < 0) y1 = 0; if (y1 > height1-1) y1 = height1-1;

val = licImage[x1][y1];

dd = ABS(s);

if (dd > W) weight1 = 0.0;

else weight1 = gauss(dd, sigmac);

sum1 += val * weight1;

w_sum1 += weight1;

weight2 = gauss(dd, sigmas);

sum2 += val * weight2;

w_sum2 += weight2; }

sum1 /= w_sum1;

sum2 /= w_sum2;

F[i][j] = sum1 - rol * sum2;///F即为DOG

对优化的风格化边缘进行实验，结果如图4所示。

图4 优化的风格化边缘实验结果对比图Fig.4 Comparison of optimized stylized edge experiment results

从图4可以看出，与传统的风格化边缘相比，经过优化的风格化边缘呈现局部线性平直特征，这种边缘由强边信息构成，离散点比较少，图像也较干净，是一种抽象特征的风格化边缘。

3 结 语

1) 可行性分析。本文提出优化的风格化边缘生成方法是对传统的风格化边缘进行改进，所生成的一种具有抽象线性特征的边缘，它是对ETF的平滑模型作出了相应的调整。经理论和实验验证，这种边缘是具有刻制特征的。

2) 应用前景。传统的边缘提取方法是真实边缘的反映，不具有抽象性；而本文优化的风格化边缘具有抽象线性特征，由强边信息构成，线条简洁、离散点较少。这些优点决定着它可以应用于一些刻制特征的风格化绘制的模拟，例如壁刻、木刻版画、雕刻等。凡是刻制作品的边缘都需要经过一刀一刀地刻制，线条不会很圆滑地过渡，并且只反映主要的信息，本文优化的风格化边缘很适合这类刻制的模拟。

本文使用优化的风格化边缘对壁刻作了实验模拟，实验结果如图5所示：(a)是源图像，(b)是传统的风格化边缘模拟壁刻的效果，(c)是优化的风格化边缘模拟壁刻的效果。从(b)、(c)的效果对比中可以看出，本文提出的优化的风格化边缘模拟壁刻的效果较好，产生的噪声点更少，线条风格趋向于笔直抽象，更适宜模拟刻制的边缘。

图5 模拟壁刻的对比图Fig.5 Comparison of simulated wall carvings