滤棒压降宏观模型的建立及应用
2020-07-05袁功道谢建伟
袁功道,谢建伟
( 珠海醋酸纤维有限公司,广东 珠海519050 )
0 前言
在滤棒成型过程中,时常发生压降稳定性波动大,停止生产进行试验改进需要耗费大量精力和时间,继续生产质量又难以保障,使生产陷入两难的境地。 因此许多工程师利用DOE进行大量试验和分析,以求分析出成型加工过程中各工艺参数对质量的影响。 高明奇[1]采用“单因素试验” 的研究方法,研究了螺纹辊压力、辊速比、稳定辊压力等工艺参数对丝束开松稳定性的影响。 赵红霞[2]运用DOE 试验设计等现代统计技术,对KDF-2 成型机主要设备参数与滤棒关键质量指标的关系进行了综合分析,用综合平衡法得出综合质量的最优参数组合。罗光杰[3]利用正交试验研究了辊速比、辊压力、空气喷嘴压力、稳定辊压力等滤棒成型工艺参数对滤棒压降稳定性的影响,研究形成了一套规范系统的“ 滤棒压降动态调整方法”。
通过DOE 试验能取得一定效果,但是DOE需要较强能力的试验团队,同时也需要充足的物资和时间,在客户需求紧急的情况下很难顺利展开。 通过对大量理论的分析和实践的总结,建立一般情况下的滤棒压降宏观模型,并且结合实际分析模型的影响因素,在生产中根据实际情况对应模型,从而快速找到解决思路,可以大量节省资源和时间。
1 材料与方法
1.1 材料及设备仪器
二醋酸纤维素丝束、KDF-2 滤棒成型机(许昌烟草机械有限公司)、综合测试仪(CERULEAN)。
1.2 方法
运用物理学宏观模型的方法,建立标准棒模型、横向分布不均模型、纵向分布不均模型。生产过程中,行车运行速度设置为200 m/min,设备运行稳定后,确保成型滤棒压降稳定在标准 范 围 内 (每30 支 均 值:(300 ± 10)mm H2O)、圆周稳定在标准范围内 (每30 支均值:(19.8 ± 0.05)mm),待设备稳定运行5 min后,每隔2 min 取样一次,每次30 支,共取5组。 将试验样品置于恒温恒湿控制室 (温度:(22 ± 2)℃,相对湿度:60% ± 3%)平衡2 h后进行测试,用CERULEAN 综合测试仪进行测量。
2 滤棒宏观模型的建立
2.1 标准棒模型
当滤棒的规格确定,填充量和圆周成了决定滤棒质量的关键因素。 要想获得质量稳定的滤棒,成型滤棒中开松丝束的分布必须满足:①横向分布均匀; ②纵向分布均匀。 如图1 所示,丝束在滤棒中横向、纵向分布均为均匀状态,即滤棒纵向切面密度处处相等。

图1标准棒模型
2.2 横向分布不均模型
如图2 所示,滤棒横向分布不均主要分左侧密度不均型、右侧密度不均型、中间密度不均型、横向间断密度不均型四种类型,与标准棒相比,每一种情况都会导致滤棒重量和压降的波动,进而影响滤棒质量的稳定性。

图2 横向分布不均模型
2.3 纵向分布不均模型
如图3 所示,滤棒纵向分布不均主要分上侧密度不均型、下侧密度不均型、中间密度不均型、纵向间断密度不均型四种类型,与标准棒相比,每一种情况同样都会导致滤棒重量和压降的波动,进而影响滤棒质量的稳定性。

图3 纵向分布不均模型
3 模型影响因素的分析
3.1 分布不均模型影响因素分析
滤棒横向分布不均通常有如图2 所示四种情况,从开松的角度来看,主要是由于在成型过程中,丝束的横向开松效果不好,丝束在横向上出现过去卷曲或去卷曲不足,导致纵向切面出现密度不均。 大量的研究表明,丝束纵向切面密度不均除了与丝束卷曲过程控制不佳有关,还与开松过程中稳定辊压力、螺纹辊压力、辊速比有很大关系。
3.1.1 稳定辊的影响
稳定辊对丝束的开松效果影响重大。 随着稳定辊压力的增大,丝束所受的压力增大,输入辊对丝束的拉力增大,丝束的去卷曲作用增大,在其他工艺参数不变的情况下,滤棒的重量呈明显的下降趋势。 反之,当稳定辊压力逐渐减小,丝束的去卷曲作用变小,滤棒的重量呈明显上升的趋势。 因此稳定辊压力的变化会明显影响丝束的开松效果和滤棒重量的大小,进而影响滤棒压降的大小和稳定性。

图4 成型机结构简图
因此,在实际操作中,在同一种规格滤棒成型过程中,在加工工艺参数不变的情况下,如果发现某一批次滤棒的重量或压降波动较正常情况下明显变大,而且其波动并不呈现明显的对称性,说明此批次的滤棒可能存在横向分布不均的现象,此时可以尝试调节稳定辊来达到调控重量和压降大小的目的。
3.1.2 螺纹辊压力的影响
螺纹辊的压力同样会影响到丝束的去卷曲效果,其与稳定辊一起作用,对丝束进行拉伸去卷曲,以达到丝束横向开松的效果。 但是当螺纹辊压力过大时,不断会造成断丝,而且还会损伤螺纹辊本身。 螺纹辊压力过小,又会造成去卷曲效果不明显,造成丝束横向分布不均。因此,在生产中螺纹辊压力一般控制在适中位置。
3.1.3 辊速比的影响
辊速比为扩展辊速度与输入辊速度的比值。调节辊速比,不仅影响丝束横向开松效果,由于对辊上有螺纹,辊速比的变化也明显影响着丝束纵向扩展情况。 当辊速比增大时,丝束的横向拉伸作用和纵向开松效果增大,有利于丝束的横向去卷曲和纵向扩展。 当辊速比减小时,丝束的横向拉伸和纵向扩展表现都不明显。 因此在实际生产中,辊速比通常根据丝束的规格控制在合适范围。 同时,辊速比的调节通常与稳定辊同步,以求达到最佳效果。
3.1.4 喷嘴压力的影响
喷嘴是开松后丝束进入烟枪上胶定型的最后一道工序,因此丝束通过喷嘴后的形态直接影响到滤棒成型的效果。 通过调节喷嘴压力的大小,可以控制开松后丝束经过喷嘴后的收缩状态。 大量的研究结果表明,喷嘴压力应根据丝束规格选择合适的区间,并且在区间内越小越好。 如图3 所示,当喷嘴压力过大或过小时,很容易导致丝束定型时偏向一边,产生纵向分布不均的结果,进而影响滤棒质量的稳定性。因此,在实际生产中,可以通过观察丝束在喷嘴口的分布形态,从而判断是否需要调节喷嘴压力。 当发现喷嘴口有明显的飘丝现象时,说明喷嘴压力过小,不能很好的收紧丝束,应该适当增大喷嘴压力。 当喷嘴入口丝束过于聚集,出口丝束过于膨胀,此时应当减小喷嘴压力。
4 滤棒宏观模型在成型加工过程的应用
结合上述滤棒压降宏观模型和影响因素影响的分析,对一批质量偏离正常范围的滤棒进行优化试验指导。 如表1 所示,在生产过程中,收集、统计了一批质量波动较大的丝束所制滤棒的数据,滤棒重量和压降各收集5 组,每组30 支,共计150 支。
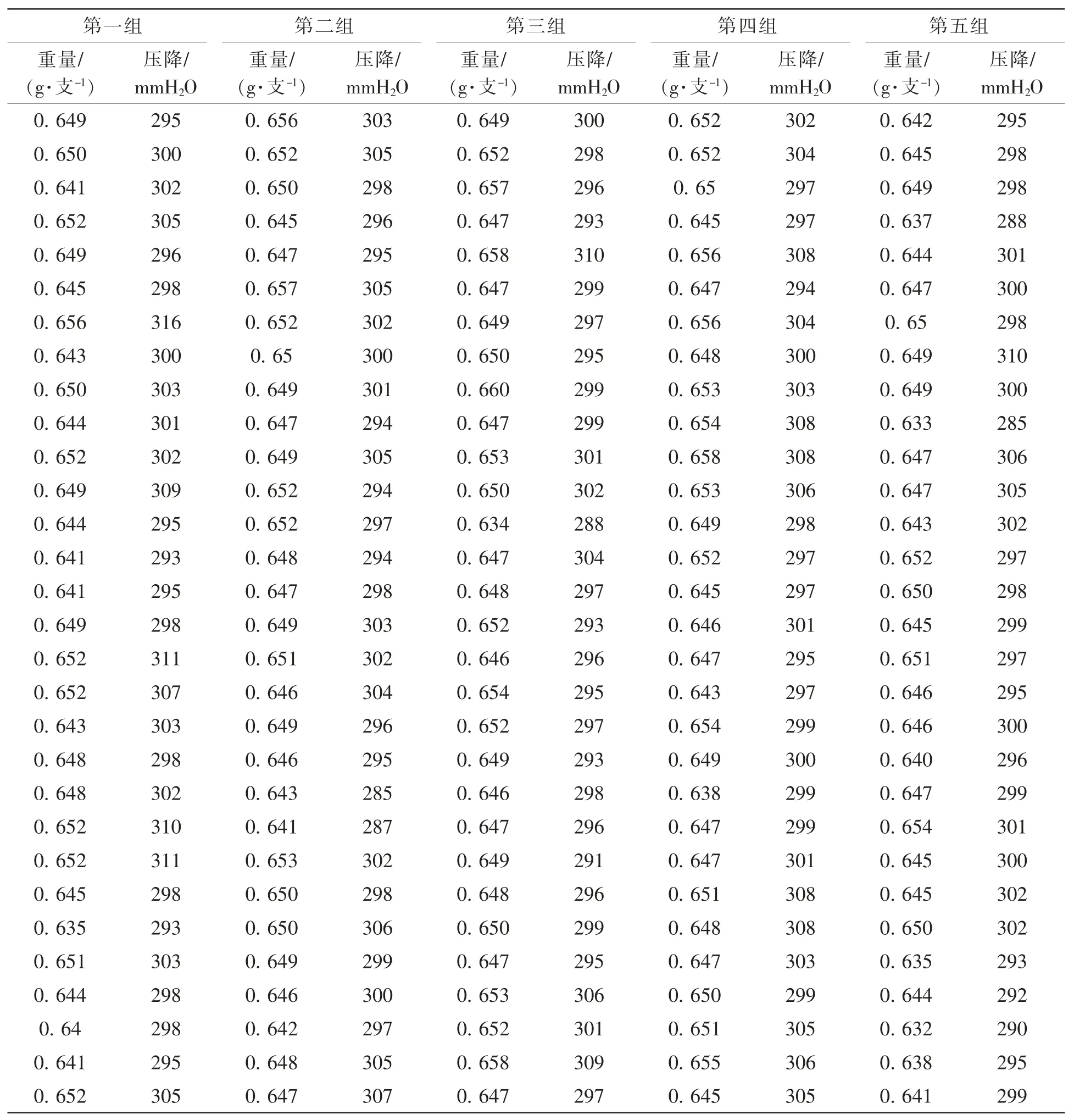
表1 优化前数据统计表
通过表2 可以看出,优化前150 支滤棒的重量均值为0.638 g,压降均值为299.4 mmH2O,极差达到53,压降STD 为10.85,与正常情况相比 (压降STD 小于7),该批次滤棒波动性较大。

表2 优化前基本统计表
正常情况下,该规格滤棒单棒重量一般为0.65 g 左右,压降为300 mmH2O 左右,通过图5 优化前重量和压降的直方图可以看出,此批次滤棒的重量中心值发生了明显的左移,压降均值正常。

图5 优化前重量和压降的直方图 (包含正态分散曲线)
结合重量、压降的单值图,如图6 所示,重量和压降的单值图均呈扁平的 “梭子” 状,并不向中心高度聚集,说明重量和压降的稳定性较差。 参考正常情况下的统计值,丝束制得的滤棒,一般重量范围为:中心值± 0.01 g,R 值小于0.02 g,压降范围为:中心值± 10 mmH2O,R 值小于20 mmH2O,此时滤棒重量和压降的稳定性较好。 通过计数统计,发现重量在低于0.628 g (控制规格下限)的点数明显多于0.648 g (控制规格上限)以上的点数,压降低于290 mmH2O (控制规格下限)以下的点数明显多于310 mmH2O (控制规格上限)以上的点数,说明此批滤棒重量和压降关于中心点均不对称,且超控制下限的异常点明显多于超控制上限。
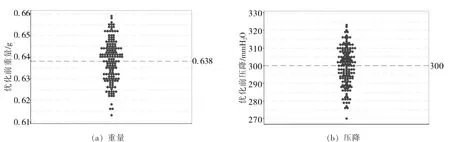
图6 优化前重量和压降的单直图
结合上面的结论,与正常情况对比,我们可以判断此批滤棒重量的中心值偏移,并且重量和压降超控制下限的异常点明显多于超控制上限。 根据滤棒宏观模型,可以推断此批次滤棒为横向分布不均型,具体为横向过开松不均型。 针对此类问题的解决办法为:适当减小稳定辊压力,适当增大辊速比。
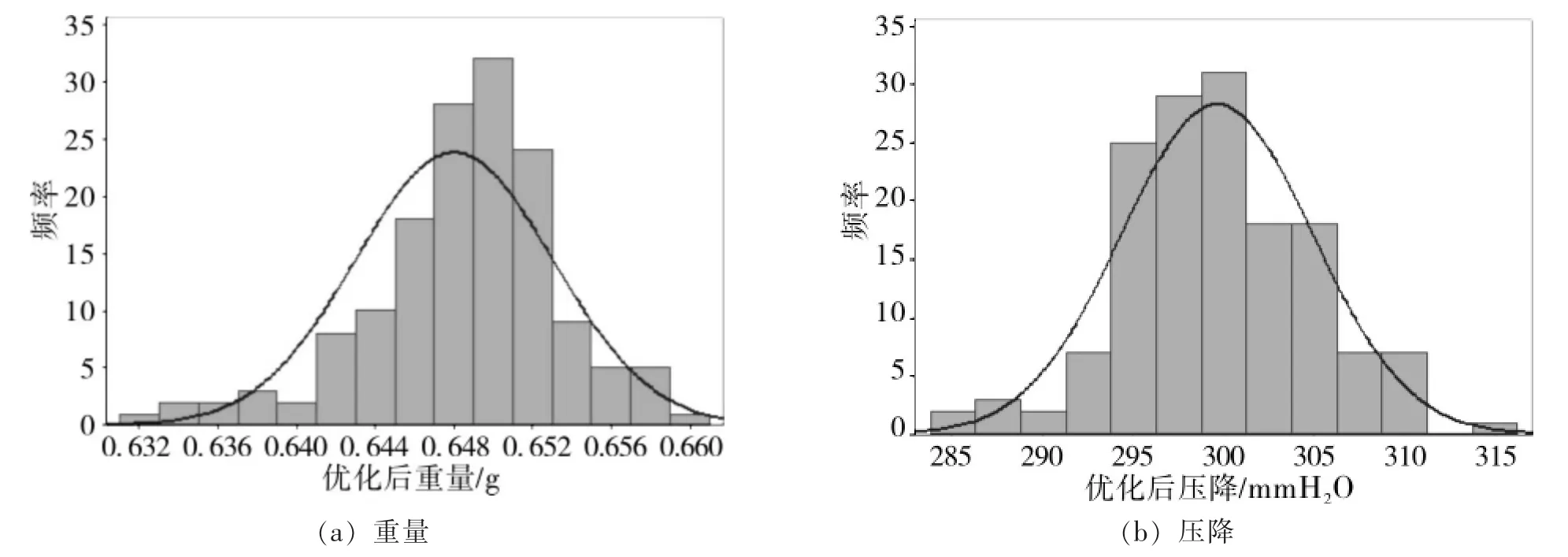
图7 优化后重量和压降的直方图 (包含正态分散曲线)

图8 优化后重量和压降的单直图
对成型机加工工艺参数进行调节后,依照前面的方法制棒150 支进行统计分析。 从图7优化后重量和压降的直方图可以明显的看出,重量相对与优化之前,中心值发生明显的右移,均值为0.648 g,与正常值0.65 g 十分接近,压降均值为300 mmH2O,未发生明显偏移。 通过图8 的单值图可以看出,重量和压降都向中心明显聚集,异常点的相对数量明显减少。

图9 优化前后重量和压降的单值控制图
将优化前后的重量、压降进行对比,如图9所示,也可以明显看出,优化后重量的均值与正常情况下的棒重接近,并且重量的波动性明显降低,稳定性发生了明显好转。 优化前后压降的均值几乎没有发生变化,但是可以看到优化后压降的稳定性明显改善。 压降STD 由优化前的10.85 降低至优化后的5.29。 滤棒质量得到大幅提升,质量改善的目的达到。
5 结论
(1)建立滤棒压降宏观模型,具体有:标准棒模型、横向分布不均模型、纵向分布不均模型。
(2)结合实际和理论,对模型的影响因素进行科学分析。
(3)利用一批质量波动较大的丝束进行制棒加工过程指导,压降STD 由优化前的10.85降低至优化后的5.29,质量改善效果显著。
(4)宏观模型能够精准快速的找出根本原因和解决之法,对生产具有一定指导意义。
