数学活动助力“空间观念”落地生根
2020-07-04张晓薇
摘 要:在小学数学图形与几何教学中,空间观念的培养对小学数学学习有着重要意义。空间观念的培养需要经历从抽象到想象的过程,在此过程中,往往需要借助一系列数学活动来帮助学生形成空间观念,本文以人教版小学数学三年级上册《周长的认识》实际教学为例,有序地开展数学活动,助力空间观念在课堂上落地生根。
关键词:数学活动 空间观念 周长
儿童认识事物的规律通常是直接感知——表象——抽象,他们的思维正处于从具象思维到抽象思维的过渡期,以具象思维为主,而空间观念是比较抽象的概念,所以让孩子建立空间观念是比较难的。因此,在实际教学中,教师要有针对性地设计一些数学活动,让学生经历和探究这些数学活动,从而获取和运用几何初步知识,并在运用过程中初步形成空间观念。
一、指一指——建立空间观念
在《周长的认识》这一课中,笔者设计了让学生指一指数学书封面的一周、课桌面的一周、纸巾盒面的一周、名片的一周等数学活动,让学生充分感知和理解物体表面和平面图形的“一周”,以此来帮助学生建立空间观念。
1.初步建立“一周”的概念
师:谁能来指一指数学书封面的边?
师:有一位同学他从这里开始,到这里结束了,他指的对吗?
生:不对,他没有指完。
师:如果要指完的话,应该怎么指?请你来指一指。我们一起来指一指。
师:我们从这个点开始,把它叫做起点,接着指,再回到起点,才是把它的边指全了。像这样,从起点再回到起点,正好指了它的一圈,在数学上,我们把“一圈”叫做“一周”。
从指数学书封面的边入手,在此过程中引导学生要按一定的顺序从起点出发再回到起点指一指,这样正好指了数学书封面的一圈,也就是数学书封面的一周,以此来揭示“一周”的概念,让学生对“一周”有了初步的认识。
2.逐步建立“一周”的概念
师:这是课桌的面,我們一起来指一指课桌面的边,请你上来指一指。
师:像这样,从起点再回到起点,就是课桌面的?
生齐:一周。
师:谁来指一指纸巾盒这个面的一周?这个面呢?
师:这是老师和同学们设计的名片,它们分别是我们熟悉的哪些图形?
生齐:正方形、三角形、圆形、心形。
师:这些图形的一周分别指的是什么呢?你能边指边说给你的同桌听吗?每人指两个。(教师把每个图形的一周取下来贴在黑板上)
在初识了数学书封面的一周的基础上,学生又经历了指一指各种物体表面和平面图形的一周,逐步建立起了物体表面和平面图形的“一周”的概念。教师把各种形状的名片的一周用线围起来,并把它们的一周取下来贴在了黑板上,将抽象的“一周”具象化,让学生对平面图形的“一周”有了直观的印象,从而帮助学生建立空间观念。
二、量一量——获得空间观念
空间观念是由长度、宽度、高度表现出来的客观事物在大脑中留下的概括的形象[1]。在学生建立了“一周”的概念的基础上,再让学生通过测量各种形状的名片一周的长度的数学活动来感知“一周”的长度,将抽象的“一周”变成具体有数值的长度,从而获得对周长概念的认识。
师:如果我要知道三角形的周长到底有多长,你有什么办法?
生1:可以用尺子量三角形每条边的长度,然后把三条边的长度加起来就是三角形的周长。
生2:可以用尺子量出黑板上这条线段的长度。
师:这条线段的长度指的就是?
生3:这条线段的长度指的就是三角形一周的长度。
师:三角形一周的长度就是?
生3:三角形一周的长度就是它的周长。
师:请你们同桌两人合作用第一种方法量一量、算一算三角形的周长,请一位小朋友上来量一量三角形一周的长度。(交流讨论)
师:要想知道这个圆形名片的周长,你有什么好办法?还能直接用尺子量吗?
生4:不能直接用尺子量,只要量黑板上那条线段的长度,就知道圆形名片的周长了。
师:这条线段的长度就是?
生4:这条线段的长度就是圆形一周的长度,也就是它的周长。
师:真是个好方法,请你们同桌两人合作来量一量。(交流讨论)
在量一量的数学活动中,让学生自己动手用两种方法测量三角形的周长,知道不仅可以通过测量并计算每条边的长度知道三角形的周长,还能借助细线把三角形的一周变成一条线段,只要测量出线段的长度就知道三角形的周长了。但是,要知道圆形这样的不规则图形的周长时,就不能直接用尺子来测量了,而是需要借助细线把圆形的一周变成一条线段,测量出线段的长度才能得到圆形的周长,在此环节中,渗透了化曲为直的思想,让学生对如何测量不规则图形有了初步的了解。在经历了测量规则图形和不规则图形的周长的数学活动之后,学生对周长有了一个量化的认识,进一步认识了周长的概念,进而获得了空间观念。
三、描一描——发展空间观念
空间观念的发展需要一系列的数学活动进行支撑,通过多种形式的探究活动充分调动学生的感官参与。在学生认识了物体表面和平面图形的周长的基础上,笔者设计了找图形的周长和描一描图形的周长这两个层次的数学活动,旨在让学生明确只有封闭图形才有周长,通过用眼观察、用脑思考和用手描,多感官参与,完善周长的概念。
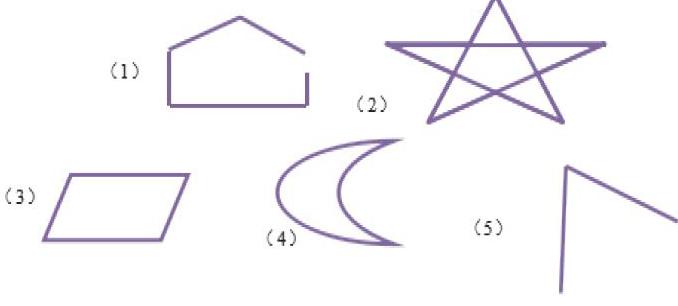
师:我们看这些图形,你能不能找到它们的周长呢? 哪些能?哪些不能?
生1:第一个和第五个图形不能找到它们的周长,其他的三个图形能找到它们的周长。
师:为什么第一个和第五个图形不能找到周长?
生1:因为它们有缺口。
师:像这样有缺口、不能从起点再回到起点的图形,我们把它们叫做不封闭图形,不封闭图形是没有周长的。剩下的这三个图形就叫做封闭图形,只有封闭图形才有周长。
师:现在请你们用彩笔描一描这三个图形的周长。
展台反馈:
师:老师看了一下,(3)和(4)你们描的都是一样的,而(2)描的不一样,(展台呈现错例和对例)你同意哪一个?你是怎么想的?
生2:我同意第二个,因为五角星的周长指的是最外面这一周的长度,不包括里面这些边。
师:请你能上来给大家指一指这个五角星的周长,我们一起来指一指。
师:看来五角星的周长不包括里面这些边(在错例上面把里面的边打上叉)请描错的小朋友用另一种颜色的笔再描一描它的周长,对的小朋友可以再指一指它的周长。
让学生判断图形是否有周长,在已有概念的基础上进一步理解周长概念的本质,知道只有封闭图形才有周长。在描一描图形周长的数学活动中,有五分之四的学生把五角星所有的边都描出来了,只有少数学生描了五角星外面的边。教师把学生的错例和对例在屏幕上对比呈现,把问题抛给学生,让他们仔细观察判断哪种描法是对的。这时,有一些原本描错的学生意识到了自己的问题,接着,教师请一个描对的孩子说一说他的想法,在他说完之后,又有一些孩子知道了自己的问题。于是,教师就让这个描对的孩子到上面来用手指一指这个五角星的周长,然后教师带着大家一起指一指五角星的周长,最后让错误的孩子用另一种颜色的彩笔再描一描五角星的周长。在此过程中,教师遵循由简单到复杂的过程,逐步引导孩子理解周长的概念,发展孩子的空间观念。
四、比一比——深化空间观念
在理解了周长概念的基础上,要重视知识的运用,加深对知识的理解,完善周长的空间形象,深化学生的空间观念。于是,在练习巩固的环节,笔者设计了不同层次的练习题,旨在让学生在比较图形的周长、辨析周长和面的数学活动中,内化周长的概念。
1.比——初步比较图形的周长
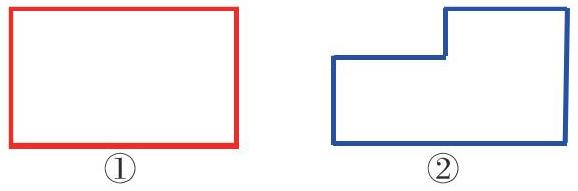
师:请你们比一比图①和图②这两个图形的周长。
师:谁来说说你是怎么比较这两个图形的周长的?
生1:我是用尺子量出了图形每一条边的长度,然后把每条边的长度加起来算出它们的周长。我算出来图①和图②的周长都是20厘米,所以它们两个的周长是一样长的。
师:还有别的方法吗?
生2:我是通过移动边的方法来比较的。把这条横着的边往上移,把这条竖着的边往下移,然后我发现这两个图形的周长是一样长的。
笔者设计的第一道练习题是比较长方形和一个变式图形的周长,让学生自主观察、思考,用多种方法来解决问题。在解决问题的过程中,让学生知道有时可以移动一些边,快速比较出图形的周长,体现了方法的优化性和解题的灵活性。
2.辨——深入比较图形的周长
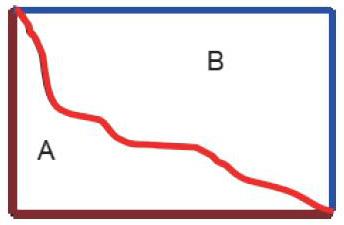
师:想一想,你有什么好的方法来比较A和B两部分的周长。
生1:因为A的这部分凹进去了,B的这部分突出来了,所以A的周长比B的周长短。
师:你们同意他说的吗?(有些学生表示同意,有些学生表示不同意,一些学生不确定。)
师:那请你们先用两种不同颜色的笔分别描一描A的周长、B的周长,描好了之后再来比较。
展台反馈(呈现错例和对例):
师:有这样两种不同的描法,你认为哪种是对的?你是怎么想的?
生2:我觉得第二种描法是对的,因为第一种描法少了中间这条边,这样就不能从起点再回到起点了。
师:那请描错的小朋友赶紧改一改,描好之后你们会发现什么?
生3:我发现A和B的周长是一样长的。因为长方形的对边相等,中间的这条边是A和B共有的,所以A和B的周长是一样的。
课件出示另外两个图形:
师:这两个图形中C和D的周长,E和F的周长,你能比较吗?
生4:C和D的周长是一样的,E和F的周长是一样的。因为长方形的对边相等,中间这条边是C和D共有的,所以C和D的周长是一樣的,同样地,E和F的周长也是一样的。
师:那中间这条边的位置还可以怎么放,也会让长方形的两部分的周长是一样的呢?这个问题留给同学们课后去思考。
在第一题的基础上,笔者设计了让学生初步辨析周长和面的数学活动,加深对周长的理解。第一位学生把看到的A和B的面当成了它们的周长,教师并没有明确指出他的错误,而是让学生用不同颜色的彩笔分别描出A和B的周长。可能是受前面描五角星周长的干扰,有一半的学生没有把中间的这条边描出来。此时,教师在展台上对比呈现错例和对例,让学生观察比较两种描法,有一部分学生意识到了自己的错误,这时请描对的学生来说一说,帮助描错的孩子认清自己的错误,然后再描一描,内化周长的概念。描好之后,学生会借助已有的认知,知道长方形的对边是相等的,从而发现A和B的周长是相等的。有了比较A和B的周长的经验,接下来,笔者设计了两个变式练习,让学生运用已有的知识经验来比较周长,深化了空间观念。最后,教师留了一个问题让学生课后思考,把空间观念的培养延伸到了课后。
空间观念不是单纯地几何概念教学,需要多种形式的数学活动来支撑。空间观念的培养不是一蹴而就的,需要长时间的经验积累。在平时的课堂教学中,教师要根据学生的年龄特点和认知发展规律,结合教材设计一些数学活动,并在数学活动中适时引导,助力空间观念在课堂上落地生根。
参考文献
[1]谢璐瑛.基于发展核心素养的小学数学空间观念培养思考——以人教版三上“长方形和正方形的周长”教学为例[J].新教师,2018(8):48-49.
作者简介
张晓薇(1993.5—),女,汉族,杭州余杭人,大学本科,现职称:二级教师,研究方向:小学数学。
