三自由度悬索并联机器人动态点对点轨迹跟踪控制

任凭 何梦伊

摘要：本文针对三自由度悬索并联机器人的动态点对点轨迹设计计算力矩控制器并进行跟踪控制。由于悬索并联机器人的悬索只能承受单向拉力，使得设计控制器时需考虑此张力约束，从而得到一组张力约束不等式以表示悬索张力和控制器参数间的关系。对不等式进行区间分析，从而确定满足悬索张力约束的控制器可靠参数空间。本文所提出的方法不仅可以实现对动态工作空间内的点对点轨迹的跟踪，而且当轨迹初始状态位于期望轨迹之外时，该方法可以实现运动轨迹的自动过渡。仿真结果表明，区间分析得到的控制器可靠参数空间可以确保末端执行器以指数速率收敛于期望轨迹，并始终保持悬索张力为正。

关键词：悬索并联机器人;计算力矩法;区间分析;轨迹跟踪

中图分类号：TP242 文献标识码：A

文章编号：1009-3044（2020）14-00014-06

并联机器人根据传递元件不同可以将并联机器人分为刚性连杆并联机器人和柔索牵引并联机器人（Cable-Driven Par-allel Robots，CDPRs）两类。柔索牵引并联机器人采用质量轻且无刚性的柔.1生绳索替代质量重的刚性连杆，使其既具有刚性连杆并联机器人刚度高、承载能力强等优点，又具有工作空间大、运动惯量小和运动速度快等优点。此外由于其结构简单、易于模块化，因此制造和維修成本较低。柔索牵引并联机器人的这些优势，使其在物料搬运、天文观测和运动仿真等领域得到了广泛运用。

为了提高机器人的性能，通常需要与控制方法相结合。根据控制时所选用模型的不同，通常将并联机器人的控制方法分为运动学模型控制和动力学模型控制两类。本文所选取的是动力学模型控制中的计算力矩方法，以机器人动力学模型为基础，加人位移、速度反馈和加速度前馈得到相应控制器，消除机器人系统中的一些非线性项，从而使机器人化为一个更容易受控制的线性定常系统嘲。

在对柔索牵引并联机器人的控制研究中，由于柔索只能对末端执行器产生拉力而不能产生推力，这种单向张力约束导致其控制研究具有一定难度。目前针对这种张力约束的处理方法主要存在以下三种：（1）经验法，根据仿真或实验结果反复试验控制器参数以满足柔索的张力约束。如Gorman等设计了三自由度悬索并联机器人的滑模控制器，并通过实验获得了控制器的增益数值。（2）张力分配优化方法，针对存在冗余索的柔索牵引并联机器人，通过优化算法将末端执行器的控制力分配至各条柔索，以维持柔索的张紧状态。如Khosravi等设计了平面三自由度四索构型的鲁棒PID控制器，采用零空间方法对张力进行了分配。（3）工作空间方法，对于不存在冗余索的悬索并联机器人，无法对张力分配进行优化，处理张力约束的方法可以与工作空间分析相融合。针对当前控制器参数推导其可达工作空间，在初始点位与目标点位之间设置过渡点位，使末端执行器分步到达期望位置。如Oh与Agrawal对六自由度悬索并联机器人控制器的参考输人进行规划，获得了位于控制器可达工作空间内的过渡点，并用解析不等式组描述出了满足张力约束的可达工作空间范围，从而使过渡点的计算更加高效。本文在上述方法的基础上，提出一种在悬索并联机器人控制研究中处理张力约束问题的新方法，即将对可达工作空间的分析转化为对控制器参数空间的分析。

目前针对三自由度悬索并联机器人的控制研究中，在国外，Jiang和Gosselin提出了一种点到点运动的动态轨迹规划方法，轨迹可以用来连接机器人静态工作空间以外的连续目标点，同时保证了每个目标点的零速度和加速度的连续性;在此基础上，Dion-Gauvin和Gosselin根据由初始点和最终点的加速度矢量定义的平面中的内摆线曲线，提出了一种新的点到点运动的动态轨迹规划方法，不仅满足上述条件，同时还可以通过适当选择内摆线的弧数保证柔索张力始终为正。而在国内，中国科技大学的张兵园等采用s型速度规划方法规划了工作空间内的矩形折面轨迹和平面圆形轨迹，并设计了一种实时张力补偿的自适应同步控制器对其进行轨迹跟踪控制。

本文同样以三自由度悬索并联机器人为研究对象，在文献规划的动态工作空间内点到点轨迹的基础上，设计轨迹跟踪计算力矩控制器，围绕柔索张力始终为正这一约束条件，得到满足此张力约束的控制器可靠参数空间，确保末端执行器收敛于给定轨迹，从而实现机器人的轨迹跟踪控制。

1机器人动力学模型

三自由度悬索并联机器人的几何构型如图1所示，由电机驱动的三个线轴分别固定在水平框架的p1、p2和p3位置，三条悬索分别从线轴伸出，连接至末端执行器。将该末端执行器视为质点m，质量忽略不计。图中柔索的长度分别用L1、L2和L3来表示。系统的静态工作空间可认为是线轴在水平框架上的三个固定点沿重力方向垂直向下构成的区域。

机构在运动过程中需时刻严格满足上述不等式，从而保证柔索的拉力始终大于零。因此在接下来的计算力矩控制器的设计中，不等式（4）、（5）和（6）将成为求解控制器参数的三个约束条件。

2计算力矩控制器设计

为了更好地对三自由度悬索并联机器人在动态工作空间内的动态点对点轨迹进行跟踪控制，首先采用文献中的方法设计计算力矩控制器。根据三自由度悬索并联机器人的动力学模型（1）和（2），柔索张力的控制输入可选为：

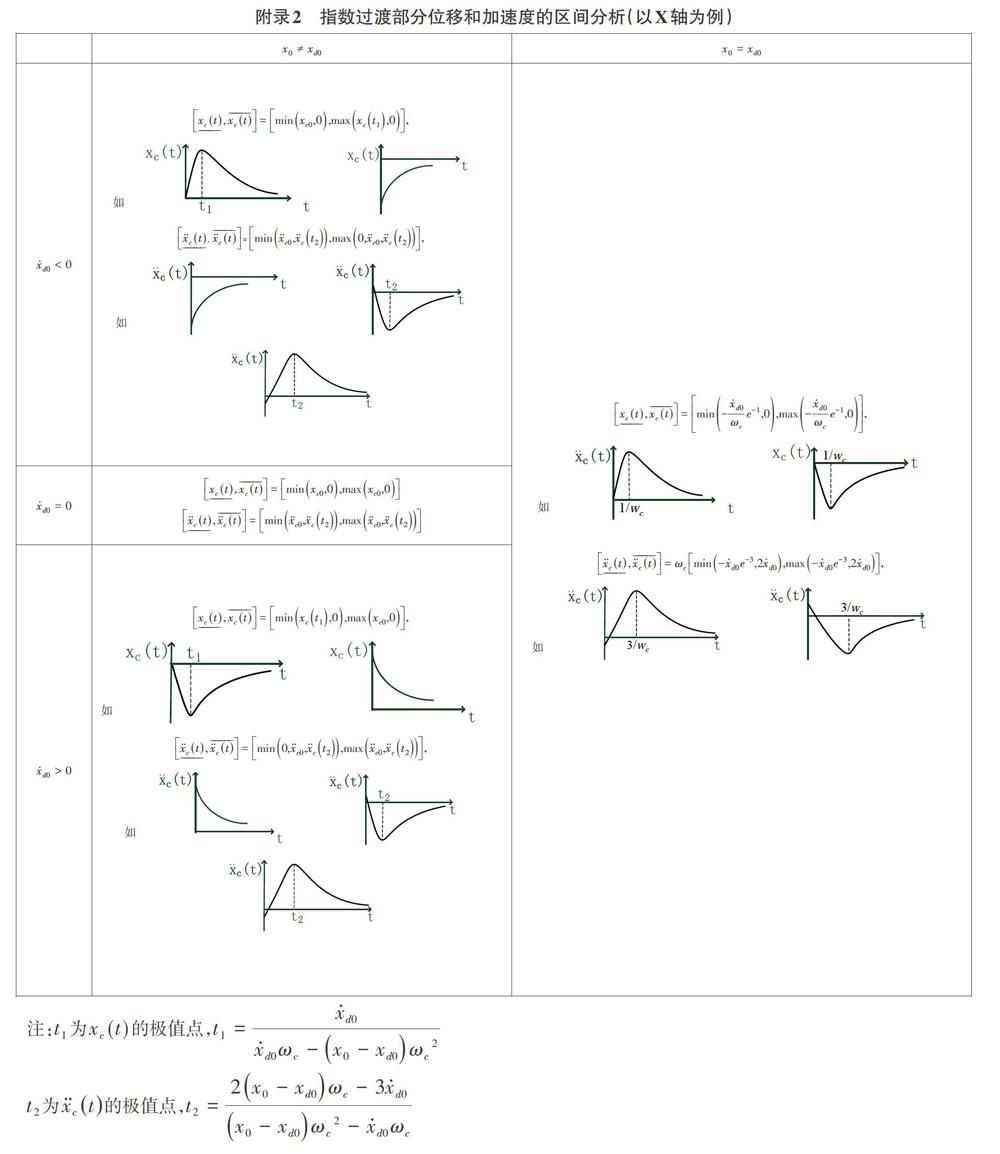
上述不等式为机构运动时张力约束条件区间分析的一般形式，通过求解不等式（18）（19）和（20）即可获得控制器参数满足张力约束的充分条件。其中，对指数过渡部分位移和加速度的区间分析如附录2所示。

3.2控制器参数可靠空间分析

动态点对点轨迹要求末端执行器依次通过静态工作空间外的一系列点位，因此采用分段连续方程构建期望运动轨迹。为了确保各目标点的瞬时速度均为零以及各段轨迹加速度的

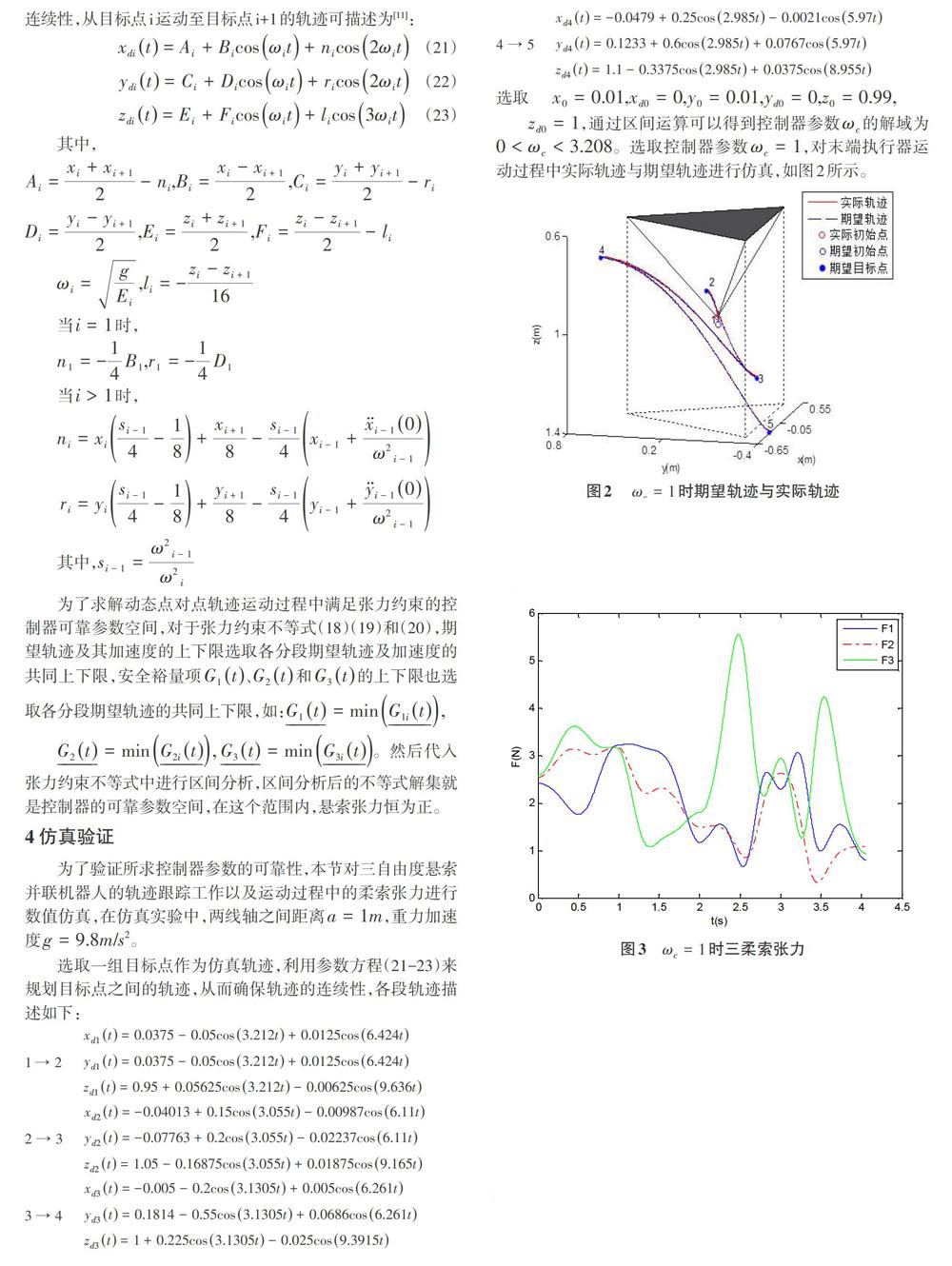
为了验证所求得的控制器可靠参数空间满足机构张力约束，对上述参数下的点对点运动过程中的张力进行仿真，如图3所示。从图3中可以看出机器人悬索在运动过程中张力恒为正。

5结论

本文针对三自由度悬索并联机器人的动态点对点轨迹进行跟踪控制，首先设计了一种计算力矩控制器，随后采用区间分析方法，围绕悬索并联机构的柔索张力始终为正这一约束条件得到三个不等式，从而获得控制器可靠参数空间。在此可靠参数空间内选择的控制器参数可严格保证三自由度悬索并联机器人在动态点对点轨迹运动过程中的三条悬索满足其张力约束。

仿真实验结果表明本文所提出的方法可以使末端执行器以指数速率收敛于期望轨迹，并实现运动轨迹的自动过渡。本文中采用控制算法与轨迹规划方法相互配合，可以提高动态响应速度，减少跟踪误差，从而提高悬索并联机器人的整体性能。这种控制方法不仅适用于三自由度悬索并联机器人中超出静态工作空间的动态点对点轨迹，而且可以扩展到六自由度构型的类似轨迹。