非牛顿流体充填料浆的管输摩擦阻力预测

杨晓炳 肖柏林 高谦

摘   要：在矿山充填采矿中，充填料浆在管道输送中的阻力损失计算是一重要环节. 为探索采用摩擦阻力系数模型简单高效地预测充填料浆管输阻力损失的方法，按照流态分类，总结了7种常用的非牛顿流体的摩擦阻力系数模型，结合一个具体案例分析讨论了模型的正确使用. 结果显示，选取模型时必须先考虑工程实际的流体类型和流态;对于最常见的宾汉塑性体的层流运动，使用Darby-Melson模型和Swamee-Aggarwal 方程可近似替代Buckingham-Reiner方程，其预测的沿程阻力损失与实际监测十分吻合，是宾汉塑性体层流流动首选的阻力预测模型，而Danish-Kumar模型则过低估计阻力值，适合赫德数较大的流体. 实际监测中的速度、沿程阻力波动原因与料浆配比的波动、骨料变异性、料浆非均匀性和充填采场倍线大小等因素密切相关且不可避免. 对于层流紊流过渡区流体的沿程阻力预测仍是工程难题.

关键词：非牛顿流体;膏体充填;高浓度充填;摩擦阻力系数;沿程阻力损失

Abstract：In mine backfilling， it is of great significance to calculate the slurry pressure loss in the pipeline transportation. In order to seek a simple and efficient method to predict the pressure loss through applying the friction factor correlations， this paper summarized seven friction factor correction models for non-Newtonian flow according to the flow state classication. After that， details on how to utilize the models to predict the pressure loss through a case study were presented. The results show that choosing a proper model is very important， where the practical flow type and conditions should be considered. For Bingham plastic laminar flow， the Darby-Melson and Swamee-Aggarwal model， which are approximations of the Buckingham-Reiner equation， are the first choices since their prediction results are in good agreement with the actual monitoring results of the pressure loss. However， the Danish-Kumar model underestimates the pressure drop and is suitable for flow with a large Hedstrom Number. Besides， monitoring fluctuations for the velocity and pressure loss in practice can be observed due to the slightly changeable slurry mixing proportion， the variability of the aggregate， the particle settling and mild segregation of the slurry during transportation， and the change of the stowing gradient. Finally， the pressure loss prediction for the transition flow region is still an engineering challenge.

Key words：Non-Newtonian flow;cemented paste backfill;high density backfill;friction factor;pressure loss

膠结充填采矿方法是地下矿山传统三大采矿方法之一，其利用胶凝材料、水和骨料在地表搅拌站搅拌均匀后，形成固体质量分数约60%～80%均匀料浆，利用重力自流或泵送，经管道输送到井下采场空区，经过一段时间的硬化后形成固态胶结充填体，提供支护功能，防止塌陷[1]. 胶结充填采矿法能有效解决选矿尾砂的地表堆存问题，保护环境，形成绿色循环经济[2];胶结充填采矿法具有最高的资源回收率，可有效管理地压，提高井下作业安全性[3];特别是当前浅地表资源的耗竭，采矿活动逐渐往深部发展，例如我国有越来越多的矿山开采达到并超过1 000 m[4-6]，深部开采意味着高温高应力，伴随着岩爆风险，此时胶结充填采矿法以其良好的地压管理能力，将成为深部开采的最主要采矿方法之一.

充填料浆可当作流态混凝土，必须能够实现自流平，也有人称之为低强度混凝土[7]. 研究如何将充填料浆安全、高效地输送到井下采场空区，是该技术成功应用的关键之一. 在工程实际中，充填料浆在管道输送中的沿程摩擦阻力计算，直接影响甚至决定了能否自流输送、充填系统的建设、设备（尤其是泵）选型、管网敷设形式等诸多核心问题. 国内外众多学者对摩擦阻力计算进行深入研究，如唐艳蓓等人[8]采用CFX软件进行数值模拟，分析流体在管道中的沿程阻力系数与管道内壁相对粗糙度的关系;于跃等人[9]以新阳煤矿为背景，提出了适用于该矿的高浓度胶结充填料浆的沿程阻力损失的理论公式;王石等人[10]研究了添加阴离子型聚丙烯酰胺（APAM）前后，全尾似膏体浆料管道输送的沿程阻力计算公式;吴爱祥等人[11]根据流体力学理论建立了考虑管壁滑移效应的膏体管道输送阻力模型，并根据响应面分析确定管道摩擦阻力的影响顺序由大到小依次为灰砂比、尾废比、浓度. 国内研究多直接提出用于针对特定某个矿山的阻力计算的经验公式，著名的沿程阻力计算公式还有如金川公式、长沙矿冶院研究公式、鞍山黑色金属矿山设计院公式[12]，然而这些公式应用复杂，往往是经验公式且仅适用于某一特定情况，很少对前提进行界定，缺乏通用性总结;而国外研究多采用无量纲的摩擦阻力系数的概念，并通过Darcy-Weisbach方程转化为具体沿程阻力值[13].

在国内矿山实际中，也有很多采用设计环管实验的方法，直接对阻力进行准确测量[14-15]. 环管实验是最准确的测试方法，但其代价极其昂贵，实验过程及操作繁杂费事[16]，在实际中经常需要对料浆进行不断调整，采用环管实验是极其浪费的一种做法. 最有效的办法是采用阻力计算公式进行预测，然而在国内众多文献中，并没有多少正确利用阻力系数预测充填料浆阻力的案例. 其原因之一是公式的数量繁多，另一个是缺乏考虑料浆流态、状态的多变性，从而选择正确、适用所需情况下的阻力计算方法. 因此本文在总结国内外常用关键的一些宾汉塑性体的摩擦阻力系数计算方法的基础上，解释说明各方法的适用条件，然后结合一个具体案例，探讨如何正确应用这些公式进行充填料浆摩擦阻力预测，并对这些公式的适用性进行评价. 希望能为正确使用这些模型提供参考.

1   宾汉塑性体的摩擦阻力系数计算模型

在工程实际中，现代充填料浆基本可分为高浓度及膏体两种，表现为非牛顿体特性，且绝大多数是宾汉塑性流体[17]. 宾汉塑性体料浆同其他流体类似，在管道中流动同样可以分为层流运动、紊流运动及过渡区三种流态，对于过渡区，有太多不确定性，仍是当前的学术难题，因此本节首先按流态分，总结了适用于层流区、紊流区及层流紊流通用的摩擦阻力系数计算方法.

1.1   适用层流区的摩擦阻力系数模型

1.1.1   Buckingham-Reiner方程

Buckingham-Reiner方程[18]适用于宾汉塑性体层流状态下的摩擦阻力系数计算模型，如式（1）所示. 可见该方程为fL的四阶隐式方程，虽然可以获得精确解析解，但其计算过程复杂，有诸多研究者寻找该方程的显式近似解.

1.1.2   Darby-Melson模型

1.1.3   Swamee-Aggarwal 方程

Swamee-Aggarwal 方程[20]用来直接求解宾汉塑性体层流下的Darcy-Weisbach摩擦阻力系数fL，它是Buckingham-Reiner隐式方程的一种近似，如式（5）所示.

1.2   适用紊流区的摩擦阻力系数模型

1.2.1   Colebrook-White方程

该模型[21]是一个仅适用于紊流区的通用模型，除了宾汉塑性体，也可用于其他如H-B等流体，该模型认为，假如相对粗糙度的影响甚微，可用式（6）的隐式方程求解水力光滑管的摩擦阻力系数.

1.2.2   Wilson-Thomas模型

该模型[22]适用于宾汉塑性体料浆的紊流运动阻力系数计算：

1.2.3   Dodge-Metzner模型

该模型[23]修正了剪切变稀的紊流运动非牛顿体在水力光滑管的摩擦阻力系数：

1.3   适用层流紊流的通用模型

Danish等人[24]通过采用阿多米安分解法提出了计算层流下的摩擦阻力系数计算方法，如式（12）所示.

2   充填料浆沿程阻力预测的工程案例应用及评价

前面总结了7种常用的摩擦阻力系数模型，下面结合一个具体案例讨论这些模型的应用，并进行评价.

2.1   利用模型預测沿程阻力的步骤

上述模型中有的适用于层流运动，有的适用于紊流运动，在具体实际应用时必须事先判断充填料浆在管道中的流态，即计算其雷诺数. 从式（1）中雷诺数的定义可知，工程中某一流体的雷诺数与料浆的动力黏度、料浆密度、料浆流速以及管道直径有关;密度、流速及管道直径可以根据具体矿山实际情况获取，动力黏度是料浆流变参数之一，需要通过流变仪进行测量. 通过流变仪还可以测量另一个流变参数——屈服应力，这两个流变参数也是计算赫德数的必要条件之一.

利用摩擦阻力系数模型预测充填料浆的沿程阻力损失的步骤是： 1）用流变仪测量料浆的动力黏度及屈服应力; 2）得到的料浆流变参数结合工程实际的管道大小、料浆密度及流速，计算得到料浆雷诺数及赫德数; 3）根据得到的雷诺数判断料浆在管道中的流态，结合赫德数，正确选取一个摩擦阻力系数模型;4）根据模型计算对应的摩擦阻力系数，通过Darcy-Weisbach方程转换成沿程水头损失hf，如式（14）所示.

2.2   应用案例

2.2.1   工程背景

金川镍矿位于中国甘肃省，是中国最大的镍钴生产基地. 龙首矿是金川三个矿山之一，其采用下向进路式分层充填，高浓度料浆通过自流管输到采场，充填倍线3 ～ 4，采用水泥为胶结剂，添加量为280～310 kg/m3，骨料为棒磨砂和废石混合骨料（最大粒径5 mm，D50 = 1～2 mm，棒磨砂废石比例为7 ∶ 3），料浆质量分数为78%. 工程中遇到的问题是，料浆分层离析较严重，对管道磨损及井下充填体稳定性影响很大，其主要原因是缺少-20 μm细颗粒含量，通过实验对料浆进行优化后，最终优化后的料浆配比是：水泥掺量300 kg/m3，料浆质量分数为78%，采用石灰石粉替换部分原混合骨料，以增加细颗粒含量，替换量为骨料质量的10%.

2.2.2   实验材料

该案例中所用的材料均为龙首矿充填系统实际生产中所用的材料，其中水泥为当地金昌金泥集团的42.5水泥，骨料为棒磨砂（A1）、废石（A2）混合骨料，添加的细骨料为石灰石粉（A3），这些骨料的粒径级配分布如图1所示. 骨料的主要化学成分如表1所示.

2.2.3   调整后的料浆流变特性测试

按照上述步骤，首先对调整后的料浆在实验室内进行流变测试，料浆配比为水泥掺量300 kg/m3，固体质量分数为78%，骨料中混合骨料与石灰石粉的比例为9 ∶ 1，混合骨料中棒磨砂与废石的比例为7 ∶ 3，料浆密度ρm = 2 007.2 kg/m3.

采用Brookfiled 的R/S-SST流变仪+Rheo3000软件对料浆在室温环境下进行流变测试. 测试前将混合物用搅拌机搅拌5 min至均匀状态，然后装入600 mL的玻璃烧杯中，立即开始流变测试，流变仪采用VT-40-20叶片转子，测试时采用控制剪切速率模式（CSR），为了减少通道效应及蠕变效应，测试时先用120 s-1的速率剪切2 min，然后设置剪切速率从120 s-1在120 s内逐渐降低至0 s-1得到，该期间记录的剪切速率与剪切应力关系如图2所示，并用宾汉塑性体模型进行拟合，得到的结果为：

2.2.4   计算雷诺数选择合适的模型

龙首矿西部充填站的充填管道直径D = 0.11 m，调整后料浆的密度ρm = 2 007.2 kg/m3，西部充填站运行中控制系统终端监测得到的流量除以管道截面积可以换算成料浆流动速度（见图3）;把已知参数代入式（1）雷诺数的计算公式，可以得到雷诺数的变动范围，如图3所示.

由图3可知，该条件下料浆在管道中大部分时间处于层流运动（雷诺数小于2 100），但也有一小部分由流速变化导致其处于层流紊流过渡区. 引起料浆流速变化波动的原因有3个：1）充填系统配比波动，如料浆质量分数为78%，但实际中不可能完全稳定在78%，一般在77%～79%间波动，这是充填系统本身特性所决定，是不可避免的;2）充填材料，尤其是骨料的差异性，搅拌桶中虽然是连续搅拌，但在不同时刻放入的骨料具有差异性，其粒径级配不可能完全一样，这将引起料浆密度、黏度、屈服应力等各个特性的波动，从而造成流速波动;3）充填料浆的非均质性，高浓度料浆可以当作似均质流，但达不到理想均质状态，因此料浆在管道纵截面上的速度会有细微差异，再加上金川充填料浆中骨料颗粒的最大粒径达12 mm，料浆中大颗粒的不规则运动恰好经过管道传感器位置将可能引起波动异常.

因此，可以把该料浆当作是层流运动，根据第1节所总结的模型，该情况下可选用的模型有Buckingham-Reiner方程、Darby-Melson模型、Swamee-Aggarwal 方程和Danish-Kumar模型;其中Swamee-Aggarwal 方程只是Buckingham-Reiner高阶隐式方程的显式近似求解，因此两个方程的解差异不大，为了简化计算，采用Swamee-Aggarwal 方程，即最终采用式（4）、式（5）和式（12）3种模型进行预测.

3   结果验证与评价

3.1   验证实验

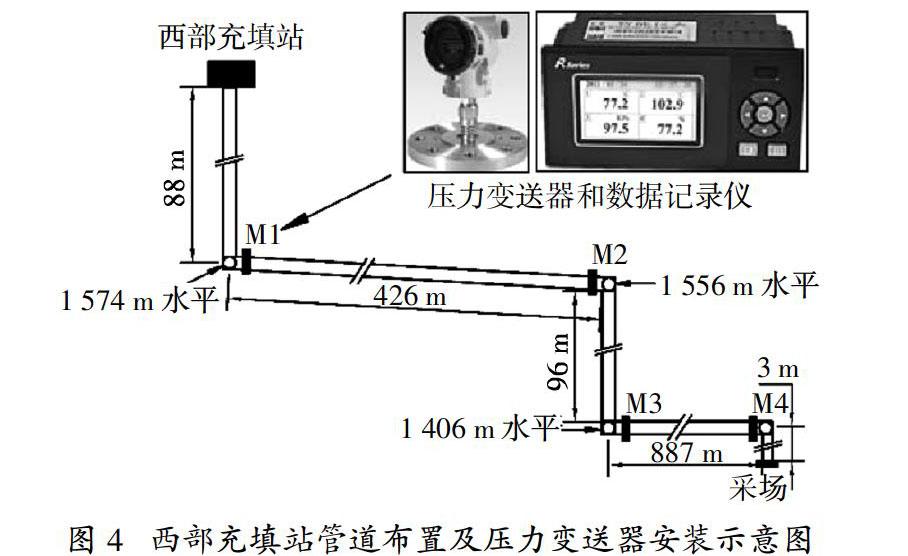
为了验证及评价所选方法所预测沿程阻力损失的准确性和适用性，在龙首矿西部充填站已有的充填管道系统架设压力传感器，通过实际工业实验验证模型的适用性与准确性. 西部充填站的充填管网水平管总长为1 520 m;垂直管总长为421 m，充填倍线3.61，管道内径110 mm;共安装了4个压力变送器以监测料浆在管道流动中的阻力变化，并采用无纸记录仪每隔1 min记录一次监测点的压力. 管网简图、监测点的位置及安装如图4所示.

3.2   结果分析与评价

以调整后的料浆配比进行工业实验，所有流量流速、压力、浓度等监测信息都传输至地表控制终端，根据监测点的流速等相关数据代入模型，可以计算得到各模型的预测摩擦阻力系数，再经过式（15）即可转换成对应预测的沿程阻力损失;实际监测中将两个不同监测站监测的压力差除以该两个监测站的距离即为实际监测沿程阻力损失;最终采用的3种模型沿程阻力预测结果与监测点所记录的实际阻力损失对比如图5所示. 从图5中可以得到：

1）首先对于实际监测得到的压力损失，其波动较大，原因除了在2.2.4所述的配比波动、骨料变异性及料浆非均匀性以外，还与实际系统运行状态和充填采场倍线大小等关系密切相关，在工业中这种波动是正常及不可避免的.

2）Swamee-Aggarwal方法及Darby-Melson方法预测得到的沿程阻力几乎重合，前者略大于后者，这是因为这两个方程的本质都是Buckingham-Reiner，只是进行显式求解的不同造成了略微不同. 但两者预测到的沿程阻力与实际监测的沿程阻力基本一致，处于同一水平波动，吻合良好;而与实际监测差异较大的部分点是由于流态变化造成的. 由前文所述速度及雷诺数波动中，已经验证有极少时刻，料浆处于层流紊流过渡区，此时沿程阻力将十分不可控，变化较大，而这里的这两种方法都是适用层流运动下的阻力计算，因此造成这些部分预测值与实测值差异较大. 从工程实际上看，Swamee-Aggarwal方法及Darby-Melson模型能预测得到与实际工业充填中相吻合的阻力损失.

3）Danish-Kumar模型预测得到的沿程阻力损失与实际相差较大，其预测值远小于实测值，且对速度波动的反应也不明显，“失真”较严重. 在计算过程中发现中间参数K2十分微小，达到10-10，本文认为其比较适用赫德数He较大的流体（50 000以上），但考虑篇幅问题并未进行深入解释.

4   结   论

本文通過总结文献常用的7个非牛顿流体的摩擦阻力系数计算模型，按照其适用流态类型进行分类并简要介绍讨论了具体用法，然后结合一个具体案例论述了模型的具体应用，得到了以下几点结论：

1）高浓度或膏体充填料浆可以看作均质或似均质的非牛顿体，可以通过选择正确的模型计算其在工程实际管道流动中的沿程阻力损失;正确模型的选择十分重要，必须先考虑工程实际流体的类型（幂次、宾汉体、H-B体）、流态（雷诺数），才能根据这些前提选择准确的阻力系数模型.

2）对于宾汉塑性体的层流运动，Buckingham-Reiner方程、Darby-Melson模型、Swamee-Aggarwal 方程和Danish-Kumar模型是4种最常用的预测模型，其中Buckingham-Reiner方法是4次隐式方程，必须通过迭代才能求解，实际中往往用Darby-Melson模型和Swamee-Aggarwal 方程进行近似替代;通过实验验证，Darby-Melson和Swamee-Aggarwal方法所预测的沿程阻力与实际监测十分吻合，处于同一平均位置波动，是宾汉塑性体层流运动首选的阻力预测模型，而Danish-Kumar模型则过低估计阻力值，适合赫德数较大的流体.

3）实际中速度、沿程阻力波动的原因与料浆配比波动、骨料变异性、料浆非均匀性、实际系统运行状态和充填采场倍线大小等因素密切相关，是不可避免的;尽管如此，Darby-Melson和Swamee-Aggarwal方法也能根据速度波动模拟其阻力的变化，而当料浆进入层流紊流过渡区时则误差较大，对于大部分时刻处于过渡区或紊流区的流体必须采用其他模型进行预测.

参考文献

[1]    刘浪，辛杰，张波，等. 矿山功能性充填基础理论与应用探索[J]. 煤炭学报，2018，43（7）：1811—1820.

LIU L，XIN J，ZHANG B，et al. Basic theories and applied exploration of functional backfill in mines[J]. Journal of China Coal Society，2018，43（7）：1811—1820. （In Chinese）

[2]    白腾飞，宋瑞卓. 现代矿山充填采矿法浅析[J]. 世界有色金属，2018，499（7）：55—57.

BAI T F，SONG R Z. Analysis of modern mine filling mining method[J]. World Nonferrous Metal，2018，499（7）：55—57. （In Chinese）

[3]    高谦，杨晓炳，温震江，等. 基于RSM-BBD的混合骨料充填料浆配比优化[J]. 湖南大学学报（自然科学版）， 2019， 46（6）：47—55.

GAO Q，YANG X B，WEN Z J，et al. Optimization of proportioning of mixed aggregate filling slurry based on BBD response surface method[J]. Journal of Hunan University （Natural Sciences），2019，46（6）：47—55.（In Chinese）

[4]    康红普，王国法，姜鹏飞，等. 煤矿千米深井围岩控制及智能开采技术构想[J]. 煤炭学报，2018，43（7）：1789—1800.

KANG H P，WANG G F，JIANG P F，et al. Conception for strata control and intelligent mining technology in deep coal mines with depth more than 1 000 m[J]. Journal of China Coal Society，2018，43（7）：1789—1800. （In Chinese）

[5]    程桦，彭世龙，荣传新，等. 千米深井L型钻孔预注浆加固硐室围岩数值模拟及工程应用[J]. 岩土力学，2018，39（S2）：281—291.

CHENG H，PENG S L，RONG C X，et al. Numerical simulation and engineering application of grouting reinforcement for surrounding rocks of chamber in deep of 1 000 m by L-shaped boreholes[J]. Rock and Soil Mechanics，2018，39（S2）：281—291. （In Chinese）

[6]    江飛飞，周辉，刘畅，等. 地下金属矿山岩爆研究进展及其预测与防治[J]. 岩石力学与工程学报，2019，38（5）：956—972.

JIANG F F，ZHOU H，LIU C，et al. Progress prediction and prevention of rock bursts in underground metal mines[J]. Chinese Journal of Rock Mechanics and Engineering，2019，38（5）：956—972. （In Chinese）

[7]    宋少民，闫少杰，刘小端. 铁尾矿微粉对大流态混凝土性能的影响研究[J]. 混凝土，2017（11）：77—80.

SONG S M，YAN S J，LIU X D. Influence of iron ore tailings powder on the performance of high fluidity concrete[J]. Concrete，2017（11）：77—80. （In Chinese）

[8]    康艳蓓，张浩，许岩. 粗糙度对幂律流体湍流沿程阻力系数的影响[J]. 煤气与热力，2018，38（8）：49—54.

KANG Y B，ZHANG H，XU Y. Influence of roughness on drag coefficient along path of power-law fluid turbulence[J]. Gas & Heat，2018，38（8）：49—54. （In Chinese）

[9]    于跃，郑伟钰，程坤，等. 煤矿高浓度胶结充填料浆管道沿程阻力研究[J]. 煤矿安全，2017，48（2）：72—75.

YU Y，ZHENG W Y，CHENG K，et al. Research on pipe flow resistance loss of high concentration filling materials in coal mine[J]. Safety in Coal Mines，2017，48（2）：72—75. （In Chinese）

[10]  王石，张钦礼，王新民，等. APAM对全尾似膏体及其管道输送流变特性的影响[J]. 中南大学学报（自然科学版），2017，48（12）：3271—3277.

WANG S，ZHAN Q L，WANG X M，et al. Influence of APAM on rheological properties of unclassified tailings paste-like and its pipeline transportation[J]. Journal of Central South University（Science and Technology），2017，48（12）：3271—3277. （In Chinese）

[11]  吴爱祥，程海勇，王贻明，等. 考虑管壁滑移效应膏体管道的输送阻力特性[J]. 中国有色金属学报，2016，26（1）：180—187.

WU A X，CHENG H Y，WANG Y M，et al. Transport resistance characteristic of paste pipeline considering effect of wall slip[J]. The Chinese Journal of Nonferrous Metals，2016，26（1）：180—187. （In Chinese）

[12]  蔡嗣经，王洪江. 现代充填理论与技术[M]. 北京：冶金工业出版社，2012：67—69.

CAI S J，WANG H J. Theory and technology of modern filling[M]. Beijing：Metallurgical Industry Press，2012：67—69. （In Chinese）

[13]  ASSEFA K M，KAUSHAL D R. A comparative study of friction factor correlations for high concentrate slurry flow in smooth pipes[J]. Journal of Hydrology and Hydromechanics，2015，63（1）：13—20.

[14]  邵亚平，郭利杰，陈寅，等. 基于环管试验确定粗骨料膏体充填料浆管道输送参数[J]. 有色金属（矿山部分），2018，70（4）：20—23.

SHAO Y P，GUO L J，CHEN Y，et al. Determination of conveying parameters of coarse aggregate paste filling slurry pipeline based on annular tube test[J]. Nonferrous Metals （Mine Section），2018，70（4）：20—23. （In Chinese）

[15]  刘冰，李夕兵. 全磷废料高浓度充填两相流环管试验研究[J]. 黄金科学技术，2018，26（5）：615—621.

LIU B，LI X B. Study on two-phase flow loop test of high concentration backfill with total phosphorus waste[J]. Gold Science and Technology，2018，26（5）：615—621. （In Chinese）

[16]  BHARATHAN B，MCGUINNESS M，KUHAR S，et al. Pressure loss and friction factor in non-Newtonian mine paste backfill：modelling，loop test and mine field data[J]. Powder Technology，2019，344：443—453.

[17]  苗苗，雪凱旺，苗芳，等. 石灰石粉对水泥浆体水化特性及流变性能的影响[J]. 湖南大学学报（自然科学版），2018，45（12）：90—96.

MIAO M，XUE K W，MIAO F，et al. Influence of limestone powder on hydration characteristics and rheological properties of cement paste[J]. Journal of Hunan University （Natural Sciences），2018，45（12）：90—96.（In Chinese）

[18]  REES D A，BASSOM A P. The effect of internal and external heating on the free convective flow of a Bingham fluid in a vertical porous channel[J]. Fluids，2019，4（2）：95.

[19]  KUMAR S. Determination of pressure drop characteristics of fly ash suspension with additive for hydraulic transportation[J]. Journal of Applied Fluid Mechanics，2018，11（5）：1387—1393.

[20]  F?REDER K，SVARDAL K，KRAMPE J，et al. Rheology and friction loss of raw and digested sewage sludge with high TSS concentrations：a case study[J]. Water Science and Technology，2018，2017（1）：276—286.

[21]  AZIZI N，HOMAYOON R，HOJJATI M R. Predicting the Colebrook-White friction factor in the pipe flow by new explicit correlations[J]. Journal of Fluids Engineering，2019，141（5）：051201.

[22]  ADANE K F，AGELIN C M. Laminar-turbulent transition flows of non-Newtonian slurries：models assessment[J]. Journal of Fluids Engineering，2019，141（1）：011104.

[23]  ANBARLOOEI H R，CRUZ D O，RAMOS F，et al. On the connection between Kolmogorov microscales and friction in pipe flows of viscoplastic fluids[J]. Physica D：Nonlinear Phenomena，2018，376：69—77.

[24]  DANISH M，KUMAR S. Approximate explicit analytical expressions of friction factor for flow of Bingham fluids in smooth pipes using Adomian Decomposition Method[J]. Communications in Nonlinear Science and Numerical Simulation，2011，16（1）：239—251.